Seely F.B. Analytical Mechanics for Engineers
Подождите немного. Документ загружается.

CORIOLIS' LAW
271
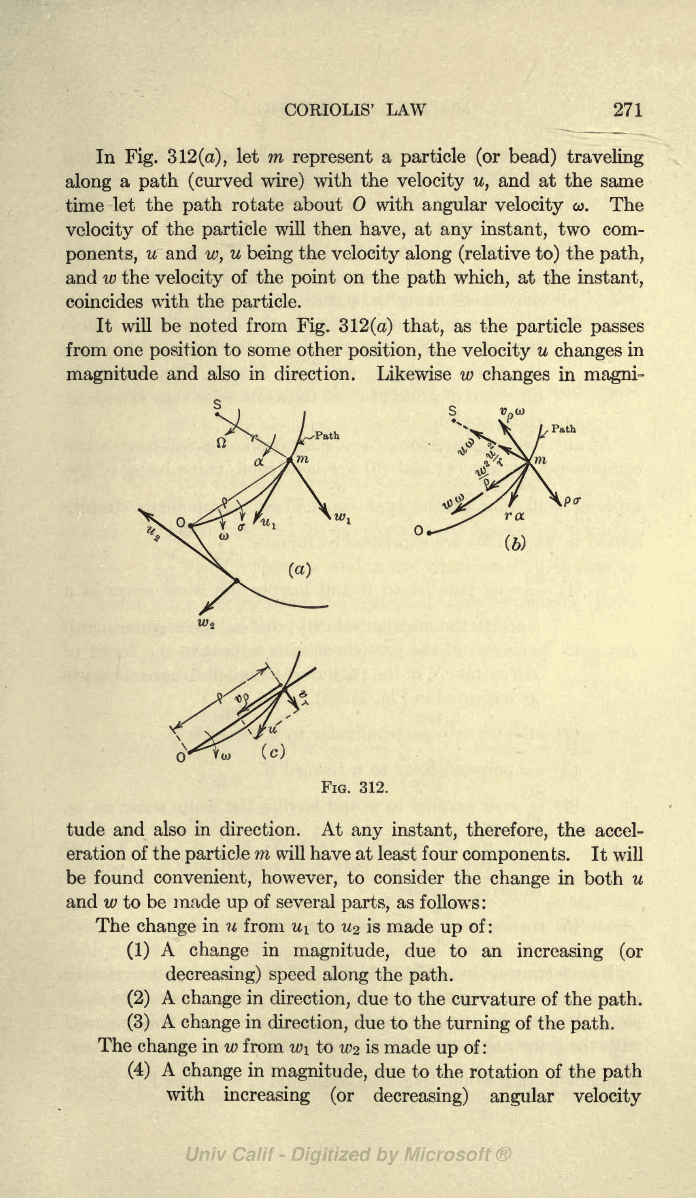
In
Fig.
3
12
(a),
let
m
represent
a
particle (or
bead)
traveling
along
a
path
(curved
wire)
with the
velocity
u,
and
at the same
time
let
the
path
rotate about with
angular
velocity
o>. The
velocity
of
the
particle
will
then
have,
at
any instant,
two com-
ponents,
u and
w,
u
being
the
velocity
along
(relative to)
the
path,
and
w the
velocity
of the
point
on the
path
which,
at
the
instant,
coincides
with
the
particle.
It will be noted
from
Fig.
3 12
(a)
that,
as the
particle passes
from one
position
to some other
position,
the
velocity
u
changes
in
magnitude
and also
in
direction. Likewise w
changes
in
magni-
Path
(c)
FIG. 312.
tude
and also
in
direction.
At
any instant,
therefore,
the
accel-
eration of
the
particle
m
will
have
at
least four
components.
It
will
be
found
convenient, however,
to consider
the
change
in
both u
and w
to be
made
up
of
several
parts,
as
follows:
The
change
in
u
from
u\
to
u^
is
made
up
of:
(1)
A
change
in
magnitude,
due to an
increasing (or
decreasing)
speed
along
the
path.
(2)
A
change
in
direction,
due
to
the
curvature of the
path.
(3)
A
change
in
direction,
due to the
turning
of
the
path.
The
change
in
w from
w\
to
W2
is made
up
of :
(4)
A
change
in
magnitude,
due
to the
rotation of
the
path
with
increasing (or
decreasing) angular
velocity

272
MOTION
OF A
PARTICLE
(assuming
p
to remain
constant,
that
is,
considering
the
particle
to
be fixed
to the
path).
(5)
A
change
in
direction,
due
to the
rotation of the
path
(considering
the
particle
fixed to the
path)
.
(6)
A
change
in
magnitude,
due to the
change
in
length
of
p
(assuming
co
to remain
constant),
caused
by
the
movement
along
the
path.
(7)
A
change
in
direction,
due to the
change
in the direc-
tion
of
p,
caused
by
the
motion
of the
particle along
the
path (assuming
the
path
fixed).
The
change
in
direction of
p
and
of w
are
the
same
since
they
remain at
right
angles.
At
any
instant,
therefore,
the
acceleration of
m
will
have seven
components,
unless
(4)
and
(6)
are
combined,
three
being
of the
type
,-
and
four of the
type
vu.
These
components (repre-
ctt
sented
in
Fig.
3126)
are
expressed
as
follows:
(1)
-r-
=
ra
parallel
to
u
and
having
the
same sense
as
u
since
12,
the
angular
velocity,
and
a,
the
angular
accel-
eration,
of
the
particle
m
with
respect
to the
center of
curvature,
S,
of the
path
were assumed to
agree
in
sense
as
indicated
in
Fig. 312(a).
u
2
(2)
wfl
=
12
2
r
=
perpendicular
to
u
}
towards
S.
(3)
wco
perpendicular
to
u
toward S.
(4)
-rr
=
per
parallel
to w and
having
the same
sense
as
w,
CLL
since
co,
the
angular velocity,
and
a,
the
angular
acceleration,
of the
path
with
respect
to are
assumed
to
agree
in
sense.
w
2
(5)
wu
=
u>
2
p
=
perpendicular
to
w,
toward
0.
By
referring
again
to
Fig.
312(a),
it will
be noted that the
velocity
u
could
also
be
produced
by allowing
the
particle
(bead)
to
slide
along
the
straight
line
p
as the line
p
is rotated about the
center
with
the
same
angular velocity,
co,
as that of
the
path.
The
two
components
of
u would then
be
V
T
=
cop
and
V
P
=
~JT
(
see
Fig.
312c).
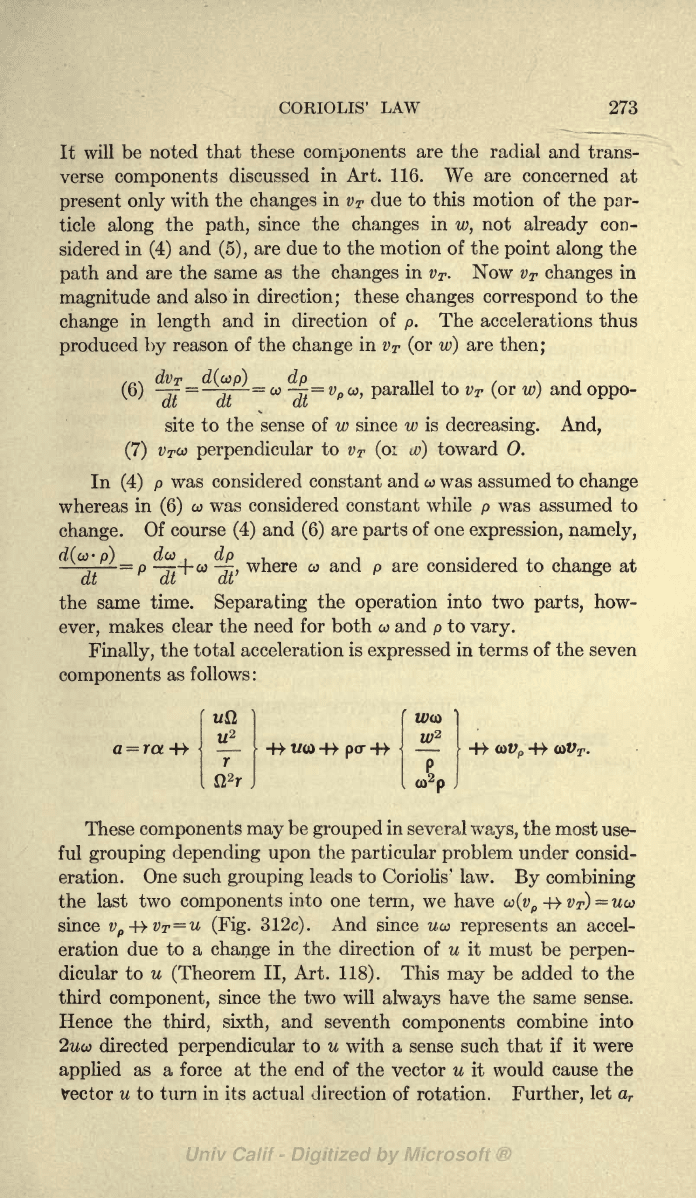
CORIOLIS' LAW
273
It
will
be noted
that these
components
are the radial
and
trans-
verse
components
discussed
in Art.
116. We
are
concerned
at
present only
with
the
changes
in V
T
due to this
motion of
the
par-
ticle
along
the
path,
since
the
changes
in
w,
not
already
con-
sidered
in
(4)
and
(5),
are due to
the
motion of
the
point
along
the
path
and are the same
as the
changes
in V
T
.
Now
V
T
changes
in
magnitude
and
also
in
direction;
these
changes correspond
to
the
change
in
length
arid in direction
of
p.
The accelerations
thus
produced
by
reason of
the
change
in
V
T
(or
w)
are
then;
,_ x
dv
T
(6)
77
dp
,
>.
u
~~T
f
=
V
P
<*> parallel
to
V
T
(or
w)
and
oppo-
Cut
And,
j
t
Clt
at
site to
the sense of
w since w is
decreasing.
(7)
V
T
U
perpendicular
to
V
T
(01
w)
toward 0.
In
(4)
p
was
considered
constant
and o>
was assumed
to
change
whereas
in
(6)
co was
considered constant while
p
was assumed to
change.
Of course
(4)
and
(6)
are
parts
of one
expression,
namely,
,'
-P
-s+w-si
where
co and
p
are
considered to
change
at
at
at
at
the same
time.
Separating
the
operation
into two
parts,
how-
ever,
makes
clear the need
for
both
co and
p
to
vary.
Finally,
the total acceleration
is
expressed
in
terms of the seven
components
as
follows :
po-
+>
100
w
2
These
components may
be
grouped
in
several
ways,
the
most
use-
ful
grouping
depending
upon
the
particular
problem
under
consid-
eration.
One
such
grouping
leads to
Coriolis
1
law.
By
combining
the
last
two
components
into one
term,
we have
w(v
p
-&V
T
}=UU
since
v
p
-ftvT
=
u
(Fig.
312c).
And
since
wco
represents
an
accel-
eration
due to a
change
in the
direction of
u
it
must
be
perpen-
dicular
to
u
(Theorem
II,
Art.
118).
This
may
be added
to
the
third
component,
since
the
two will
always
have the
same sense.
Hence
the
third,
sixth,
and
seventh
components
combine into
2wco
directed
perpendicular
to
u
with
a sense such
that if
it were
applied
as
a force
at the end
of
the vector
u it
would
cause the
Vector
u to turn in
its actual direction
of rotation.
Further,
let
a
r

274
MOTION
OF A PARTICLE
represent
the
vector sum
of
the first
two
components
and
let
a
m
represent
the
vector
sum of
the fourth and
fifth,
that
is,
let
O
*>
Or-
a
m
-pff
>y.
The total
acceleration,
then,
may
be
expressed
as
follows,
This
equation
maybe
stated
in
words as
follows:
If a
particle
moves
on a
path
as the
path rotates,
the
acceleration
of
the
particle
is the
geometric
or
vector
sum
of
(1)
the
acceleration
the
particle
would
have if the
path
were
fixed,
(2)
the acceleration
the
particle
would
have if
it were
fixed on the
path
as the
path
rotated,
and
(3)
2^60
called
the
compound supplementary
acceleration.
This
state-
ment is
known as
Coriolis'
law.
From
the above
derivation,
it
is seen that
2uu
is due
(1)
to
a
part
of
the
change
of
direction
of
u
} (2)
a
part
of
the
change
of the
direction of
w,
and
(3)
a
part
of the
change
of the
magnitude
of
w,
all of
which
would be absent
if the
path
were
translating
instead
of
rotating.
Thus,
as
noted at
the
beginning
of
this
article,
if
the
path
is
translated,
the
equation
a
=
a
r
+>
a
m
expresses
the
same
fact
as
does
the
equation
of
Art,
128 which
involves accelerations,
ILLUSTRATIVE
PROBLEM
328.
The
circular arc
APB
(Fig.
313a)
represents
the vane
of
a
centrifugal
pump,
P
being
a
particle
of water.
Find the
acceleration
of
the
particle
P
(V
(a)
Scale
1^=200
ft.
per
sec?
FIG.
313.
when
it is
12
in. from
0,
the
center of
the
shaft, if,
at that
instant,
the
angular
velocity
of
the
wheel
is
10
rad.
per
sec.
clockwise
and
its
angular
acceleration
is
50
rad.
per
sec.
2
clockwise.
The
tangential
velocity
of the
particle along
(relative
to)
the
vane
is
10
ft.
per
sec.
and
the
tangential
acceleration
relative

CORIOLIS'
LAW
275
to the
vane is
10
ft.
per
sec.
2
OB makes an
angle
of 45
with
the
horizontal
and is
18 in.
long;
OA is 3
in.;
and
OP
is 12
in. The
radius
of the
arc
APB
is
13
J
in.
Solution.
By
Coriolis' law
the
total acceleration
a
is,
a
=
Or
-f>
dm
+>
2lico,
a
r
and
am
are found most
easily
from
their
t-
and
n-components,
Hence,
=
10
-B-
-
4
50x
4>
10
2
x
4>
2X10X10
loj
12 12
12"
=
10
+> 90.56 4>
50
4>
100
+
200,
each of
the
quantities
being expressed
in
ft.
per
sec.
2
The
five
components
are
shown
in
their
proper
directions
in
Fig.
3
13
(a)
and the
resultant
accelera-
tion
a as found
from the
acceleration
polygon
is
shown
in
Fig.
313(6).
By
scaling
the
closing
line
of the
polygon,
a
is found
to be
145
ft.
per
sec.
2
in
the
direction
shown
in
Fig. 313(6).
PROBLEM
329.
Point P
(Fig.
314)
moves on the rod OM
which
rotates
about
the
fixed
point
0.
In
the
given position
OP
=
6
ft.;
the
velocity
along
the rod is
5 ft.
per
sec.
toward
M
and
is
increasing
at
the
rate of
5
ft.
per
sec.
each
second.
The
angular
velocity
of
the rod is
2
rad.
per
sec.
in
a
clockwise
direction,
and
is
decreasing
at
the rate
of 1.5
rad.
per
sec.
each
sec.
Find
the
acceleration
of
the
po'nt
P. NOTE.
Usescales:
lin.
=
2ft.;
1
in.
=
5
ft.
per
sec.;
1
in.
=
5 ft.
per
sec.
2
Use 8
in.
by
11
in.
paper
with
the
long edge
as
the
bottom.
Lay
the
diagram
out on left
part
of
sheet, placing
point
1
in. from the left
edge
and
2
in. from
the bottom
-p
IG
edge.
Show
all
component
accelerations of
P
to scale.
Combine
the
components
graphically, starting
at
a
point
1
j
in. from
the
top
edge
and 1
in. from
the
right
edge.
Combine
the
components
in the
order
of
(am
)
n
,
(om\,
a
r
and
2uw.
Ans.
ap
=
22.0
ft.
/sec.
2
vertically
downwards.

CHAPTER VIII
MOTION
OF RIGID
BODIES
131. Introduction.
In
the
preceding chapter
the
motion of
a
point
or
particle
and the
relation between the
motions of
two
particles
have been considered.
In
engineering problems
in
general,
however,
the
motion of
bodies,
not
particles,
must be
considered.
In some
problems,
the
dimensions of the
body
may
be
assumed
to be
negligible
in
comparison
with its
range
of
motion,
with
very
small
error,
and
hence,
the methods and
equations
of
the
preceding
chapter apply directly
to
the
motion of the
body.
This
assumption
is involved
in
a
number
of
problems
in
the
pre-
ceding chapter,
in which a
body
is assumed
to be a
particle.
In
general,
however,
the motion
of bodies as met
in
engineering prac-
tice
is
such
that the various
points
of a
body
have different
motions.
The
object
of
this
chapter
is to
analyze
certain
common
types
of motion
of
rigid
bodies
so that the
displacement,
velocity,
and
acceleration,
both
linear and
angular,
may
be
found
from the
methods and
equations
developed
in the
preceding chapter.
The
motions considered
are
translation, rotation,
and
plane
motion.
132. Translation.
Translation of a
rigid
body
is a
motion
such
that no
straight
line
in the
body
changes
direction,
that
is,
each
straight
line remains
parallel
to
its initial
direction.
Hence,
at
any
instant,
all
points
in the
body
move
along parallel
paths
and have
the
same
velocity
and
acceleration.
If
the
transla-
tion is such as
to
move
the
particles
on curved
paths
the motion is
called
curvilinear translation
as,
for
example,
the motion
of the
parallel
rod of a locomotive.
If
the
particles
move on
straight-
line
paths
the motion is called rectilinear translation.
The
body
may
have
a
uniformly
or
non-uniformly
accelerated motion.
Hence
any
point
in
a
translating body
may
have
any
of the motions
treated
in
the
preceding chapter.
Further,
since all
particles
hi
the
body
have
the same
motion
at
any
instant,
the
displacement,
velocity,
and
acceleration of the
body
is described
by
the dis-
placement,
velocity,
and acceleration
of
any particle
of the
body.
276
ROTATION
277
PROBLEM
330. A
locomotive is
running
on a
straight
track at a
constant
speed
of
40
mi./hr.
The
diameter of
the
drivers is 6 ft. and
the radius
of the crank-
pin
circle is 15
in. What
is the
magnitude
and
the direction
of the
velocity
FIG. 315.
and
of
the acceleration
of the
parallel
rod,
relative to the
engine
frame,
when
the
rod is
in
the
position
shown
in
Fig.
315?
What is the
absolute
velocity
and
the absolute
acceleration
for the same
position?
133.
Rotation.
Rotation
of
a
rigid
body
is a
motion
such
that
one
line
in the
body
(or
body
extended)
remains
fixed
in
space
while
all
points
of
the
body
describe
circular
paths
having
centers
on
the
fixed line.
The fixed line is
called the axis
of
rotation and
the
plane
in
which
the mass-center of
the
body
moves
is called
the
plane
of
motion. The
point
of
intersection
of
the
axis
of
rotation
and the
plane
of
motion
is called the
center
of
rotation.
It will
be noted
that
any
line
parallel
to
the
plane
of motion
changes
direction.
The motion of
a
body having
rotation cannot
be
defined
or
described
by
stating
the linear
displacement, velocity,
and
acceleration
of
any
point
in the
body,
as was
the case for trans-
lation,
since
all
points
in the
body
do not have the
same
linear
mo-
tion.
However,
the
angular
displacements, velocities,
and
acceler-
ation,
respectively,
are the same for all
particles
in
the
body.
Hence
the
motion
of
a
rotating
rigid
body may
be described
by
the
angular
motion
of
any
point
in
the
body.
Thus
all the
equations
in
the
preceding
chapter
dealing
with
the
angular
motion of
a
point
moving
on
a circular
path,
in
which the radius
vector
is the
radius of
the
circle,
apply
to
the
motion of a
rotating
rigid body,
as well
as to
each
point
in
the
body.
The linear
displacement,
velocity,
and acceleration
of
any point
may
also be found
from
the
equations
in the
preceding
chapter,
that
deal
with
the linear
motion of
a
point moving
on a
circular
path.

278
MOTION
OF
RIGID
BODIES
PROBLEMS
331. A
straight
stick
4
ft.
long
rotates
in
a
horizontal
plane
about
a
ver-
tical
axis
through
one end of the
stick. Its
angular velocity
changes
uniformly
from 20
to 50 r.
p.m.
in 5
sec.
What
is the
linear
velocity
of its
mid-point
at
the
end
of
2
sec.?
332. The
flywheel
of
a
punching
machine fluctuates from
100
to 80
r.p.m.
at a
uniform rate when a hole is
punched.
If
the
flywheel
makes
1|
revolu-
tions
while this
change
of
speed
takes
place,
how
long
does it
take
to
punch
the hole?
Ans. t
=
1
sec.
333.
The
flywheel
of
a
rolling-mill engine
is 14 ft. in
diameter. Just
before
the steel is
fed hi the rolls the
speed
of
the
flywheel
is
90
r.p.m.
As the
steel enters the
rolls the
speed
decreases
uniformly
during
|
sec.,
before the
governor
can
operate.
If
the
angular
acceleration
(negative)
of the
flywheel
is 20
r.p.m. per
sec.,
what
is the
decrease
in the
speed
of
the
flywheel,
expressed
in
r.p.m.?
134. Plane
Motion.
Plane motion of a
rigid
body
is a
motion
such that
each
point
in
the
body
remains at a
constant
distance
from a
fixed
plane.
The
motion of the
connecting
rod of a
steam
engine
is an
example
of
plane
motion. The
wheels of a
locomotive
when
running
on
a
straight
track also have
plane
motion. A
plane
parallel
to
the fixed
plane, containing
the
mass-center
of the
body,
is called
the
plane
of
motion.
It is
evident that a
rotation
is
always
a
special
case of
plane motion,
whereas a
translation
may
or
may
not
be
a
plane
motion.
In
plane motion,
in
general,
a
straight
line
in
the
body lying
in
the
plane
of motion
changes
direction
and, hence,
the
body rotates,
but not
about a fixed axis.
The
body,
therefore,
has
angular
mo-
tion,
and
its
angular displacement,
velocity,
and
acceleration are
the
same as that
of
any straight
line in the
body,
in
the
plane
of
motion,
since
all
such
lines have the same
angular
motion if the
body
is
rigid.
The
angular
motion of
the
body, therefore,
may
be
studied
by
means
of the
same
equations
that
apply
to
the
rotation
of a
rigid body
about a
fixed axis.
Rotation, however,
is
only
one
part
of the motion of a
rigid
body having plane
motion
(except
in a
special
case as
noted in the
next
article).
Plane motion of a
rigid body may
be
resolved into
two
component
motions,
a
rotation and a
translation,
according
to the
following
theorem:
Plane
motion
of
a
rigid
body,
at
any instant,
is a com-
bination
of:
(1)
a
pure
rotation of
the
body,
about an axis

PLANE
MOTION
279
(perpendicular
to the
plane
of
motion)
passing
through
any
point
B in the
body,
with
an
angular
velocity
and
acceler-
ation
the
same as
that which the
body
has at
the
instant;
and, (2)
a translation
of the
body
which
gives
to each
point
the same
linear
velocity
and
acceleration
that the
point
B
has at
the instant.
The
point
B is called the
base
point.
It is
evident
that all
points except
the
base
point
have two
motions;
a rotation
about
the
base
point,
and
a
motion the same as
that of the base
point.
From
the
analysis
of the motion
according
to the
above
theorem,
the
displacement,
velocity,
and acceleration of
any
point,
A,
in
the
body may
be found
from
the
equations
developed
in
Art.
128
of
the
preceding chapter.
The
equations
are,
V
B
To arrive
at
the above
theorem,
consider the motion of
the
connecting
rod of a steam
engine (Fig.
316).
Let
P
denote
the
position
of
the crosshead
and
Q
that
of
the
crank-pin,
the crank
being
of
length
OQ.
When
the
crank moves
from
position
OQ
FIG.
316.
to
position
OQi
the
connecting
rod moves from
position
PQ
to
position
PiQi.
This
change
of
position
can
be
given
the rod
by
first
rotating
the rod about
P,
until it
becomes
parallel
to its new
position,
and
then
giving
the
rod
a
translation such
that each
point
receives
a
displacement equal
to
PP\'.
By
this
combina-
tion of motions
the
point
P
moves
along
its actual
path
but
any
other
point
does
not travel
in
its actual
path.
The
point
Q,
for

280
MOTION
OF RIGID
BODIES
example,
moves
along
the
path
QQ'Qi
instead of
its actual
circular
path
QQi.
However,
as
the
change
of
position
is
made
smaller
and
smaller,
the
path
QQ'Qi
approaches
the
circular
path
QQi
and,
in' the
limit,
as the two
motions
are
generated
simultaneously,
each
point
is made to move
on its actual
path
by
successive
combinations
of
a
proper
rotation and a
proper
translation.
The
rotation,
at
any
instant,
must
give
the
b9dy
its
actual
angular
velocity
and
acceleration
at
the
instant,
since
the
translation
does not
influence
the
angular
motion of the
body.
The
transla-
tion
must
give
all
points
of
the
body
the same motion
that
the
base
point
has at
the
instant,
since the base
point
receives
its
total
motion
from
the translation.
By
the
above
method,
the rod is
given
a
rectilinear
transla-
tion,
since
the
point
P moves on a
straight-line path.
If,
how-
ever,
another
base
point
is chosen
as,
for
example,
the
point
Q,
FIG.
317.
the
change
of
position
from
PQ
to
PiQi
may
then be made
by:
(1)
a rotation
about
Q
(Fig. 317);
and,
(2)
a curvilinear transla-
tion
giving
to each
point
the same
motion that
Q
has.
By
this
combination
of
a rotation and
a
translation the
point
P is made
to
take the
path
PP'P\
instead of its
actual
path
PP\
y
but, reasoning
as
above,
if the
change
of
position
is made smaller and
smaller
the
path
PP'P\
approaches
the
path
PP\
and,
in the
limit,
as
the
two motions
are
imposed
simultaneously,
each
point
in
the
body
is
given
its exact
motion at
any
instant.
Likewise,
any
other
point
in
the
body may
be selected as the base
point.
And,
the
plane
motion of
any
other
rigid
body
may
be
treated
in like
manner.
Hence,
a
plane
motion of a
rigid body
may
be
consid-
ered,
at
any
instant,
as a
combination of
a rotation
of
the
body
about
any
base
point
in
the
body,
with an
angular
velocity
and
acceleration
equal
to
the
angular
velocity
and acceleration
that
the
body
has
at the
instant,
and a
translation of
the
body
that
