Seely F.B. Analytical Mechanics for Engineers
Подождите немного. Документ загружается.

EQUATIONS
OF MOTION FOR A
PARTICLE
301
By
substituting
this value of T
in
(4),
the
value of
v
may
be found.
Thus,
4.62 cos
aO'-^Xj^jp.
Hence,
4.62X0.5X32.2X5X0.5
AB9
V
i=
;
=
4b.O.
4
Therefore,
v
=
6.8
ft.
/sec.
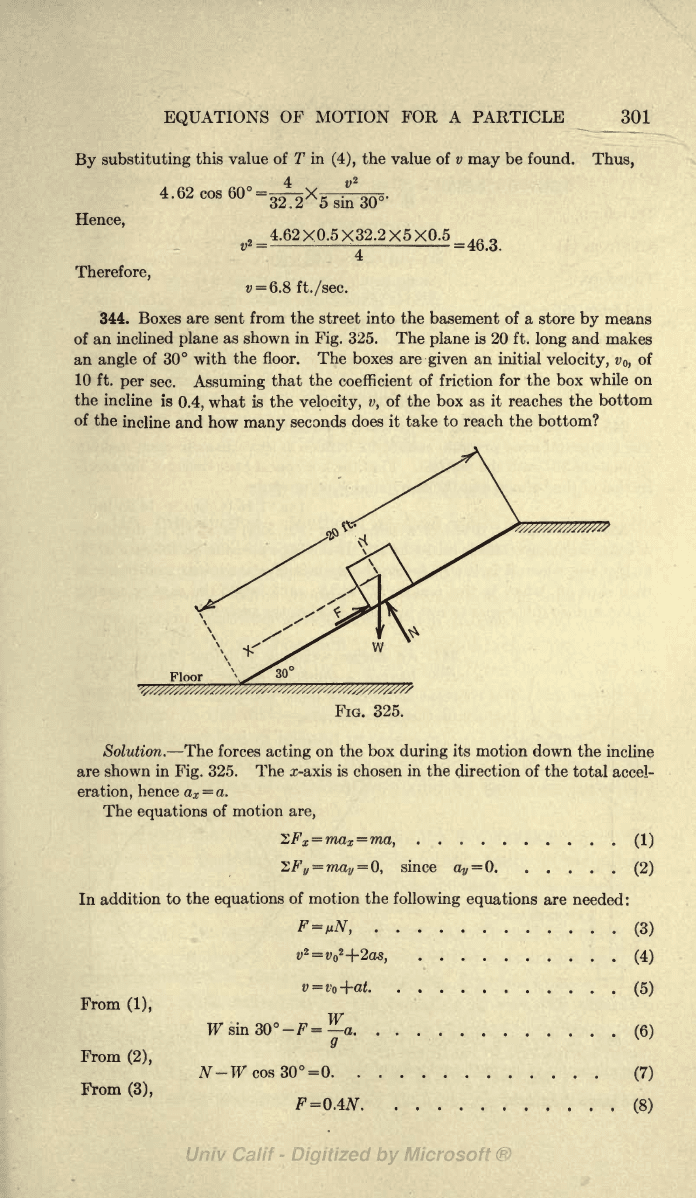
344.
Boxes are sent from the street
into
the
basement of a
store
by
means
of an
inclined
plane
as shown in
Fig.
325. The
plane
is 20 ft.
long
and
makes
an
angle
of
30
with
the
floor.
The
boxes are
given
an initial
velocity,
v
,
of
10
ft.
per
sec.
Assuming
that
the
coefficient
of
friction
for
the box while
on
the
incline
is
0.4,
what is
the
velocity,
v,
of the
box as it reaches
the
bottom
of
the
incline and how
many
seconds
does
it
take to reach the bottom?
XX^%xxJ<<xxx?xJ^
FIG.
325.
Solution.
The
forces
acting
on
the box
during
its
motion down
the
incline
are shown
in
Fig.
325.
The z-axis is
chosen
in
the direction
of the
total
accel-
eration,
hence
a
x
=
a.
The
equations
of
motion
are,
SF^
=
ratty
=
0,
since
ay
=
(2)
In addition
to the
equations
of motion the
following equations
are
needed:
F
=
^,
(3)
v
=
vo+at
(5)
From
(1),
TFsin30-F=-a
(6)
From
(2),
AT-
W cos
30
=0
(7)
ftomW,

302
FORCE,
MASS.
AND
ACCELERATION
Substituting
the
value of
F
from
(8)
and
(7)
in
(6)
we
obtain,
Therefore,
And
from
(4)
Therefore,
And
from
(5),
Therefore,
a
=
4.95
ft./sec.
2
y2
=
(lO)
2
+2X4.95X20.
v
=
17.3
ft./sec.
17.3
=
10+4.95*.
2
=
1.47
sec.
PROBLEMS
345.
A balloon
weighing
400
Ib.
has a vertical acceleration of
2
ft.
per
sec.
2
The
horizontal
wind
pressure
causes the balloon to
travel
in
a direction
making
an
angle
of
30
with
the
vertical.
Find the
horizontal
component
of the
accel-
eration
of the
balloon and
the horizontal wind
pressure.
Ans. 1.15
ft./sec.
2
;
14.35 Ib.
346.
The
winding
drum of a
mine
hoist
(Fig.
326)
is
15 ft. in
diameter.
A
cage
weighing
8
tons is
raised
by
it. If the
cage
is
rising
at the rate
of
60
ft.
per
sec.
when
it
is 104
ft. below the surface of the
ground,
and
power
is
then
shut
off,
what is
the
tension, T,
in the
cable while the
cage
is
coming
to
the surface
if
it
comes to rest
just
as it reaches the
surface?
Ans. 7410
Ib.
347. An
engine weighing
64.4
tons travels
round
a
curve
having
a constant
radius of
1000
ft.,
at a
constant
speed
of 45 miles
per
hour.
Find the hori-
zontal
thrust
on the
rails.
=
60
ft./
sec.
D
FIG.
326.
FIG.
327.
348.
In
"
looping
the
loop
"
(Fig.
327),
show that if friction is
neglected,
the
minimum
value
of
the
velocity
of the car when at
C is
A/^-
if the
car
does
not leave
the
track.

INTRODUCTION. METHODS OF
ANALYSIS
303
349.
A
small
body
weighing
12 Ib.
rests on an inclined surface
(Fig.
328)
which
is revolved about a vertical
axis with a constant
angular
velocity
of
20
r.p.m.
If
the
body
is attached to
the axis of ro-
tation
by
a cord as shown
in the
figure,
and if
friction
between the
body
and
plane
is
neglected,
find the
tension, T,
in the cord.
350.
A box is
projected
up
an inclined
plane,
which
makes
an
angle
of 20 with the
horizontal,
with
an initial
velocity
of 2400 ft.
per
minute.
If
the coefficient
of kinetic friction is
0.2,
how
far
up
the
plane
does
the box
travel
before
coming
to
rest? Will the box remain at rest?
If
not,
how
long
does
it take it to reach
the bottom
of the incline?
FIG. 328.
Ans. s=46.9 ft.
2.
KINETICS
OF BODIES
144. Introduction. Methods of
Analysis.
As
stated
in
the
preceding
section,
the
general
character
of a
problem
in
kinetics
of bodies
is
the same whether the
body
has
a motion of
translation,
of
rotation,
or of
plane
motion:
A
physical body
is
acted
on
by
a
force
system
that has a
resultant which causes
a
change
in
the
motion of the
body.
For each
type
of
motion,
relations are
found
between
(1)
the resultant
of the external force
system,
(2)
the
properties
of the
body (mass,
moment
of
inertia, etc.),
and
(3)
the
change
in
the motion of
the
body.
For each
of the
types
of
motion of
rigid
bodies treated
in
this
section,
the
equations
which
express
the relations between the three factors or elements
in
the
problem
(equations
of
motion)
are
found
by
the same
procedure
or
series of
steps,
as
follows:
1. From
the
motion of
the
body,
the
acceleration, a,
of
any
(and
every) particle
in
the
body
is
found,
both
in
magnitude
and
in
direction.
This
step
involves the use of the
equations
of
kinematics
as
developed
in
Chapters
VII and
VIII.
2. From the
acceleration,
a,
of
any
particle
and
its
mass,
m,
the
force
required
to
produce
the
acceleration
is
found,
both
in
magnitude
and
in
direction,
by
applying
Newton's
second law.
This
force,
R,
is
expressed by
the
equation
R
=
ma,
its
direction
being
the same
as that of
a.
This
force is called the
effective
force
for the
particle
and
is,
of
course,
the
resultant
of the actual
forces
acting
on
the
particle.
Some
(most)
of
the
particles
of a
body
are acted on
by
internal forces
only (in
addition to their
weights),

304
FORCE,
MASS,
AND ACCELERATION
that
is,
by
the
neighboring particles
of
the
body,
and
some of
the
particles
are acted
upon
by
both internal and
external
forces.
The
effective
force for
a
particle,
therefore, may
be
the
resultant
of
internal
forces
only
or of
internal and
external
forces.
3.
The
magnitude
and
the direction of the
effective
force for
each
particle
of the
body having
been
determined,
in terms of the
mass and
acceleration
of the
particle,
the
resultant of
the
effective
forces
for
all
the
particles
of the
body
is
found
completely by
the
same methods
as
were
used
in
Chapter
II for
finding
the resultant
of
a
given
system
of
forces. The effective
forces
for
bodies
having
the
motions considered
in
this section
may
be assumed to form a
coplanar
force
system.
1
Therefore,
the resultant of the effective
forces,
in
general,
may
be determined
by writing
three
equations
(Art. 30) involving
the
summations of
the
x-components
of the
effectives
forces,
of the
^/-components
of the
effectiye
forces,
and
of
the
moments
of the effective forces about
an
axis
in
the
body.
4.
The
equations
obtained
in
step 3,
which determine
the
resultant
of the effective forces
for the
whole
body,
contain all
the internal
forces and
all the
external
forces
which
act
on
all of
the
particles.
But,
in
obtaining
the summations of
the x- and
of
the
^/-components
and of
the moments of the
effective
forces,
the
internal
forces
drop
out
of
the
expressions
since
they
occur
in
collinear
pairs,
the forces
of each
pair being
equal
and
opposite
(Newton's
third
law). Hence,
the sum
of their
components
in
any
direction and the
sum of their
moments
about
any
axis
are
zero.
Therefore,
The
resultant
of
the
effective forces
for
the
particles
of a
1
In
the
discussion
of
translation,
in this
section,
the motion will
be restricted
to a
uniplanar
translation.
Further,
the bodies considered
in
connection
with
the three
types
of
motion discussed
in this
chapter
will be assumed to
be
homogeneous
and
to have
planes
of
symmetry
which are the
planes
of motion
of
the bodies
(Arts.
133
and
134)
and
hence,
in
discussing
the kinetics of such
a
body having
a
motion of translation
or
rotation,
or
a
plane
motion,
the mass
of the
body may
be assumed to
be
concentrated
in
the
plane
of motion.
Thus,
the
body
may
first be
imagined
to be made
up
of
elementary
rods
perpendicular
to the
plane
of
symmetry
and then each rod
may
be
imagined
to
be
squeezed
or
compressed
without
having
its
cross-sectional area
changed,
until the
rod
becomes
an elemental disc
lying
in the
plane
of
symmetry
and
having
the same
mass
as does
the
elementary
rod.
Therefore,
the
effective
forces
may
be con-
sidered
to form a
coplanar
force
system
in
the
plane
of
motion of the
body.
If
the
body
does
not have a
plane
of
symmetry,
more
than
three
equations
are
needed
to
define its motion
completely.

KINETICS
OF A TRANSLATING
RIGID BODY
body
is identical with
the
resultant of the external forces
which
act on
the
body.
Or,
The resultant
of the effective
forces for
all
the
particles
of
a
body,
if reversed
and assumed
to act on
the
body
with
the external
forces,
will
hold the
body
in
equilibrium.
This
is a
statement
of D'Alembert's
principle.
It will be
noted,
therefore,
that
D'Alembert's
principle
makes it
possible
to
reduce
a
problem
in
kinetics
to an
equivalent
problem
in
statics
by
intro-
ducing
a force
(or forces)
which
may
be found
completely
from the
motion
of
the
body by
means of the first
three
steps
outlined above.
TRANSLATION
145. Kinetics
of a
Translating Rigid Body.
If
a
rigid
body
is
acted on
by
an unbalanced force
system
that causes
a
motion of
translation,
the
resulting
accelerations of
all the
particles
of the
body
are the
same,
both
in
magnitude
and
in
direction
(Art. 132).
And,
whenever
a
particle
of
a
body
is
accelerated,
a resultant force
must act on
the
particle.
This
force,
as
already noted,
is called
the
effective force for the
particle.
The
magnitude
of the
effective
force is the
product
of the
mass,
m,
of the
particle
and
its accelera-
tion, a,
and its direction is the same as that
of
a
(R
=
ma from
Newton's
second
law). Therefore,
the effective
forces for
the
particles
of a
translating
rigid
body
form
a
parallel
system
and,
since all of the forces have the
same
sense,
their resultant
must
be a
single
force
(never
a
couple),
the
direction
of
which is the
same as
that
of
each
of
the
effective
forces.
And,
as
noted
above,
if
the
body
is
symmetrical
with
respect
to
a
plane
through
the mass-
center
(plane
of
motion),
the
parallel
forces
may
be
treated as a
coplanar
parallel
system (see
footnote
under Art.
144).
Thus,
let
the
rigid
body
represented
in
Fig.
329
(a)
be
given
a
rectilinear
translation
along
a
smooth
plane
by
the
force
P
which
produces
the
acceleration, a,
of each
particle
of
the
body.
Let
the
body
be made
up
of sixteen
small
cubes
(representing
the
particles
of
the
body)
attached
(glued)
so that
they
move as a
rigid
system.
The cubes
may
be
made of
different
materials
and
hence
their
masses are not
necessarily
equal.
For
convenience,
each
cube will
be
thought
of as
a
particle.
The
effective
force for
the first
par-
ticle is
m\a,
for the
second
particle,
m<2,a,
etc.
The
sixteen
effect-
ive forces form
a
coplanar parallel system
as
shown.

306
FORCE, MASS,
AND
ACCELERATION
Resultant
of Effective
Forces.
The
resultant of
these
effective
forces
may
be found in
magnitude,
action
line,
and
sense
by
the
method
used
in
Art. 26
for
finding
the
resultant of
a
sytem
of
parallel
forces
in
a
plane.
Thus,
the
resultant
of
the
effective
forces is a
force
having
a
magnitude equal
to
the sum of the
forces,
its sense
being
the same
as that
of the
common acceleration.
Hence,
The
magnitude
of the resultant of
the
effective forces
=
2raa
=
Ma
o
r- direction
(a)
'
1
fit
Ma
W
(6)
FIG. 329.
in
which
M
denotes
the mass of the whole
body,
that
is,
the sum of
the
masses
of the
particles
(M=2m)
and
a is the
acceleration,
which
is
common to
all the
particles
and
hence
is
a
constant and
may,
therefore,
be taken outside
the summation
sign.
The
action
line of
the resultant
of the effective forces
is located
by
use
of
the
principle
of
moments
(Art.
25). Thus,
in
Fig.
329(6),
the
sum of
the
moments of
the effective
(ma)
forces about
any point,
0,
must
equal
the moment
of
their resultant
(Ma)
about
the same
point.
Hence,
if
y
denotes
the
moment-arm
of
the effective
force
for
any particle
with
respect
to
0,
and
p
denotes
the
moment
arm
of
the
resultant
Ma
with
respect
to
0,
the
principle
of moments
is
expressed
by
the
equation,
That
is,
Therefore,
2(my)=Mp,
since
a is
constant.
p=^ir-

KINETICS
OF
A
TRANSLATING
RIGID
BODY
307
This
equation
shows,
however,
that
the resultant
of the
effective
forces
passes
through
the
mass-center
(and
not
as
shown
in
Fig.
3296)
since the
expression
for
p
is also
the
expression
for
the
?/-coor-
dinate
(y)
of
the mass-center
(Art. 85).
Relation
between
Effective
Forces and
External
Forces.
The
relation between
the
resultant of the
effective
forces and the
resultant
of the
external
forces
which
act on
the
body may
now be
found.
The resultant
of the effective
forces is
the resultant of
all
the
forces
acting
on all the
particles
and
hence
includes
all of
the
internal
forces and
all of
the external
forces.
Therefore,
if F
T
denotes
the
component
of
a force
parallel
to the
direction
of
a,
we
may write,
(SF
r
)
External^
(Sf
r
)
internal
=
S(ma)
=
Ma.
However,
in
obtaining
the summation of
the
r-components
of all
the effective
forces,
the
sum
of
the
r-components
of the
internal
forces
becomes
zero
since the
internal forces
occur
in
pairs
of
equal,
opposite,
and collinear
forces
(Newton's
third
law).
Therefore,
the
resultant of the external forces is identical
with
the resultant
of the
effective
forces
(D'Alembert's
principle).
That
is,
it has
the
same
magnitude,
action
line,
and
sense as the
resultant of the
effective
forces.
Hence,
the
magnitude
of the
resultant of the
external forces
(2F
r
)
is
given
by
the
equation
Thus,
the
resultant of the external
forces
(P,
W,
and
N)
is
represented completely by
the force
Ma
in
Fig. 330(a).
Or,
to
express
the same idea
in
other
words,
if
an
additional
force
were
acting
on the
body
with the external
forces
P, W,
and
TV,
the
mag-
nitude
and the
action line of the additional
force
being
the same as
the
magnitude
and
the
action
line of
the
resultant
(Ma)
of
the
effective
forces,
but
reversed
in
sense
(opposite
to
a),
as
shown
in
Fig.
330(6),
then the forces
acting
on
the
body
would be in
equilibrium.
This
additional
(imaginary)
force is
sometimes
called the reversed
effective
force
for
the
body
or the
inertia
force
for the
body.
It will
be
noted
that
the normal
pressure
N
cannot
be collinear with
W
when
the
force
P
has
the
action
line
as
given
in
Fig.
330(6).
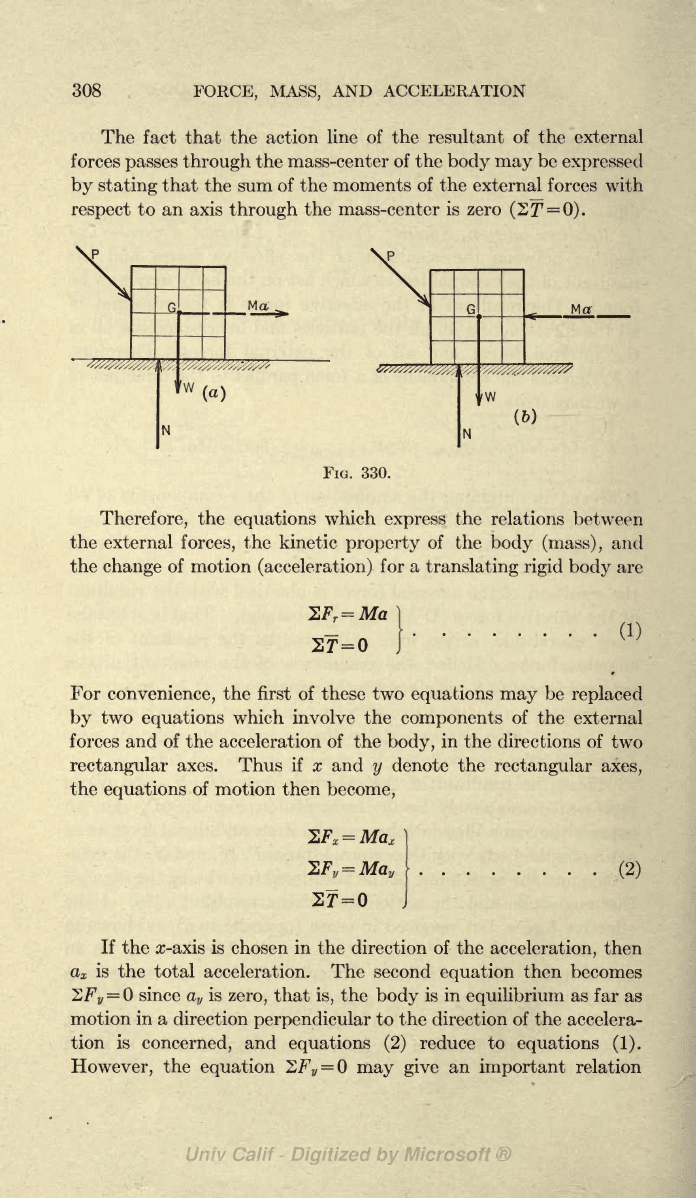
308
FORCE, MASS,
AND
ACCELERATION
The fact that the action
line
of
the resultant
of the external
forces
passes
through
the
mass-center
of the
body may
be
expressed
by
stating
that the sum of the
moments
of the
external forces
with
respect
to an axis
through
the
mass-center is zero
(S7
T
=
0).
\
Ma
I
Ma
FIG. 330.
Therefore,
the
equations
which
express
the
relations
between
the external
forces,
the kinetic
property
of
the
body
(mass),
and
the
change
of motion
(acceleration)
for a
translating rigid body
are
(1)
For
convenience,
the
first of these
two
equations
may
be
replaced
by
two
equations
which
involve the
components
of the
external
forces and of the acceleration of the
body,
in
the
directions of
two
rectangular
axes. Thus if x and
y
denote the
rectangular axes,
the
equations
of motion then
become,
(2)
If
the
x-axis is chosen
in
the direction of the
acceleration,
then
a
x
is
the total
acceleration. The second
equation
then
becomes
2F
y
=
since a
y
is
zero,
that
is,
the
body
is
in
equilibrium
as far as
motion
in
a
direction
perpendicular
to the direction of the
accelera-
tion is
concerned,
and
equations
(2)
reduce
to
equations
(1).
However,
the
equation
SF
tf
=
may
give
an
important
relation

KINETICS
OF
A TRANSLATING
RIGID BODY
309
between
the forces
in
the
solution of a
particular problem. Further,
it is
sometimes
convenient
to select x-
and
i/-axes
neither
of
which
agree
in
direction
with the acceleration.
Equations
(2)
therefore,
will,
as a
rule,
be used
and
referred to
as
the
equations
of
motion
of a
translating rigid
body.
NOTE.
In
analyzing
and
solving
problems
in
kinetics of
bodies,
the same
general procedure
should be
followed
as was outlined in
the note at the
end
of Art.
143.
ILLUSTRATIVE
PROBLEMS
351.
The dimensions
of
block
A
(Fig.
331)
are 3 ft.
by
3
ft.
by
5 ft. and
the
weight
of
the block
is
1200
Ib. The
block
rests
on
a
carriage, B,
which
is
given
an acceleration
a in
the
direction
shown.
If
the friction
between the block and car-
riage
is sufficient
to
prevent
slipping,
what is the
maximum
acceleration
that
the
carriage
can
have
without
causing
the
block to
tip
over?
Solution.
The block
has a
motion
of
translation
under
the
action of two
forces,
namely,
the
weight,
W,
and
the
reaction,
R,
of
the
carriage.
For convenience
the latter
force,
which acts at
when
the
block is
on the
point
of
tipping,
will
be
resolved into the
normal
pressure,
N,
and
the frictional
force,
F,
as
indicated
in
the
figure.
The
equations
of
motion
for
the block
are,

310
FORCE,
MASS,
AND
ACCELERATION
By
solving (5)
and
(6)
for F
and
substituting
its
value in
(4),
the
values of
F
and a
become,
F
=
7201b.,
a
=
19.32ft./sec.
2
Second
Method.
Inertia
Force
Method.
If
the
inertia
force
(reversed
effective
force)
for
the
body
is
assumed to act on
the
body
with
the
external
forces,
the
body may
be
assumed to be in
equilibrium
(D'Alembert's
principle)
and
hence the
equations
of
equilibrium
may
be
applied
to the force
system
thus
formed.
The
inertia force for the
translating
block A
is,
1200
Ma
=
32.2
Its
direction
is
opposite
to that of a
and its
action line
passes through
the mass-
center of the
block.
Therefore,
the
forces
acting
on the block
as shown
in
1200
32.2
W
|=1200
Ib.
(B)
120 ib.
FIG.
332.
FIG.
333.
Fig.
332
will hold the block
in
equilibrium.
The
equations
of
equilibrium
for the force
system
(Art.
50)
are,
1200
y
=
N-1200
=
0,
^
=
0.
The
solution
of the
equations
leads to the same results as were
found
by
the
first
method
of
solution.
It should
be noted that
in
obtaining
the
moments
of
the
forces
in the
above
equilibrium
equation
(SM
=
0),
the moment-center
O
may
be
taken
as
any
point
in
the
plane
of the
forces,
whereas the moments of
the forces
in
the third
equation
of
motion
(2^
=
0)
used
in
the first method of solution
must
be
taken
about
the mass-center of the
body.
352.
Three
bodies
A, B,
and C are
connected
by
two
cords
as
shown
in
Fig.
333
so
that
all three
bodies
move with the same
acceleration.
The
pulley,
