Seely F.B. Analytical Mechanics for Engineers
Подождите немного. Документ загружается.


KINETICS OF
A
ROTATING
RIGID
BODY 321
Referring
to the
free-body
diagram
for
the rod
(Fig.
342&)
we obtain:
From
(1),
From
(2),
From
(3),
32.2
12
\
60
/
P-ft+16.1
si
(16.1
cos
60+P)
|
=
7,
|X^X
^40.
. .
Solving
(4)
we
obtain,
Solving (6)
we
obtain,
(4)
.
(5)
(6)
R
n
=
18.9 Ib.
P
=
36.41b.
Substituting
the
value
of
P
in
(5)
and
solving
for
ft
we
obtain,
ft
=
11.1
Ib.
Therefore,
364. In
Fig.
343,
CD
represents
a
brake for
regulating
the descent
suspended
body,
A.
B
is the
drum
from
which
the cable attached
to
winds
as A
descends. The
radius,
n,
of the
drum is
6 ft. The
radius, r^
of
the
brake wheel
is 7 ft.
The
radius of
gyration,
k
,
of
the
rotating
parts (drum
and
brake
wheel)
about the
axis
of ro-
tation is
4
ft. The
rotating
parts
weigh
2000
Ib.
and
the
body
A
weighs
1000 Ib.
The
coefficient of
brake
fric-
tion
is
J.
If
friction on
the
axle of
the
rotating
parts
is
neglected,
find the
acceleration, a,
of the
body
A,
the
tension, P,
in
the
cable,
and the
hori-
zontal
and
vertical
components,
ft
and
ft,
of the axle
reaction,
assuming
the
force at C to
be
100
Ib.
(Consider
the
cable to
be
flexible
and
neglect
its
weight.)
of the
A un-
FIG. 343.
Solution.
Three
bodies are to be
considered,
(1)
the brake CD
which
is in
equilibrium,
(2)
the
drum
and
the
brake wheel which have a
motion of
rotation,
and
(3) body
A
which
has
a motion of
translation.
The
free-body
diagram
for
each
body
is
shown in
Fig.
344.
The
brake is
held in
equilibrium
by
a
non-concurrent
force
system
in
a
plane
for
which the
equations
of
equilibrium
are:
SP*
=
0,
. .
(1)
(2)
(3)

322
FORCE,
MASS,
AND
ACCELERATION
Equation
(3)
only
is needed
in
this
problem
since all of the
forces
acting
on
the brake
are not
required.
The
equations
of motion for the
drum
and brake wheel
are:
(4)
(5)
(6)
In addition
to
these
equations
the
denning
equation
of the
coefficient of
friction
must
be
used, namely,
F=nN
(7)
N N
Qi
(b)
FIG. 344.
1000
lb.
a.y
=
a
=
at
Applying
the
equations
we have:
From
(3),
One
equation
of
motion
only
is needed
for
body
A,
namely,
Further,
since the
total acceleration of
body
A is in the
?/-direction
and since
it has the same
magnitude
as the
tangential
acceleration,
at,
of a
point
on the circumference
of the
drum,
we
may write,
(9)
Whence,
From
(7),
100X4.5-0.5AT
=
0.
AT
=
900 lb.
7^
=
1X900
=
225 lb.

KINETICS
OF
A
ROTATING
RIGID
BODY
323
From
(4),
Whence,
From
(6),
From
(8),
#i-900
=
0,
since
r=0.
#i
=
9001b.
^2000,
~32.2
32.2
(10)
(ID
Substituting
-
from
(9)
for a in
(10)
and
replacing
a
y
in
(11)
by;a
from
(9),
we
have,
6P
_
225x7=
|oo
xl6x
f,
and,
And,
from
(5),
1000
-P
=
1000
32.2""
R
2
-P
-225
-2000=0,
since
r=0.
These last
three
equations
contain
the
three
required
quantities.
The
solution
of
the
equations
gives,
a
=
12.54ft./sec.,
P
=
6091b.,
#
2
=
28341b.
365.
Two
spherical
balls are
connected
by
a
light,
slender, rigid
rod
and
made
to
rotate
in a horizontal
plane
about a vertical axis
midway
between
the
balls
as
shown
in
Fig.
345.
Each
sphere
is
12 in.
in
diameter
and
weighs
64.4 Ib.
What
turning
moment
must a
couple
have which
gives
the
spheres
an
angu-
lar
velocity
of
30
r.p.m.
in 4
sec.,
starting
from
rest? If
one
of
the two
forces
of the
couple
is
applied
9 in.
from
the
axis
of rotation
and
the
other
force
is the
reaction
of
the
axis,
what
is
the
magnitude
of each
force?
Solution.
Since
the
two
spheres
have
a
motion
of rotation
the
equations
of
motion
are,
=
0,
since
r=0,
FIG.
345.
(1)
(2)
(3)

324
FORCE, MASS,
AND
ACCELERATION
Letting
the
moment of
the
couple
be denoted
by
C
and
the
mass of
each
sphere
by
M
we
have,
from
(3),
But,
from
definition,
Therefore,
And
since,
then
Whence,
x
64 ' 4
5
X
32T2
=
6.65<*.
W-COO
30X27T
i
60X4
C
=
6.65X0.785
=
5.23 Ib.-ft.
64 ' 4
=
0.785
rad./sec.
2
6.971b.
PROBLEMS
366. A solid
sphere
15
in.
in
diameter
revolves with
an
angular
velocity
of
500
r.p.m.
about
a fixed
axis which
passes through
its
center.
What
force
acting tangent
to its surface
will
stop
the
sphere
in
5
sec.
if
friction on
the
axis is
neglected?
The
weight
of the
sphere
is 500
Ib.
Ans. 40.6
Ib.
t
367. A
weight
of
30
Ib. is
suspended
from
a solid
homogeneous
cylinder
by
a
weightless
cord
which is
wrapped
around the
cylinder.
The
cylinder
weighs
193.2
Ib. and its
radius is
18 in.
Bearing
friction is
18 Ib. and
the
diameter of
the
shaft on which the
cylinder
rotates
is 4 in. If the
suspended
weight
has an
initial
velocity
of 10 ft.
per
sec.
downwards,
what will be
its
velocity
after
it
has
moved
10
ft.? What time
is
required
to move the 10
ft.?
368.
A
body
C
weighing
10
Ib.
rests
upon
a frame D
(Fig.
346)
which
rotates
about a
vertical
axis
AB,
When
the frame
is not
rotating,
the
tension
in the
spring, S,
is 20
Ib.
If
the
angular
velocity
of
the frame
is
30
r.p.m.
and
the friction
under C
is
neglected,
what is the
pressure
against
the
stop
at
El Ans.
10.8
Ib.
369.
If
the rocker
arm
BCE
in
Prob. 363 carries
on
its outer
end E
a
spherical
ball
which
weighs
4
Ib.,
find
the
values
of
P,
Rt,
and R
n
,
assuming
that
the ball
is small
enough
to be
considered
as a
particle.
370.
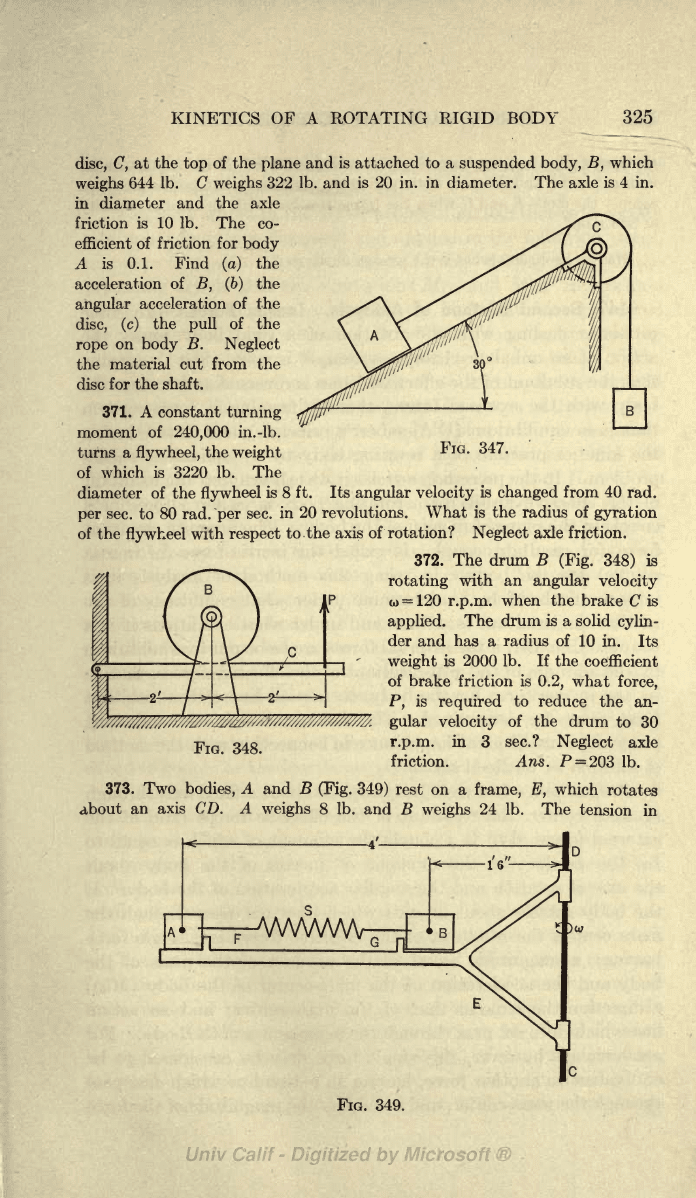
A block A
(Fig.
347)
weighs
257.6
Ib.
and rests on a
plane
inclined
30 with
the
horizontal.
A flexible
rope
attached to the
block
passes
over
the
FIG.
346.
KINETICS
OF A ROTATING RIGID BODY
325
FIG. 347.
disc, C,
at the
top
of the
plane
and
is
attached
to a
suspended body,
B,
which
weighs
644
Ib. C
weighs
322
Ib. and is 20
in. in
diameter.
The
axle
is 4 in.
in diameter
and the axle
friction
is 10 Ib. The co-
efficient
of friction
for
body
A is 0.1.
Find
(a)
the
acceleration
of
B,
(6)
the
angular
acceleration of the
disc,
(c)
the
pull
of the
rope
on
body
B.
Neglect
the
material cut
from
the
disc
for the shaft.
371.
A constant
turning
moment
of
240,000
in.-lb.
turns a
flywheel,
the
weight
of which is 3220 Ib.
The
diameter
of
the
flywheel
is
8
ft. Its
angular velocity
is
changed
from 40
rad.
per
sec. to 80 rad.
per
sec.
in 20 revolutions.
What
is the radius
of
gyration
of the
flywheel
with
respect
to
the axis
of rotation?
Neglect
axle friction.
372. The drum
B
(Fig.
348)
is
rotating
with an
angular
velocity
o>
=
120
r.p.m.
when the
brake
C is
applied.
The
drum
is a
solid
cy
Un-
der
and
has a radius of
10 in. Its
weight
is 2000 Ib. If the
coefficient
of brake friction
is
0.2,
what
force,
P,
is
required
to
reduce the an-
gular
velocity
of
the
drum
to
30
r.p.m.
in
3
sec.?
Neglect
axle
friction. Ans.
P
=
203
Ib.
FIG.
348.
373.
Two
bodies,
A
and
B
(Fig.
349)
rest on a
frame,
E,
which
rotates
about
an
axis
CD.
A
weighs
8 Ib.
and
B
weighs
24
Ib. The
tension in
FIG.
349.

326
FORCE, MASS,
AND ACCELERATION
the
spring,
$,
when
the frame is not
rotating
is
30
Ib. If the
friction under
bodies
A
and
B and the
mass of
the
spring
are
neglected,
what are the
pressures
against
the
stops
F
and
G when the frame
revolves with an
angular
velocity
of
30
r.p.m.?
374.
In
Prob.
365,
what
is the tension
in
the rod?
147.
Second
Method
of
Analysis.
Inertia Forces. In
some
problems
dealing
with
the
rotation of a
rigid
body
under
the
action
of an
unbalanced
force
system,
it
is
convenient to
assume
that
the resultant
of the
effective forces is reversed
and acts
on the
body
with
the external
forces,
thereby forming
a force
system
that
is in
equilibrium
(D'Alembert's
principle),
and thus
reducing
the
kinetics
problem
of a
rotating
body
to an
equivalent
statics
problem.
In
the
preceding
articles
it
was
shown
that
the
resultant
of the
effective
forces for a
rotating body
is
either a
force or
a
couple
in
the
plane
of motion of the
body.
The
reversed
resultant
force
(or
resultant
couple)
is called
the inertia
force
(or
inertia
couple)
for
the
body.
In
using
this
method of
analysis
it is
important,
therefore,
to determine under
what
conditions of
the
motion
the
resultant
is a force and under
what
conditions it
is a
couple.
Further,
if the external forces are to be
put
in
equilibrium
by
the addition
of the
anti-resultant of the
effective
forces,
that
is,
by
the
inertia
force for
the
body,
the action
line of
the
resultant
force
must
be determined.
The facts
stated
in
the
following
proposition
are
of
great
importance
in
connection
with the
method
of solution
as outlined above.
Proposition.
If
a
rigid body
rotates about a
fixed axis
through
its
mass-center,
the
resultant
of
the
effective forces
(and
of
the
external
forces
also)
is a
couple
the moment of
which is
equal
to
/a,
the
product
of the moment
of
inertia of
the
body
about
the axis of rotation
and
the
angular
acceleration
of the
body.
If
the
body
rotates
about an axis which does not
pass
through
the
mass
center,
the
resultant of the effective forces
is
a
single
force
having:
a
magnitude equal
to the
product
of the mass
of
the
body
and
the
acceleration
of the
mass-center
of
the
body
(Ma);
a direction
the
same as that
of
the
mass-center;
and an action
line which
does
not
pass through
the mass-center
of
the
body.
For
convenience,
however,
this
single
force
may
be considered
to be
equivalent
to
another
force,
having
an
action
line
which
does
pass
through
the
mass-center,
and
a
couple;
the
magnitude
of the force

SECOND METHOD OF
ANALYSIS
327
is
equal
to
Ma
and
its direction is the same
as that
of
a;
and
the
moment
of the
couple
is
equal
to
la.
The
facts stated
in
the above
proposition, together
with
certain
additional
facts,
are
discussed and
applied
in
the
following
pages,
in
connection
with
the
use of inertia
forces.
It
was found
in
the
preceding
article that
the
expressions
Mra.
and
Mr&
2
represented
the
T-
and
TV-components, respectively,
and
that
IQO.
represented
the
moment,
of
the resultant of the
effective force
system
for the
rotating body.
From these
expressions,
the
resultant of
the
effective forces for various conditions of motion
may
be
determined
completely.
Thus,
it will be noted that
if
f
is
zero
in
these
expres-
sions,
that
is,
if
the distance
from
the
axis
of rotation
to
the mass-
center
of the
body
is
zero,
then each of the
components,
Mra
and
Mru>
2
,
of the resultant of the effective forces is
zero.
Hence,
the
resultant is not a force.
And,
since the
effective forces
have a
moment,
the
value
of which is
loa,
the resultant
is a
couple
of
moment
loot
or
la
since
/o
i's denoted
by
/
when the axis of rotation
passes through
the
mass-center
of
the
body.
The sense of the
resultant
couple
is,
of
course,
the same
as
that of
a,
the
angular
acceleration of the
body. Further,
since the
resultant of the
external forces that act on
the
body
is
identical with that of the
effective forces for the
body,
the
body may
be considered to be
in
equilibrium
if
an additional
couple having
a
magnitude
equal
to
la
and a
sense
opposite
to that of
a
is assumed to act on
the
body
with the external
forces.
This
couple
is
often called
the reversed
effective
couple
or the inertia
couple
for the
body.
If
the
body
rotates about
an axis
which does not
pass
through
its
mass-center,
as indicated
in
Fig.
350,
then
f
in
the above
expressions
is not zero.
The resultant
of
the
effective
forces
for
the
rotating
body,
then,
is a
single
force
since
Mra
and
Mrco
2
express
the
components
of the resultant
force,
the
moment
of
the
resultant
force
(or
of
its
two
components)
being
expressed by
loa.
The action
line of each
of the
two
components
may
now
be
located.
The
action line
of
the
normal
component,
Tlfrco
2
,
of
the resultant
force
lies
along
the line
connecting
the
center of rotation and
the
mass-center of
the
body,
that
is,
along
the
TV-axis
as shown
in
Fig.
350.
This
fact
may
be
proved
as
follows:
Mru
2
was
obtained
by
resolving
the
components
ma
t
and ma
n
,
of the effective
force
for
each
particle,
parallel
to
the TV-axis
and
determining
the
algebraic
sum
of these
TV-components
(Art.
146).
And,
it was
shown

328
FORCE,
MASS,
AND
ACCELERATION
that the
ma
n
components, only,
have an influence
in
determin-
ing
the
magnitude
Mru>
2
since the sum of
the
ma
t
components
was found to be
equal
to zero. Now the ma
n
component
of
the
effective force for each
particle
passes
through
the
center of
rotation.
Therefore,
the
sum,
Mrco
2
,
of their
components
parallel
to the
N-axis must lie
along
the N-axis.
The action
line
of the
tangential
component,
Mr
a,
of
the result-
ant of the
effective forces
may
be found from
the
principle
of
moments; namely,
the moment of the resultant of
the effective
forces
about the
axis of rotation
equals
the
sum of
the
moments
of
the
effective
forces about the same
axis. The sum of
the
moments
w
FIG.
350.
FIG.
351.
of
the
effective
forces,
as
already
shown,
is
IQOL.
Further,
the
moment
of
the
resultant
of the
effective
forces
is
the
moment
of its
tangential
component,
Mra,
only,
since
the
normal
component,
Mrw
2
, passes
through
the
center
of rotation.
Hence,
the
principle
of moments
is
expressed
by
the
equation,
Mra
q
=
loa,
in
which
q
is the
moment
arm
of
Mra
with
respect
to the
center
of
rotation
0,
as
shown
in
Fig.
350.
And,
since
/o
=
M/c
2
,
in
which
k
is
the
radius
of
gyration
of the
body
with
respect
to
the
axis of
rotation,
we
may
write,
Mra
q
=
Mko
2
a
whence,
9
=
T

SECOND
METHOD OF
ANALYSIS
329
Therefore,
the action
lines of the two
components,
Mra
and
Mr
u
2
,
of the resultant
of the effective forces
intersect
in
a
point
on
ko
2
the TV-axis
at a
distance
--
from the center of
rotation,
as shown
in
Fig.
350.
And,
since the
resultant of
the external forces is
identical with
the resultant
of the
effective
forces,
the
body may
be considered
to be
in
equilibrium
if
the two forces
Mra
and
Mru>
2
,
having
the
proper
action lines
as
determined above
and shown
in
Fig.
350,
but reversed
in
sense,
are assumed to act on
the
body
with the
external
forces.
The
component
Mru>
2
of
the inertia
force
is sometimes
called the
centrifugal
force.
However,
instead
of
determining
the resultant
of the effective
forces
as a
single
force
(or
as
components
of a
single
force)
as
was
done
above,
it is
usually
more convenient
to find the resultant
of
the effective forces
as an
equivalent
force
and
couple;
the
force
having
components
equal
to
Mra
and
Mru>
2
parallel,
respectively,
to
the
T- and
TV-axes,
as
before,
but
with action lines
passing
through
the mass-center
of the
body.
The
fact
that the
compo-
nents
of this
new force
are the same
in
magnitude
and
sense as those
of
the
single
resultant
force,
follows
from
Art.
18,
in
which the
resolution
of
a force
into
a force
and a
couple
is discussed.
The
fact
that the moment of the
couple, C,
is
equal
to
la
may
be
proved
as
follows:
The
moment
of
the effective forces about the axis of
rotation
is
loa
as
already proved.
And,
if
the resultant
of
the
effective forces is a
force
having components
Mra
and
Mrco
2
acting through
the
mass-center,
and a
couple
the moment of
which is
represented
by
C,
as stated
above,
then,
the
principle
of
moments
is
expressed
by
the
equation,
But,
I
Q
=
J+Mr*
(Art.
102).
Hence,
C
=
Ia.
Therefore,
a
rigid
body (Fig. 351)
rotating
about
a
fixed
axis
under the
action of an
unbalanced force
system (P, W,
and
the
reaction of
the
axis at
0)
may
be
considered to be
in
equilibrium
if
an
additional force and
couple
are
assumed to act on the
body
with
the
external forces.
The
additional inertia
force
must act
through
the mass-center
of
the
body;
it
must have
components

330
FORCE, MASS,
AND
ACCELERATION
equal
to
Mra
and
Mrco
2
,
the directions
of
which
are
parallel
respectively
to the
T- and
A^-axes;
and the
senses of
the com-
ponents
must
be
opposite
to those of
the
corresponding components
of acceleration of
the
mass-center,
as shown
in
Fig.
351. The
additional inertia
couple
must have a
moment
equal
to
la
and
must have a sense
of rotation
opposite
to that of the
angular
accel-
eration,
a,
of the
body,
as
shown
in
Fig.
351. The forces of the
couple,
of
course,
may
be assumed to
act
anywhere
in
the
plane
of
motion of
the
body,
provided
that the
moment
of the
couple
remains constant
(Art. 27).
ILLUSTRATIVE
PROBLEMS
376.
A
horizontal
bar
B
(Fig. 352,
a)
rotates
with
a
constant
angular
velocity
of
45
r.p.m.
about a
vertical axis
YY.
A
slender
rod
C,
of
constant
cross-section,
having
a
length
of
12
in.
and
a
weight
of
16
Ib.
is
attached to
the
rotating
bar
by
means
of
a smooth
pin
at
E,
and
is
held in
a
vertical
position
by
a
weightless
cord
D.
Find the
tension in D
and
the
magnitude
of
the
reaction of
the
pin
at
E
on
the
rod C.
Solution.
A
free-body
dia-
gram
of
the
rod C is
shown in
Fig.
352,
6.
The rod has a
mo-
tion of
rotation
about
the
vertical
axis
YY under the influence
of
three forces
W,
D,
and the
pin
pressure
at
E
(the
components
of the
pin
pressure
being
denoted
by
E
x
and
E
v).
10
T
TE
