Seely F.B. Analytical Mechanics for Engineers
Подождите немного. Документ загружается.


LIMITATIONS
OF MOMENT
EQUATION
T
=
Ia
351
rod is
30 in.
long
and
weighs
83
Ib
,
what is
the linear acceleration
of the
mass-center of the rod
and
the
angular
acceleration
of
the
rod, assuming
the rod
to be
of constant
cross-section?
FIG. 372.
151.
Limitations
of
the
Moment
Equation
T
=
Ia.
As
dis-
cussed
in Art.
134,
a
rigid
body
having plane
motion
may
be
given
its
actual
motion,
at
any
instant, by
a
combination
of a
rotation
and
a translation.
And,
it
was
shown
that
in
giving
the
body
the
rotational
motion,
the axis about which the
body
is
assumed to
rotate
may
be
any
axis, 0,
in the
body,
perpendicular
to
the
plane
of
motion,
the
corresponding
translation
of the
body being
defined
by
the motion which
the
arbitrarily
chosen
axis,
0,
has
at
the
instant.
It does not
follow,
however,
that the
resultant
external
force
which
is
required
to
produce
the
translation
is
the
product
of
the mass of the
body
and
the
translatory
accelera-
tion, ooj
which
each
particle
receives,
as is the case for a
body
for
which
the actual
(or sole)
motion is translation
(Art.
145).
Nor
does
it
follow
that the moment
of the resultant of
the external
forces which
is
required
to
produce
the rotational
part
of the
motion
is
the
product
of the moment
of
inertia, /o,
of
the
body
about
the
arbitrarily
chosen
axis and
the
angular acceleration,
a,
of
the
body,
as is
the
case for a
body
for
which
the actual
(or
sole)
motion is rotation
(Art.
146).
Equations
(1)
of Art.
149 show
that
the
resultant
force
required
to
produce
the
translatory part
of
a
plane
motion is
the
product
of
the
mass
of the
body
and the
translatory
acceleration, only
when
the axis
is
chosen
through
the
mass-center of
the
body,
that
is,
when
x
and
y
in
equations
(1)
are
zero. The
simple
moment
equation,
To
=
/oa,
also
applies
to a
rigid
body
having
a
plane
motion when
the
arbitrarily
chosen
axis,
0,
passes through
the
mass-center
of
the
body,
as
was
also
shown
in
Art. 149.
It
also
applies,
however,
for two
other
positions
of
the
axis
0,

352
FORCE,
MASS,
AND ACCELERATION
as stated
under
(3)
and
(4)
below.
Thus,
in
considering
a
plane
motion
of a
rigid body
under the action of
an
unbalanced
force
system,
the moment of the
resultant of
the external
forces about
an
axis
in
the
body
is
equal
to the
product
of
the moment
of inertia
of
the
body
with
respect
to the same axis
and
the
angular
accelera-
tion
of
the
body
only
when
one
(or
more)
of the
following
four
conditions are
satisfied,
the first of which restricts
the
motion
of
the
body
to a
special
case
of
plane
motion
(rotation)
and
the
other three
restrict
the
choice of the axis
in
the
body,
about
which
the
rotational
part
of
the
motion is assumed to take
place
:
1.
If
the
body
rotates about
an axis
which
is
fixed
in
space
as well
as
in
the
body,
then
OQ,
in
equations
(1)
of
Art.
149,
is
zero
and
hence
the moment
equation
reduces
to
TO
=
/O.
This restriction
on the
axis limits the motion to
pure
rotation,
which
is
treated
in Art. 146 and
is,
of
course,
a
special
case of
plane
motion.
2.
If the
arbitrarily
chosen
axis
in
the
body,
about
which
moments
are
taken,
passes through
the mass-center of
the
body,
then
x
and
y
in
equations
(1)
are zero and the moment
equation
reduces
to
T=Ia
as
discussed
above.
3.
If
the acceleration of the
point
(in
the
plane
of
motion)
through
which
the moment axis is
taken,
is directed
toward
the
mass-center
of the
body,
then,
the
quantity
[M(ao)
x
y
M(ao)yx]
in the
expression
for the
moment,
in
equations
(1),
is
zero
and
hence
the moment
equation
reduces to
TQ
=
IQCX.
The
quantity
[M(ao)
x
y
M(ao)v
x]
is the moment of the force
Mao
with
respect
to the
mass-center of the
body,
and
if
OQ
passes
through
the
mass-center,
then
Mao
also
passes through
the
mass-center
and hence
its moment with
respect
to the
mass-center
is
zero.
4.
If the
arbitrarily
chosen axis
in
the
body,
about which
moments
are
taken,
passes
through
the instantaneous center
of zero
acceleration
(not
the instantaneous
center of
zero
velocity,
Art.
135)
then
OQ
in
equations
(1)
is
zero
and
the
moment
equation
reduces
to
TQ
=
loa.
The
location of the
arbitrarily
chosen axis
as
required
under
(3)'
and
(4)
above is of considerable
importance
in
the
study
of
certain
problems
in
Dynamics
of
Machinery,
a detailed
discussion
of which
is
beyond
the
scope
of this book.

PRINCIPLE OF MOTION OF MASS-CENTER 353
PROBLEM
399. Solve
Prob.
385
by
use
of the
equations;
2F
x
=
Ma
x
,
2F
v
=
Ma
v
,
and
"2TA=lA<*,
in
which
moments are taken about an axis
through
A,
the
point
of contact
of the
cylinder
with
the
inclined
plane.
Does the
moment
equa-
tion
^TA=IAOC
apply
for this
position
of the
moment axis because A
is the
point
about which the
body
is
rotating
at the instant
(instantaneous
center of
zero
velocity)?
If
not,
which
one of the
four
special
cases
stated above
applies
when
the moment axis
passes
through
A?
152.
Principle
of the Motion of the Mass-Center. For
each
of the three
types
of
motion
of
rigid
bodies
(translation,
rotation,
and
plane
motion) already
discussed
in
this
section,
there are three
equations
of
motion. The
first
two
of each
of these
sets of
-equations
((2)
of Art.
145;
(1)
of Art.
146;
and
(2)
of
Art.
149)
may
be
written so as to
apply
to
all three
types
of motion.
The
equations
are,
2F
X
=
Max
and
2F
v
in
which
x and
y
denote
any
two axes at
right
angles
to each other.
Thus,
for the motion of translation of a
rigid
body,
a
x
and
a
v
are
the
same as the
a
x
and
a
v
of
any
other
point
in
the
body
and
hence,
in
equations
(2)
of
Art.
145,
a
x
=
a
x
and
a
v
=
a
v
-
For the motion of
rotation of a
rigid body
the
T-
and TV-axes were
chosen and
in
the
equations
(1)
of
Art
146,
ra
=
at
and
ru
2
=
a
n
-
For
plane
motion
of
a
rigid body
the first
two of
equations
(2)
of
Art.
149 are
already
in
the
form
written
above.
However,
these two
equations
are
not
restricted
to the
motion
of
rigid
bodies
having
the
three
types
of
motion treated in
the
preceding
articles.
They
apply
to
any
mass-system having any type
of motion.
,
They
express
mathe-
matically
a
principle
which is called the
principle
of
the motion
of
the mass-center. The extension
of the
proof
of
this
principle
to
any
motion
of
any
mass-system
involves
the
same fundamental
laws and the same methods as were used
in
the
preceding
articles
in
deriving
the
equations
of
motion
for
a
rigid
body
having
the
three
special types
of motion. The
principle
of
the motion of
the mass-center
may
be stated
in
words
as
follows:
If
an
unbalanced
external
force
system
acts
on
a
body
(whether
rigid
or
not),
the
resultant
of
the external
force
system,
if a
force,
has
a
magnitude
which is
equal
to
the
product
^of the
mass
of
the
body
and the acceleration of tte

354
FORCE,
MASS,
AND
ACCELERATION
mass-center
of
the
body,
and
the
direction
of
the
resultant
force
is the same
as that
of
the
acceleration
of
the
mass-center.
Likewise,
the
component,
in
any
direction,
of
the
resultant
of
the
external forces is
equal
to
the
product
of
the
mass
of
the
body
and the
component
of
the
acceleration of
the
mass-center in
the
given
direction.
The
statement of the
principle
as
given
above
is
in
the form
which
makes it
most
directly
applicable
to
the
method of
analysis
which
reduces
the
kinetics
problem
to an
equivalent
statics
prob-
lem
by
introducing
inertia
forces.
The
principle
may
also
be
stated
in
the
following
form
:
The
algebraic
sum of
the
components,
in
any direction,
of the external
forces
which act
on
any
mass-system
is
equal
to the mass of
the
whole
body
times the
component,
in
the
given
direction,
of
the
acceleration of
the
mass-center of
the
mass
system.
It will be noted
that,
according
to
the
principle
of the
motion
of the
mass-center,
the
mass-system
or
body
may
be
assumed
to be reduced to a
particle
having
a
mass which
is
equal
to
the
total
mass of the
body
and
which is
located
at,
and
moving
with,
the
mass-center of the
body.
That
is,
the
magnitude
and
direction of
the
resultant of the actual
(non-concurrent)
forces
which act on
the
actual
body
are the
same as the
magnitude
and
direction of
the
resultant of the
(concurrent)
forces which
would
have to act on
the
mass
if
it
were concentrated
at,
and
moving
with,
the mass-
center of
the
body.
It
is
important
to
note,
however,
that
the action
line of the
resultant of
the forces
acting
on a
body,
does
not,
in
general, pass
through
the mass-center
of
the
body
whereas it
would
necessarily
do so if
the
mass of the
body
were
actually
concentrated
at
the
mass-center.
Further,
the
principle
cannot be
used to determine
the
resultant of
the forces
acting
on
a
body
when the resultant is
a
couple.
Nevertheless,
the
principle
simplifies
many problems
and
is
of much
importance
in
the
study
of
kinetics.

PRINCIPLE
OF MOTION
OF
MASS-CENTER
J355
ILLUSTRATIVE PROBLEM
400.
Two bodies A and
B
(Fig.
373)
are
connected
by
a
light
slender rod
and
revolve
in a horizontal
plane
about a,n axle
fixed in
the
top
of a vertical
post
which
supports
the
two bodies.
Body
A
weighs
4
Ib. and
B
weighs
12
Ib.
The
bodies
rotate with
an
angular
velocity
of
80
r.p.m.
What
horizontal
force acts
on
the
post
tending
to
bend
the
post?
The mass of the
rod
may
be
neglected.
Solution.
The mass-center
of the
two
bodies
is found
by
the
principle
FIG.
373.
of moments
to be at a
distance
r
=
5 in.
from the axis
of
rotation.
The acceleration
of
the
mass-center
is,
ft./sec.*,
directed
toward the
center
of rotation. The resultant
force
acting
on the
two bodies
is,
44-12
Ma
n
=
^-
--X29.2
=
14.51b.
oZi.Zi
This force is exerted
on the two bodies
by
the
post,
and the two
bodies exert an
equal
and
opposite
force
on the
post. (Check
the answer
by finding
the force
acting
on
each
body
and
subtracting
one force from
the
other.)
PROBLEMS
401.
A solid wooden
disc
10
ft.
in diameter rotates in
a
horizontal
plane
about
its
geometric
axis. Two small bodies each
weighing
50
Ib. are
attached
to
the disc
at a
radius of
4 ft. from the axis of rotation
so that
the
radii
make
an
angle
of 90.
If the disc
rotates at 40
r.p.m.
what is the
resultant
horizontal
pull
on the
axis? Solve
by
two
methods, Ans.
154
Ib.
402.
A
flat-topped
boat
having
a
weight
of
300
Ib. and a
length
of
12
ft.
is
resting
in
still water.
A man
weighing
150
Ib.
stands
at
one end of
the
boat.
The
man starts
to
run with a
speed increasing
at
the rate
of
10
ft.
per
sec.
each
second.
When
he
reaches the other end
of
the
boat
he
jumps.
Assuming
that the
water
is
a
perfect
(frictionless)
fluid
what
is
the
acceleration
of the
mass-center
of
the
boat and man
(considered
as
one
body)
before the
man
starts
to
run?
While
he is
running
on
the
boat?
After
he
jumps
from
the
boat but
before
he strikes
the water?
What
is
the
acceleration
of the
boat
while the man
is
running
on
it?
403.
Two
bodies
A and
B
(Fig.
374),
each
weighing
8
Ib.,
are connected
by
a
string.
Body
A
is
placed
on a
smooth
table
and
the
other
body
B is sus-
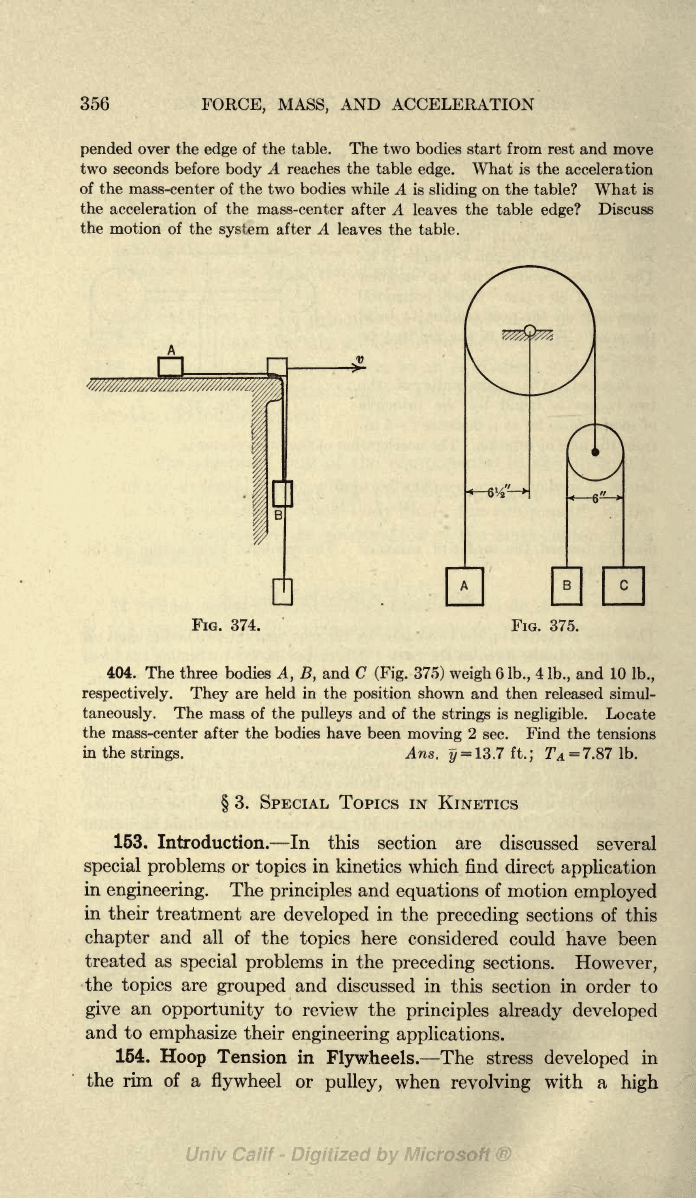
356
FORCE, MASS,
AND ACCELERATION
pended
over the
edge
of the table.
The two
bodies start from rest and
move
two seconds before
body
A reaches
the
table
edge.
What is the acceleration
of the
mass-center
of the
two bodies
while A
is
sliding
on the table?
What
is
the
acceleration of
the mass-center
after
A leaves
the
table
edge?
Discuss
the motion
of
the
system
after A leaves
the
table.
FIG.
374.
FIG. 375.
404.
The
three bodies
A, B,
and
C
(Fig.
375)
weigh
6
lb.,
4
lb.,
and
10
lb.,
respectively.
They
are
held in the
position
shown and then released
simul-
taneously.
The mass
of
the
pulleys
and of
the
strings
is
negligible.
Locate
the
mass-center after the bodies have
been
moving
2
sec.
Find
the
tensions
in the
strings.
Ans.
y
=
l3.7
ft.;
7^
=
7.87 lb.
3. SPECIAL
TOPICS
IN
KINETICS
153.
Introduction. In
this
section
are
discussed
several
special
problems
or
topics
in
kinetics
which find
direct
application
in
engineering.
The
principles
and
equations
of
motion
employed
in
their
treatment
are
developed
in
the
preceding
sections of this
chapter
and all
of
the
topics
here
considered
could have been
treated as
special
problems
in
the
preceding
sections.
However,
the
topics
are
grouped
and
discussed in
this
section
in
order to
give
an
opportunity
to review
the
principles already developed
and to
emphasize
their
engineering
applications.
154.
Hoop
Tension in
Flywheels.
The
stress
developed
in
the rim of a
flywheel
or
pulley,
when
revolving
with a
high

HOOP
TENSION IN FLYWHEELS 357
angular
velocity,
is
sometimes of considerable
importance.
Likewise
the stress
developed
in
a
belt,
due to
the same
cause,
as
it
passes
around a
flywheel
or
pulley,
must
sometimes be con-
sidered.
If
the tension
in
the
spokes
of a
flywheel
is
neg-
lected,
the
tensile stress
in
the
rim
(often
called
hoop
tension)
corresponding
to an
angular velocity,
co,
may
be
found as
follows:
In
Fig.
376
is
represented
one-half of
the
rim
of a
flywheel.
As the
wheel
rotates,
each half of
the
rim
tends to
separate
from
the other
half
and is
prevented
from
doing
so
by
the stresses
JTIG 375.
P,
P
which are
developed
in
the
rim.
The
reversed effective
force for
the
half of the
rim
is
Mrco
2
and it
acts
through
the
mass-center
of the
half-rim.
And,
since the
reversed
effective force
(inertia
force)
is
in
equilibrium
with
the
external
forces
(P, P)
which
act
on
the
half-rim,
the
following
equation
of
equilibrium
may
be
written,
W
ru
2
,
in
which
W
is
the
weight
of the half-rim.
Now
if the thickness
of
the
rim is
small
in
comparison
with the mean
radius
r,
the
mass-
center of the rim
may
be
considered to
coincide with
the centroid
2r
of
the
semicircular
arc,
and
hence
r
=
(Art. 82).
7T
Whence,
2-
X
co
=
2
Q
TT
TFrco
2
-
.
gir
The
stress, s,
per
unit
of area of
the rim
cross-section
is
P
in
which
a
is the area
of
the
cross-section.
Therefore,
_W
r co
2
_7rmfc
r
co
2
_kr
2
co
2
"
X
/N.
/\
/\
,
g
TT
a
g
TT
a
g

358
FORCE, MASS,
AND
ACCELERATION
in
which
k
is the
weight
of the material
per
unit volume.
Or,
since
the
velocity, v,
of
the
mid-points
of
the rim
is
equal
to
cor,
the
expression
for
s
may
be written
in
the
form,
kv
2
The
units
in
which
s
is
expressed
are
Ib.
per
sq.
ft.
if k
is
expressed
in
Ib.
per
cu.
ft.,
r in
ft.,
g
in
ft.
per
sec.
2
,
and
xo
in
rad.
per
sec.
It
will be
noted,
therefore,
that the
intensity
of
stress, s,
developed
in the rim of a
rotating
wheel,
if
the rim is thin
and
the
effect of
the
spokes
is
neglected,
varies
directly
as the
square
of
the
linear
speed
of the rim.
PROBLEMS
405. A common rule limits the
peripheral speed
of cast-iron
flywheels
or
pulleys
to 6000 ft.
per
min.
(Sometimes
stated one mile
per minute.)
Cal-
culate the tensile unit-stress in the rim
corresponding
to
this
speed, assuming
that
the effect
of the
spokes may
be
neglected.
Ans.
970
Ib.
per
sq.
in.
406.
Calculate
the
greatest
number of
revolutions
per
minute
(r.p.m.)
at which a
thin
cast-iron
hoop
can rotate without
Bursting.
Assume that the
maximum tensile
strength
of
the cast
iron
is
20,000
Ib.
per
square
inch,
that
the
material
weighs
450
Ib.
per
cubic
foot, and
that the
radius is
2 ft.
*
155.
Superelevation
of Railroad
Track. The
wheels of
a
locomotive,
electric
car,
etc.,
when
traveling
round a
curve of
radius,
r,
on a
level track exert
a horizontal
thrust,
H
(flange pres-
sure),
on the
outer rail as
shown
in
Fig.
377
(a).
The
reversed
Q
effective
force,
Mru
2
or
M-
,
if
acting
on the car
with the
four
external forces
Ri, R2, H,
and
W,
would
hold
the
car in
equilibrium.
Hence Mrco
2
and
H
form
a
couple
the moment of
which,
for
a
given
car
and
radius
of
curvature, depends
both
upon
the
speed
of
the
car and
the
height
of the center of
gravity, G,
above
the
rails. In
order to
reduce the
magnitude
of the horizontal thrust and
of
the
overturning
couple,
the
outer
rail is
elevated
above the
inner
rail
a
distance,
e,
which
is called
the
superelevation.
It
is
desired to
determine the
superelevation
required
to reduce
the
flange pressure
to zero for a
given
speed
of the
car and curva-
ture
of the
track.
Thus,
in
Fig.
377(6),
the
pressures
of
the rails
are
RI
and
R2,
the
resultant of
which
is
R;
W
is
the
weight
of the
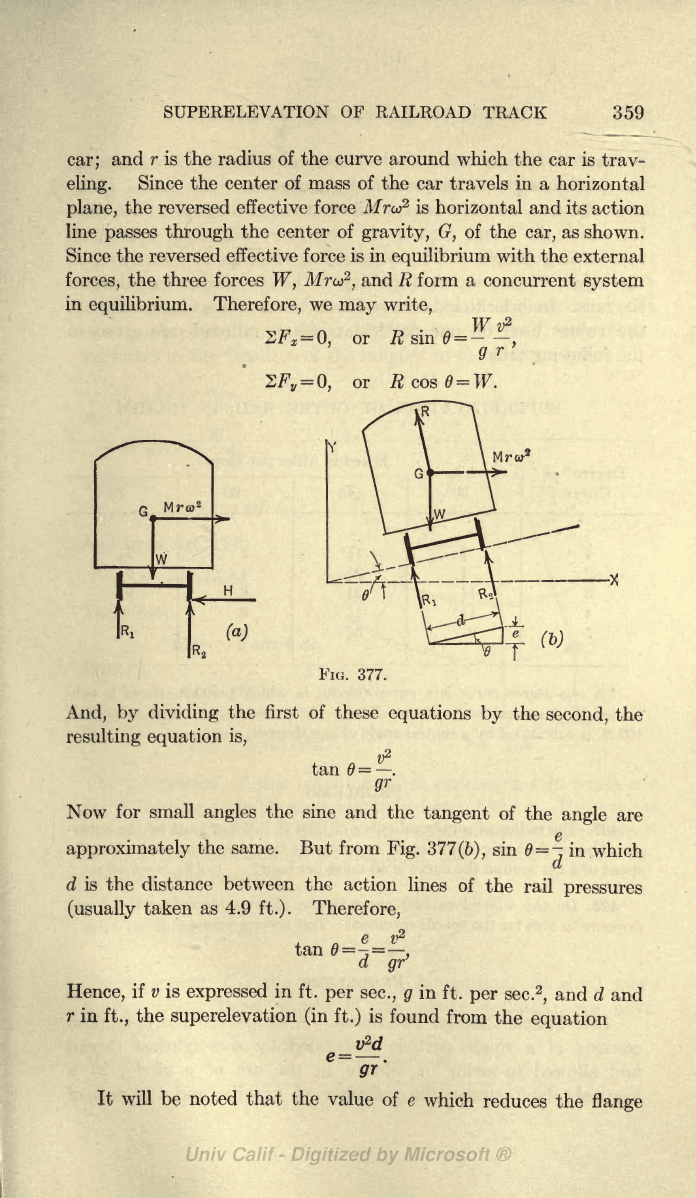
SUPERELEVATION
OF
RAILROAD
TRACK
359
car;
and
r is the radius of the curve
around
which the
car is
trav-
eling.
Since the
center of mass of
the car
travels
in
a
horizontal
plane,
the reversed effective force
Mrco
2
is horizontal
and its
action
line
passes
through
the
center of
gravity,
G,
of
the
car,
as
shown.
Since the
reversed effective force is
in
equilibrium
with
the external
forces,
the three forces
W,
Mrw
2
,
and R form a
concurrent
system
in
equilibrium.
Therefore,
we
may
write,
W v
2
2/^
=
0,
or
Rsm
=
,
Mror
W
(a)
FIG.
377.
And, by dividing
the first of
these
equations
by
the
second,
the
resulting
equation
is,
tan
=
-.
gr
Now
for small
angles
the
sine and
the
tangent
of
the
angle
are
o
approximately
the
same.
But
from
Fig.
377(6),
sin
=
-
in
which
d
d is the distance
between
the action
lines
of
the
rail
pressures
(usually
taken
as 4.9
ft.).
Therefore,
tan
0=^
=
,
d
gr'
Hence,
if
v
is
expressed
in
ft.
per
sec.,
g
in
ft.
per
sec.
2
,
and d
and
r
in
ft.,
the
superelevation
(in
ft.)
is
found
from
the
equation
v
2
d
It
will
be
noted that
the
value
of
e
which
reduces the
flange

360
FORCE, MASS,
AND
ACCELERATION
pressure
to zero also
reduces the
overturning
couple
to
zero
regard-
less
of the
height
of
the center of
gravity
above the
rails.
How-
ever,
if a car
travels
round a
curve
at a
speed
greater
than
that
for which the
flange
pressure
is
zero,
there
will
be,
of
course,
an
overturning
couple
and its
magnitude
will
depend
directly upon
the
height
of the center
of
gravity
of
the car
and
its
cargo
above
the rails.
In order to
indicate common
values of
the
superelevation,
the
values
used on one
particular
steam
railroad
are
given
in
the
following
table :
SUPERELEVATION
OF
OUTER RAIL
IN
INCHES
Degree
*
of
