Seely F.B. Analytical Mechanics for Engineers
Подождите немного. Документ загружается.


SECOND METHOD OF
ANALYSIS
ZF
X
=22E
x
D
cos 45
=
331
cos
45=0
The solution
of
these
equations gives
the
following
results:
D
=20.71b.
E
x
=
7.331b.,
E
v
=
1.33\b.,
#
=
7.451b.
376. A bar
B,
2
in.
by
6 in.
by
4
ft.,
is
attached
to a
cylindrical
disc,
A,
by
means
of two
steel
straps,
D
and
E,
as shown
in
Fig.
353
(a).
The
cylin-
drical disc is
keyed
to a shaft
which
causes the disc and
the bar to
rotate in
a
vertical
plane.
When
the
bar
is in a
horizontal
position
as
shown,
the
angular
velocity, co,
of the shaft is 30
r.p.m.
and it
is
decreasing,
at the
instant,
at the
rate of 120
r.p.m. per
sec.
The
weight
of the
bar
is 96 Ib. The
diameter of
the disc
is 18 in. and that
of the
shaft
is 4
in. The
straps,
D
and
E,
are
attached
to the bar
by
means
of smooth
pins.
Find
(a)
the
torque
transmitted from
the shaft to
the bar
B,
(6)
the
sum of the
pin pressures
in
the
horizontal
direction,
and
(c)
the
sum of the
pin
pressures
hi
the
vertical
direction.
to
.

332
FORCE,
MASS,
AND ACCELERATION
Thus,
the
force
system
acting
on the bar is a non-concurrent
system
in
a
plane,
the
equations
of
equilibrium
for which
are,
2^
=
0,
H-
80.8
=
0,
2F
V
=
Q,
103-7-96
=
0,
ZM
G
=
0,
-C+50.0+2F
=
0.
Solving
these
equations
we
obtain,
tf
=
80.81b.,
7
=
7.01b.,
C
=
641b.-ft.
The
magnitude
of each
of the
forces
that form the
couple, C,
depends
on
the
distance
between
the
pins.
If
this distance is 3
in.,
then
each force
is
256 Ib.
PROBLEMS
377.
Solve
Prob.
376
by introducing
a
single
force as the reversed
resultant
of
the
effective
forces instead of
introducing
a reversed force and
couple.
378. A
small
body
is
placed
on a
rough
horizontal disc which
rotates about
a vertical
axis.
If the
distance of the
body
from the axis
is
9 in.
and the
coefficient
of
friction
between the
body
and disc
is
f,
find
(1)
the
greatest
ang
ilar
velocity
and
(2)
the
greatest
angular
acceleration
the disc can have
without
causing
the
body
to
slide. Ans.
u>=51
r.p.m
;
a
=28.
5
rad./sec.
2
379.
A
flywheel
used on
a
punching
machine
is
8
ft. in diameter and has a
rim
which
weighs
1
ton. Each
operation
of
punching
a hole causes the
speed
of the
flywheel
to decrease
uniformly
from
100
r.p.m.
to 80
r.p.m.
The
fly-
wheel
has 6
spokes,
each 3.5
ft.
long.
If
the
time of
punching
a
hole is 0.5
sec.,
what
moment is transmitted
from
the
rim
to
the hub
by
each
spoke.
Assume
that the
thickness
of the
rim is small
in
comparison
with
the radius of
the
fly-
wheel
and
neglect
the
weight
of the
hub
and
spokes.
Ans.
607
Ib.-ft.
380. A uniform bar AB and
a
mem-
ber
C,
to which
AB
is
pinned
at
A
(Fig.
354),
rotate,
at a
speed
of 40
r.p.m.
about
a
vertical axis.
The
weight
of
the
bar
is 40 Ib. and its
length
is
4
ft.
If
the bar is
connected
to the
axis
by
a
FIG. 354.
spring
S
(assumed horizontal),
as shown
CENTER
OF
PERCUSSION 333
in
the
figure,
find the
pull
of
the
spring
and the horizontal and vertical
components
of
the
pin
pressure
at A.
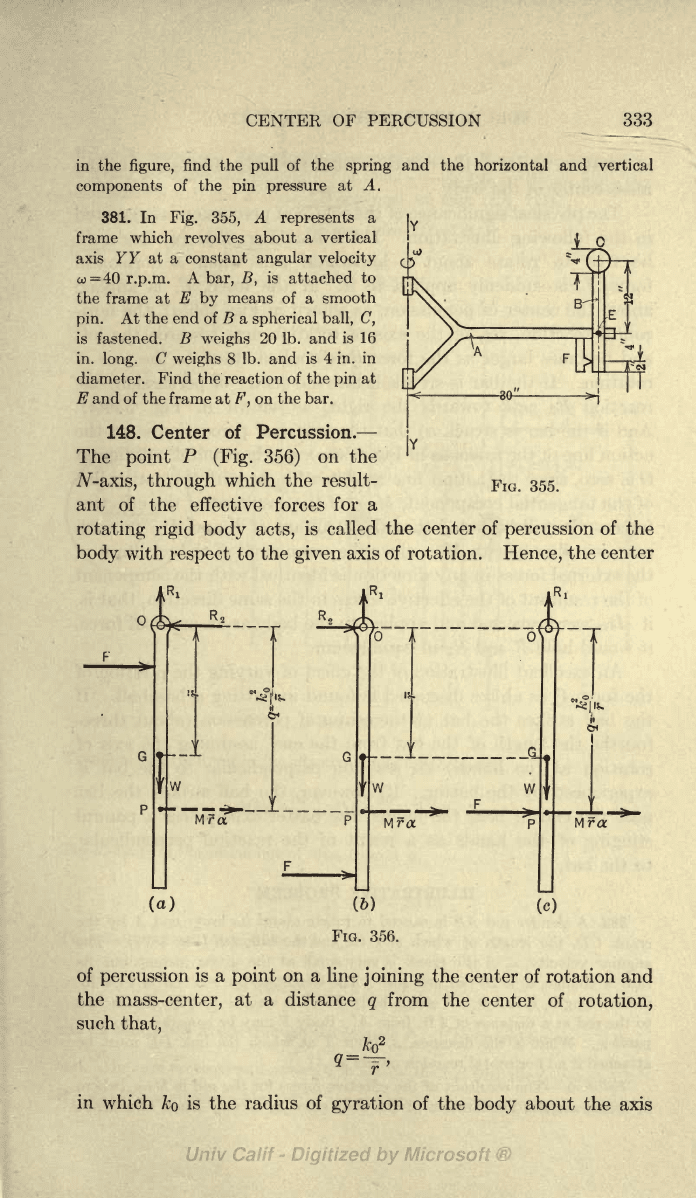
381. In
Fig. 355,
A
represents
a
frame which revolves
about a vertical
axis YY at a constant
angular velocity
co =40
r.p.m.
A
bar,
B,
is attached
to
the frame at
E
by
means of a
smooth
pin.
At
the end
of B
a
spherical
ball, C,
is fastened.
B
weighs
20
Ib. and
is 16
in.
long.
C
weighs
8
Ib.
and
is
4 in. in
diameter.
Find the reaction
of the
pin
at
E
and of the frame at
F,
on
the
bar.
148. Center
of Percussion.
The
point
P
(Fig.
356)
on
the
|Y
./V-axis,
through
which the result-
JTIG
355
ant
of
the effective
forces
for a
rotating rigid
body
acts,
is called
the center of
percussion
of the
body
with
respect
to
the
given
axis of rotation.
Hence,
the
center
i:
Mr
a
of
percussion
is a
point
on
a
line
joining
the center of
rotation and
the
mass-center,
at a
distance
q
from
the center
of
rotation,
such
that,
in
which
ko
is the radius
of
gyration
of
the
body
about the
axis

334
FORCE, MASS,
AND
ACCELERATION
of rotation and
r
is
the
distance from the axis of
rotation
to
the
mass-center
of
the
body.
The
physical significance
of
the center of
percussion
is
suggested
in the
following
illustration.
Let
a
bar
(Fig.
356)
of
weight
W
be
free
to rotate about a horizontal
axis
when a
horizontal
force,
F,
is
suddenly applied
to it. If
the
force,
F,
is
applied
above the
center of
percussion,
as
shown
in
Fig.
356
(a),
the hori-
zontal
reaction, #2,
of the axis of
rotation
acts
towards
the left
and becomes
larger
as
the force
F is
applied
closer
to
the axis
of
rotation.
If the bar is struck
below the
center of
percussion,
the
reaction
RZ
acts
towards the
right,
as
shown
in
Fig. 356(6).
And
if
the bar
is struck so that
the center of
percussion
is
on the
action
line
of the
force,
as
in
Fig.
356(c),
the horizontal
reaction at
is
zero,
since the
action
line at
F
is collinear
with
the action
line
of
the
tangential
component, Mfa,
of the
resultant
of the
effective
forces.
It will
be
noted that the
resultant of
F
and
/fo,
in
each
case,
is collinear with
Mr
a
,
since the
component
of
the
resultant of
the
external
forces
in
any
direction is
identical with
the
component
of the resultant
of
the effective forces
in
the
same
direction,
that
is,
if
Mra
were
reversed and
applied
to the
body
as an
external
force,
it
would
hold
F
and
R%
in
equilibrium.
An excellent illustration of the effect of
varying
the
position
of
the force
F
as above discussed is found
in
batting
a
baseball. If
the
ball strikes the bat at the center of
percussion
(about
three-
fourths
the
length
of the bat from the
end,
assuming
the
axis of
rotation
at
the
hands)
no
reaction
perpendicular
to
the
bat is
experienced
by
the batter.
If, however,
the
ball
strikes the
bat
near the
end or
near the
hands,
the batter
experiences
a
painful
stinging
of
the
hands as a result of the
reaction
perpendicular
to the bat.
ILLUSTRATIVE
PROBLEM
382.
A slender
rod
AB
is caused to rotate about its
lower end A
by
the
crank
CD,
the
length
of
which
is
1
ft.,
and
the
link
DE
(Fig.
357
a).
The
angular velocity, o>,
of the crank is
very
small
at the
given
instant
but
its
rate of
change, a,
is 20 rad.
per
sec.
2
The
weight
of the rod
AB
is
64.4
Ib.
and its
length, I,
is 5 ft. A small
body
F
which
weighs
16.1
Ib.
is
attached
to
the
rod at
a distance
of
2
ft. from A.
Body
F
may
be
considered to be a
particle.
What
is the
distance, d,
from A
at which
the link DE
must
be
attached
if no horizontal reaction
occurs at
A?
Solution.
The resultant of
the effective forces for
the rod
is
Mra\
(where
a\
is
the
angular
acceleration of the
rod)
since
on
is
very
small
and
hence
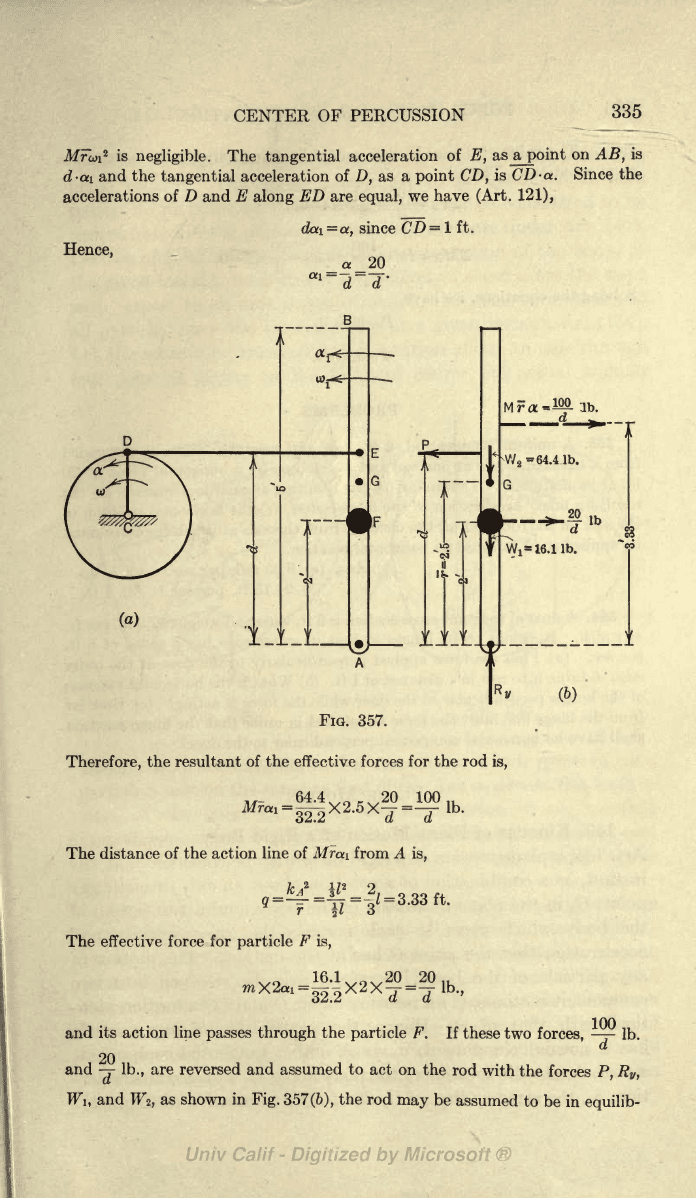
CENTER
OF PERCUSSION
335
Afrcoi
2
is
negligible.
The
tangential
acceleration
of
E,
as
a
point
on
AB,
is
d-ai
and
the
tangential
acceleration
of
D,
as
a
point
CD,
is CD
-a.
Since the
accelerations
of
D
and
E
along
.EJD are
equal,
we
have
(Art.
121),
Hence,
i
=a,
since CD
=
1 ft.
a
20
(a)
FIG.
357.
Therefore,
the resultant
of the
effective
forces for the rod
is,
The
distance
of the action
line of
Mfai
from A
is,
The effective
force
for
particle
F
is,
and
its action line
passes through
the
particle
F. If
these two
forces,
7-
Ib.
a
20
and
Ib.,
are
reversed and assumed
to act
on
the
rod
with
the
forces
P,
R
v
,
Wi,
and
Wz,
as
shown
in
Fig. 357(6),
the rod
may
be
assumed
to
be in
equilib-

336
FORCE,
MASS,
AND
ACCELERATION
rium.
The
value of
d
may
be determined
by using
only
two of
the
equilib-
rium
equations. Thus,
Solving
the
equations,
we
have,
P
=
38.61b.,
d
=
3.11 ft.
PROBLEMS
383.
A
uniform slender
rod,
6 ft.
long
and
weighing
20
lb.,
is
suspended
from
a horizontal axis at one end and is
acted
on
by
a horizontal
force of
20
lb. at
its
mid-point.
Determine
(a)
the
resulting angular
acceleration,
(6)
the
resulting
linear acceleration
of the
mass-center, (c)
the
horizontal
reaction of
the axis
on
the
rod,
and
(d)
the distance
from the
axis at
which
the
force must
be
applied
so as
to cause no
horizontal reaction.
Ans.
(a)
8.05
rad.
per
sec.
2
(c)
5 lb.
(6)
24.15
ft.
per
sec.
2
(d)
4
ft.
384.
A
door of constant cross-section
is
3
ft. wide
and
weighs
32.2
lb.
per
ft.
of width.
It
swings
on its
hinges
so that its outer
edge
has
a
speed
of
8 ft.
per
sec.
(a)
Find the force
applied perpendicularly
to the door
at the
outer
edge
to
.bring
it
to
rest in
a distance of
1 ft.
(6)
What is the
horizontal reaction
of the
hinges perpendicular
to the door while the force is
acting?
(c)
How
far
from
the
hinge
line
must the
force
be
applied
in order that the
hinge
reaction
shall
have
no horizontal
component perpendicular
to
the
door?
PLANE
MOTION
149.
Kinetics of Plane Motion of a
Rigid Body.
As
shown
in
Art.
134,
a
plane
motion of a
rigid body may
be
considered,
at
any
instant,
as
a
combination
of
a rotation about an axis
through any
point, 0,
in
the
plane
of motion of the
body,
and
a translation of
the
body
which
gives
to
each
particle
the same
velocity
and
acceleration
that the
point
has at the instant. The
motion
of
any particle
of the
body,
therefore,
may
be resolved into
two
component
motions, (1)
a
rotation
about and
(2)
a
motion
iden-
tical
with
that of
0.
Hence,
the acceleration
of
any
particle
has a normal
component,
a
n
=
ru>
2
,
and a
tangential
component,
Ot
=
ra,
due to
the
rotation
of the
body
about
0,
and
also an
acceler-
tion, OQ,
the
same
as
that
of
0,
due
to the translation
of the
body.

KINETICS OF
PLANE MOTION OF
RIGID BODY
337
Thus,
in
Fig.
358,
let the
diagram represent
a
body
which
has
plane
motion. The
body
is
assumed to be
symmetrical
with
respect
to
its
plane
of motion and hence
may
be considered
to
be
concentrated
in
the
plane
of motion
(see
footnote under Art.
144).
Let the
angular
velocity
and
angular
acceleration of
the
body,
at
the
given
instant,
be
co
and
a,
respectively
(co
and
a
are
the
same
with
respect
to all axes
perpendicular
to
the
plane
of motion and
all
particles
have the
same
co
and
a
at a
given instant,
Art.
134).
Let the motion be
resolved
into a
rotation about an
axis
through
any point
0,
giving
to
the
body,
of
course,
its actual
angular
velocity
and
acceleration,
and a
translation
which
gives
to
each
particle
a motion the same as
that
of
0. Let
ao
denote the
acceler-
ation of the
point
0.
Then,
the acceleration
of
any
particle
at
a distance
r
from
(Fig.
358)
has three
components;
rco
2
, ra,
and
ao,
the
directions of
which are shown for several
particles
in
the
figure.
After
the
components
of
the acceleration
of
any particle
of
the
body
have
been
found,
the
components
of the
resultant
force
(effect-
ive
force)
required
to
produce
the
component
accelerations
may
be
found from
Newton's second
law.
Thus,
as
shown
in
Fig.
359,
the
components
of the effective
force for
any particle
of mass m
are
mat
=
rnra
in
the
direction of a
t
,
ma
n
=
mru
2
in
the
direction of
a
n
,
and
moo
in the direction of
OQ.
For
convenience,
moo
will
be
resolved into
its x- and
^-components,
m(ao)
x
and
m(ao)y ,
as shown
in
Fig.
359.

338
FORCE,
MASS,
AND
ACCELERATION
Resultant
of
Effective
Forces.
The
resultant of
the
effective
forces
for the whole
body
may
now
be
found. The effective
forces
form a
non-concurrent
system
in
the
plane
of motion.
The result-
ant
of such a
system
of forces is
either a
force
or a
couple (Art.
28).
It
will
be
shown,
however,
that
when the resultant
is a
force
it
may
be
resolved,
for
convenience,
into another
force
which acts
through
the
mass-center
of the
body
and a
couple.
The
resultant
of a
non-concurrent force
system
in
a
plane may
be
determined
completely
from the
algebraic
sums
of
the ^-com-
ponents
of
the
forces,
of
the
y-components
of the
forces,
and of
the
moments of
the forces
about an axis
in
the
body through
(Art.
30). Thus,
referring
to
Fig.
359,
and
considering
the
effective forces
for the whole
body
we
may
write:
The
algebraic
sum
of the
^-components
of
the
effective
forces
=
Zm(ao)z-|-2mra:
sin 6
2ma?
2
r
cos
6
The
algebraic
"sum of the
^-components
of the
effective forces
=
Sm(oo)j/
2mm
cos
6
Smco
2
r
sin 6
=
M
(OQ)
y
Mx
a
Myu
2
.
The
algebraic
sum
of
the
moments of
the
effective forces
about
But the
algebraic
sum
of the
^-components
of
the effective forces
is
equal
to the
re-component
of
the
resultant of
the effective
forces,
and
similarly
for the
^/-components. Further,
the
algebraic
sum of
the
moments of the
effective forces
with
respect
to is
equal
to
the
moment
of the resultant
of
the effective forces
with
respect
to 0.
Hence,
summarizing,
The
^-component
of the resultant of the
effective forces
=
M
(OQ)
x
-f
Mya
MX
co
2
.

KINETICS
OF
PLANE
MOTION OF
RIGID BODY
339
The
^/-component
of the resultant
of the
effective forces
=
M(ao)v
-Mxa-Myw
2
.
The
moment
of
the resultant
of
the effective forces about
=
/oa
+
M
y
(oo)
*
MX
(do)
v
.
Relation
between
External and
Effective
Forces.
Since the
effect-
ive
force
for
a
particle
of a
body
is
the
resultant of all
the
forces
acting
on
the
particle,
it is
the resultant
of both
the internal
and
the
external
forces which
act on
the
particle.
Therefore,
the
component,
in
any direction,
of the resultant of
the
effective
forces
for the whole
body
is the
algebraic
sum of
the
components,
in
the
given
direction,
of
all the
internal
forces and all the
external
forces
which act
on the
particles.
Likewise,
the moment of
the
resultant
of the
effective
forces about
any
axis
perpendicular
to
the
plane
of
motion is the
algebraic
sum
of
the moments of all
the
internal
forces
and
all the external
forces
which act on the
particles.
Hence,
if F
denotes
a force and
T
denotes the
moment
(torque)
of a
force,
the above
expressions
are
connected with
the forces
acting
on the
particles according
to
the
following
equations
:
(2F
X
)
Ertemal+(2^)
Internal
=
M(av)
x
+
Mya-
MX
CO
2
(2F
y
) Extemal+(S/'V)
internal
=
M
(OQ)
y
-
Mxa
-
My
U
2
(ST
)
External+(S7o)
internal
But,
since
the internal
forces occur
in
pairs
of
equal,
opposite,
and
collinear forces
(Newton's
third
law),
the
algebraic
sum
of
their
components
in
any
direction,
and the
algebraic
sum
of
their
moments
about
any
axis
perpendicular
to
the
plane
of
motion,
are zero
(that is,
the resultant of
the
external
forces
alone
and the resultant of
the
effective forces
for
the
body
are
identical)
.
Hence,
in the above
equations,
the
terms
which
involve
the
internal
forces
may
be omitted
and
therefore the
equations
expressing
the
relation between
(1)
the
external forces
acting
on
the
body, (2)
the
kinetic
properties
of the
body,
and
(3)
the
change
in
motion
of
the
body
are
:
2F
X
=
M(ao)
x
+Mya
-
(1)

340
F.ORCE,
MASS,
AND
ACCELERATION
The
equations
of
motion,
however,
may
be written in
a
simpler
form.
As
already noted,
the
center, 0,
about which
the
assumed
rotation
takes
place
and about which the
moments
of the
forces
are
taken
may
be
any point
in
the
plane
of motion
of
the
body.
Thus,
if the mass-center
is selected for the
center
about
which
moments
are
taken,
that
is,
if coincides with
G
(Fig. 359)
then,
in
the
above
equations,
x
and
y
are
zero;
ao
becomes
a;
/o
becomes
7;
and
STo
becomes
S7
7
. Hence the
right-hand
member of
each
of the
above
equations
reduces to one
term.
Thus
the
equations
of
motion
for a
rigid body having plane
motion
may
be
written
:
=
Ma
x
(2)
ILLUSTRATIVE PROBLEMS
386.
A
homogeneous
cylinder
which is 3 ft.
in
diameter and
which
weighs
805
Ib.
rolls
down an
inclined
plane
which makes
an
angle
of
30 with
the
horizontal
(Fig. 360).
The
mass-center of the
cylinder
has
an
initial
velocity
r
=
50
ft.
per
sec. The
plane
is
rough
so
that the
cylinder
rolls
without
slipping.
Find
(1)
the
acceler-
ation of
the
mass-center,
(2)
the
magnitude
of
the
friction
force,
and
(3)
the
velocity,
v,
of
the mass-center
at
the end
of
10
sec.
W-8051b.
Solution. The
cylinder
has
plane
motion
under
the action
FIG. 360.
of
three
forces,
F, N,
and W
,
as shown in
Fig.
360. Let the
x- and
7/-axes
be chosen
as shown
in the
figure.
The
equations
of motion
are,
2Fj/
=
May,
(2)
*T
=
Ta.
.
(3)
From
(1),
O/.
(4)
