Seely F.B. Analytical Mechanics for Engineers
Подождите немного. Документ загружается.


FORCES
IN
THE
GYROSCOPE
381
minus
sign
indicates
that
the
sense
of
the acceleration is
opposite
to
that
of the
velocity
for
the
position
of the
particle
as
shown
in
Fig.
390.
Hence,
for
the
position
of the
particle
shown,
the direc-
tion of
co!2?/
is
upwards.
The effective
force,
corresponding
to this
acceleration,
for
any particle
in the
quadrants
OBC and
OCD,
is an
upward
force
perpendicular
to
the
plane
of the disc.
And,
in
the
quadrants
ODA and
OAB,
it is a downward force. The
resultant
of
the effective
forces
for the four
quadrants,
then, may
be
represented
by
the forces
P
(Fig.
390).
These forces form two
couples
which
have
moments with
respect
to
only
one
of
the
rectangular
axes;
namely,
the z-axis.
Further,
according
to
D'Alembert's
principle,
the effective
forces
require
that
external forces act on
the disc
such that
the resultant
of the external forces is
equivalent
to
that
of the effective
forces.
Hence,
an external
couple
must
act on
the
disc
(or
its
axles)
as
indicated
by
the forces
Q
(Fig.
390).
CHANGES
IN
VELOCITIES
DUE
TO
ROTATION
ABOUT
Y-AXIS
(3). Change
in
cop.
Let the
velocity
cop
be
resolved
into
two
components;
one
parallel
and one
perpendicular,
respectively,
to
the
?/-axis
(Fig.
390).
The
component
parallel
to the
?/-axis
under-
goes
no
changes
due to
the rotation
about the
?/-axis;
but
the
component
cop
sin
6,
which
is
perpendicular
to
the
?/-axis,
changes
in
direction due to the rotation
with
angular
velocity
12
about
the
?/-axis.
And, according
to Theorem
II
of
Art.
118,
the
accelera-
tion
0,2
corresponding
to this
change
in
velocity
is
the
product
of the
magnitude
of
the
velocity
and its
angular
velocity
of
turn-
ing,
that
is,
02
=
cop
sin
0-12
=
col2i/,
and
it
is directed
upwards perpendicular
to
the
plane
of
the
disc.
This
acceleration, therefore,
is
equal
to
a\
(see
above)
and
has
the
same
direction
and
sense
as
that of
a\
for
all
positions
of
the
par-
ticle,
as
will be observed
from
a
study
of
Fig.
390.
Therefore,
external
forces
which act
on
the disc
as
a
consequence
of the
changes
in
cop
sin
6 due to the rotation
of
the
disc
about the
?/-axis
must constitute
a
couple
exactly
the
same
as
that
found under
(2).
(4) Change
in
12p
cos
0.
This
velocity
changes
in
direction,
only,
due to
the
rotation
about
the
2/-axis
with
constant
angular
velocity
12.
The
resulting
acceleration,
12
2
Xp
cos 9
or 12
2
#,
is

382
FORCE,
MASS,
AND
ACCELERATION
directed towards
the
center,
on
the
?/-axis,
about
which the
par-
ticle
is
rotating
at the instant. The
corresponding
effective
forces
for
the
particles
of the whole
disc,
therefore,
form
a
parallel
system
in
the
plane
of
the disc.
But,
since the disc
is
symmetrical
with
respect
to the
2/-axis,
this
effective force
system
is
balanced
and
hence no external forces act
on the disc as a
consequence
of the
changes
caused
in
this
velocity by
the
rotation
about the
i/-axis.
It
will
be
noted,
therefore,
that
if
the
disc
is
rotated about
the
2-axis and at
the
same
time is turned
about the
y-axis,
it
will
rotate
about
the z-axis unless
an
external
couple'acts
on
the disc
to
prevent
the rotation. This external
couple
is
called the
gyroscopic
couple.
A
simple experiment
for
demonstrating
the existence of
the
gyroscopic
couple may
be
made
by
holding
a
bicycle
wheel
(dis-
mounted from the
frame)
with one hand on either
end of the
pro-
jecting
(horizontal)
axle.
If
the wheel is
spinning
in
the vertical
plane
about the axle
which is held
in
the
hands,
any attempt
to
turn the axle
(and hands)
in
the horizontal
plane
will cause the
wheel
(and
hands)
to
turn
about
a horizontal axis
perpendicular
to the
axis
of the
wheel unless the hands exert a
couple
to
prevent
this
rotation.
167. The
Moment of the
Gyroscopic Couple.
In
the
preceding
article
it
was shown that the
only
acceleration of a
particle
of
the
disc which
requires
the
action of
external
forces on
the disc
is
a
=
di
+
a>2
co
and that it is directed
perpendicular
to the
plane
of the
disc;
upwards
in
the two
quadrants
BCD,
and
downwards
in
the
two
quadrants
DAB.
The force
required
to
produce
this
acceleration
(effective force)
of
the
particle
of mass
m
is,
F
=
ma
=
mX
2coOt/,
the
direction
of which
agrees
with
that of a.
The
moment of
this effective force for
the
particle,
about
the
x-axis
is,

MOMENT
OF GYROSCOPIC
COUPLE
383
and the sum of
the moments
of the effective forces
for
all
the
par-
ticles
of the disc
is,
22rao)12i/
2
.
But since
o> and
12
are
constant
this
may
be
written,
Zrra/
2
=
27*0)12,
in
which
I
x
is the moment of
inertia of the
.disc
with
respect
to the
x-axis.
Now
the sum
of the moments of the effective
forces is
equal
to
the
moment
of their
resultant,
but the resultant of the
effective
forces is a
couple,
as shown
in
the
preceding
article.
Further,
this
resultant
couple
is
equal
to the
external or
gyroscopic
couple.
Therefore,
the
moment, C,
of the
gyroscopic couple
is
=
27*0)12.
But,
since the disc is
symmetrical
with
respect
to
the x-
and
y-axes,
I
x
is
equal
to
I
v
.
Hence, by making
use
of the
equation
of Art.
89,
27j
may
be
replaced by
the moment
of
inertia of
the
disc
with
respect
to the axis of
spin
(z-axis). Therefore,
the
moment of
the
gyroscopic couple
is,
in which
7
is the
moment of inertia of
the disc
with
respect
to
the
axis of
spin.
The
following
conclusion then
may
be drawn
:
If
a
body
is
sym-
metrical with
respect
to each
of
two
rectangular
axes
(x
and
y)
and
rotates
or
spins
with
a constant
angular
velocity
o?
about a
third
axis
perpendicular
to each
of
the
two
axes
(the
z-axis or
axis
of
spin),
a
couple
having
a
moment
about
one of
the
two
axes
(the
x-axis)
is
required
to maintain an
angular
velocity,
12,
about
the other
of the two axes
(the
2/-axis);
the
moment
of
the
couple
is
equal
to the
product
of
(1)
the
moment
of
inertia,
7,
of
the
body
with
respect
to the axis of
spin (z-axis),
(2)
the
angular
velocity,
o),
of
spin,
and
(3)
the
angular
velocity, 12,
about
the
?/-axis.
The
angular
velocity
12 which is
maintained
by
the
couple
is
called the
velocity
of precession
and the
corresponding
axis
(y-axis)
is called
the
axis
of precession.
The
axis about
which
the

384
FORCE,
MASS,
AND
ACCELERATION
couple
7col2
tends
to
rotate the disc
(z-axis)
is
called the
torque
axis.
Hence
the disc when
spinning
about the z-axis
with
angular
velocity
co
is
said to
precess
about the
i/-axis
when
acted on
by
a
couple
having
a moment
of Jcoft about the
z-axis.
By
referring
to
Fig.
390,
it will be seen that
the
sense
of
rotation
about
the axis of
precession
(?/-axis)
is in
accordance with the fol-
owing
rule:
The sense
of
precession
is
such
as
to turn the axis of
spin
toward
the
torque
axis,
that
is,
the
axis of
spin
tends to become
coincident
with the
torque
axis.
In
the
interpretation
of this
rule the
torque
axis
must be
regarded
as
that
part
or
end
of the z-axis
which,
considered as a
vector
drawn outward
from the
origin, represents
the moment
or
torque
of
the
couple
7col2,
and the
axis of
spin
must
be
regarded
as
that
part
or end of
the z-axis
which,
considered
as a
vector drawn
outward
from the
origin,
represents
the
angular velocity
co
about
the
z-axis.
Thus,
if a
disc
of
weight
W
(Fig.
391)
is
given
an
angular
velocity
co
about
the z-axis and
then
one end
of
the axis
is
placed
on the
vertical
post
at
A,
the
couple
having
a moment Wl
will
cause the disc
(and
z-axis)
to
ro-
tate with
angular velocity
12
about
the
axis
of the
post
(?/-axis)
such
that
Or,
FIG. 391.
Wl
W
12
A;
2
co
g
fcV
in
which
k is
the radius of
gyration
of
the disc
with
respect
to
the
axis
of
spin
(z-axis).
Further,
if
the sense of a? be as
represented
in
Fig.
391,
the sense
of
precession
about the
?/-axis
will be
clock-
wise
as viewed from the
positive
end of the
i/-axis.
For a further
discussion
of
the
gyroscopic
couple
see
Art.
221.

MOMENT
OF GYROSCOPIC
COUPLE
385
ILLUSTRATIVE PROBLEM
423.
The
flywheel
of
an
engine
on a
ship weighs
6000
Ib.
and has a
radius
of
gyration
of
3.75 ft.
It
is
mounted
on
a horizontal axle
which is
parallel
to
the
longitudinal
axis
of
the
ship,
and has a
speed
of 400
r.p.m.
clockwise when
viewed
from the rear.
Find the
gyroscopic
couple
when
the
ship
is
turning
to the left with
an
angular
velocity
of 0.1
rad.
per
sec. What are the axle
reactions if the distance
between the centers
of
bearings
is
4
ft.?
Solution.
The moment of
inertia
of the
flywheel
about the axis
of
spin is,
And,
400X27T
=
2620
slug-ft.
2
.,
_
,
,
=41.9
rad.
/sec.
Hence the
gyroscopic
couple
is,
/wft
=
2620X41.
9X0.
1
=
10,980
Ib.-ft.
In
accordance
with
the rule stated
in
Art.
167,
the
vector
representing
this
couple
is
perpendicular
to the
axis
of the
ship
and
is
directed towards the
right.
The
forces
constituting
the
gyroscopic
couple
are the axle reactions and hence
the
reaction at the forward
bearing
is downwards
and
that at the rear
bearing
is
upwards.
Since
the distance between centers
of
bearings
is
4
ft. the
magni-
tude of
each of these reactions is
10,980
-5-
4
=
2745
Ib. The effect
of the
gyroscopic
motion, then,
is to increase
the
reaction
at the rear
bearing
and to
decrease it at the
forward
bearing.
The
reaction
at each
bearing
due
to
the
weight
of
the
flywheel
is
3000
Ib. Hence the
resultant reaction
at
the rear
bearing
is
3000+2745
=
5745 Ib.
and that at the forward
bearing
is
3000
-2745=
255 Ib.
PROBLEMS
424. A
disc
4
ft. in diameter
(Fig.
392)
rolls
on a
circular track
having
a
radius
of
10 ft.
The
center of the disc has
a
velocity
of
20 ft.
per
sec. The
FIG.
392.

386
FORCE,
MASS,
AND
ACCELERATION
disc is attached
to the
central
axis OY
by
means of
a
rod
which is
collinear
with the z-axis
about
which the
disc
turns. The
disc has
a
flange
similar to
that on a car
wheel.
If the
weight
of the
disc is 450
Ib.
find
the
tension,
T,
in the rod
and the
pressure, P,
of the
track
against
the
flange
of
the
wheel.
426.
A
circular disc is
mounted on
a
horizontal
axle
which
is free
to
rotate
about a
vertical axis as
shown in
Fig.
391,
the
distance
from
the
center of
the
disc to the
vertical axis
being
2
ft.
The
radius of the
disc is 6 in.
and
its
weight
is 10
Ib. If the
disc rotates
about the
horizontal axle
with
a
speed
of
300
r.p.m.,
with
what
velocity
will it rotate
about the
vertical
axis?
Ans. 12
=
157
r.p.m.
426.
The
propeller
of
an
aeroplane
rotates
clockwise when
viewed
from
the
rear. If
the
aeroplane
turns to
the
right
when
moving
in
a
horizontal
plane,
what will be
the
effect
of
the
gyroscopic
couple?
427. The
flywheel
of
an
automobile
engine
is
mounted
on a
horizontal
axle
parallel
to the
longitudinal
axis of the
automobile.
The
flywheel
rotates
counter-clockwise when
viewed from
the rear.
What will
be
the
effect of
the
gyroscopic
couple
on
(a)
the
axle
reactions of the
flywheel,
(6)
the
pressures
of
the
wheels
on
the
road?
GOVERNORS
168.
The
Action of
Governors.
The
governor
of
a
steam
engine, hydraulic turbine,
gas
engine,
or
other
motor,
automatically
regulates
the
supply
of the
steam,
water,
gas,
or
other
fluid,
so
as to
keep
the
driving
force
exerted
by
the
working
fluid
constantly
adjusted
to the
resistance to be
overcome.
The
governor
partakes
of
the
motion of
the
motor so
that
an
increase
in
the
speed
of
the
motor
due to a
decrease
in
the
load,
causes a
corresponding
increase
in
the
speed
of the
moving
parts
of
the
governor
which,
in
turn,
causes,
by
means
of
a suitable
mechanism,
either a
decrease
in
the
pressure
of
the fluid or
a
decrease
in
the
quantity
of
fluid
deliv-
ered to
the
motor.
The
forces
which cause
the
adjustment
of the
controlling
valve
and
which are
brought
into
play by
the
change
of
motion of
the
governor
parts,
depend
in
the main
upon
(1)
the
actual
change
in
the
speed
of
the
moving
parts
or
(2)
the rate
of
change
of
the
speed
of
the
moving parts.
Governors
in
which the
governing
action
depends
mainly
upon
the actual
change
of
speed
of the
gov-
ernor
parts
are
called
centrifugal governors
and
may
be either
pen-
dulum
or
shaft
governors.
Governors
in
which
the
governing
action
depends
mainly
upon
the rate
of
change
of
speed
of
the
moving
parts
are
called inertia
governors
and are
shaft
governors.

THE CONICAL
PENDULUM
387
A
brief
analysis
of the
forces
brought
into
play by
a
change
in
the
motion of
each
of
these
types
of
governors
will here be made.
169. The Conical
Pendulum.
In
Fig.
393
(a)
a
ball of mass
M
and
weight
W
is held
at
the
end of an
arm
AB and
the ball and arm are
caused
to rotate about
an
axle
AO
with
velocity
co. The acceleration
of the
center of the
ball is
directed
towards, 0,
the
center of its
circular
path
and
its
magnitude
is rco
2
.
Hence,
the
force,
R,
required
to
produce
this
acceleration of the
ball
is,
W
R
=
Mru
2
=
rco
2
.
Now,
the
accelerating
(effective)
force R must
be the
resultant of
the external
forces which act on
the
ball. These
external
forces are
the
weight, W,
and the
tension,
T
7
,
in the
arm,
as
shown
in
Fig.
393(6).
If
a
force which
is
equal
but
opposed
to
R
(the
inertia
force)
is assumed to act with W
and
T
as shown
in
Fig.
393(6),
the
three
forces
will be in
equilibrium
and hence
the sum of
their
moments with
respect
to the
point
A is
equal
to zero.
Thus,
(b)
FIG.
393.
W
Therefore,
TFr=
9
in which
co
is
expressed
in
radians
per
second and
g
is
equal
to 32.2
ft.
per
sec.
2
If
the number
of
revolutions
per
minute
(r.p.m.)
is
denoted
by
n,
then
w=
-^7r-
Therefore, h,
may
be
expressed
(in
inches)
by
the
equation,
h
=
35200
(1)
This
equation
shows that the
height
h
of the
cone
depends
only
on
the
speed
of
rotation and
not
upon
the
weight
of the
ball
nor
the
length
of the
arm
AB.
Now,
in
the
pendulum
governor,
the
governing
action
depends upon
the
manner in
which
h
varies
with
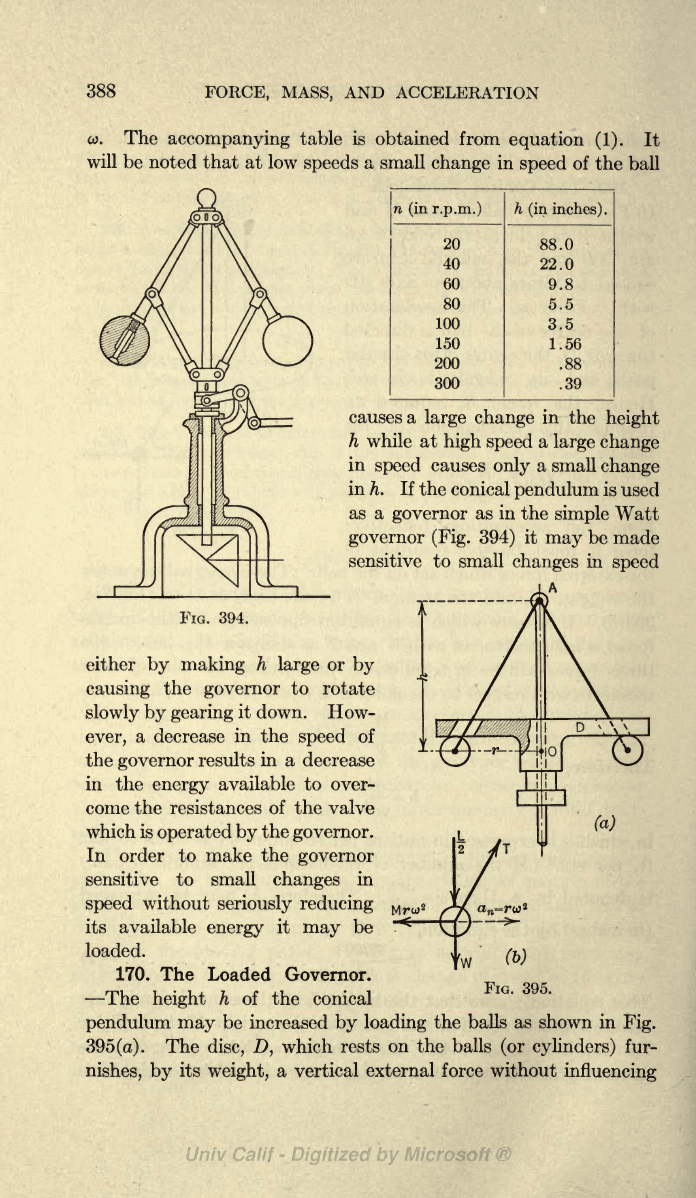
388
FORCE,
MASS,
AND
ACCELERATION
w.
The
accompanying
table
is
obtained from
equation (1).
It
will
be
noted
that
at low
speeds
a
small
change
in
speed
of the
ball
n
(in r.p.m.)

THE PORTER
GOVERNOR
380
the
inertia force of the ball or
cylinder.
If
L
denotes the
weight
of
the disc
(load)
then
-~
is the load
on
each
ball
and the external
Z
forces
W,
o",
and
T
which act
on the ball
form,
with the reversed
effective
(inertia)
force Tlfrco
2
,
a
system
in
equilibrium
as shown
in
Fig.
395(6).
The
sum
of
their
moments,
therefore,
about the
point
A is
equal
to zero.
Thus,
and
by expressing
co
in
revolutions
per minute,
h
is
expressed
in
inches
by
the
equation,
TF+-
^2
35200
W
n
2
This
equation
shows that
the
addition of
the load to the balls of
L
the conical
pendulum
increases the
height
h in
the
ratio
of
l+o^
to
1. For
example,
if
W
=
5 Ib.
and
L
=
30 Ib.
then,
.JL
=1+
J__
4
""'
^2X5
Thus,
the
height
h
of the
simple
conical
pendulum
corresponding
to
a
speed
of
200
r.p.m.
is
0.88
in.
and when loaded
its
height
becomes
4X0.88
=
3.52
in.
For
high
rotative
speeds,
loading
must be
resorted to in
order
to
increase
the
change
of
height
for
a
given
change
in
speed,
that
is,
in order
to
increase the
sensitiveness
of
the
governor.
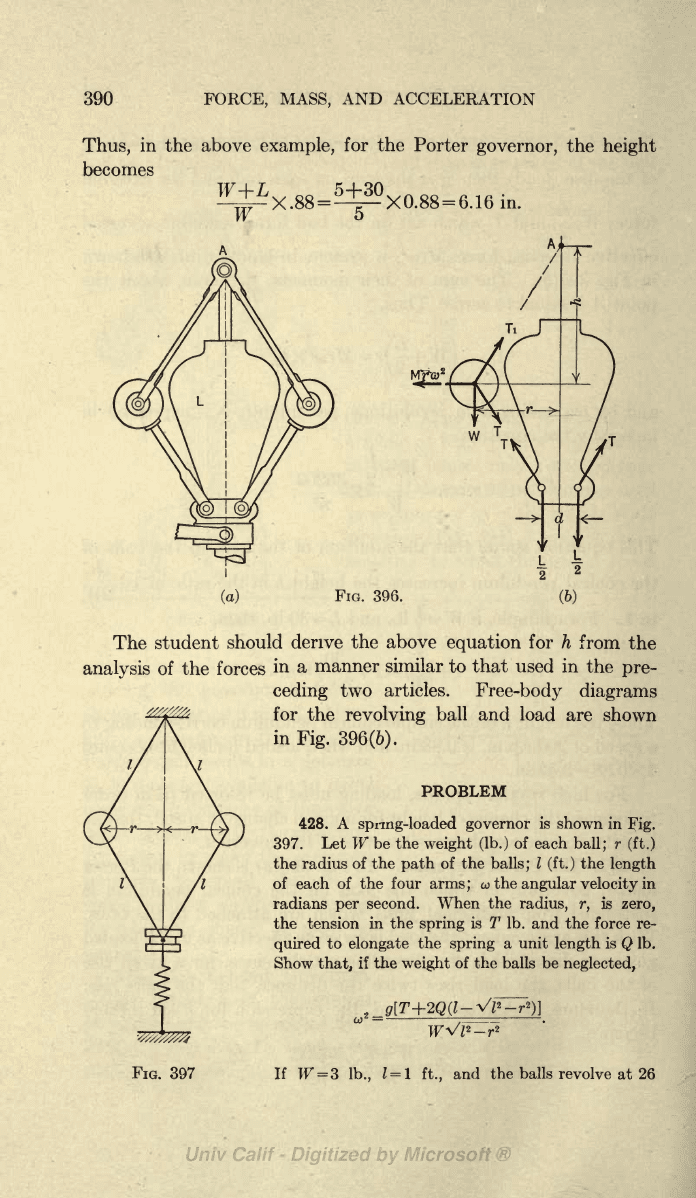
171.
The Porter Governor.
In
Fig. 396(a)
is
shown
the Porter
loaded
governor,
in
which the
load on
the
conical
pendulum
is
suspended
from additional links
which are
attached to
the
balls.
With
this
arrangement
the load is
twice as
effective
as in
the loaded
governor
discussed
in
the
preceding
article,
since,
for
a
given
rise
of
the
balls,
the
load
rises
twice
the
distance
that
the balls
rise.
If,
therefore,
L denotes
the
load,
the
expression
for
h
(in
inches)
becomes,
.TT+L
35200
W
X
n
2
'
390
FORCE,
MASS,
AND
ACCELERATION
Thus,
in the above
example,
for the
Porter
governor,
the
height
becomes
NTfc;
FIG.
396.
The
student
should
derive the
above
equation
for h
from
the
analysis
of the
forces
in
a
manner similar
to that
used
in
the
pre-
ceding
two
articles.
Free-body
diagrams
for
the
revolving
ball
and
load
are
shown
in
Fig. 396(6).
J
PROBLEM
428.
A
spring-loaded governor
is
shown in
Fig.
397.
Let W be the
weight
(Ib.)
of
each
ball;
r
(ft.)
the radius
of the
path
of the
balls;
I
(ft.)
the
length
of
each
of
the four
arms;
o>
the
angular
velocity
in
radians
per
second. When
the
radius, r,
is
zero,
the tension
in the
spring
is
T
Ib. and the force re-
quired
to
elongate
the
spring
a unit
length
is
Q
Ib.
Show
that,
if
the
weight
of the balls be
neglected,
If W
=
3
Ib.,
/
=
!
ft.,
and
the balls
revolve
at 26
