Seely F.B. Analytical Mechanics for Engineers
Подождите немного. Документ загружается.


THE CENTRIFUGAL
SHAFT
GOVERNOR 391
FIG. 398.
rad.
per
sec.
when
r
=
3
in.,
find the tension
in the
spring, assuming
the
modulus
of the
spring
to be
58
Ib.
per
in.
Ans.
T
=
16.8 Ib.
172.
The
Centrifugal
Shaft
Governor.
In the
pendulum gov-
ernors
considered
above,
the
governing
action
is
dependent upon
the
centrifugal
force
(inertia
force)
of
a
rotating
mass
and the
same
is true
for some
types
of shaft
governors.
Thus,
let a
body
of mass
M
be
pivoted
to the
arm of a
flywheel
as shown
in
Fig.
398.
Let the distance
of
the center
of the
mass,
G,
from
the shaft
center,
S,
be
denoted
by
R and
let the wheel rotate
with
an
angular
velocity
co.
The
centrifugal
or inertia
force,
then,
of the mass
M
is
Mru
2
.
As
long
as
co
remains
constant
this
force has a definite
value.
To
hold it
in
equilibrium
a
spring
is
employed.
The moment
of
the
spring
tension about the
point
must therefore
be
equal
to
the
moment of
Mrco
2
about the
same
point
(the
weight
of the
body
is
small in
comparison
with
Mrco
2
and hence
its moment is
neglected)
.
If
now the
angular velocity
of
the wheel increases to
co'
due
to a
decrease
in
the load
on the
engine, assuming
the
value of
r to
remain
constant,
the
centrifugal
force increases to
Afro/
2
and the
excess
force
Mr
(a/
2
co
2
)
causes
the
mass to move outwards
whicji.
in
turn
changes
the
time
of
cut off of the valve
and
adjusts
the
amount of the
working
fluid deliv-
ered
to
the
engine.
PROBLEMS
429.
What
must
be
the initial tension
in the
spring
and the
modulus
of the
spring
so
that the
weight, A,
in
the
gover-
nor
shown in
Fig.
399
will
not
leave
the
inner
stop
and
pass
to the outer
stop
until
a
speed
of 210
r.p.m.
is reached?
Assume
that the
weight
of
A
is 16.1
Ib.,
a
=
3
in.,
6
=
24
in.,
c
=
8
in.,
and
d
=
16
in.
If
the
spring
should
be
placed
farther
from
E
than
16
in.,
would
A
reach
the
outer
FIG.
399.

392
FORCE, MASS,
AND ACCELERATION
stop
with the
wheel
revolving
at the same
speed
that it had
when
A
left
the
inner
stop?
Ans.
7
1
=
2421b.;
modulus
=
45.4 Ib.
per
in.
430. Given the
arrangement
as shown in the
previous
problem,
with the fol-
lowing
data
:
a
=
3
in.,
b
=
20
in.,
c
=
9
in.,
d
=
12
in.,
modulus of
spring
=
50
in.
If
the mean
speed,
n
,
is
200
r.p.m.,
what
must
be the
weight
of A
for a
coefficient
of
steadiness, ,
of
0.01,
where
HI
and n
2
denote the maximum
wo
and
minimum
speeds respectively?
Ans. W
=
14.85 Ib.
173.
The Inertia Shaft
Governor. As
already noted, governors
in which
the
regulating
action
depends upon
a
change
in
the cen-
trifugal
force,
whether
of
the
pendulum
or of the shaft
type,
are
called
centrifugal governors.
It
is
important
to note that with
centrifugal governors
there
must
be an actual
change
of
speed
to
give
a
governing
action.
In
the
inertia
governor,
however,
the
governing
action is
entirely
differ-
ent.
Thus,
in
Fig.
400,
let a
mass
M
be
pivoted
to the
arm
of a
flywheel
so that the
pin,
0,
passes
through
the center of
mass.
FIG. 400.
The
centrifugal
force of the mass
is balanced
by
the
pin
reaction
at
and hence the
centrifugal
force is not
involved in
the
governing
action.
In
order to show how the forces which
cause the
governing
action
arise,
let
it
be
assumed first that the wheel of
Fig.
400 is
standing
still and that the
mass is turned on the
pin,
0,
with
an
angular
acceleration
a. To
produce
this
acceleration a
moment, T,
is
required
having
a
magnitude,
in which
/o
is
the
moment of
inertia
of the mass with
respect
to
the
pin
0.
Now,
if
a
change
in
speed
of
the wheel
(and shaft)
occurs,
due to
a
change
in the
load on the
motor,
each
particle
in
the
mass
M,
by
virtue of its
inertia,
will tend to
maintain
its
linear
velocity
and hence will turn relative
to the
wheel
about
the
axis
and
thereby
cause the valve mechanism
to exert
forces
on the
mass,

COMPARISON
OF
TWO TYPES
OF
GOVERNORS
393
the
moment
of which
about
will be
equal
to
/oa.
In
this
type
of
governor,
therefore,
the
governing
action
depends
not
upon
the
actual
change
of
speed
but
upon
the
rate of
change
of
angular
speed,
that
is, upon
the
angular
acceleration of
the wheel
or
engine
shaft.
Shaft
governors
of
this
type
are called
inertia
governors.
174.
Comparison
of
the Two
Types
of Governors.
Centrifugal
and
inertia
governors
differ
in
two
important particulars.
Since,
in
the
centrifugal
type,
the
governing
force
depends
upon
the
change
in the
speed
there
must
be an increase
(or
decrease)
in
the
speed
of
a definite
amount before
the
governing
force is
sufficient
to
move
the
valve
gear
against
the frictional forces.
In
the
inertia
governor,
on
the
other
hand,
the
governing
force is
proportional
to
the
angular
acceleration
and,
in
general,
the
angular
acceleration
of
the
governing
mass is
greatest just
at
the
beginning
of
the
change
of
speed;
hence,
before
the
speed
of
the shaft
has
changed appre-
ciably,
the
governor
begins
to act
although
the
change
in
the
centrifugal
force is small. It
follows
then
that the
inertia
gov-
ernor acts
more
quickly
and
holds
the
speed
within
much
smaller
limits than does
the
centrifugal governor.
The
centrifugal type
of
governor,
however,
has
one
essential
property
not
possessed
by
the inertia
type.
The
centrifugal
force
Afrco
2
varies
somewhat
for
different
positions
of the
balls
in
Figs.
393,
394, 395,
or
396,
and of the
body
in
Fig. 398,
but for
any
fixed
position
it
must have a fixed definite value
which is deter-
mined
by
the
weight
of the
balls
(and
load on
the
balls)
in
the
pen-
dulum
governors
and
by
the
spring
tension
in
the
shaft
governor.
It
follows
that,
with the
governor
in
a definite
position,
the
speed,
co,
of the shaft
has a definite
value and
therefore
the
speed
of the
engine
is
fixed.
Thus,
if
it
is
determined that
the
speed
shall be
200
r.p.m.
and
the
governor
is
properly
adjusted,
the
speed
cannot
vary
much
from that
speed
as
long
as
the
governor
is
operative.
The
speed
may
sink
to 195
r.p.m.
under a
heavy
load or rise to
205
r.p.m.
with
a
light load;
but the
centrifugal
force
imposes
the
average
speed
of 200
r.p.m.,
and
the
engine
cannot be made to
run at
a different
average speed
without
some
adjustment
of
the
governor,
such
as the
addition
of a
weight
or
an
increase
in
the
spring
tension.
175.
Analysis
of
Forces in
the
Rite's
Inertia Governor.-
In
the shaft
governor
known
as
the
Rite's
inertia
governor,
a
combination
of
the
two
governing
actions
discussed
above
is
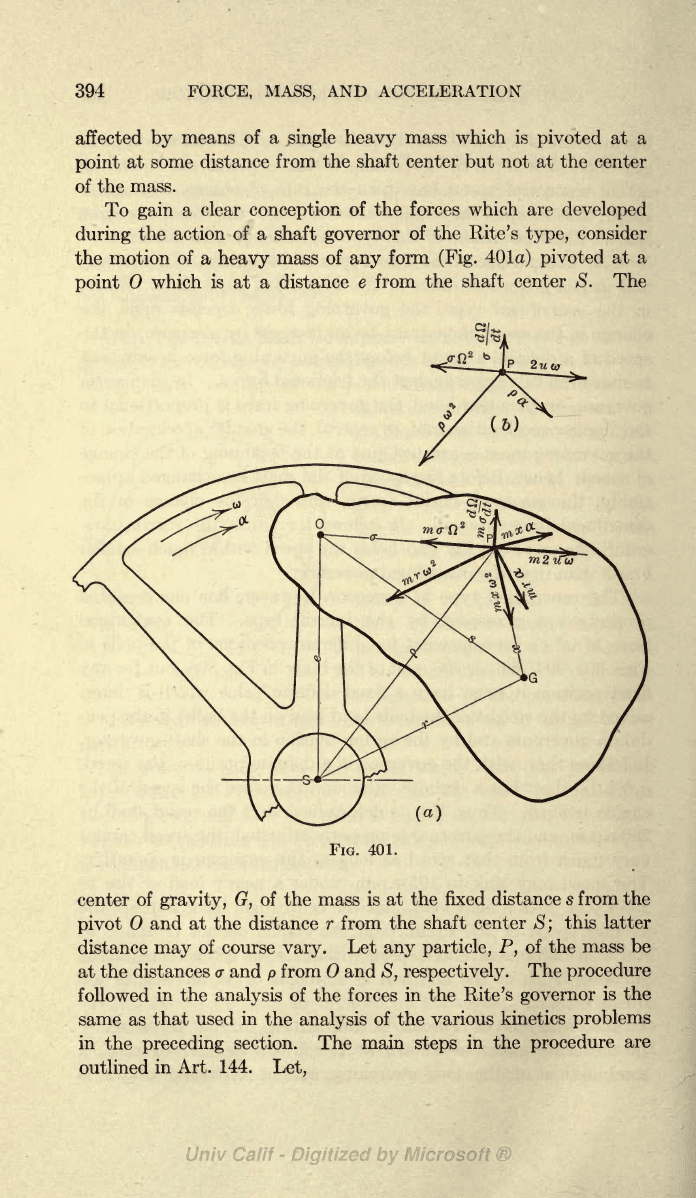
394
FORCE,
MASS,
AND
ACCELERATION
affected
by
means of a
single
heavy
mass which is
pivoted
at a
point
at some
distance
from the shaft center but not
at
the center
of the
mass.
To
gain
a
clear
conception
of
the forces which are
developed
during
the action of a
shaft
governor
of
the
Rite's
type,
consider
the
motion
of
a
heavy
mass of
any
form
(Fig.
40
la)
pivoted
at
a
point
which is at a distance
e
from
the
shaft center S. The
FIG.
401.
center
of
gravity,
G,
of the mass
is at the
fixed
distance s from
the
pivot
and at the distance
r from the
shaft
center
S',
this
latter
distance
may
of course
vary.
Let
any particle,
P,
of the
mass
be
at the
distances o- and
p
from and
S, respectively.
The
procedure
followed
in
the
analysis
of the forces
in the
Rite's
governor
is the
same
as that
used
in
the
analysis
of
the
various
kinetics
problems
in
the
preceding
section. The main
steps
in
the
procedure
are
outlined
in Art.
144.
Let,

FORCES IN RITE'S INERTIA GOVERNOR
395
W
M
=
=the
mass
of
the
body
which
is
pivoted
at
0;
\J
o>
=
the
angular
velocity
of
the
wheel about the
shaft
center S
;
12
=
the
angular
velocity
of the mass
M
about
the
pivot
0;
u
=
<rSl
=
the linear
velocity
of
P
relative
to
;
a
=
-y
=the
angular
acceleration
of
the
wheel;
a/
=
~T
f
=
the
angular
acceleration
of
the mass
M
about
;
lo
=
the
moment
of
inertia
of
the
mass
M
with
respect
to
the
pivot
0,
and
7=the moment
of inertia of the mass
M
with
respect
to
the
center
of
gravity
G.
Acceleration
of Any
Particle P.
According
to
CoriohV law
(Art.
130),
the acceleration
of
the
particle
P
(Fig.
4016)
has
three
components
as follows:
(1)
The acceleration
that
P
would
have
considering
the
wheel
to
be
stationary
and the
mass to
be
rotating
about
0;
this
accelera-
tion
may
itself be
resolved
into,
A radial
component
o-fl
2
along
PO,
and a
tangential
component
cr
=
<jd
f
perpendicular
to
PO;
(2)
The acceleration
of that
point
of
the
wheel which
is
coin-
cident with
P;
this
component
may
likewise be
resolved
into,
A radial
component
pco
2
along PS,
and a
tangential
component
=
pa.
perpendicular
to PS.
dt
(3)
The acceleration
2uu
along
OP.
These
components
of the acceleration
of the
point
P
are
shown
in
Fig.
401(6).
No
attempt
has been
made
to
show the
magnitudes
of the
accelerations
by
the
lengths
of
4ihe
vectors.
It
will
be found convenient to
replace
the
components
pw
2
and
pa
by
four other
components, parallel
and
perpendicular,
respect-
ively,
to
the
lines SG
and
PG.
These four
components
may
be
obtained
by
direct resolution
or
by
considering
the motion
of
the
wheel
to
be
replaced
by
a rotation
and a
translation
(Art.
134).
Thus,
at
any
instant,
the rotation
of
the
wheel
about
its
shaft, S,
with
angular
velocity
co
and
angular
acceleration
a
may
be con-
sidered as a
rotation
with
the
same
angular
velocity
and acceleration

396
FORCE,
MASS,
AND
ACCELERATION
about a
parallel
axis in
the wheel
which
passes
through
the
point
G,
and a translation of the
wheel
in
a
direction
perpendicular
to
SG.
The
components
pco
2
and
pa
which,
as
found
above,
were
due
to the rotation
of
the
wheel about its
shaft S
will
now
be
replaced
by (1)
the acceleration
of
the
point
P
due to
the rotation
of
the
wheel about G and
(2)
the acceleration
due to the
translation,
which
is common to all
points
of
the
wheel. The
accelerations
of
the
point
P
of the
wheel
(that is,
the
point
on
the wheel
which
is
coincident with the
point
P
of the
mass
M),
then, are,
xco
2
along
PG
and
xr-
=
xa
perpendicular
to
P(7,
which are
due to the
rotation of
the
wheel about
G; and,
ror
parallel
to
SG,
and
ra.
perpendicular
to
SG,
which are due to
the
(curvilinear)
translation of
the wheel.
Moment
of Effective
Forces
about the Pin
0. The
moment
of
the
effective
forces for
the whole
body
with
respect
to the
pin
will
now be found since the rotation of the mass about the
pin
is the
cause of the
movement
of
the valve mechanism.
And,
the moment
of
the
effective forces must be
found
in order to
determine
the
moment of
the external forces
which
are
brought
into
action
as a
result
of
this rotation
and which are exerted
on the valve mechan-
ism.
For,
by
D'Alembert's
principle,
the
sum of the moments
of
the external forces must
be
equal
to the sum of the
moments
of
the
effective forces.
The
accelerating
or effective
force
for the
particle
P of
mass
m
must
have a
component
in
the direction
of each of the
acceleration
components,
the
magnitude
of each
component
of the force
being
the
product
of
the mass
m
of
the
particle
and the
acceleration
component.
These
seven
components
of the
effective
force
for
the
particle
are
shown
in
Fig.
401,
acting
at
the
particle
P.
The
sum of
the moments of
these
forces,
for
all
the
particles,
about
the
pin
may
be found as
follows :
(1)
The
components
mo-12
2
and
2muco are
collinear
and
act
through
the
pin
0.
The
resultant
of these
components,
therefore,
FORCES
IN RITE'S
INERTIA
GOVERNOR
397
for the whole
body,
is a force which
acts
through
0. The
sum of
the
moments of these
components
about
the
point
0,
then,
is
equal
to zero and
hence,
these
forces
have no influence
in
the
prob-
lem under discussion.
Their
only
effect
is
to
produce
a
pin pres-
sure
at 0.
(2)
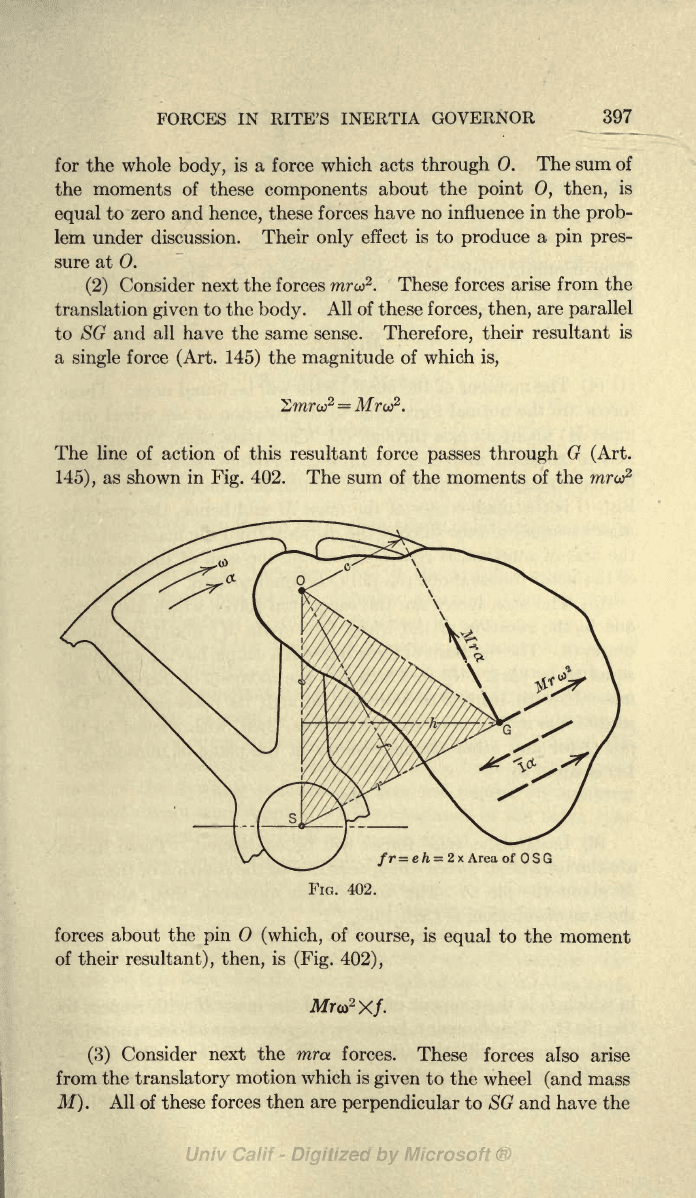
Consider next the forces
wrco
2
.
These
forces arise
from the
translation
given
to
the
body.
All of these
forces,
then,
are
parallel
to
SG
and
all have
the
same sense.
Therefore,
their
resultant
is
a
single
force
(Art. 145)
the
magnitude
of
which
is,
Srarco
2
=
Mrco
2
.
The
line of
action
of
this resultant force
passes through
G
(Art.
145),
as
shown
in
Fig.
402.
The sum of the moments of the
mrco
2
2 x
Area
of
S G
FIG. 402.
forces about
the
pin (which,
of
course,
is
equal
to
the
moment
of their
resultant), then,
is
(Fig. 402),
Mrco
2
X/.
(3)
Consider
next the
mra
forces.
These
forces
also
arise
from
the
translatory
motion which is
given
to
the
wheel
(and
mass
M).
All
of these
forces then are
perpendicular
to
SG and
have the

398
FORCE,
MASS,
AND
ACCELERATION
same sense. Their
resultant,
therefore,
is a
single
force
(Art. 145)
having
a
magnitude
equal
to
'Zmra
=
Mra.
This
resultant force also
passes
through
G.
The sum
of
the
moments
of the mra
forces with
respect
to
the
pin 0, then,
is
(Fig.
402),
MraXc.
(4)
The moment of the mxu>
2
forces will
be
found next.
These
forces are the normal
forces due to
the rotation
of the
wheel
(and
mass
M)
about an axis
through
G.
They
pass,
then,
through
the
a.xis of
rotation and
their
resultant, therefore,
is a
single
force
having
a
magnitude
equal
to
Mx^
2
which acts
through
G
(Art. 22).
But,
G
is the
mass-center of the
mass
M
and
hence,
the
quantity
Mxu
2
is
equal
to zero
since
x,
the distance from
the
mass-center to
the axis of
rotation,
is
zero.
Therefore,
the sum
of
the moments
of
the
mxco
2
forces
about the
pin
is
equal
to zero.
(5)
The
mxa
forces are the
tangential
forces
which
also arise
due
to the rotation of
the wheel
(and
mass
M)
about the mass-
center G. The
resultant of these forces is a
couple
having
a moment
equal
to
la
(Art. 146)
in
which
/
is the moment
of
inertia
of
the
mass
M
with
respect
to the axis
through
its
mass-center.
The
sum of
the moments of the
mxa
forces,
then,
with
respect
to the
pin
(or
any
other moment-center in
the
plane
of
motion,
Art.
15)
is
equal
to
(6)
Lastly,
the mad forces will be
considered. These forces
are the
tangential
forces which
arise
due
to the
rotation of the mass
M
about the
pin
0. The sum of their
moments, then,
about
0,
the axis of
rotation,
is
(Art. 146),
in which
/o
is the
moment of inertia of the mass
M
with
respect
to
the
pin
0. This
moment, however,
for
governors
as
constructed,
is
small
compared
with
the other moments since
a' is small.
There-
fore,
the
moment
/o</
will be
neglected
in the
subsequent
discus-
sion.

FORCES
IN
RITE'S INERTIA GOVERNOR
399
The Moment
of
the External
Forces
and
the
Governing
Action.
As noted
above
the
moments of the external
forces must be
equal
to the
sum of
the
moments of the
effective forces.
Or,
if
the
effective
forces were
reversed,
external forces would have to act
on
the
body
such
that
they
would
hold the reversed effective
(inertia)
forces
in
equilibrium.
Hence,
external forces must
act
on
the mass
M
such
that the
moments
of
the
external forces will
hold
in
equilibrium
the moment
(Fig.
402),
(1)
of the
centrifugal
force,
and the moment
.....
(2)
which
is called
into
action
only
when the
angular acceleration, a,
exists.
It will
be
noted, therefore,
that
if
the
angular velocity, co,
of the
flywheel
(and
engine)
remains
constant,
that
is,
if the
angular
acceleration, a,
of the
flywheel
is
equal
to
zero,
the
moment
(Mehu
2
)
of the
centrifugal
force has a constant
magnitude
and must be
equilibrated
by
the moment of the
spring
tension.
Further,
if GO
is
constant the
only
external moment
acting
on the
mass
M
is
the
moment of the
spring
tension
since
a,
and conse-
quently
Ti,
is
equal
to
zero.
Thus,
the moment
T^
unlike the
moment
T
c
,
is called into
existence
only
when there is
a
change
in
speed
of the
flywheel
and hence
it does
not
require
an
opposing
moment
except
that
supplied by
the resistance of
the
valve
gear
as the
valve
gear adjusts
itself to the
new
speed.
To
explain
further the
governing
action in
the
Rite's
governor,
let
it
be assumed that the motor
is
running
at a
constant mean
speed
wo
;
the
moment
T
c
(
=
Mehu>
2
)
of the
centrifugal
force is then
just
balanced
by
the moment of the
spring
tension
which
may
be
denoted
by
T
s
.
Now,
let the load on
the
motor
be
reduced;
the
excess
of the effort
over the
resistance
will
cause
the
moving
parts
of the motor
(flywheel,
shaft,
etc.)
to
rotate
with an increased
speed,
coi,
and the
moment
T
c
will
increase from
Mehco
2
to
Mehui
2
.
The
difference,
Meh(u\
2
w
2
),
is
the
excess of
the moment
of the
centrifugal
force
over
that of
the
spring
tension
and
is
available
for
producing
a
movement
of
the
governor
parts.
However,
if

400
FORCE, MASS,
AND
ACCELERATION
this difference alone is
depended
on for
moving
the valve
mechan-
ism,
the
speed
coi
must be
considerably
in
excess of the mean
speed
o)o
before the
governor
and
attached
valve
will
move.
On
the
other
hand,
the
very
instant the
change
in
speed
begins,
the
angular
acceleration,
a,
of the
mass
M
comes
into existence
and,
with
it,
the
unbalanced
moment
Tt
which
is available for
moving
the
valve
gear.
In
the
ideal
governor,
therefore,
there is needed
a
moment,
T
C)
of a
centrigufal
force which
is
just
sufficient to
fix
a mean
speed
wo,
and a
moment,
Tt,
of
considerable
magnitude
which
arises from
the
rate of
change
of
the
angular
velocity
of
the
flywheel
and which
provides
for
the
adjustment
of the
governor.
Distribution
and Position
of
the Mass M.
An
inspection
of
equation
(2)
shows
that,
with
a
given
value of
r,
the
magnitude
of
the moment
T
t
depends
on
M
and
7.
With
a
heavy
flywheel,
a
is
likely
to be
small;
hence,
to
make
T*
large,
either
M
must be
made
large
or,
for a
given
M,
I
may
be made
large
by
constructing
the
swinging
mass
M
in
two
parts
which are removed a
considerable
distance
from the center
of
gravity, G,
and
are
joined by
a bar
(see Figs.
404
and
405).
Further,
the
governing
action of the
swinging
mass
will
depend
largely
on the relative
position
of
the
points
0,
S,
and G.
Thus,
in
Fig.
403,
let
a circle be drawn
having
a diameter
equal
to OS
or
e and
let
the sense of
rotation
of the shaft be assumed
clockwise.
As
discussed above
there are three
moments
(Mrac,
la,
and
Meh(ui
2
o)o
2
))
which
are effective
in
producing
the
adjustment
of
the
governor.
Now these
three
moments
may
or
may
not
have
the
same
sense,
depending
on the location
of the
point
G. If
a
counter-clockwise
sense is denoted
by
+
and a
clockwise sense
by
,
the
following
table indicates
the
sense of
each of the
three
moments about
for
a location
of G
in
each of the four
regions,
I,
II, III,
and IV
indicated
in
Fig.
403.
I II III
IV
Mrac
+
+
la
+ + +
+
For
the
most
powerful
governing
action,
the
mass-center,
G,
of
the
mass
M,
therefore,
should
be located
in
region
I.
If
(7
is
