Schulz M. Control Theory in Physics and Other Fields of Science: Concepts, Tools, and Applications

Подождите немного. Документ загружается.

3.1 Introduction to Linear Quadratic Problems 65

∂z

∂Y



∂h

∂Y





∂h

∂Y





AY + ψ

(r)



= AY +

∂h

∂Y

AY + ψ

(r)

∂h

∂Y

(r)

= Az −



Ah −

∂h

∂Y

AY − ψ

(r)



∂h

∂Y

(r)

. (3.11)

We determine the open function h by setting

h = Ah −

∂h

∂Y

AY = ψ

(r)

. (3.12)

This equation has a unique solution if the eigenvalues of the introduced op-

erator

are nonresonant. To understand this statement, we consider that

the matrix A has the set of eigenvalues λ = {λ

,...,λ

} and the normalized

eigenvectors {e

,...,e

}. The vector Y can be expressed in terms of these

bases, Y = η

+ ···+ η

. The eigenvectors of

are the following vector

monomials

m,γ

= η

...η

(3.13)

with m = {m

,...,m

}.Them

are nonnegative integers satisfying m

···+ m

≥ 2. Note that

acts in the space of functions which have an

asymptotic behavior h ∼|Y |

with r ≥ 2for|Y |→0. We remark that

Aϕ

m,γ

= λ

m,γ

and



α,β

∂ϕ

m,γ

∂Y

αβ



∂ϕ

m,γ

∂η

=(m, λ) ϕ

m,γ

, (3.14)

where (m, λ) is the euclidean scalar product between the vectors m and λ.

Thus we ﬁnd

m,γ

=[λ

− (m, λ)] ϕ

m,γ

, (3.15)

i.e. the operator

has the eigenvalues λ

− (m, λ). If all eigenvalues of

have nonzero values, (3.12) has a unique solution. That requires (m, λ) = λ

Otherwise, we have a so-called resonance λ

=(m, λ), and

is not reversible.

Suppose that no resonances exist. Then the solution of (3.12) deﬁnes the

transformation function h(y) such that

˙z = Az +

∂h

∂Y

(r)

(Y ) (3.16)

Comparing the order of the leading terms of h and ψ

(r)

we ﬁnd that the prod-

uct ψ

(r)

(Y ) ∂h/∂Y is of an order r +1 in |Y |. Considering the transformation

between z and Y , we arrive at

˙z = Az + ψ

(r+1)

(z) , (3.17)

where ψ

(r+1)

(z) is a nonlinear contribution with a leading term proportional

to |z|

r+1

. The repeated application of this formalism generates an increasing

order of the leading term.

66 3 Linear Quadratic Problems

In other words, the nonlinear diﬀerential equation approaches step by step

a linear diﬀerential equation. This is the content of the famous theorem of

Poincar´e[2]. In the case of resonant eigenvalues the Poincar´e theorem must

be extended to the theorem of Poincar´e and Dulaque [2]. Here, we get the

following diﬀerential equation instead of (3.17):

˙z = Az + w(z)+ψ

(r+1)

(z) , (3.18)

where w(z) contains the resonant monomials. The convergence of this pro-

cedure depends on the structure of the eigen value spectra of the matrix A.

If the convex cover of all eigenvalues λ

,...,λ

in the complex plane does

not contain the origin, the vector λ = {λ

,...,λ

} is an element of the so-

called Poincar´e region of the corresponding 2N-dimensional complex space.

Otherwise, the vector is an element of the Siegel region [3].

If λ is an element of the Poincar´e region, the above-discussed procedure

is convergent and the diﬀerential equation (3.10)or(3.7) can be mapped for-

mally onto a linear diﬀerential equation for nonresonant eigenvalues or onto

the canonical form (3.18). In the ﬁrst case, the stability of the original dif-

ferential equation (3.7) is equivalent to the stability of the linear diﬀerential

equation ˙z = Az. That means especially that, because of (3.7), the linearized

version of the original diﬀerential equation system is suﬃcient for the deter-

mination of the stability of the ﬁxed point Y = 0. In the second case, we have

to analyze the nonlinear normal form (3.18) for a study of the dynamics of

the original system in the neighborhood of the ﬁxed point Y =0.Ifλ is an

element of the Siegel region, the convergence cannot be guaranteed.

The Poincar´e theorem allows a powerful analysis of the stability of systems

of diﬀerential equations which goes beyond the standard method of linear ap-

proximation. In particular, this theorem can be a helpful tool classifying the

above-discussed self-stabilization of a system and many other related prob-

lems.

In the case of a one-dimensional system only one eigen value λ = A exists.

Then the ﬁxed point Y = 0 corresponds to a stable state for λ<0 and to an

unstable state for λ>0. Special investigations considering the leading term

of the nonlinear part of (3.10) are necessary for λ =0.

Another situation occurs for a two-dimensional system. Here we have two

eigenvalues, λ

and λ

. If resonances are excluded, the largest real part of the

eigenvalues determines the stability or instability of the system. A resonance

exists if λ

= m

+ m

or λ

= m

+ m

where m

and m

are

nonnegative integers. In this case we expect a nonlinear normal form (3.18)

containing the resonant monomials.

Let us illustrate the formalism by using a very simple example. The eigen-

values λ

= −λ

=iΩ, obtained from the linear stability analysis, are usually

identiﬁed with a periodic motion of the frequency Ω. But this case contains

two resonances, namely, λ

=2λ

+λ

and λ

= λ

+2λ

. Thus the stationarity

of the evolution of the corresponding nonlinear system of diﬀerential equations

3.1 Introduction to Linear Quadratic Problems 67

Fig. 3.2. Stable ﬁxed point for Im c<0, limit circle for Im c = 0 and unstable

behaviour for Im c>0

(3.10) is no longer determined by the simple linear system

˙η

=iΩη

and

˙η

= −iΩη

, but by the normal system

˙η

=iΩη

+ c

and ˙η

= −iΩη

− c

. (3.19)

The substitutions x

= η

+iη

and x

=i(η

− iη

) and the agreement

= x

+ x

lead to the real normal form

˙x

= Ωx

Im c − x

Re c] (3.20)

and

˙x

= −Ωx

Re c + x

Im c] , (3.21)

where the real structure of the diﬀerential equations requires c

= c and

= c. Such a structure is already expected after the ﬁrst step of the Poincar´e

algorithm applied onto (3.10). Only the two parameters Re c and Im c are still

open. All other nonlinear terms disappear step by step during the repeated

application of the reduction formalism. However, it is not necessary to exe-

cute these steps because the resonance terms remain unchanged after their

appearance. The stability behavior follows directly from the dynamics of x

We obtain from (3.21)

∂x

∂t

Im c

. (3.22)

Thus, the system is stable for Im c<0 and unstable for Im c>0, see Fig. 3.2.

Obviously, we need only an estimation about the sign of the quantity Im c,

which is usually obtainable after a few iterations of the above-introduced

Poincar´e algorithm.

The linear system is written in the standard form considering the representation

in terms of the eigen vectors of the matrix A.

68 3 Linear Quadratic Problems

Ljapunov Theorems

Now we come back to the more general non-autonomous diﬀerential equation

(3.6). Let us assume that we may construct a scalar function V (Y, t) with

V (0,t) = 0 which is positive deﬁnite and whose total derivative along the

solutions of (3.6) is not positive. A function with these properties is called a

Ljapunov function, which means if Y (t, Y

) is the solution of (3.6) with the

initial condition Y (t

)=Y

we expect from our construction

V (Y (t, Y

),t)=

∂V

∂Y



Y =Y (t,Y

)

H(Y (t, Y

),t)

∂V

∂t



Y =Y (t,Y

)

≤ 0 . (3.23)

Because V (Y,t) > 0 and the fact that the derivatives along each solution of

(3.6) are negative, we get immediately the result

V (Y (t, Y

),t) ≤ V (Y

,t) . (3.24)

Since the Ljapunov function V (Y, t) is positive deﬁnite, we always ﬁnd a

strictly monotone increasing continuous function Ψ

−

with Ψ

−

(0) = 0 which

satisﬁes

V (Y,t) ≥ Ψ

−

(Y ) (3.25)

for all Y and t. The function Ψ

−

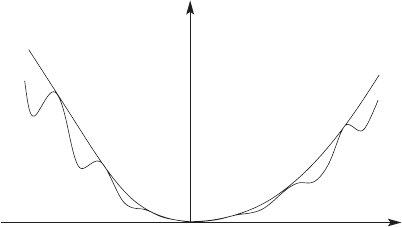
is also called a conical function (Fig. 3.3).

Then, we can always determine an >0sothat

V (Y

,t) <Ψ

−

() (3.26)

for all Y

 <δ. We take δ



= min(δ, ). Then the relation Y

 <δ



implies

Y

 < as well as V (Y

,t) <Ψ

−

() . (3.27)

In principle, we may ﬁnd for each δ



a corresponding  so that the relation

(3.27) is satisﬁed for all Y

 <δ



. Let us now ask, if a solution with the

initial condition Y

 <δ



can become

V(Y,t)

−

Fig. 3.3. A positive deﬁnite function V and the corresponding conical function Ψ

−

3.1 Introduction to Linear Quadratic Problems 69

Y (t, Y

) >, (3.28)

for all t above a critical time t

if the total derivative of V (Y,t) along

the solution Y (t, Y

) is not positive. If this were the case, we would expect

Y (t

) =  (3.29)

due to the continuity of the solution Y (t, Y

). But this is because of the

conical bound property (3.25),

V (Y (t

),t

) ≥ Ψ

−

(Y (t

))=Ψ

−

() , (3.30)

in contradiction to (3.27). Thus we conclude that the existence of a positive

deﬁnite function V (Y,t) with V (0,t) = 0 and whose total derivative along

the solutions of (3.6) is not positive is a suﬃcient condition for the stability,

namely that each solution of (3.6) with suﬃciently small initial conditions

Y

 <δ



is always localized in the phase space onto the region Y (t, Y

) <

. This is the content of Ljapunov’s ﬁrst stability theorem. But this theorem

gives no information about the convergence behavior of Y (t, Y

)fort →∞.

For this problem we need an additional requirement, namely the decrescent

property of V (Y,t). The function V (Y, t) is called a decrescent if there exists

another conical function Ψ

so that for all Y and t

V (Y,t) ≤ Ψ

(Y ) (3.31)

holds (Fig. 3.4). Since V (Y, t) ≥ 0 and the derivatives along the solutions of

(3.6) are negative, we expect

lim

t→∞

V (Y (t, Y

),t)=V

∞

≥ 0 . (3.32)

The claim is now to show that V

∞

= 0 for each decrescent Ljapunov function.

Obviously, the functions Ψ

−

and Ψ

cover V (Y, t). Furthermore, since the

total derivative dV/dt along the solution is negative deﬁnite, we always ﬁnd

a conical function Φ such that

V(Y,t)

Fig. 3.4. A positive deﬁnite decrescent function V bounded by the conical function

70 3 Linear Quadratic Problems

V (Y (t, Y

),t) ≤−Φ (Y (t, Y

)) . (3.33)

Hence, if V

∞

> 0, we conclude that for all t the inequality V (Y (t, Y

),t) ≥

∞

and therefore Ψ

(Y (t, Y

)) ≥ V

∞

hold. The last inequality requires

that there exists a ﬁnite ε such that

Y (t, Y

)≥ε (3.34)

for all t. But then we have because of (3.33) the inequality

V (Y (t, Y

),t) ≤−Φ (ε) (3.35)

and therefore





V (Y (t



),t



)=V (Y (t, Y

),t) − V (Y

)

≤−Φ (ε)(t − t

) (3.36)

i.e., we get for t →∞ always V

∞

< 0ifΦ (ε) = 0 in contradiction to (3.32).

The only possible way to avoid contradictions is that Φ (ε) = 0. Because

of the conical character of Φ, we then have ε = 0 and therefore, because of

the required decrescent character of the Ljapunov function, V

∞

= 0. Hence,

we obtain the second Ljapunov theorem: the successful construction of one

decrescent Ljapunov function is suﬃcient for the convergence

lim

t→∞

Y (t, Y

) = 0 (3.37)

and consequently for the stability of the ﬁxed point Y =0.

We illustrate this behavior with the simple example of a particle in the

potential v(x) ≥ 0 under a Newtonian friction with the coeﬃcient γ. The po-

tential may monotonously increase if |x| increases. Let Y be a two component

vector (x, p). Then the evolution equations read

˙x = p/m and ˙p = −v



(x) − γp . (3.38)

A possible decrescent Ljapunov function is then

V (x, p, t)=

+ v(x) (3.39)

because its derivatives along the trajectories are given by

p ˙p

+ v



(x)˙x = −

≤ 0 . (3.40)

Thus we get the well-known result that the ﬁxed point Y = 0 is stable.

If we come back to our original control problem, we may summarize that

the stability analysis is a ﬁrst step to decide if a certain system requires a

control in order to stabilize the optimum trajectory against possible pertur-

bations. If the system is unstable, such a control is absolutely necessary. On

the other hand, a stable system does not necessarily need a control. However,

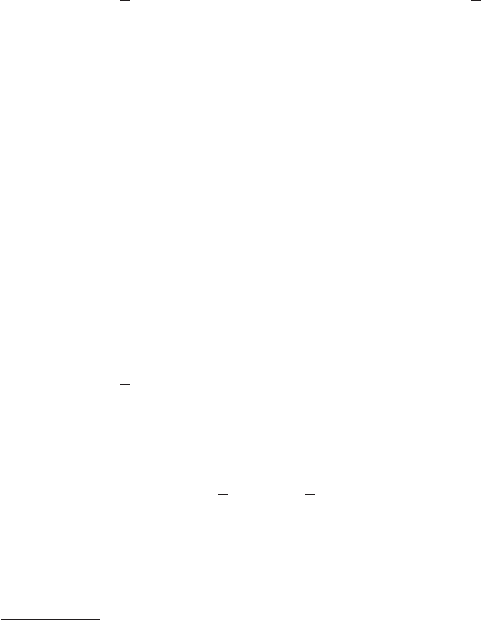
3.1 Introduction to Linear Quadratic Problems 71

in cases where the initially slightly disturbed system relaxes very slowly back

to the optimum trajectory, an additional control may support this process in

order to make this convergence faster.

3.1.4 The General Solution of Linear Quadratic Problems

Following the above-introduced concept, the linear quadratic problem consists

in the determination of the optimum control w

∗

, of the optimum trajectory

∗

which solve the evolution equations of the linear system

Y (t)=A(t)Y (t)+B(t)w(t) (3.41)

with the initial condition

Y (0) = Y

(3.42)

and which minimizes the performance functional

J[Y, w]=



dt [Y (t)Q(t)Y (t)+w(t)R(t)w(t)] +

Y (T )ΩY (T ) . (3.43)

Here, we have used a generalized representation of the version of (3.5)con-

sisting of an integral and an endpoint function. As mentioned in Sect. 2.2.2,

the minimization of this mixed performance is called a Bolza problem. The

additional consideration of the endpoint is a real extension against (3.5)inthe

framework of linear quadratic problems. This is not in contrast to the general

statement

that each endpoint functional can be transformed in an integral

representation. This is also possible in the present case, but then we obtain

an additional evolution equation which is not linear.

In principle, the problem is only a special case of the large class of de-

terministic control problems. This can be solved by the techniques discussed

in Chap. 2. Here, we use the Hamilton approach. To this aim we rewrite the

performance integral

J[Y, w]=





Y (t)



Q(t)Y (t)+w(t)R(t)w(t)



(3.44)

with



Q(t)=Q(t)+Ωδ (t − T ) and construct the Hamiltonian

H = P [AY + Bw] −



QY −

wRw (3.45)

with the generalized momentum P (t). Because the small control is not as-

sumed to be restricted, we obtain from ∂H/∂w = 0 the pre-optimal control

(∗)

= R

−1

P, (3.46)

See the discussion in Sect. 2.2.2.

72 3 Linear Quadratic Problems

and the preoptimized Hamiltonian now reads

(∗)

= PAY −



QY +

PBR

−1

P. (3.47)

From here, we obtain the canonical system of evolution equations for the

optimal control

∗

= AY

∗

+ BR

−1

∗

(3.48)

and

∗

= −A

∗



∗

. (3.49)

Now, we introduce the time-dependent transformation matrix G(t) connect-

ing momenta P

∗

(t) and the state vector Y

∗

(t)viaP

∗

(t)=−G(t)Y

∗

(t)and

substitute this expression in (3.49)

−

∗

− G

∗

= A

∗



∗

. (3.50)

From here, we obtain with (3.48)

∗

= −A

∗

−



∗

− GAY

∗

− GBR

−1

∗

= −A

∗

−



∗

− GAY

∗

+ GBR

−1

∗

, (3.51)

which means the problem is solved if we ﬁnd a matrix G(t) which satisﬁes the

equation

G + A

G + GA − GBR

−1

G = −



Q. (3.52)

Because of



Q(t)=Q(t)+Ωδ (t − T ) we conclude that for all t = T , the matrix

G(t) is a solution of

G + A

G + GA − GBR

−1

G = −Q. (3.53)

The equation is called the diﬀerential Ricatti equation with the boundary

condition

G(T )=Ω. (3.54)

which follows immediately from (3.52) by an integration over the time inter-

val [T − ε, T + ε]. The symmetry of (3.53) and (3.54) requires the symmetry

of G(t)=G

(t). Of course, (3.53) is a nonlinear system of N × N ordinary

coupled diﬀerential equations. Although a detailed analysis of (3.53)often

requires the application of numerical tools [4, 5, 7, 8], the diﬀerential Ri-

catti equation is usually considered to be the complete solution of the linear

quadratic problem.

Finally, we get the expression for the optimal control from (3.46),

∗

= −R

−1

∗

(3.55)

while the optimal trajectory follows from the homogeneous linear system of

diﬀerential equations

∗



A − BR

−1



∗

(3.56)

with the initial condition Y

∗

(0) = Y

. The linear relation between the current

state and control (3.55) is often called the control law. This law indicatesagain

3.2 Extensions and Applications 73

the above-suggested closed-loop character of the control mechanism because

the coupling between the control and state, R

−1

G, depends only on quan-

tities characterizing the dynamics of the system or the performance of the

control [5, 9].

3.2 Extensions and Applications

3.2.1 Modiﬁcations of the Performance

Generalized Quadratic Forms

We may extend the performance integral by adding a mixed bilinear term

Y (t)W (t)w(t). In principle, this idea corresponds to the intermediate stage

(3.3) of our heuristic derivation of quadratic linear problem. In the case of

empirically chosen matrices Q(t), R(t), and W (t), we must be aware that

this change can essentially modify the problem. In fact, the addition of such

bilinear terms can change the necessary positive deﬁnite structure of the per-

formance integral

J[Y, w]=





Y (t)



Q(t)Y (t)+w(t)R(t)w(t)+2Y (t)W (t)w(t)



. (3.57)

Therefore, these extension requires a further check of the composed matrix





, (3.58)

which must be positive deﬁnite for all times t ∈ [0,T].

Linear Quadratic Performance

The quadratic performance functional may be extended to a linear quadratic

functional by adding linear functions of the control functions and the state

variables into functional (3.43)

J[Y, w]=



dt [Y (t)Q(t)Y (t)+w(t)R(t)w(t)]



dt [α(t)Y (t)+β(t)w(t)]

Y (T )ΩY (T )+ωY (T ) . (3.59)

It is easy to check that in this case the optimum control is given by

74 3 Linear Quadratic Problems

∗

= −R

−1

[GY

∗

+ ξ]+β

, (3.60)

where G(t) solves the diﬀerential Ricatti equation (3.53) with the boundary

condition (3.54) while the newly introduced vector function ξ(t) solves the

following system of linear diﬀerential equations

ξ = −



A − BR

−1



ξ + GBR

−1

β − α, (3.61)

and the boundary condition

ξ(T )=ω. (3.62)

The optimal trajectory follows from a modiﬁed version of (3.56), namely

∗



A − BR

−1



∗

+ BR

−1

ξ. (3.63)

In principle, the derivation of (3.60) follows the same scheme as the derivation

of (3.55) in Sect. 3.1.4. The only diﬀerence is the application of the generalized

relation P

∗

(t)=−G(t)Y

∗

(t)+ξ(t) instead of P

∗

(t)=−G(t)Y

∗

(t).

Tracking Problems

Let us assume that we wish a certain, but small modiﬁcation ψ(t) of the op-

timum trajectory X

∗

(t), i.e., the desired ideal evolution of the system under

control is now given by X

ideal

(t)=X

∗

(t)+ψ(t), which means, we have to ask

for a small modiﬁcation w(t) of the control such that the actually realized tra-

jectory X(t)=X

∗

(t)+Y (t) is close to the ideal trajectory X

ideal

(t). In other

words, the control aim is to ﬁnd a trajectory which follows a given external

signal ψ(t). This can be done by considering the performance functional

J[Y, w]=



dt [(Y (t) − ψ(t)) Q(t)(Y (t) − ψ(t)) + w(t)R(t)w(t)]

(Y (T ) − ψ(T )) S (Y (T ) − ψ(T )) . (3.64)

This problem is a special case of a linear quadratic problem with a linear

quadratic performance with β(t)=0andα(t)=−Qψ. Therefore, we can

employ the results presented above. In particular, the optimal control of the

tracking problem is given by

∗

= −R

−1

[GY

∗

+ ξ] , (3.65)

where G(t) again solves the diﬀerential Ricatti equation (3.53) while the func-

tion ξ(t) is a solution of

ξ = −



A − BR

−1



ξ + Qψ (3.66)

with the boundary condition ξ(T )=−S. The optimal trajectory is given by

∗



A − BR

−1



∗

+ BR

−1

ξ. (3.67)

Tracking problems occur in several scientiﬁc problems. Typical examples are

electronic or hydraulic ampliﬁers, where an incoming signal is transformed

into a response signal with another amplitude and phase.