Schulz M. Control Theory in Physics and Other Fields of Science: Concepts, Tools, and Applications
Подождите немного. Документ загружается.


288 10 Optimization Problems
As a naive approach to such discrete optimization problems, we may solve
the corresponding continuous control problem. Then the obtained result is
approximated by that allowed discrete value of u which has the shortest dis-
tance to the optimal continuous result. However, this procedure fails often,
especially in the case of the so-called 0–1 optimization with only two values
per component u
α
.
An alternative way is the direct computation of the value of the optimiza-
tion function for all admissible states u. But this procedure needs an enormous
amount of computation time. For example, the 0–1 optimization requires 2
n
steps in order to compute the optimum.
A well-established theory exists for linear combinatorial optimization prob-
lems [23, 39, 40, 41, 42], for example branch and bound methods [43]ormod-
ified simplex methods
5
[44]. Most of these techniques require a computation
time which increases exponentially with increasing n. In the case that the
control space U consists of only a finite number of discrete values, the opti-
mization problem may be transformed into a 0–1 optimization problem. We
remark that these special problems are also denoted as binary optimization
or Bool’s optimization. The transformation can be realized via
u
α
=
L
α
k=1
u
(k)
α
s
k,α
(10.32)
where u
(k)
α
are the L
α
discrete values of the component u
α
while the s
k,α
takes
the values 0 or 1 under the constraint that
1=
L
α
k=1
s
k,α
(10.33)
The combinatorial optimization is strongly connected with the complexity
theory of algorithms. Here, the problems are classified with respect to the
expected computation times so that one speaks also of time-complexity. As
remarked above, the majority of the combinatorial optimization problems
belong to the class of nonpolynomial (NP) problems. That means the compu-
tational time increases with increasing n faster as a polynomial of finite order.
Some problems, for example the above mentioned modified simplex methods,
can be reduced to polynomial problems with a computation time T (n) ∼ n
a
with a finite exponent a. All other problems have computation times, e.g.,
given by 2
n
or n!. These problems are elements of the NP class. Formally, the
polynomial class is a subset of the NP class. This implies that all polynomial
problems can be always expanded to a NP problem by some algebraic manip-
ulations. But not all NP problems can be reduced to a polynomial problem.
In fact, there exists a special subset of the nonlinear problems which is defined
by the NP completeness. All problems of this NP complete set can be neither
5
It should be remarked that in principle the simplex method itself can be also
interpreted as a combinatorial optimization method.
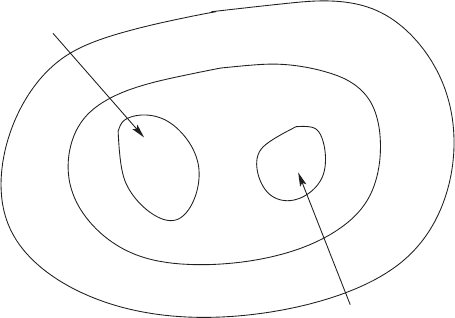
10.2 Optimization Methods 289
NP
NP complete
Decidable problems
Polynomial
Fig. 10.3. The relations between the different classes of time complexity
reduced to a polynomial problem nor transformed into another element of the
NP complete set with a computation time of polynomial lngth. Hence, both,
polynomial problems and NP complete procedures are embedded in the set of
NP problems (Fig. 10.3), but both classes are exclusive. We remark that the
set of nonpolynomial problems is a subset embedded in the set of decidable
problems.
10.2.5 Evolution Strategies
Evolution strategies [2, 4] are methods which are suggested by Darwinian
paradigm of evolution. Especially the principle of variation and selection can
be considered as the fundamental principle of the Darwinian theory. This
principle, combined with a reproduction procedure, builds up the fundamental
components of an evolutionary strategy.
The basic principle of evolution methods is quite simple. Let us assume we
have a set of M different admissible vectors u
(µ)
i
∈ G, i =1,...,M. The set of
the M quantities u
(µ)
i
is called the parent set. Then the corresponding values
H
(µ)
i
= H(u
(µ)
i
) are denoted as fitness values. The lowest (largest) value of
the set of H
(µ)
i
corresponds to the current estimation of the optimum. The
index µ indicates the generation of the evolution. Initially, we have µ =0and
the u
(µ)
i
are M (randomly) chosen quantities of the region G.
The first step of an evolution loop is the so-called recombination procedure.
There exist various techniques, e.g.
• Discrete recombination: two parent vectors, say u
(µ)
1
and u
(µ)
2
,oftheµth
generation are chosen randomly. Then we choose a diagonal n × n random
matrix R
1
with only 0 and 1 components, e.g.
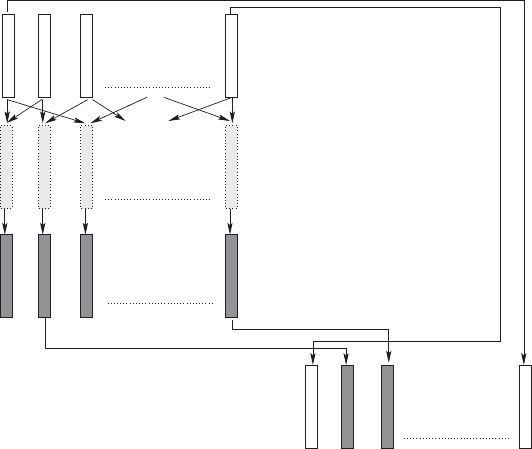
290 10 Optimization Problems
Selection
New parent set
Mutation
Pre-offsprings
Recombination
Parents
Offsprings
Fig. 10.4. The basic elements of evolutionary optimization strategies
R
1
=
10
.
.
.
00
.
.
.
0
.
.
.
.
.
.
1
.
.
.
0
.
.
.
.
.
.
0
.
.
.
00
(10.34)
while the dual matrix R
2
is given by
R
1
+ R
2
= 1 (10.35)
Then a so-called pre-offspring corresponding to the parents is given by
u
= R
1
u
(µ)
1
+ R
2
u
(µ)
2
(10.36)
If u
is also admissible, u
∈ G, the pre-offspring is collected in a set K;
otherwise it will be deleted.
• Intermediate recombination: two parents are chosen randomly, and the
weighted average
u
= λu
(µ)
1
+(1− λ)u
(µ)
2
(10.37)
with a randomly chosen parameter 0 ≤ λ ≤ 1 is the offspring. This recom-
bination procedure is always successful for convex sets G.
10.2 Optimization Methods 291
• Discrete multiple recombination: L “parents”, u
(µ)
α
1
,...,u
(µ)
α
L
, are chosen ran-
domly from the parent set. Furthermore, we choose L diagonal matrices of
type (10.34) satisfying
L
j=1
R
j
= 1 (10.38)
Then, the pre-offspring is given by
u
=
L
j=1
R
j
u
(µ)
α
j
(10.39)
i.e., each component of the pre-offspring vector u
is equal to the corre-
sponding component of one of its parents.
• Intermediate multiple recombination: L parents, u
(µ)
α
1
,...,u
(µ)
α
L
,andL real
numbers 0 ≤ λ
j
≤ 1 with the constraint
L
j=1
λ
j
= 1 (10.40)
are chosen randomly. The pre-offspring is then
u
=
L
j=1
λ
j
u
(µ)
α
j
(10.41)
which is especially admissible if G is a convex set.
After determination of a set of M
pre-offsprings, these quantities are (usu-
ally slightly) changed by a mutation step, i.e., a random vector correspond-
ing to a certain probability distribution (e.g., a Gaussian distribution or a
uniform distribution) is added to each pre-offspring. The result is offsprings
u
(µ)
1
,...,u
(µ)
M
. If some offsprings are no longer admissible, u
(µ)
j
/∈ G, another
offspring is formed by the repetition of the recombination and mutation step.
The common (M + M
) set of parents and offsprings,
9
u
(µ)
1
,...,u
(µ)
M
,u
(µ)
1
,...,u
(µ)
M
:
(10.42)
is now the input for the subsequent selection step. That means, we determine
the fitness, H(u
(µ)
i
)andH(u
(µ)
i
), respectively, of these components and select
the best M elements. These quantities are the M parents u
(µ+1)
i
of the next
generation.
The repeated application of this procedure should drive the set
9
u
(µ)
1
,...,u
(µ)
M
:
(10.43)
to the optimum for µ →∞, i.e., the lowest (largest) value of the corresponding
fitness indicates the optimal solution. We remark that this expected conver-
gence to the optimum solution is not guaranteed at all [2]. The simple (1 + 1)
evolution strategy (one parent, one offspring), i.e.
292 10 Optimization Problems
u
(µ+1)
= u
(µ)
+ ξ (10.44)
where ξ is an admissible random vector, corresponds to the stochastic proce-
dure discussed in Sect. 10.2.1. For more details and several applications we
refer to the literature [2, 4, 3].
References
1. K.H. Elster: Modern Mathematical Methods of Optimization (Akademie Verlag,
Berlin, 1993) 280
2. H.G. Beyer: The Theory of Evolution Strategies (Springer, Berlin Heidelberg
New York, 1998) 289, 291, 292
3. M. Delgado, J. Kacprzyk, J.-L. Verdegay, M.A. Vila: Fuzzy Optimization
(Physica-Verlag, Heidelberg, 1994) 292
4. B. Kost: Optimierung mit Evolutionsstrategien (Verlag Harri Deutsch, Frankfurt
A.M., 2003) 289, 292
5. C. Geiger, C. Kanzow: Theorie und Numerik Restrigierter Optimierungsauf-
gaben (Springer, Berlin Heidelberg New York, 2002) 283
6. C. Geiger, C. Kanzow: Numerische Verfahren zur L¨osung unrestrigierter Opti-
mierungsaufgaben (Springer, Berlin Heidelberg New York, 1999) 283
7. I. Bomze, W. Grossmann: Optimierung-Theorie und Algorithmen (Wis-
senschaftsverlag, Mannhein, 1993) 283
8. C. Richter: Optimierungsaufgaben und BASIC Programme (Akademie-Verlag,
Berlin, 1988) 283
9. P. Spelucci: Numerische Verfahren der nichtlinearen Optimierung (Birkh¨auser,
Basel, 1993) 283
10. E.J. Gumbel: Statistics of Extremes (Columbia University Press, New York,
1958) 284
11. G.K. Zipf: Human Behavior and the Principle of Least Effort (Addison-Wesley,
Cambridge, 1949) 284
12. J.W. Barret, G. Moore, P. Wilmott: Risk 5, 82 (1992) 284
13. R. Brotherton-Ratcliffe: Risk 7, 53 (1994) 284
14. K.-T. Fang: Number-Theoretic Methods in Statistics (Chapman and Hall, Lon-
don, 1994) 284
15. P. Hellekalek, G. Larcher: Random and Quasi-Random Point Sets (Springer,
Berlin Heidelberg New York, 1998) 284
16. C. Joy, P.P. Boyle: Manage. Sci. 42, 926 (1996) 284
17. J.X. Li: Revista de An´alisis Econ´omico 15, 111 (2000) 284
18. W.J. Morokoff: SIAM Rev. 40, 765 (1998) 284
19. H. Niederreiter, P. Hellekalek, G. Larcher, P. Zinterhof: Monte Carlo and Quasi-
Monte Carlo Methods (Springer, Berlin Heidelberg New York, 1996) 284
20. W.C. Snyder: Math. Comput. Simul. 54, 131 (2000). 284
21. H. Niederreiter: SIAM, CBMS 63, 241 (1992) 285
22. W. Krabs: Einf¨uhrung in die lineare und nichtlineare Optimierung f¨ur Ingenieure
(Teubner-Verlag, Leipzig, 1983) 286, 287
23. K.H. Borgwardt: Optimierung, Oparations Research, Spieltheorie (Birkh¨auser,
Basel, 2001) 287, 288
References 293
24. K. Glashoff, S. Gustafson: Linear Optimzation and Approximation (Springer,
Berlin Heidelberg New York, 1978) 287
25. K. Marti, D. Gr¨oger: Einf¨uhrung in die lineare und nichtlineare Optimierung
(Physica-Verlag, Heidelberg, 2000) 287
26. E. Seiffart, K. Manteufel: Lineare Optimierung (Teubner-Verlag, Leipzig, 1974) 287
27. A.K. Hartmann, F. Ricci-Tersenghi, Phys. Rev. B 66, 224419 (2002) 287
28. J. Houdayer, O.C. Martin: Europhys. Lett. 49, 794 (2000) 287
29. P. Palassini, F. Liers, M. J¨unger, A.P. Young: Phys. Rev. B 68, 064413 (2003) 287
30. A.K. Hartmann, H. Rieger: Optimization Problems in Physics (Wiley-VCH,
Berlin, 2002) 287
31. J. Houdayer, O.C. Martin: Phys. Rev. E 64, 056704 (2001) 287
32. M. J¨unger, G. Rinaldi: Relaxation of the max cut problem and computation of
spin-glass ground states. In: Operations Research Proceedings,edbyP.Kischka
(Springer, Berlin Heidelberg New York, 1998), p. 74 287
33. U.H.E. Hansmann, Y. Okamoto: J. Chem. Phys. 110, 1267 (1999) 287
34. S. Kirkpatrick, C.D. Gelatt, M.P. Vecchi: Science 220, 671 (1983) 287
35. Y. Duan, P.A. Kollman: Science 282, 740 (1998) 287
36. A. Buhot, W. Krauth: Phys. Rev. Lett. 80, 3787 (1998) 287
37. J.A. Cuesta: Phys. Rev. Lett. 76, 3742 (1996) 287
38. P.W. Kasteleyn, C.M. Fortuin: J. Phys. Soc. Jpn. 26, 11 (1969) 287
39. A. Brink, H. Damhorst, D. Kramer, W. Zwehl: Lineare und ganzzahlige Opti-
mierung mit impac (Vahlen, M¨unchen, 1991) 288
40. R.E. Burkhard: Methoden der ganzzahligen Optimierung (Springer, Berlin Hei-
delberg New York, 1972) 288
41. J. Piehler: Ganzzahlige lineare Optimierung (Teubner-Verlag, Leipzig, 1982) 288
42. J. Piehler: Algebraische Methoden der ganzzahligen Optimierung (Teubner-
Verlag, Leipzig, 1970) 288
43. E. Fischer, A. Stepan: Betriebswirtschaftliche Optimierung (Oldenbourg Verlag,
M¨unchen, 2001) 288
44. K. Neumann, M. Morlock: Operations Research (Carl Hanser Verlag, M¨unchen,
1993) 288
45. K. Marti: Stochastic Optimization Methods (Springer, Berlin Heidelberg New
York, 2005) 283
46. L.C.W. Dixon, E. Spedicato, G. Szeg¨o: Nonlinear Optimization (Birkh¨auser,
Boston, 1980) 283

Index
action 22, 201
activation function 256
active boundaries 117
adaptive memory 252
adaptive resonance network 259
adjoint field equation 113
adjoint state vector 38
adjoint evolution equation 38, 144
admissible trajectory 197
adsorbing boundaries 116
algebraic complexity 9
algebraic Ricatti equation 79, 146
anomalous propagator 183
anticausality 87
ARMA 249
ARCH 249
associative memory 258
asymptotic behavior 225
attractor 128
autonomous system 41, 130
autoregression 246
autoregressive process 247
average 161
balance equation 99
basic functions 114
Bayesian concept 249
Bayesian statistics 150
Bayes risk 269
Bayes theorem 250, 269
Belousov-Zhabotinskii reaction 11, 144
Bernoulli 17, 227
Berry-Ess´een theorem 222
bidirectional network 258
bifurcation 134
bilinear control 89
bilinear problem 276
binary optimization 288
biological organism 12
Bolza problem 20
boundary conditions 19, 94, 114
boundary control 116
bounded system 124
brachistochrone problem 17
Brownian particle 240
canonical transformation 57, 124
Cauchy law 225
causality 87
cellular automata 252
central limit theorem 215
channel 265
chaos 5, 123
chaotic trajectory 126
Chapman-Kolmogorov equation 169,
172, 195
characteristic function 163
characteristic polynomial 140
characteristic time 168
classical field theory 94
closed-loop control 2, 174
combustion 100
complex boundaries 50
complex constraints 50
complexity 6
complexity theory 288
296 Index
complete integral 57, 124
complex structure 6
complex system 6, 215
concave function 231
conditional periodic motion 125
conditional probability 165
conical function 68
constraints 20
control action 266
control aim 2
control equation 204
control function 2
controllability 139
control law 144
control variable 19
convex function 231
convex polyhedron 281
convex set 280
convolution 218
correlation function 177
correlation matrix 162
correlation time 177
cost functional 19
cost matrix 267
covariance matrix 164
Cram´er function 229
critical value 134
critical temperature 255
cumulant 163
current observation 246
cyclic boundary condition 141
Darwinian paradigm 289
decimation step 217
decision selection 250
decision theory 249
decrescent 69
degree of belief 149
degree of freedom 3
delayed feedback 142
destruction loss 227
determinism 4
deterministic chaos 4, 132
deterministic motion 174
deterministic series 284
deterministic strategy 272
developed turbulence 227
discrepancy 284
discrete equations 132
discrete recombination 289
differential constraint 20
differential operators 82
differential Ricatti equation 72
diffusion coefficient 203
diffusion-jump process 214
diffusion-limited process 102
Dirac’s function 37
discontinuous jumps 176
DuBois-Reymond 23, 26
Dulaque 66
dynamical matrix 82
dynamic phase transition 12
dynamic state 9
dynamic system 1
earth climate 7
earthquake 227
economic field theory 107
economic principle 108
economic systems 7
eigenvalues 66
embedded tori 125
endpoint functional 20
ensemble theory 149
entropy balance 100
ergodicity 6
ergodic curves 125
Euler-Lagrange equation 24, 94
events 151
evolution equation 10
evolution inequalities 51
excess kurtosis 164
external control 1
extremal 24
extremal evolution 37
extremal solution 279
extrem fluctuations 230
feedback control 194
feedback mechanism 2
feedback stochastic control 208
feedback strategy 79
Feigenbaum constant 134
Fermat’s law 111
financial markets 12
field 93
filter 233, 243
filter function 233
Index 297
filtered data 239
filtering problem 234, 244
first-order variation 22
fitness 291
fixed point 127
Floquet theory 142
fluctuating force 181
Fokker-Planck equation 175, 190
Fokker-Planck operator 206
forcasting equation 246
form stability 223
forsighted control 194
fractional calculus 85
fractional derivation 84
free boundary condition 35
frequency operator 159
Fredholm integral 88
free energy problem 279
frequency matrix 82, 180
functional 19
future evolution 246
future performance 204
Galilei 5
game theory 265
game symmetry 272
GARCH 249
Gaussian attractor 222
Gaussian function 217
Gaussian law 221
Gaussian process 232
Gaussian regime 228
generalized Lagrangian 36
generalized momentum 40
generalized momentum field 105
generalized quadratic form 73
general control problem 38
generating function 57, 163
Gibb’s distribution 253
Glauber dynamics 253
global maximum 280
Gnedenko 221
G¨odel 9
gradient-based algorithm 260
granular matter 7
Green’s function 114, 235
ground state 279
Gutenberg-Richter law 227
Hamilton’s equation 3
Hamiltonian 3, 41
Hamilton-Jacobi theory 55
Hamilton-Jacobi equation 124
Hamilton principle 33
harmonic oscillator 49
harmonic theory 82
heat exchange 89
Hebb rule 254
Hesse matrix 281
historical observation 246
homogeneous solution 114
Hopfield network 257
human brain 7
Huygens 144
hydrodynamic field 99
Hypothesis 249
induction motor 89
inequality constraints 51
inhomogeneous linear evolution 75
initial conditions 4
input 2
instable fixed point 64
integral equation 115
integral functional 20
integro-differential equation 159
intelligent player 274
intermediate recombination 290
intrinsic control 1
inverted pendulum 79
irrelevant degree of freedom 153
irrelevant variables 8
irreversibility 174
Ising model 287
isolated time points 51
isolated tori 125
isoperimetric problem 39
Ito equation 187, 199
Ito calculus 187
Ito’s formulae 189
Jacobi criterion 28
Jacobi trajectory 29
Jacobi zeros 29
joint probability 165, 216
jump process 176, 214
Kalman filter 232
298 Index
Kelvin model 101
kinetic equation 127, 174
kinetic energy 54
Klein-Gordon field 94
Kohonen network 258
Kolmogorov 150
Kolmogorov-Arnold-Moser theorem 126
Lagrange 23
lagrange method 285
Lagrange problem 20
Lagrange multiplier 35, 285
Lagrangian 22, 94
Langevin equation 185
Laplace transform 83
large fluctuations 228
layer structure 257
learning procedure 259
Legendre criterion 27
Legendre transform 230
L´evy function 224
L´evy regime 228
L´evy-Smirnow law 224
lexicographic order 275
limit cycle 128
linear combination 281
linear evolution 63
linear field equations 113
linear quadratic performance 73
linear quadratic problem 63, 210
linear stability 63
Liouville equation 153
Liouvillian 152
Ljapunov equation 237
Ljapunov exponents 4
Ljapunov function 68
Ljapunov’s first theorem 69
Ljapunov’s second theorem 70
location theory 107
logistic map 131
long-range correlation 178
long-run memory 85
Lotka model 127
macroscopic scales 8
many-player game 271
Marcienkiewicz 164
Markov approximation 183
Markov diffusion 175
Markov property 168
master equation 175
matching condition 219
maximum principle 42, 111
Maxwell equations 98
Maxwell model 101
mean value 161
mean value theorem 186
mechanical action 22
median 161
Meier problem 20
memory 103
memory matrix 181
memory operator 160
mesoscopic scales 8, 13
microscopic scales 8
microscopic state 9, 151
minimax problem 279
minimum program 9
mixing flow 4
molecular design 13
molecular dynamics 53
moment 162
momentum 40
momentum field 105
monomials 65
Mori-Zwanzig equation 179
most probable value 161
moving avarange 249
multiple observations 270
multiple recombination 291
multiplicative coupling 47
mutation step 291
Nahwirkungsprinzip 94
Nakajima 156
Nash 274
Nash equilibrium 276
natural excess 108
Navier-Stokes equation 100
nerve cell 252
network topology 259
neural networks 251
Newton 6
Newtonian friction 31
Newton learning algorithm 260
Newton’s procedure 283
nominal state 61
nominal trajectory 145
