Schlick T. Molecular Modeling and Simulation: An Interdisciplinary Guide

Подождите немного. Документ загружается.

200 6. Topics in Nucleic Acids Structure: DNA Interactions and Folding

Box 6.5: Elastic Constants and Persistence Length

As discussed in the text (eq. (6.5)), the elastic bending constant of DNA, A, can be

linearly related to the bending persistence length of DNA, p

,as:A = k

,where

is Boltzmann’s constant and T is the temperature. In addition, A can be related to the

root-mean-square (RMS) bending angle θ



1/2

of a semiﬂexible chain with a preferred

axis of bending (perpendicular to the helix axis), for which the angular ﬂuctuations are

independent from one another [694]:

A =(2k

Th)/θ

. (6.7)

Here h is the bp-separation distance in DNA (around 3.4

A) [491, 1095]. (Box 6.6 de-

scribes how θ

is related to the roll and tilt variables introduced earlier).

Similarly, the torsional rigidity constant can be related to the persistence length of

twisting p

and the RMS twist angle Ω as [830]:

C =(p

T)/2 (6.8)

and

C =(k

Th)/Ω

. (6.9)

For the bending to torsional rigidity constant ratio r = A/C, the relationship

Ω



1/2

= θ



1/2



(6.10)

follows.

The typical values for DNA (A =2.0 × 10

−19

erg cm and C =3.0 × 10

−19

erg cm)

correspond to persistence lengths for bending and twisting of p

= 500

A[491], p

750

A, and r =2/3. These values correspond to RMS bend and twist-angle values of

θ



1/2

=6.7

and Ω



1/2

=3.9

at room temperature, in the context of isotropic

bending. The bending constant A can also be related to measured local angular variations in

solved DNA structures, as detailed in Box 6.6. The torsional rigidity constant has recently

been estimated from pulling experiments on single molecules of DNA to be 40% higher

than generally accepted values [182].

6.7.3 Simulations of DNA Supercoiling

Many groups are studying the geometric, thermodynamic, statistical, and dy-

namical properties associated with supercoiling using a variety of models both

for representing the DNA and for simulating conformations. See, for example,

[103,107,108,145,231–233,512,577,656,657,697–699,830,939,947,1036,1036,

1052,1105,1119,1124,1127–1129,1144,1175,1211,1249,1250,1256,1274,1306–

1308,1308,1310,1311, 1339,1366,1410].

6.7. Computational Treatments of DNA Supercoiling 201

Box 6.6: Relationship between the DNA Bending Constant and Local Angular

Measurements in Solved Nucleic Acid Structures

To relate the elastic bending constant A and measured standard deviations of DNA

bending angles, the two components of bending — namely roll (ρ) and tilt (τ ), each with

associated stiffness constants A

and A

[943] — can be related to A via:

A =

ρ

 + τ



. (6.11)

As above, h is the bp-separation distance in DNA (around 3.4

A). By comparing the above

to eq. (6.7), we see that the bending persistence length of p

= 500

A corresponds to an

isotropic model where θ



1/2

=6.7

, as well as to an anisotropic bending model where

ρ



1/2

=5.7

and τ



1/2

=3.6

. Values from analysis of B-form crystal structures

yield somewhat smaller values for these roll and tilt ﬂuctuations (e.g., ρ



1/2

and

τ



1/2

) and thus a larger effective bending persistence length and rigidity constant

(by about 1.3,orA =2.6 × 10

−19

erg cm and p

= 500

A). However, the static ﬂuc-

tuations in the crystal structures do not directly correspond to the dynamic range of DNA

ﬂexibility.

For sufﬁciently small angular deﬂections, we can partition the total bending magni-

tude as

θ

 = ρ

 + τ

 =[k

Th(A

+ A

)]/(A

) . (6.12)

This ﬁrst-order model does not account for the well-recognized preferential direc-

tions of bending of DNA into the major and minor grooves with respect to other

directions [473, 940, 1096, 1285, 1454]. A non-uniform bending chain view is re-

quired for better representations, especially for sequences with intrinsic curvature, like

A-tracts.

A few of the many topics that have been studied using such models are the

behavior of supercoiled DNA as a function of salt [1125, 1309], solvent [1036],

superhelical density [1129],andlength[830, 1214, 1250]; extended theoretical

treatments based on elastic rod mechanics and dynamics [305, 651, 1175]; the

response of supercoiled DNA to constraints imposed by proteins [945]; theory

of elastic rods with applications to DNA [255, 256]; the geometry of DNA in

small minichromosome systems [834]; and the site juxtaposition time (the bring-

ing together in space of linearly-distant DNA segments due to supercoiling)

[607, 1211, 1310]. See Boxes 6.4 and 6.7 for examples of nucleosome folding

and site juxtaposition studies, respectively, as well as corresponding Figures 6.12

and 6.14–6.15 and related experimental studies of EM and nucleosome interaction

measurements [483].

Many models for studying nucleosomes and oligonucleosome arrays have also

been developed (e.g., [64, 108, 353, 883, 1219, 1240, 1312, 1441]) and should of-

fer further insights into the nature of the complex folding and dynamics of the

chromatin ﬁber.

202 6. Topics in Nucleic Acids Structure: DNA Interactions and Folding

0 1 2 453 6 7 8 9 10

1.6 ms

3.4 ms

4.2 ms4.0 ms

2.4 ms

3.0 ms

1.8 ms 2.0 ms 2.2 ms 2.6 ms

3.8 ms

2.8 ms

3.2 ms

time (ms)

, kb

bp 1

bp 900

3.6 ms

= 0.2 M

= −0.06

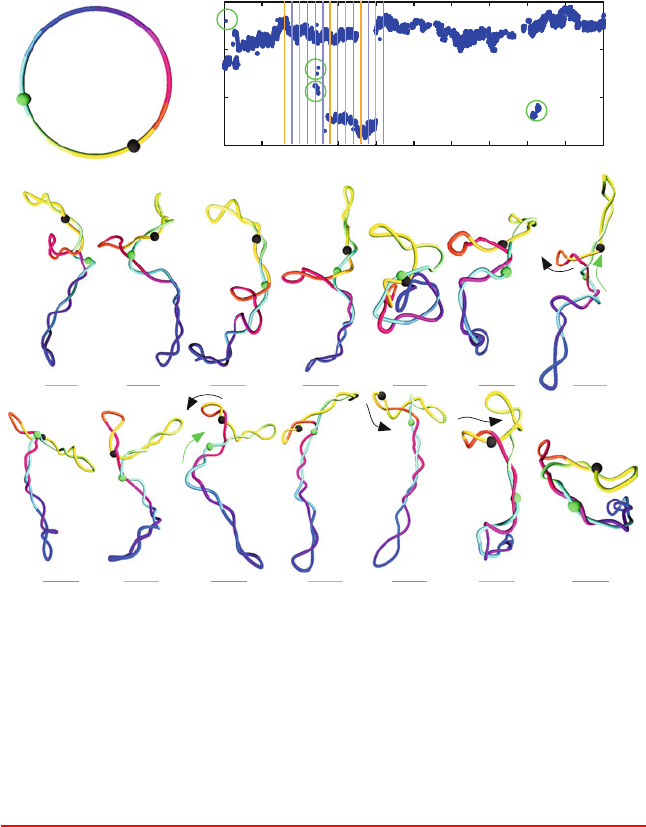
Figure 6.14. Juxtaposition kinetics, as analyzed for two beads separated by 900 bps in

circular DNA of length 3000 bps and σ = −0.06 by Brownian dynamics simulations at

high salt (c

=0.2 M sodium ions) [577]. (Top) Juxtaposition event plot, showing bps

that juxtapose with bp 1; the circled values correspond to more random juxtaposition

events, as illustrated for the snapshot at 2.4 ms. (Bottom) BD snapshots, showing ordered

motions along the DNA contour and rarer random collision events.

Box 6.7: Simulations of DNA Site Juxtaposition

Illustrative results from computer simulations of supercoiled DNA are shown in

Figure 6.14. These snapshots are taken from a Brownian dynamics simulation of a 3000-bp

DNA system at the superhelical density of σ = −0.06 at high salt using a homogeneous

bead/wormlike model [577]. Simulations have tabulated the times for distant sites to juxta-

pose due to the ambient ﬂoppiness of DNA as a function of the superhelical density, DNA

length, site separation, and the salt concentration [607].

6.7. Computational Treatments of DNA Supercoiling 203

0 0.02 0.04 0.06

〈T

〉 (ms)

0 0.01 0.02

= 0.01 M

= 0.2 M

0 0.02 0.04 0.06

100

Reaction, normalized %

synapsis

SIMULATION DATA

EXPERIMENTAL DATA

L = 3000 bp

= 600 bp

|s |

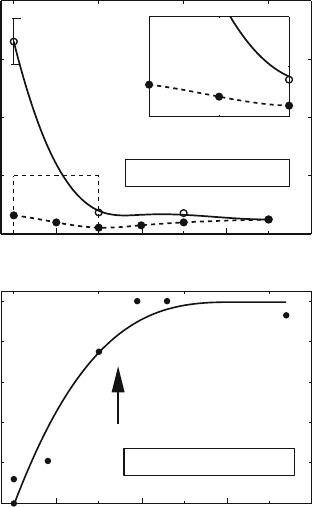
Figure 6.15. (Top): Site juxtaposition time measurements, T

, deﬁned as the mean time

for two sites d

bps apart to come within 100

A, as averaged over all such separated pairs,

as a function of |σ| for d

= 600 bps for a 3000 bp system and two salt concentrations

[577]. The inset focuses on the large salt effect at low |σ|. Note also the plateauing effect

of T

 around |σ| =0.03 for both salt concentrations. This is also the experimental

observation (bottom)[119] for the synapsis-time dependence on the superhelical density.

In the study of juxtaposition, two linearly-distant sites are considered juxtaposed when

the distance between them is 100

A or less. Interestingly, we ﬁnd (Figure 6.15)thatatlow

salt [608] juxtaposition times are accelerated by a factor of 10 or more due to supercoiling

(i.e., juxtaposition times for relaxed DNA are much slower), but that supercoiling beyond

|σ| =0.03 does not accelerate such site synapsis times [608]. Such critical behavior at

moderate |σ|agrees with experimental ﬁndings regarding supercoiling-dependent synapsis

rates for the resolvase recombination system [119], as also displayed in Figure 6.15.The

explanation for the fact that further supercoiling does not enhance juxtaposition times

signiﬁcantly emerges from our simulations: the balance between ﬂexibility and tight su-

percoiling is optimized at this mean value of superhelicity.

At high salt, the effect of superhelicity is far less dramatic. Further analysis of the mech-

anism for juxtaposition shows that large conformational rearrangements due to Brownian

motion operate at low superhelical density and low salt, whereas systematic slithering mo-

tions (reptation, or bidirectional conveyer-like motion) along the polymer contour [118]

are more prominent at high salt, as shown in Figure 6.14. At high salt, site juxtaposition

204 6. Topics in Nucleic Acids Structure: DNA Interactions and Folding

can be described by a combination of slithering, branch rearrangements, and interbranch

collisions, as also shown in the ﬁgure. The ﬁgure, prepared for studying site juxtaposition

kinetics [577], shows at top a plot in time of the bp i

that juxtaposes with the ﬁrst bp (i.e.,

is within 100

A of it). The continuous pattern in i

in time indicates ordered slithering; at

low salt, the patterns are much more random.

Topics in Nucleic Acids Structure:

Noncanonical Helices and RNA

Structure

Chapter 7 Notation

YMBOL DEFINITION

α polynucleotide backbone torsion angle

polynucleotide backbone torsion angle

glycosyl (sugar/base) torsion angle

Anything that DNA can do, RNA can do better.

Susan Gottesman, Cold Spring Harbor symposium, 2006.

7.1 Introduction

This chapter builds upon nucleic acid concepts introduced in the prior two

chapters to include a description of alternative hydrogen bonding schemes in

nucleic acids, non-canonical helical and hybrid structures, DNA mimics, over-

stretched and understretched DNA, and RNA structure and folding, including

secondary and tertiary-structure RNA modeling.

Besides the excellent texts [139, 195, 1080, 1191], the reader is invited to ex-

plore the wealth of related structural data on the nucleic acid database NDB

T. Schlick, Molecular Modeling and Simulation: An Interdisciplinary Guide, 205

Interdisciplinary Applied Mathematics 21, DOI 10.1007/978-1-4419-6351-2

 Springer Science+Business Media, LLC 2010

206 7. Topics in Nucleic Acids Structure: Noncanonical Helices and RNA Structure

(ndbserver.rutgers.edu/) and the protein data bank/research collaboratory for

structural bioinformatics (PDB/RCS) resource [128,1365], as well as information

concerning RNA on the RNA Ontology Consortium (ROC) [735].

As in the previous chapter, we abbreviate base pair and base pairs as bp and

bps, respectively.

7.2 Variations on a Theme

As evident from the previous chapter, nucleic acids are extremely versatile. The

classic right-handed double helical structure described by Watson and Crick is

an excellent textbook model. In Nature, however, polynucleotide helices have

developed an enormous repertoire of sequence-dependent structures, helical

arrangements, and folding motifs on both the bp and higher level of folding.

7.2.1 Hydrogen Bonding Patterns in Polynucleotides

Hydrogen-bonding variations are important for DNA’s adaptability to base mod-

iﬁcations (e.g., methylation, drug or carcinogen binding), bp mutations and

mismatches, and various interactions between DNA and proteins and among

polynucleotide helices.

Classic Watson-Crick (WC)

The classic WC hydrogen-bonding arrangement as shown in Figure 5.3 of

Chapter 5 is a particularly beautiful arrangement. It can be appreciated by not-

ing that the C1



(pyrimidine) to C1



(purine) distance is around 10.6

A in both the

AT and GC pairs, in good preparation for helix stacking. The intrinsic energy of

hydrogen bonds — that is, relative to vacuum — is generally in the 3–7 kcal/mol

range but only up to 3 kcal/mol in nucleic acids due to geometric constraints.

Though much weaker than covalent bonds (80–100 kcal/mol) [1191, p. 12–14],

the cumulative effect in the double helix is substantial due to the collective im-

pact of hydrogen-bonding interactions resulting from cooperative effects [1018].

Based on theoretical studies, the strength of the hydrogen-bond energy depends

on base composition but is very similar for the two WC bps. The energy of bp

stacking, 4–15 kcal/mol, substantially contributes to overall helix stability and

depends on the nucleotide sequence [169].

Yet, hydrogen-bonding patterns in polynucleotides are extremely versatile.

There are several nitrogens and oxygens on the bases, allowing various donor and

acceptor combinations involving different interface portions of the aromatic rings.

Estimates of base-pairing energetics in solvated nucleic acids come mainly from theoretical cal-

culations [1225]. This is because the resolution of macromolecular thermodynamic measurements into

subcontributions (hydrogen bonding, stacking, and electrostatic forces) remains a challenge, despite

numerous thermodynamic studies on nucleic acid systems [169, 449, 1007].

7.2. Variations on a Theme 207

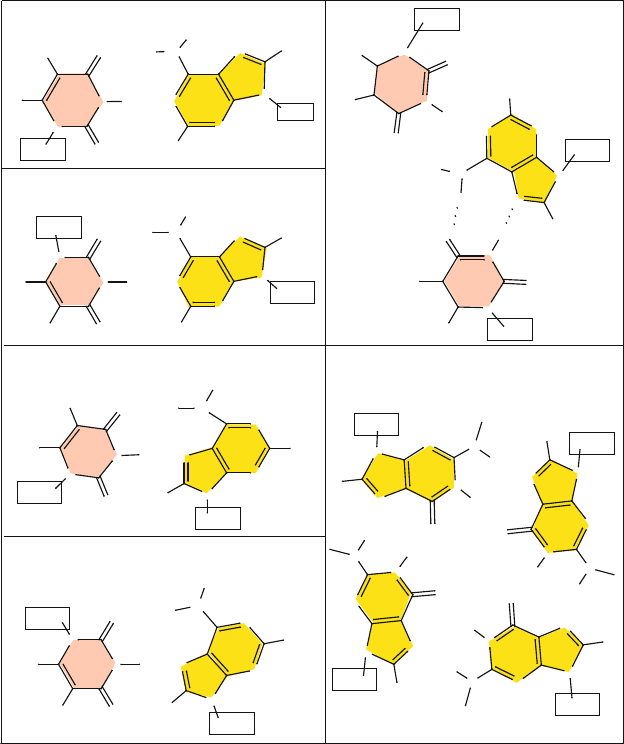
To appreciate this versatility, we ﬁrst examine the classic WC pattern in detail.

For an AT pair, two hydrogen bonds form between the C4–N3 face of T

and the C6=N1 face of A (see Figure 5.3 of Chapter 5 and Figure 7.1 here).

One hydrogen bond involves the sequence O4 (T)···H–N6 (A), i.e., between

the thymine carbonyl oxygen O4 attached to ring atom C4 and the adenine N6

atom, which is attached to the ring C6 atom. The other hydrogen bond is N3–H

(T)···N1 (A), between the thymine ring nitrogen N3 and the adenine N1.

For the GC pair, three hydrogen bonds form between the C4=N3–C2 face of

C and the C6–N1–C2 face of G: N4–H (C)···O6 (G), N3 (C)···H–N1 (G), and

O2 (C)···H–N2 (G). All hydrogen-bond lengths in both the AT and GC bps are

very similar, with individual lengths ranging from about 2.85 to 2.95

A between

the heavy atoms.

Reverse WC

Reverse WC base-pairing schemes can result when one nucleotide rotates 180

with respect to its partner nucleotide, as shown in Figure 7.1. Thus, one hydrogen

bond from the original WC scheme might be retained, but another can involve

a different atom combination. This ﬂip of one bp changes the position of the

glycosyl linkage. Hence, an AT pair can more easily accommodate this ﬂip due to

near symmetry about the N3–C6 axis of T. That is, since the ring face C4–N3–C2

of T has carbonyl attachments at both C4 and C2, the hydrogen bonding face can

be changed from C4–N3 to C2–N3 (see Figure 7.1). This type of reverse WC base

pairing exists in parallel DNA [1080].

Hoogsteen

Hoogsteen bps utilize a different part of the aromatic ring for hydrogen bonding.

Speciﬁcally, the N7–C5–C6 face of A and G, where N7 is in the 5-membered

ring and C6 is in the 6-membered ring of the purine, is used in the Hoogsteen

arrangement (see Figure 7.1). This is instead of the C6=N1 face of A and G —

both atoms of which are in the 6-membered ring of the fused-ring compound —

in combination with the C4–N3 face of T and C — as in WC interactions.

The Hoogsteen arrangement also implies a change in the glycosyl torsion angle

χ, from anti to syn, and a shortening of the C1



–C1



distance, from about 10.5

in WC to about 8.5

A in Hoogsteen base pairs (e.g., [12]).

Hoogsteen base pairing helps stabilize structures of highly bent DNA (e.g.,

TATA elements [971]), tRNAs, and DNA triplexes where two strands are held

by WC hydrogen bonds and where two strands are stabilized by Hoogsteen-type

pairing (see Figure 7.1). They also appear occasionally in complexes of DNA with

anti-cancer drugs. Recently, an unusual Hoogsteen A–T bp was discovered in a

high-resolution complex of unbent DNA bound to 4 MATα2 homeodomains (see

Figure 7.2)[12, 13].

208 7. Topics in Nucleic Acids Structure: Noncanonical Helices and RNA Structure

Sugar

Watson-Crick

Reverse Watson-Crick

Hoogsteen

Reverse Hoogsteen

4 3

Sugar

C O4

Sugar

C O4

Sugar

. . .

Triplex

Sugar

Guanine Quartet

. . .

Sugar

. . .

. .

Sugar

Hoog

Figure 7.1. Various hydrogen-bonding schemes: (left) classic Watson-Crick, reverse

Watson-Crick, Hoogsteen, and reverse Hoogsteen in base pairs; (right) WC/Hoogsteen

in a triplex (from an H-DNA structure, which forms in sequences that have stretches of

purine followed by stretches of pyrimidines, PDB code 1B4Y) [1290], and patterns in a

guanine-quartet quadruplex (or guanine tetraplex, PDB code 1JB7) [569].

Reverse Hoogsteen

Similarly, a reverse Hoogsteen arrangement involves the ﬂipping of one nucleo-

tide by 180

with respect to its partner, by analogy to reverse WC, as shown in

Figure 7.1.

7.2. Variations on a Theme 209

C G

G C

C G

A T

C G

A T

T A

A T

C G

T A

A T

T A

G C

T A

A T

C G

Hoogsteen

base pair

Figure 7.2. Unusual DNA/protein complex in which a Hoogsteen A–T base pair is found

in unbent DNA. The complex is a high-resolution crystal of four MATα2 homeodomains

bound to DNA [12,13].

Mismatches and Wobbles

Other bp arrangements involve anti/syn bps between two purines (a mismatch),

in which one base adopts an atypical syn glycosyl conﬁguration. This type of

pairing can occur due to protonation of one base (favored at acidic conditions) or

keto-enol tautomerizations. (See introduction to the term in Chapter 1, subsection

on the discovery of DNA structure, and Chapter 5, subsection on nitrogenous

bases).

Such ionized bases reverse the polarity of the hydrogen-bondingsites and hence

lead to various hydrogen-bonding schemes, such as between G

·C (Hoogsteen)

or the ionized mispair A

·C(wobble). Wobble pairs are formed when one base