Schlick T. Molecular Modeling and Simulation: An Interdisciplinary Guide

Подождите немного. Документ загружается.

230 7. Topics in Nucleic Acids Structure: Noncanonical Helices and RNA Structure

junction

bulge

loop

stem

Tree

Dual

edge vertex

vertex

edge

vertex

junction

bulge

loop

stem

vertex

stem

2bp

1bp

bulge

loop

We consider:

Translating RNA motifs to

graph theory objects

Leadzyme

Tree Graphs

Dual Graph

B1B3 B4

tRNA

Figure 7.11. Graphic Representations of RNA Secondary Structures shown for two RNAs,

using Tree and Dual Graphs, using the deﬁnitions at right [388, 438].

holds promise in the area of RNA structure analysis. Graph theory is suitable for

RNA because this ﬁeld of mathematics is widely used for analyzing networks

and enumerating structural possibilities, including chemical structures, genetic

and biochemical networks, monetary transactions, terrorist organizations, social

networks, and the Internet [33,900]; see also the 24 July 24 2009 issue of Science,

volume 325, devoted to networks.

Graph theory can be used to represent RNA secondary structures as two types

of graphical objects: trees and dual graphs according to speciﬁed rules for deﬁn-

ing RNA stems, bulges, junctions, and loops (Fig. 7.11). All possible RNA 2D

structure motifs, as simpliﬁed by this approach, can then be cataloged by the

graph vertex number, as well as ranked by topological complexity according to

the second-smallest eigenvalue of the Laplacian matrix of the graph [388,438].

7.5.2 RNA-As-Graphs (RAG) Resource

One such RNA topology resource, RAG (RNA-As-Graphs) (http://monod.

biomath.nyu.edu/rna), is being used to classify/analyze topological character-

istics of existing RNAs [438, 645](seeFig7.12 for graph enumeration segments

from RAG) and to design and predict novel RNA motifs [643–646]. See also some

RNA reviews commenting on graph theory applications to RNA [542,736].

Speciﬁcally, RAG and the associated graph theory framework for RNA [388,

435] have been used to classify and catalog RNA motifs [438, 645], esti-

mate the size of RNA’s structural/functional repertoire [645], detect structural

7.5. Application of Graph Theory to Studies of RNA Structureand Function 231

and functional similarity among existing RNAs [965], identify RNA motifs of

antibiotic-binding aptamers (found synthetically) in genomes [702–704], analyze

the structural diversity of random pools used for in vitro selection of RNAs [450],

simulate aspects of the process of in vitro selection in silico [643, 644, 646],

and analyze RNA thermodynamics landscapes to better understand riboswitch

mechanisms to ultimately enhance their design [1028].

Other applications of RAG in the community which include graph theory ex-

tensions involve classiﬁcation and prediction of ncRNAs [503,633,801,901,902,

1181], various RNA structure analyses [50,78,148,170,533,534,538,982,1041],

and various applications of graph theory [82,416,470,471,538,761,1324,1431].

Examples of graph extensions include labeled dual graphs [633] and directed

tree graphs [503]. Our application of spectral theory to catalog RNA graphs

has also been extended to other biological and physical systems [82, 416, 470,

471,761,1324,1431]. See Kim’s thesis for a more detailed descriptions on these

applications [642].

RNA Structure Enumeration

Cataloging based on graph theory enumeration suggests that the RNA structure

universe is dominated (more than 90%) by pseudoknots, in agreement with avail-

able data [645], as also discussed in [78,170,982,1041]. Signiﬁcantly, the existing

RNA classes represent only a small subset of possible 2D RNA motifs as enumer-

ated by graph index; some of these motifs may be natural while others may be

possible to generate in the laboratory. Still, others may not exist.

RNA-Like Motifs

The usage of clustering techniques to separate graphs that are ‘RNA-like’ from

those that do not resemble natural RNAs also led to predictions of many new

RNA-like motifs, including ten speciﬁc examples of sequences that might lead

to novel-like RNA topologies [645], as shown in Figure 7.13. Some of these

motifs predicted in 2004 have since been solved: C1 in mammalian CPEB3 ri-

bozyme [1084], C2 in a purine riboswitch [819], C3 in the tymovirus/Pomovirus

tRNA-like 3



UTR element [840], C4 in the tombusvirus 3



UTR region IV [1463],

and C7 in the ﬂavivirus DB element [235]. Signiﬁcantly, the predicted and actual

sequences have between 45 to 51% homology.

Graph theory tools are also natural for comparing RNA structures to ﬁnd ex-

isting RNA motifs within large RNAs based on graph isomorphisms [965]. This

idea was applied to identify topological similarities among existing RNA classes

and to deﬁne motifs of RNA within larger RNA topologies for major RNA classes

(e.g., tRNA, tmRNA, hepatitis delta virus RNA, 5S, 16S, 23S rRNAs).

Furthermore, the representation of RNAs as graphs led to identiﬁcation of RNA

motifs in genomes. Since natural aptamers exist in many bacterial genomes and

other organisms, it appeared likely that natural counterparts of synthetic motifs

exist in vivo. This led to development of an efﬁcient search tool for identifying

small RNA motifs in genomes by exploiting many artiﬁcial motifs derived from

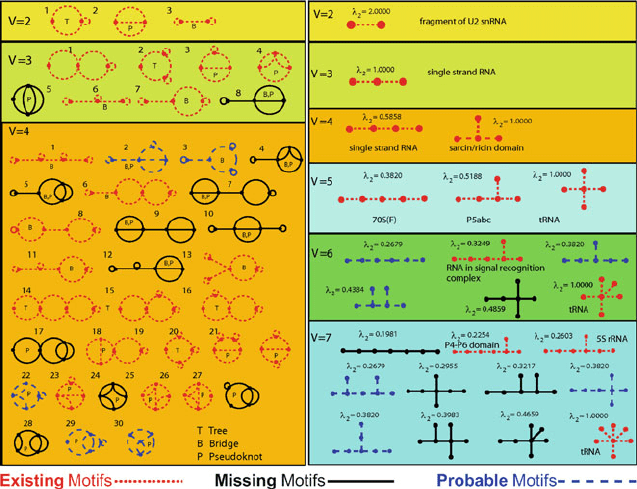
232 7. Topics in Nucleic Acids Structure: Noncanonical Helices and RNA Structure

Figure 7.12. Segments from RAG showing some enumeration of graphs for tree and dual

segments of low V numbers. The graphs are coded according to motifs found in nature

(red), motifs not yet found that are RNA-like (blue), as determined by clustering analysis,

and remaining motifs (black) [645]. See RAG website for details and updates.

RNA in vitro selection experiments [702–704]. The search for antibiotic-binding

aptamers produced 37 candidate sequences from bacterial and archaeal genomes.

RNA Design

Finally, graph theory tools can also advance the design of novel RNAs by

mimicking the process of in vitro selection in silico. As a ﬁrst step, understand-

ing the structural diversity of random pools was important for improving in vitro

technology. It is simple to generate random pools computationally, but graph

theory allowed rapid analysis of the resulting 2D motifs using 2D folding al-

gorithms [450]. By characterizing the distribution of secondary structure motifs

in computer-generated random pools using sets of possible RNA tree structures

from graph theory [450], we showed that random pools do not have a uniform

distribution of possible topologies and instead favor simple topological motifs.

This was expected from experimental observations that typically yield simple mo-

tifs. Further studies also found that the proportion of multiply branched structures

increases with sequence length, in agreement with other studies.

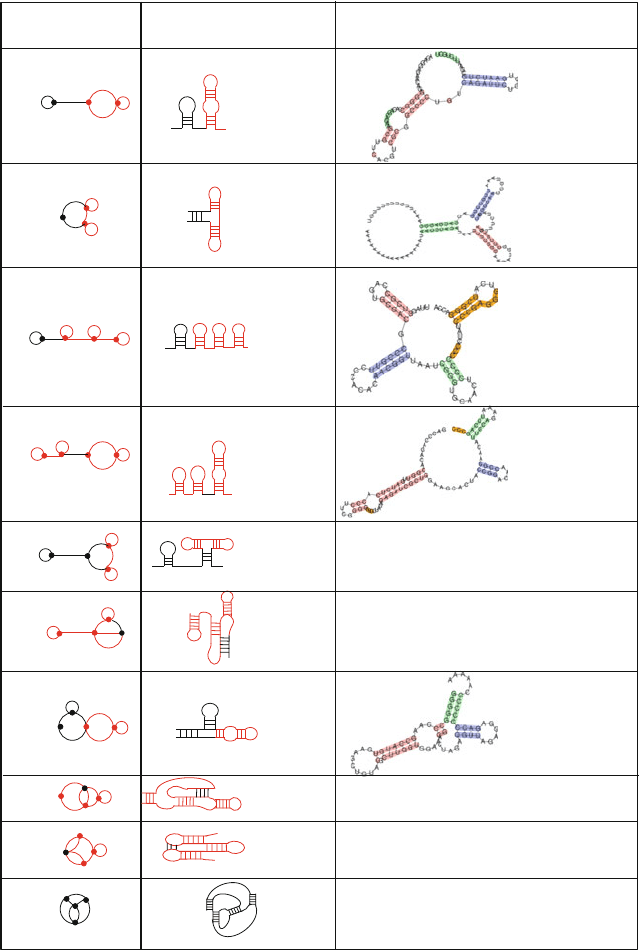
7.5. Application of Graph Theory to Studies of RNA Structureand Function 233

single strand RNA

(NDB:PR0055)

bulged hairpin

(Rfam:CopA)

DsrA RNA

(Rfam:DsrA)

single strand RNA

(NDB:PR0055)

bulged hairpin

(Rfam:CopA)

single strand RNA

(NDB:PR0055)

C10

DsrA RNA

(Rfam:DsrA)

bulged hairpin

(Rfam:CopA)

single strand RNA

(NDB:PR0037)

DsrA RNA

(Rfam:DsrA)

Flavivirus DB element

(Rfam:RF00525)

Purine Riboswitch

(Rfam: RF00167)

Tymovirus tRNA-like

3' UTR element

(Rfam: RF00233)

Candidates Discovered After 2004

RNA Secondary Structure With

Natural Submotif

Graph Representation

With Natural Submotif

Tombuvirus

3' UTR region IV

(Rfam: RF00176)

Mammalian CPEB3 Ribozyme

(Rfam: RF00622)

Figure 7.13. Ten candidates predicted to have RNA-like topologies, as determined by clus-

tering analysis, represented as dual graphs; the red submotif occurs in natural RNAs [645].

Of those ten, ﬁve RNAs were discovered since the published predictions, as shown in the

third column.

234 7. Topics in Nucleic Acids Structure: Noncanonical Helices and RNA Structure

4x4 mixing matrix M

RNA sequences

ACGUAGGGACCGUUU

UAAUAGGGACUACUU

UCCCUAGGGUACUAG

UACUGUAGUACUUAC

UCAGUUUUGGGGUAA

AAUAAUGAACUGACG

ACUGACCCUACGUAC

CAUGAUUUACGAUAC

~ 10

MMM

MMMM

Aptamers

Task

1. Specifying

sequence

mutations

Chemical probing

with functional assays

2. Generating

nucleotide

pools

3. Characterizing

structure and

function of

sequences

4 vials containing

A, C, G, and U

2D folding of sequences,

analysis of graph motifs

Initial

Structure

Candidate aptamer

sequences

Experiment Theory

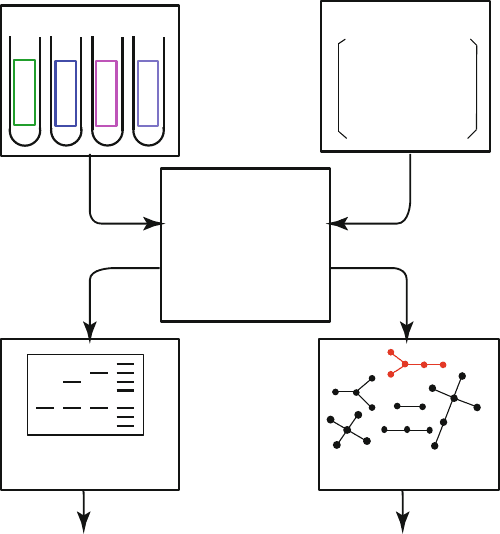
Figure 7.14. Experimental RNA pool synthesis and an in silico approach to mimic the pro-

cess [643,646]. Pool generation can be simulated using the mixing matrix, which speciﬁes

nucleotide mixtures in synthesis port or mutation rates for all nucleotide bases and can be

deﬁned to mimic speciﬁc biological situations [646]. The resulting sequences are “folded”

into 2D structures using existing algorithms and analyzed further to screen and ﬁlter the

candidates.

Mimicking the experimental process in silico can be done on the basis of

a “mixing matrix” framework (see Fig. 7.14), which led to development of

RAGPOOLS, a publicly-available web server for pool design [643]. Such mixing

matrices specify the mixing ratios of nucleotides in synthesis ports (see Fig. 7.14).

When applied to a starting sequence, each mixing matrix will generate a pool of

speciﬁc sequences via mutations of the given sequence. Thus, different design

strategies (based on covariance mutations like AU to CG or conversion of AU to

CG base pairs) produce different sequence pools, and the main idea is to design

these pools to yield the desired structure and/or function.

Using this new tool and other computational and experimental resources,

very large pools of nucleotides (up to 10

) can be generated, screened, and

ﬁltered according to various 2D-structure similarity and ﬂanking sequence

7.5. Application of Graph Theory to Studies of RNA Structureand Function 235

analyses [644]. Such computational and theoretical yields agree for simple RNA

motifs. For real aptamer targets, the in silico procedure overestimates the yields

found experimentally, as expected, because experimental yields represent lower

bounds and the screening does not yet involve 3D structural aspects.

Advances on all these fronts are ongoing.

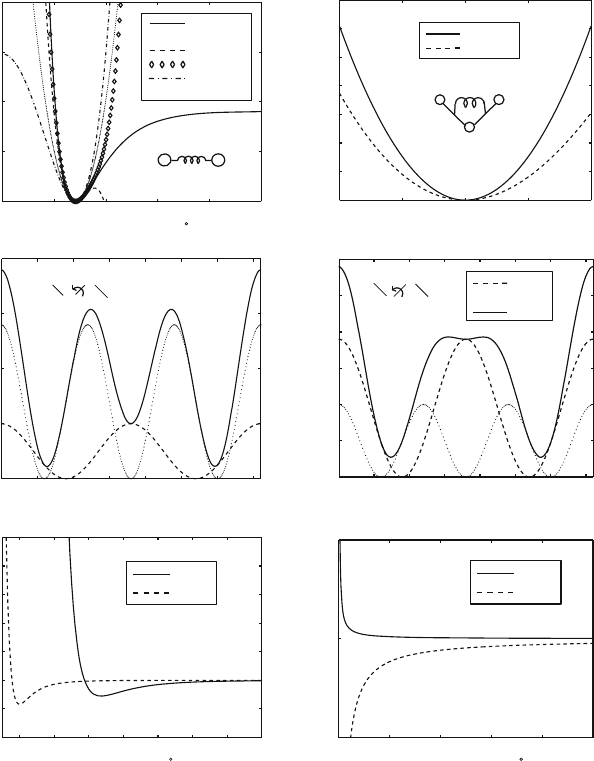
236 7. Topics in Nucleic Acids Structure: Noncanonical Helices and RNA Structure

2 3 4 5 6 7 8 9

−0.2

−0.1

0.1

0.2

0.3

0.4

0.5

50 100 150 200 250 300 350

0.5

1.5

2.5

50 100 150 200 250 300 350

0 1 2 3 4 5

100

150

200

Morse

Quartic

(special)

Cubic

...........

Quartic

Harmonic

r (bond length) [A]

Bond energy [kcal/mol]

2 fold

3 fold

sum

.........

(dihedral angle) [deg.]

Dihedral angle energy [kcal/mol]

O3'

C3'

C2'

O2'

O5'

C5'

Coulombic energy [kcal/mol]

LJ Energy [kcal/mol]

C...C

O...H

110 115 120 125 130

0.2

0.4

0.6

0.8

1.2

1.4

(bond angle) [deg.]

Bond Angle energy [kcal/mol]

Harmonic

Trig.

(dihedral angle) [deg.]

0 0.1 0.2 0.3 0.4 0.5

−5000

5000

r (distance) [A] r (distance) [A]

C...C

O...H

Dihedral angle energy [kcal/mol]

Theoretical and Computational

Approaches to Biomolecular Structure

Chapter 8 Notation

YMBOL DEFINITION

Vectors

a, b, c interatomic distance vectors (in deﬁnition of τ)

, n

unit normals

interatomic distance vector (x

− x

)

position vector of vector i, components x



collective momentum (for nuclei and electrons)



collective position (for nuclei and electrons)

collective position (nuclei only), components

,...,x

∈R

V collective velocity (nuclei only)

eigenfunctions of the Hamiltonian operator

Scalars & Functions

bond length i

Coulomb partial charge for atom i

interatomic distance (between atoms i and j)

initial time

Lennard-Jones coefﬁcients



Hamiltonian operator (E

+ E

)

bond

bond length energy

bang

bond angle energy

coul

Coulomb energy

kinetic energy

local

local (short-range) energy

eigenvalues of the Hamiltonian operator (quantum states)

nonlocal

nonlocal (long-range) energy

potential energy (also E)

T. Schlick, Molecular Modeling and Simulation: An Interdisciplinary Guide, 237

Interdisciplinary Applied Mathematics 21, DOI 10.1007/978-1-4419-6351-2

 Springer Science+Business Media, LLC 2010

238 8. Theoretical and Computational Approaches to Biomolecular Structure

Chapter 8 Notation Table (continued)

YMBOL DEFINITION

tor

torsional (dihedral) angle energy

Lennard-Jones energy

ijk

bond angle force constant

dimension of the Fock matrix

number of atoms

number of electrons

Euclidean space of dimension n

bond length force constant

set of bonds

set of bond angles

set of dihedral angles

set of atom pairs computed in the nonbonded energy

temperature

torsional barrier height of periodicity n



dielectric function

or θ

ijk

bond angle (e.g., θ

dha

for donor–hydrogen···acceptor

sequence in a hydrogen bond)

or τ

ijkl

dihedral or torsion angle

Δt

timestep

Science says the ﬁrst word on everything, and the last word on

nothing.

Victor Hugo (1802–1885).

8.1 The Merging of Theory and Experiment

8.1.1 Exciting Times for Computationalists!

Computational techniques for exploring three-dimensional (3D) structures of nu-

cleic acids and proteins are now well recognized as invaluable tools for revealing

details of molecular conformation, motion, and associated biological function.

Over a decade ago, the theoretical chemist Henry Schaefer declared: “It is clear

that theoretical chemistry has entered a new stage ... with the goal of being no

less than full partner with experiment”[1092].

Commenting on the two 1998 Chemistry Nobel Prize awardees in quantum

chemistry — Walter Kohn of the University of California, Santa Barbara, and

John Pople of Northwestern University — a reporter in The Economist wrote: “In

the real world, this could eventually mean that most chemical experiments are

8.1. The Merging of Theory and Experiment 239

conducted inside the silicon of chips instead of in the glassware of laboratories.

Turn off that Bunsen burner; it will not be wanted these ten years” (17 October

1998)!

It remains to be seen how effective “in silico biology” will be, but clearly a

new enthusiasm is stirring in the molecular biophysics community in the wake of

many methodological and technological improvements. The following categories

reﬂect improvements that lend computation a stronger basis than ever before:

1. Improvements in instrumentational and experimental techniques

[1043]. Rapid advances in sequencing and mapping genomes are being

made, as discussed in Chapter 1, making available an enormous amount

of biological data requiring analysis [83]. Many procedures in biomo-

lecular NMR and electron spectroscopy [361, 908, 1184], including 4D

NMR [1433] and X-ray crystallography [110, 994, 1224], are accelerating

the rate and improving both the accuracy and scope of structure determi-

nation; much of this progress was stimulated by the structural genomics

initiatives. And newer microscopic techniques such as scanning tunnel-

ing and cryo [61, 189, 336, 361, 685, 1077, 1286] are being applied. With

such advances, structures that were considered unconquerable a decade

ago are being resolved — RNAs, nucleosomes, ribosomes, ion channels,

and membrane proteins, for example — although limitations still remain

for macromolecular complexes. Theoreticians can use these structures

with other experimental data and biological information as solid bases for

simulations and computer analyses.

2. New models and algorithms for molecular simulations.Improvedforce

ﬁelds are being developed, some simpler (e.g., coarse-grained [1117])

and others more complex (e.g., polarizable, more variables [223]) that

are sophisticated versions of early coarse-grained (e.g., [749]) or po-

larizable (e.g., [1344]) protein folding models. Innovative models for

protein and DNA folding and dynamics and for macromolecular com-

plexes are shedding insights into important biological processes. Faster

and more advanced dynamic simulations of complex systems with full

account of long-range solvation and ionic effects are being used. Quantum-

mechanical and classical/quantum hybrid studies of biomolecules are

becoming routine. And many enhanced sampling methods are making pos-

sible simulation of a wide range of conformational states of biomolecules,

including computation of reaction rates [1116, 1117].

3. The increasing speed and availability of supercomputers, parallel

processors, and distributed computing. Faster, cheaper, and smaller com-

puting platforms and graphics workstations are entering the laboratory

at reduced costs, though computer memory requirements are explod-

ing. Supercomputing centers are making available very fast computing

platforms, and specialty hardware like Anton [1169] hold promise for

advancing macromolecular modeling and simulation.