Сборник докладов - Электроэнергетика глазами молодежи 2010
Подождите немного. Документ загружается.

180
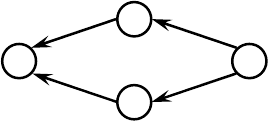
Рассмотрим граф на рисунке 3. Пусть веса всех дуг ε, а описанный выше
алгоритм дал
(вершина
– источник возмущения). Тогда при достижении
фронтом воздействия вершины ее надежность будет определена как
0
ε
.
Так, если учесть, что время распространения по дуге равно 1 ед., то к моменту
3 получим, что импульс дошел до
, а надежность
стала равна:
3
0
ε
0
ε
. (4)
Если учесть, что воздействие может носить длительный характер и
,
то при достижении фронта некоторого элемента его надежность может либо сразу стать
ниже критической надежности элемента
2
кр
, либо может стать ниже критиче-
ской после некоторого времени ∆
. Так, к моменту 3 надежность для
,
соот-
ветственно равна:
3
2
ε
1
ε
0
ε
;
3
2
ε
1
ε
0
ε
.
(5)
В случае, если веса дуг
,
ε, , то всегда будет существовать путь из
базовой вершины в контрбазовую, который будет вносить наибольший вклад в ухудшение
надежности. Для поиска такого «опасного пути» можно использовать любой известный
алгоритм нахождения кратчайшего пути. Например, для вершины
при 3 с учетом
весов дуг имеем ситуацию, показанную на рисунке 6.
Рисунок 6 – Поиск кратчайшего пути
Тогда на последнем шаге (3) алгоритма Флойда получаем матрицу расстояния
0 и матрицу последовательности узлов 0:
3
∞∞∞
0,8 ∞∞
0,4 ∞ ∞
0,7 0,2 0,3
; (6)
3
234
1 34
12 4
323
. (7)
Из матрицы 3 находим кратчайшее расстояние от
до
:
0,7. Из матрицы
3 видно, что путь из
в
проходит через вершину
(
3), тогда кратчайший путь:
. Кратчайший путь из
в
равен
. Полученный путь
соответствует базовому пути, который вносит наибольший вклад в ухудшение надежно-
сти узла
. Следовательно, во избежание дальнейшего ухудшения надежности узла
, в
момент времени 2 необходимо исключить данный путь из графа, что соответствует
отключению линии Л2.
3
3
3
3
0,2 0,8
0,4
0,3
181
Использование модели применительно к ПК RastrWin. Полученная модель мо-
жет быть применена в ПК RastrWin для ликвидации перегруза ветви по току. Для этого
каждой единице оборудования ПК RastrWin необходимо поставить в соответствие узел
графа возмущений. Дугой графа возмущений будет наличие электрической связи между
единицами оборудования, а направлением – направление перетока по соответствующей
ветви таблицы ПК RastrWin. В граф включается только то оборудование, на котором на-
блюдается нарушение по току. Узлы и дуги графа возмущений помещаются в отдельную
таблицу ПК RastrWin.
Алгоритм нахождения источников возмущений и поиска кратчайших путей от
контрбазовых вершин до базовых предполагается реализовать с помощью внутрипроцесс-
ного COM-сервера, стартующего при запуске ПК RastrWin и работающего прозрачно для
пользователя. Задачей COM-сервера является обработка событий от ПК RastrWin, а также
запуск COM-клиента, имеющего графический интерфейс. Такая реализация позволяет не
блокировать основной интерфейс ПК RastrWin, а также позволяет COM-серверу высту-
пать в роли посредника оперативной информации при создании динамической модели.
Динамическая модель позволит выполнять переключения на основе актуальных данных,
извлекаемых из ОИК СК2007. По окончании работы алгоритма должны быть найдены
наиболее опасные маршруты от всех источников возмущений к узлам, до которых дошло
возмущение. Далее на основе полученного списка маршрутов перебираются различные
комбинации переключений, из которых выбираются наиболее эффективные. В отчете
должен формироваться список возможных переключений для ликвидации нарушения на
данном этапе развития возмущения.
Заключение. В результате построения вероятностно-детерминистической модели
распространения возмущения на примере типовой схемы было показано, как распростра-
няется возмущение. На модели видно, как выходит из строя оборудование энергосети, не
получавшее импульса воздействия непосредственно. Показано, что внутренними источ-
никами возмущений могут являться контуры, обладающие эффектом положительной об-
ратной связи. Существенной особенностью модели является прямая зависимость надеж-
ности элемента от его положения в структуре, а также зависимость стойкости всей систе-
мы от выбранной при проектировании структуры. Предложен подход к использованию
модели в ПК RastrWin.
В дальнейшем для ПК RastrWin планируется разработка COM-сервера и COM-
клиента, осуществляющего поиск источников возмущений и изменяющего топологию се-
ти для ликвидации нарушения на основе предложенной модели.
Список использованных источников
1. Кощеев Л.А. Автоматическое противоаварийное управление в электроэнергетических
системах. Ленинград: Ленинградское отделение Энергоатомиздата, 1985. 143 с.
2. Кочкаров А.А., Малинецкий Г.Г. Распространение внешних воздействий по структуре
сложной системы//Математическое моделирование. 2006. №2 . С. 51–60.

182
МОДЕЛЬ ОЦЕНКИ ДЕФИЦИТА МОЩНОСТИ
ЭЛЕКТРОЭНЕРГЕТИЧЕСКОЙ СИСТЕМЫ
В.И. Зоркальцев, С.М. Пержабинский
ИСЭМ СО РАН
Введение. В Сибирском энергетическом институте (СЭИ, ныне ИСЭМ СО РАН),
разработана методика анализа надежности электроэнергетических систем (ЭЭС) [1–3], ба-
зирующаяся на методе многовариантных статистических испытаний (методе Монте-Карло).
Методика состоит из трех блоков:
1. Вероятностный блок, в котором формируются случайным образом возможные
состояния ЭЭС.
2. Блок оценки дефицита мощности сформированных расчетных состояний (модель
минимизации дефицита мощности).
3. Блок вычисления показателей надежности ЭЭС, в котором обрабатывается ин-
формация, накопленная в результате работы первых двух блоков (в том числе оценивают-
ся показатели вероятности и математического ожидания дефицита мощности в отдельных
узлах системы).
В данной методике блок расчета дефицита мощности занимает центральное место.
От его реализации зависит не только качество результатов, но и время проведения всего
цикла расчетов. Поэтому к модели минимизации дефицита мощности предъявляются осо-
бые требования. Она должна быть агрегированной, максимально адекватной действитель-
ности, легко реализуемой, рассчитываемой за максимально короткое время. Чем меньше
время оптимизации, тем большее количество случайных состояний можно «проиграть» и,
тем самым, увеличить точность оценки показателей.
Первые варианты модели оценки дефицита мощности ЭЭС, разработанные в СЭИ,
представлялись в виде задачи о максимальном потоке. Для их реализации применялся ал-
горитм Форда-Фалкерсона. При его использовании возникала неоднозначность распреде-
ления дефицита по узлам и, следовательно, неточность оценок вероятности и математиче-
ских ожиданий дефицита в
узлах системы. В связи с этим стала применяться двухэтапная
схема расчетов модели методом внутренних точек [4]. Сначала решалась задача миними-
зации дефицита мощности. Потом – задача равномерного распределения по узлам про-
порционально нагрузкам полученного минимального дефицита. В последующем была
предложена одноэтапная схема расчетов, использующая квадратичный критерий, обеспе-
чивающий одновременную минимизацию дефицита мощности с равномерным его распре-
делением по узлам [5].
Одним из направлений, повышающим адекватность модели оценки дефицита мощ-
ности, является учет потерь мощности при передаче ее по межузловым связям. В этой свя-
зи Г.Ф. Ковалевым была разработана модель, учитывающая потери мощности. В этой мо-
дели потери представляются в виде квадратичной функции от
передаваемой мощности по
линии электропередачи [5]. Поскольку в балансовых ограничениях-равенствах использу-
ются квадратичные функции, модель оценки дефицита мощности приобрела вид задачи
невыпуклого программирования. В данной статье приводится и теоретически обосновы-
вается способ сведения исходной модели к задаче выпуклого программирования, из реше-
ния которой по простым правилам можно получить решение исходной модели. Доказыва-
ется теорема о совпадении оптимальных решений исходной и модифицированной задачи
по основным показателям, представляющим интерес для анализа надежности, – по вели-
чинам дефицита мощности в отдельных узлах. Доказывается теорема о единственности
значения дефицита мощности в узлах для оптимальных решений.
183
Модель оценки дефицита мощности электроэнергетической системы с учетом
квадратичных потерь мощности в линиях электропередачи. Рассматривается схема
электроэнергетической системы, состоящая из узлов и некоторого набора связей между
ними. Заданы располагаемая мощность
, нагрузка
в -м узле ЭЭС, предел пропускной
способности
линии электропередачи, связывающей узлы и , 1, …, , 1, …, .
Считается, что для всех и ,
0,
0,
0. Если
0 при некоторых и , то
это означает, что фактически поток мощности из узла в узел невозможен.
Переменными задачи являются:
– используемая мощность,
– покрываемая на-
грузка в узле ,
– поток мощности из узла в узел .
Требуется минимизировать суммарный дефицит мощности в системе
min, (1)
учитывая балансы мощности в узлах
1α
0, 1, …, , (2)
и линейные двусторонние ограничения-неравенства на переменные
0
, 1, …, , (3)
0
, 1, …, , (4)
0
, 1, …, , 1, …, . (5)
Замечание 1. Коэффициенты α
, используемые для описания потерь при передаче
электроэнергии из узла в узел , заданы и удовлетворяют условию: 2α
1, для всех
и . Это условие означает то, что дополнительная единица мощности, передаваемая из
узла в узел , достигает узла с положительным значением.
Определение 1. Тройку векторов , , , удовлетворяющих балансовым уравнени-
ям (2) и неравенствам (3)–(5), будем называть допустимым решением задачи (1)–(5).
Множество таких троек векторов образует
множество допустимых решений.
Множество допустимых решений задачи (1)–(5), как правило, невыпукло (за ис-
ключением некоторых вырожденных случаев). Действительно, пусть существуют такие
допустимые решения
, , ̃
,
, , ̂
, что ̃̂, тогда их выпуклая комбинация
λ
1 λ
, λ
1 λ
,
λ̃
1 λ
̂
не удовлетворяет балансовым ограничени-
ям (2). Значения функций в левой части ограничений (2) равны λ
1 λ
∑
α
̃
̂
.
Эти величины будут положительны для λ
0, 1
и всех таких, что существует номер ,
при котором ̃
̂
.
Представление модели оценки дефицита мощности в виде задачи выпуклого
программирования. Для представления задачи (1)–(5) в виде эквивалентной задачи вы-
пуклого программирования заменим ограничения (2) на следующие:
1α
0, 1, …, . (6)
Множество векторов, соответствующих ограничениям (3)–(6), является выпуклым, для
любой выпуклой комбинации двух допустимых решений
, , ̃
,
, , ̂
выполняются
ограничения (3)–(6).
184
Задачу (1)–(5) будем называть исходной задачей минимизации дефицита мощно-
сти. Задачу (1), (3)–(6) будем называть расширенной задачей минимизации дефицита
мощности. Множество допустимых решений расширенной задачи содержит множество
решений для исходной задачи минимизации дефицита мощности. Покажем, что распреде-
ление дефицита мощности по узлам системы, найденное в результате решения задачи (1),
(3)–(6), будет оптимальным и в задаче (1)–(5).
Теорема 1. Пусть значения переменных
,
, ̃
1, …, , 1, …, являются
оптимальным решением задачи (1), (3)–(6), тогда существуют такие
, ̂
, что значе-
ния переменных
,
, ̂
, 1, …, , 1, …, составляют оптимальное решение за-
дачи (1)–(5).
Доказательство. Пусть векторы
,
, ̃
1, …, , 1, …, являются опти-
мальным решением задачи (1), (3)–(6). Определим неотрицательные величины невязок ог-
раничений (2)
∆
1α
̃
̃
̃
, 1, …, . (7)
Зафиксируем найденное значение и рассмотрим следующую задачу:
∆
min, (8)
при условиях
1α
∆
, 1, …, . (9)
∆
0, 1, …, , (10)
0
, 1, …, , (11)
0
, 1, …, , 1, …, . (12)
Покажем, что для оптимального решения задачи (8)–(12) выполняется равенство
∆
0, 1, …, .
Приведем алгоритм решения задачи (8)–(12). В качестве начальных значений ∆
,
,
используем векторы ∆
, , ̃ которые вместе с вектором удовлетворяют ограниче-
ниям задачи (8)–(12). Отметим, что невязка балансового ограничения имеет место или
вследствие избыточной генерации в узле , или (и) вследствие передачи в этот узел из дру-
гих узлов дополнительной мощности.
На итерации 1, 2, …, будем рассматривать последовательно
все узлы .
Если ∆
0, то полагаем
,
, 1, …, .
Если ∆
0, то:
1) при
,
а) если
∆
, положим
∆
,
, 1, …, ;
б) если
∆
, полагаем
и вводим величины
такие, что
0
, 1, …, , (13)
и при этом
185
1 α
1α
∆
.
2) при
, полагаем
, величины
должны удовлетворять условию (13) и
за счет их последовательного сокращения добиваемся выполнения равенства
1 α
1α
∆
.
Отметим, что после указанных преобразований для данного номера имеет место
равенство:
1α
0. (14)
Причем для всех выполняется (13) и неравенства
0
. (15)
После уменьшения генерации по всем узлам и назначения меньших объемов по-
ступающей в узлы мощности, невязки балансовых ограничений (2) на итерации 1, вы-
числяемые по правилу (7) при
, ̃
, будут определяться соотношением
∆
, 1, …,
. (16)
Из (13)–(16) следует, что для
, ∆
,
,
, 1, …, , 1, …, будут
выполняться условия (9)–(11).
Поскольку согласно (13) на всех итерациях
0, то
̂
при ∞
для некоторого ̂
, 1, …, , 1, …, . Следовательно, ̂
̂
0 при ∞.
Из (16) следует, что ∆
0 при ∞ для всех 1, …, . В силу (15)
при ∞
для некоторого 0. Причем векторы , ̂, , ∆
0 удовлетворяют условиям (9)–(12), по-
скольку (9)–(12) выполняются на всех итерациях для
,
, , ∆
. Теорема доказана.
Из теоремы 1 и указанных выше соотношений множества допустимых решений ис-
ходной и расширенной задачи минимизации дефицита мощности следует справедливость
обратного утверждения: если значения переменных
,
, ̃
, 1, …, , 1, …, со-
ставляют оптимальное решение исходной задачи минимизации дефицита мощнос-
ти (1)–(5), то они составляют и оптимальное решение расширенной задачи минимизации
дефицита мощности (1), (3)–(6).
Доказанная теорема означает также, что оптимальные решения расширенной и ис-
ходной задачи минимизации дефицита мощности совпадают по особо интересующим в
этой модели переменным – по покрываемым
нагрузкам
и соответственно по величинам
дефицита мощности
во всех узлах 1, …, .
Отметим, что решая задачу (8)–(12), можно перейти от оптимального решения
расширенной задачи к оптимальному решению исходной задачи минимизации дефицита
мощности и по остальным переменным.
Задача (1), (3)–(6) имеет решение, так как множество допустимых решений не пус-
то (значения 0, 0, 0 составляют допустимое решение), выпукло и ограничено
(в силу условий (3)–(5)), целевая функция линейна. Из существования решения в задаче
186
(1), (3)–(6) следует (согласно Теореме 1) существование решения в задаче (1)–(5). Дока-
жем, что решение в задаче (1), (3)–(6) единственно по переменным, составляющим компо-
ненты вектора . Это важное свойство обеспечивает единственность распределения ми-
нимального суммарного дефицита по узлам системы в рассматриваемой здесь модели.
Теорема 2. Решение задачи (1), (3)–(6) единственно по переменным
, 1, …, .
Доказательство. Предположим, что у задачи (1), (3)–(6) существует два оптималь-
ных решения
, , ̃
и
, , ̂
такие, что
. (17)
Оба решения, поскольку они оптимальные, имеют одно и то же значение целевой функции
. (18)
Для задачи выпуклого программирования множество оптимальных решений вы-
пукло, следовательно, оптимальным решением должен быть и набор векторов
,
,
таких, что
0,5
,
0,5
,
0,5
̃̂
. (19)
В силу (17) для некоторого
1, …,
значения переменных
и
будут раз-
личаться. Следовательно, одна из этих величин будет меньше другой. Пусть для опреде-
ленности
. (20)
То есть для решения
, , ̃
узел с номером будет дефицитным. Вследствие этого
, ̃
0 для всех
1, …,
. (21)
Действительно, если
, то можно сократить дефицит в узле , а значит, и
суммарный дефицит, увеличивая значение
.
Если для некоторого ̃
0, то передаваемая мощность из узла в узел дохо-
дит в объеме меньшем, чем ̃
, на величину потерь. Поэтому такой поток способствует
меньшему сокращению суммарного дефицита по всем узлам. Если этот поток уменьшить
на единицу, то это приведет к сокращению на единицу дефицита в данном узле и возмож-
ному увеличению, меньшему, чем на единицу, дефицита в других узлах. Следовательно,
суммарный дефицит сократится. Итак, для оптимального
решения из дефицитного узла не
может быть потоков мощности. Свойства (21) доказаны.
Представим в виде функции выражение в левой части условия (6) для узла
, ,
1 α
. (22)
В силу дефицитности для узла решения
, , ̃
условие (6) должно выполняться
в виде равенства
, , ̃
0, (23)
иначе, если бы значение при таких аргументах было бы положительным, величину
можно было бы увеличить, не нарушая условие (6). Тем самым сократив дефицит в узле ,
сократим и суммарный дефицит, что противоречит оптимальности решения
, , ̃
.
Из (21)–(23) следует, что
̃
α
̃
. (24)
187
Согласно условию (6)
, , ̂
0. (25)
Отсюда, учитывая, что
, .̃
0 для всех 1, …, , имеем
̂
α
̂
. (26)
Предположим, что ̃
̂
для всех 1, …, . Тогда из (24), (26) будет следо-
вать, что
. Это противоречит (20). Предположение не верно. Для некоторого
̃
̂
. (27)
Множество таких номеров обозначим как . Отметим, что
0,5̃
0,5̂
0,25̃
̂
0,25̃
̂
. (28)
Из определения функции , условия (19) и равенства (28) следует, что
,
,
0,5
, , ̃
0,5
, , ̂
0,25α
̃
̂
.
Из (27) и условия следует, что третья составляющая положительна. Отсюда
,
,
0. (29)
Из (19), (20) следует, что
. Это означает, что оптимальное реше-
ние
,
,
будет давать дефицит
в узле . Вместе с тем, неравенство (29)
означает, что значение переменной
можно увеличить, не нарушая условия (6). Тем са-
мым будет сокращаться дефицит в узле и суммарный дефицит. Это противоречит тому,
что решение
,
,
является оптимальным. Полученное противоречие доказывает
ошибочность исходного предположения о существовании двух оптимальных решений,
удовлетворяющих условию (17). Теорема доказана.
Заключение. Сформулируем основные результаты.
1. Для модели оценки дефицита мощности ЭЭС с квадратичными потерями мощ-
ности в линиях электропередачи предложен и теоретически обоснован способ представ-
ления её в виде задачи выпуклого программирования путем
замены балансовых ограниче-
ний-равенств на ограничения-неравенства.
2. Доказано, что дефицит мощности в данной модели однозначно распределяется
по узлам электроэнергетической системы. Это гарантирует однозначность оценок вероят-
ности и математических ожиданий дефицита в узлах системы после проведения всего
цикла расчетов.
Список использованных источников
1. Руденко Ю.Н., Чельцов М.Б. Надежность и резервирование в электроэнергетических системах. Новоси-
бирск: Наука, 1974. 263 с.
2. Ковалев Г.Ф., Лебедева Л.М. Комплекс моделей оптимизации режимов расчетных состояний при оценке
надежности электроэнергетических систем / Препринт. Иркутск: ИСЭМ СО РАН, 2000, с. 32–39.
3. Ковалев Г.Ф., Лебедева Л.М. Модель оценки надежности
электроэнергетических систем при долгосроч-
ном планировании их работы // Электричество. 2000. № 11. c.17–24.
4. Дикин И.И., Зоркальцев В.И. Итеративное решение задач математического программирования: алгорит-
мы метода внутренних точек. Новосибирск: Наука. Сиб. отд-ние, 1980. 144 с.
5. Зоркальцев В.И., Ковалев Г.Ф., Лебедева Л.М. Модели оценки дефицита мощности электроэнергетиче-
ских систем./
Препринт. Иркутск: ИСЭМ СО РАН, 2000, с.17–22.
6. Зоркальцев В.И., Лебедева Л.М., Пержабинский С.М. Модель оценки дефицита мощности электроэнер-
гетической системы с учетом квадратичных потерь мощности в линиях электропередач // Сибирский
журнал вычислительной математики / РАН. Сиб. отд-ние.– Новосибирск, 2010. Т.13, №3. С. 285–295.
188
МОДЕЛЬ РАСЧЕТА УСТАНОВИВШЕГОСЯ РЕЖИМА
БОЛЬШОЙ ЭЛЕКТРОЭНЕРГЕТИЧЕСКОЙ СИСТЕМЫ
С ПРИМЕНЕНИЕМ ДИАКОПТИКИ НА ОСНОВЕ
КОЭФФИЦИЕНТОВ РАСПРЕДЕЛЕНИЯ
И ЭЛЕМЕНТОВ НЕЙРОННЫХ СЕТЕЙ
В.С. Павлюков, С.В. Павлюков
ЮУрГУ
В настоящее время управление режимами работы крупных электроэнергетических
систем (объединений) требует развития аналитических и других математических моделей,
которые должны базироваться на совершенствовании расчета и анализа различных режи-
мов, в том числе и установившихся. В качестве одного из подходов предлагается приме-
нение элементов диакоптики (разделение, рассечение), позволяющих повысить эффектив-
ность решения данной задачи за счет совмещенных по времени расчетов в отдельных под-
системах, особенно при развитии мультипрограммных комплексов или технологий парал-
лельных вычислительных систем в АСДУ энергосистем.
Моделирование расчета установившихся режимов электрических систем осущест-
вим с помощью коэффициентов распределения, на базе которых можно разрабатывать как
безытеративные, так и итерационные методы, гарантирующих решение задачи при раз-
личных комбинациях исходных, физически существующих, режимных параметров.
Большую сложную электрическую систему с помощью рассечения через заданное
множество узлов (или линий связи [1]) предлагается разделить на несколько подсистем
(допустим, регионального уровня), для каждой из которых далее автономно производятся
детальные расчеты и анализ характерных установившихся режимов, осуществляется экви-
валентирование одной части системы относительно других [2] и прочее. Таким подходам
будут соответствовать разнообразные модели описания задач определения потоков и по-
терь мощности, энергии.
При разделении схемы замещения большого объема электрической системы на
подсистем (для иллюстрации изложения зададим 2), математические модели для век-
торов-столбцов токов ветвей дерева
(верхний индекс обозначает номер подсистемы)
при задании режимных параметров в виде векторов-столбцов узловых токов
(нижний
индекс обозначает внутренние задающие токи узлов подсистем) запишутся в матричной
форме
I
I,I
I,II
I
I,II
∆
I,II
, (1)
II
II,I
II,II
II,I
∆
I,II
II
, (2)
где
I
– вектор-столбец внутренних задающих токов узлов первой подсистемы;
II
– век-
тор-столбец внутренних задающих токов узлов второй подсистемы;
I,II
,
II,I
– векторы-
столбцы задающих узловых токов во множестве граничных узлов подсистем; ∆
I,II
– век-
тор-столбец множества задающих граничных токов, перетекающих через граничные узлы
из подсистемы I в подсистему II при их объединении;
,
,
,
– подблоки соответст-
венно матриц собственных ( = I или II) и взаимных ( = I, II при ) коэффициентов
распределения для деревьев подсистем разделенной схемы электрической системы.
189
Для сохранения режима исходной и разделенной схем электрической системы не-
обходимо на границе между подсистемами соблюдать следующее условие
∆
I,II
II
∆
II,I
I
, (3)
для которого, на основании закона Ома с использованием токов ветвей деревьев подсис-
тем, получаем
∆
I,II
II
I,II
I
I
, (4)
∆
II,I
I
II,I
II
II
, (5)
где
I,II
,
II,I
– подблоки матриц коэффициентов распределения граничных узлов, соот-
ветствующие разомкнутым схемам подсистем-деревьев;
I
,
II
– диагональные матри-
цы полных сопротивлений ветвей деревьев подсистем;
I
,
II
– векторы-столбцы токов
ветвей деревьев подсистем (при отсутствии э.д.с. в ветвях); – операция транспонирования.
Совокупность уравнений (3)–(5) моделирует между подсистемами структуру связи,
которая представляется вектором-столбцом граничных задающих токов
∆
I,II
∆
I,II
I
I,I
I
I,II
I,II
II,I
II
II,II
II
II,I
II,I
,
(6)
где ∆
I,II
I
I,II
II,I
II
II,I
;
– диагональная матрица сопротивлений вет-
вей дерева ( принимает значения I или II).
Векторы-столбцы напряжений узлов подсистем моделируются зависимостями
∆
I
I
I
I
, (7)
∆
II
II
II
II
, (8)
где
– напряжение балансирующего узла между смежными подсистемами; – единич-
ная диагональная матрица.
Матричные уравнения (1)–(8) представляют математическую модель, позволяю-
щую выполнять расчеты установившихся режимов больших электроэнергетических сис-
тем по иерархическому способу. В силу нелинейности модели итерационное решение
можно организовать, используя простой метод, к примеру, Зейделя, или более сложный,
но с быстрой сходимостью в окрестности решения, как, например, методы Ньютона.
Режимные параметры узлов электрических систем могут иметь разную форму
представления. Самая распространенная – детерминированная. В современных условиях
технико-экономических отношений между производителями, транспортировщиками и по-
требителями электроэнергии расчеты электроэнергетических задач требуют исходных ре-
жимных параметров, обеспеченных более полной и достоверной информацией. В данной
работе режимную узловую информацию высоковольтной или питающей системы модели-
руют в виде вектора-функции графиков полных мощностей
. (9)
Зависимости компонент узловых нагрузок рассматриваются в виде произведений
средних значений активных
и реактивных
мощностей и соответствующих функций
,
, средние значения каждой из которых за период времени равны единице,
,
. (10)
