Сборник докладов - Электроэнергетика глазами молодежи 2010
Подождите немного. Документ загружается.


210
Задача определения ПСЗ различных элементов энергосистем, в том числе ЛЭП, ак-
туальна, поскольку погрешности параметров схемы замещения при использовании спра-
вочных и пр. данных весьма велики [7] (см. таблицу 1). Знание более точных параметров
линий увеличит точность любых расчетов, где используются эти параметры. Следует от-
метить, что коррекцию ПСЗ ЛЭП, связанную с изменениями погодных условий и элек-
трической нагрузки, достаточно выполнять лишь несколько раз в сутки.
Таблица 1 – Погрешности параметров схемы замещения
Параметр
Причины возникновения
погрешности
Диапазон
погрешности
Влияние режима
на погрешность
Неучёт поверхностного эффекта, влияния
погодных условий
–24…+8% сильное
Неточность задания эквивалентных гео-
метрических параметров. Многократно
заземленные тросы и параллельные цепи
–10…+8% слабое
Неучёт изменения стрелы провеса, нали-
чия заземленного троса, параллельных
цепей, проводимости грунта и влажности
воздуха
25…30% сильное
Конструктивные, режимные и метеоро-
логические условия
в 1,5 – 3 раза очень сильное
Предполагая, что используются исключительно современные цифровые техноло-
гии регистрации, получения и передачи информации, основанные на одномоментных вы-
сокоточных измерениях [8], было выполнено исследование обсуждаемых методов.
При исследовании первой модели, основанной на данных двух различных по мощ-
ности режимов, подтвердилось, как и было получено ранее, что активную проводимость
оценить не представляется возможным. Её размерность по сравнению с другими парамет-
рами настолько мала, что практически любая погрешность в исходных данных при расче-
те приводит к существенному отклонению расчётного значения (поэтому далее этот па-
раметр не рассматриваем).
Исследование велось по представленным выше формулам с внесением погрешно-
стей в параметры
,
,
, δ
первого режима, а также изменением мощностей начала
линии двух режимов
,
. На основании проведенных опытов были установлены зави-
симости погрешностей ПСЗ (∆, ∆, ∆) от различных факторов.
По результатам исследования первой модели можно сделать выводы:
1) определить с требуемой точностью активную проводимость линии весьма
сложно, что связано с ее малой величиной и большой чувствительностью к погрешностям
исходных данных;
2) современные измерительные комплексы (совокупность трансформаторов тока,
трансформаторов напряжения, регистраторов), используемые в наших энергосистемах и
обеспечивающие точность измерений не выше 0,5–1%, позволяют в ходе решения обрат-
ной задачи расчёта найти достаточно точно лишь индуктивное сопротивление и индук-
тивную проводимость линии;
3) можно предположить, что существует связь погрешности определения ПСЗ при
решении обратной задачи с соотношениями активных мощностей в первом и втором ре-
жимах, причём чем больше разность активных мощностей в этих двух режимах, тем
211
меньше погрешность. Однако зависимость изменения расчётных значений ПСЗ от пара-
метров режимов (по мощности), используемых в качестве исходных данных, неоднознач-
на: в некоторых случаях с ростом активной мощности увеличиваются и погрешности, для
других случаев – наоборот.
Также следует учитывать, что с ростом активной мощности постепенно увеличива-
ется и активное сопротивление, поэтому находить ПСЗ по двум режимам с большой раз-
ницей в активных мощностях является некорректным.
4) поскольку при решении обратной задачи установлена зависимость погрешности
расчёта ПСЗ от режимов по активной мощности, то можно предположить, что существуют
похожие зависимости и от режимов реактивной мощности.
Таким образом, получаем, что в рассматриваемом случае, как и в выполненных ра-
нее исследованиях, вопросы выбора режимов для решения задачи требуют отдельного
изучения.
Использование зарубежных измерительных устройств существенно улучшает ре-
зультаты определения ПСЗ. Причём с точки зрения оценивания погрешностей ПСЗ режи-
мы, рассмотренные в данном случае, были «тяжелее» режимов, рассмотренных для отече-
ственных измерительных устройств (два рассматриваемых режима очень близки по зна-
чениям передаваемой мощности). При этом погрешности определения ПСЗ оказываются
ниже. Однако основным недостатком рассмотренной модели при решении обратной зада-
чи является потребность в параметрах двух режимов, причем установлено влияние соот-
ношений мощностей этих режимов на погрешности определения ПСЗ.
Вторая модель основана на параметрах, получаемых только из одного режима, и
лишена недостатков, присущих первой модели. Исследование в данном случае проводи-
лось при варьировании погрешностей, вносимых в параметры
, δ
,
,
δ
,
, γ
,
, γ
в различных комбинациях.
Полученные результаты показали, что погрешности, вносимые эксплуатируемыми
отечественными измерительными преобразователями, не позволяют достаточно точно оп-
ределять активное сопротивление и проводимость линии. Кроме того, реактивное сопро-
тивление и проводимость определяются с погрешностью, сопоставимой с погрешностью,
получаемой при использовании справочных данных. Использование более точных совре-
менных зарубежных измерительных преобразователей существенно улучшаете результат
и может быть рекомендовано к применению для решения поставленной задачи. Получен-
ные данные говорят о том, что погрешность определения активного сопротивления ∆ не
будет превышать 15%, для реактивного сопротивления ∆ и проводимости ∆ она соста-
вит не более 5%, активной проводимости ∆ – 20%. Вероятность появления максималь-
ной погрешности одновременно в
каждом из используемых параметров
, δ
,
, δ
,
, γ
,
, γ
чрезвычайно мала. Если предположить возмож-
ность однократной ошибки, то погрешности определения , , и будут существенно
меньше.
Если учесть, что с увеличением ошибок в параметрах уменьшается вероятность их
появления (как уже упоминалось, вероятность появления ошибок в каждом из параметров
чрезвычайно мала), то можно предложить некоторый «фильтр ошибок».
При достаточном
количестве проведенных измерений распределение ошибок относительно эталонных (дей-
ствительных) значений будет равномерно, усреднение полученных данных позволит най-
ти действительные значения ПСЗ. Это вполне возможно осуществить, т.к. использование
рассмотренной выше технологии позволяет проводить измерение параметров с высокой
частотой на небольшом временном интервале, на котором погодные условия и режимы
нагрузки
можно считать неизменными.
212
Заключение. Проведенные исследования задачи определения параметров схемы
замещения показывают возможность использования для её решения средств векторной
регистрации параметров электрического режима. Современные измерительные преобра-
зователи совместно с PMU обеспечивают точность измерения токов и напряжений и рас-
чётных параметров электрического режима узла, достаточную для вычисления текущих
параметров схемы замещения элемента сети. В работе это показано на примере
П-образной схемы замещения линии электропередачи. Возможность применения отечест-
венных устройств для этих целей требует дополнительных исследований.
Список использованных источников
1. Ming Zhou, Virgilio A. Centeno, James S. Thorp and Arun G. Phadke. An Alternative for In-
cluding Phasor Measurements in State Estimators. IEEE Trans. on Power Systems, Vol. 21,
No. 4, November 2006.
2. Optical Solutions for AC. Alstom Grid, 2010. URL: http://www.nxtphase.com.
3. Гуртовцев А.Л. Оптические трансформаторы и преобразователи тока // Новости элек-
тротехники. 2009. №5(59). URL: http://www.news.elteh.ru/arh/2009/59/05.php.
4. Бердин А.С., Крючков П.А. Формирование параметров модели ЭЭС для управления
электрическими режимами. Екатеринбург: УГТУ, 2000. 107 с.
5. Методы определения параметров схемы замещения для задач управления электриче-
скими режимами / А.С.Бердин, П.А.Крючков, А.А.Суворов, С.Н.Шелюг // Проблемы
развития и функционирования электроэнергетических систем: Сб. тр.. Екатеринбург:
УГТУ, 2000. С.25-31.
6. Адаптивные методы определения параметров схемы замещения линий электропередачи
/ А.С.Бердин, П.А.Крючков, А.А.Суворов, С.Н.Шелюг // Передача энергии переменным
током на дальние и сверхдальние расстояния: тр. межд. науч.-техн. конф. (15-19 сен-
тября 2003, Новосибирск, Россия). Новосибирск: СИБНИИЭ, 2003. Т.2. С.91-9.
7. Идельчик В.И., Новиков А.С., Паламарчук С.И. Ошибки задания параметров схем за-
мещения при расчетах режимов электрических систем // В сб. «Статистическая обра-
ботка оперативной информации в электроэнергетических системах». Иркутск, 1979.
С.145-152.
8. Особенности и перспективы развития WAMS в России. ООО «АльтероПауэр», 2009.
URL: http://www.alteropower.ru/publications/25/.

213
ОПРЕДЕЛЕНИЕ ПРЕДЕЛЬНЫХ ПО СТАТИЧЕСКОЙ
УСТОЙЧИВОСТИ И ДОПУСТИМОСТИ ПАРАМЕТРОВ РЕЖИМОВ
НЕРЕГУЛИРУЕМОЙ ЭЛЕКТРОЭНЕРГЕТИЧЕСКОЙ СИСТЕМЫ
НА ОСНОВЕ АКТУАЛЬНОЙ МАТРИЦЫ СОБСТВЕННЫХ
И ВЗАИМНЫХ ПРОВОДИМОСТЕЙ ЭДС
ЭКВИВАЛЕНТНЫХ ГЕНЕРАТОРОВ
М.А. Соболева М. А., А.Г. Фишов
НГТУ
Введение. Электроэнергетические системы (ЭЭС) характеризуются распределенно-
стью элементов на большой территории, скоротечностью протекания процессов при воз-
действиях внешних и внутренних возмущений, зависимостью от случайных факторов, од-
нако при этом к ним предъявляются высокие требования по качеству, надежности, безо-
пасности и экономичности электроснабжения потребителей [1].
К числу основных требований по надежности ЭЭС
относятся требования по устой-
чивости режима. Различают статическую и динамическую устойчивость режима. Статиче-
ская устойчивость рассматривается при малых возмущающих воздействиях и колебаниях
режимных параметров ЭЭС, динамическая – при больших возмущениях и отклонениях
параметров режима. Расчеты устойчивости выполняются при проектировании и эксплуа-
тации ЭЭС для выбора основной схемы, определения допустимых режимов и мероприя-
тий по повышению устойчивости, а так же для определения настройки систем режимного
и противоаварийного управления [3].
Современная технология расчетов статической устойчивости режимов ЭЭС. В
строгой постановке решение задачи проверки статической устойчивости предполагает со-
ставление системы дифференциальных уравнений движения роторов электрических ма-
шин, объединенных алгебраическими уравнениями балансов токов и напряжений в узлах
электрической сети. После линеаризации этой системы уравнений в точке положения рав-
новесия возможно получение характеристического уравнения. Система статически устой-
чива, если действительные корни и действительные части комплексных корней характери-
стического уравнения отрицательны. Наличие комплексных корней с положительной дей-
ствительной частью соответствует появлению самораскачивания. При положительных дей-
ствительных корнях нарушение статической устойчивости
носит апериодический характер.
При эксплуатации сложных ЭЭС применение анализа корней характеристического
уравнения весьма затруднительно, поскольку требует учета полной размерности задачи и
значительного времени для расчетов. Контроля статической апериодической устойчиво-
сти для правильно спроектированной энергосистемы и настроенных систем регулирова-
ния, как правило, оказывается вполне достаточно, поэтому проводится анализ только ста-
тической
апериодической устойчивости методом утяжеления (по смене знака свободного
члена характеристического уравнения при утяжелении заведомо устойчивого установив-
шегося режима). Если выбором формы записи уравнений установившегося режима, зави-
симых и независимых переменных добиться совпадения характеристической матрицы,
используемой при анализе статической устойчивости, и матрицы Якоби, используемой
при решении уравнений установившегося режима методом Ньютона, их определители бу-
дут равны. Таким образом, по смене знака определителя матрицы Якоби и расхождению
итерационного процесса решения уравнений установившегося режима можно судить о на-
рушении статической апериодической устойчивости при утяжелении режима ЭЭС [1, 2].
На практике предельные режимы энергосистем определяются не только условиями
устойчивости режима, но и допустимостью загрузки оборудования, уровнем напряжения в
214
электрической сети. Для их учета используется подробная цифровая модель режима ЭЭС,
учитывающая актуальную топологию и параметры электрической сети, ограничения по
загрузке оборудования. Достоинства и недостатки данной технологии проявляются по-
разному в различных задачах управления режимами ЭЭС. Наиболее адекватна она для за-
дач проектирования, заблаговременного определения системных ограничений и настроек
противоаварийной автоматики (в режимах ДО). В задачах управления реального времени
недостатки данной технологии проявляются особенно остро, т.к. она нуждается в боль-
шом объеме актуальных режимных данных и требует больших вычислительных затрат.
Технология расчетов статической устойчивости режимов ЭЭС на основе акту-
альной матрицы собственных и взаимных проводимостей ЭДС эквивалентных генерато-
ров ЭЭС, определяемой по данным СМПР. Внедрение в ЭЭС технологии распределенных
векторных измерений в основе системы мониторинга переходных режимов (СМПР) по-
зволяет реализовать качественно новый подход при решении задач управления режимами
энергосистем. СМПР предполагает установку регистраторов параметров переходных ре-
жимов на объектах энергосистемы с последующей передачей данных в центры диспетчер-
ского управления. Особенность технологии – синхронизация измерений и, как следствие,
фазовая привязка контролируемых параметров (частоты, токов, напряжений, активных и
реактивных мощностей, фазовых углов) [4]. Такие параметры обладают высокой инфор-
мативностью. Так, может быть идентифицирована актуальная комплексная матрица соб-
ственных и взаимных проводимостей (СВП) ЭДС эквивалентных генераторов, опреде-
ляющая угловые характеристики мощности генераторов:
·
·sinα
·
·
·sinα
δ
…
·
·sinα
·
·
,
·sinα
δ
·
·cosα
·
·
·cosα
δ
…
·
·cosα
·
·
,
·cos α
δ
1
где матрица СВП
…
…
…
…
, (2)
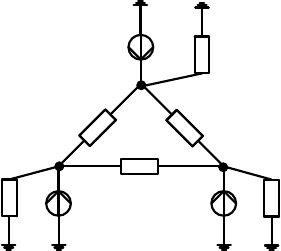
а замещение режима генераторов ЭЭС производится расчетной схемой (рисунок 1).
E1
Y11
E2
Y22
En
Ynn
Y1n
Y2n
Y12
Рисунок 1 – Расчетная схема замещения режима генераторов ЭЭС
на основе актуальной матрицы СВП ЭДС эквивалентных генераторов
215
Расчет предельных по условиям статической устойчивости режимов энергосис-
темы на основе актуальной матрицы СВП ЭДС эквивалентных генераторов. Прежде чем
говорить о расчете предельных по статической устойчивости режимов ЭЭС следует про-
анализировать возможности и особенности использования данной модели учета ограни-
чений по статической устойчивости параллельной работы генераторов. В своем исходном
виде модель не содержит других узлов привычной схемы замещения ЭЭС кроме узлов
ЭДС генераторов. По сути, это означает, что нагрузки системы представлены линейными
шунтами, а учет или не учет регулирования напряжения зависит от выбора схемы заме-
щения генератора и определения условий изменения соответствующих ЭДС.
Имея в виду то обстоятельство, что речь идет о контроле устойчивости по данной
модели в темпе процесса и использовании его результатов в системе противоаварийной
автоматики имеет смысл выделить два этапа управления:
управление, обеспечивающее устойчивость непродолжительного квазиустано-
вившегося режима, возникающего непосредственно после затухания электроме-
ханического переходного процесса;
управление, обеспечивающее устойчивость собственно послеаварийного режима.
На первом этапе можно не учитывать основные ограничения по допустимости ре-
жимных параметров в силу его непродолжительности, а также работу инерционных сис-
тем регулирования. Основной задачей управления является сохранение устойчивости па-
раллельной работы электростанций и, в этом случае, можно получать оценки ограничений
по статической устойчивости при допущении о постоянстве переходной ЭДС эквивалент-
ных генераторов за переходным сопротивлением.
На втором этапе управления продолжительность режима существенна и ограниче-
ния по допустимой загрузке оборудования и отклонениям напряжений должны учиты-
ваться в полном объеме. Задачей управления в этом случае является как сохранение ус-
тойчивости режима, так и обеспечение его допустимости. Существующая технология оп-
ределения предельных режимов по условиям допустимости послеаварийных режимов ре-
шает именно эту задачу и, разрабатывая технологию мониторинга запасов устойчивости и
допустимости режимов ЭЭС на основе матрицы СВП, необходимо обеспечить ее решение
в полном объеме.
Результаты расчетов предельных мощностей эквивалентных генераторов для
квазиустановившегося послеаварийного режима (по модели «нерегулируемой» ЭЭС) и их
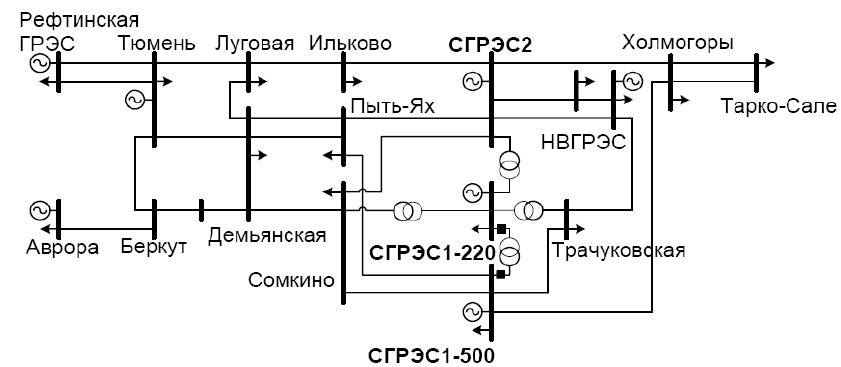
сопоставление. Сопоставительные расчеты проведем для Сургутского энергоузла, полная
схема которого приведена на рисунке 2, а эквивалентная (на основе актуальной матрицы
СВП ЭДС эквивалентных генераторов) – на рисунке 3.
Рисунок 2 – Полная схема Сургутского энергоузла
216
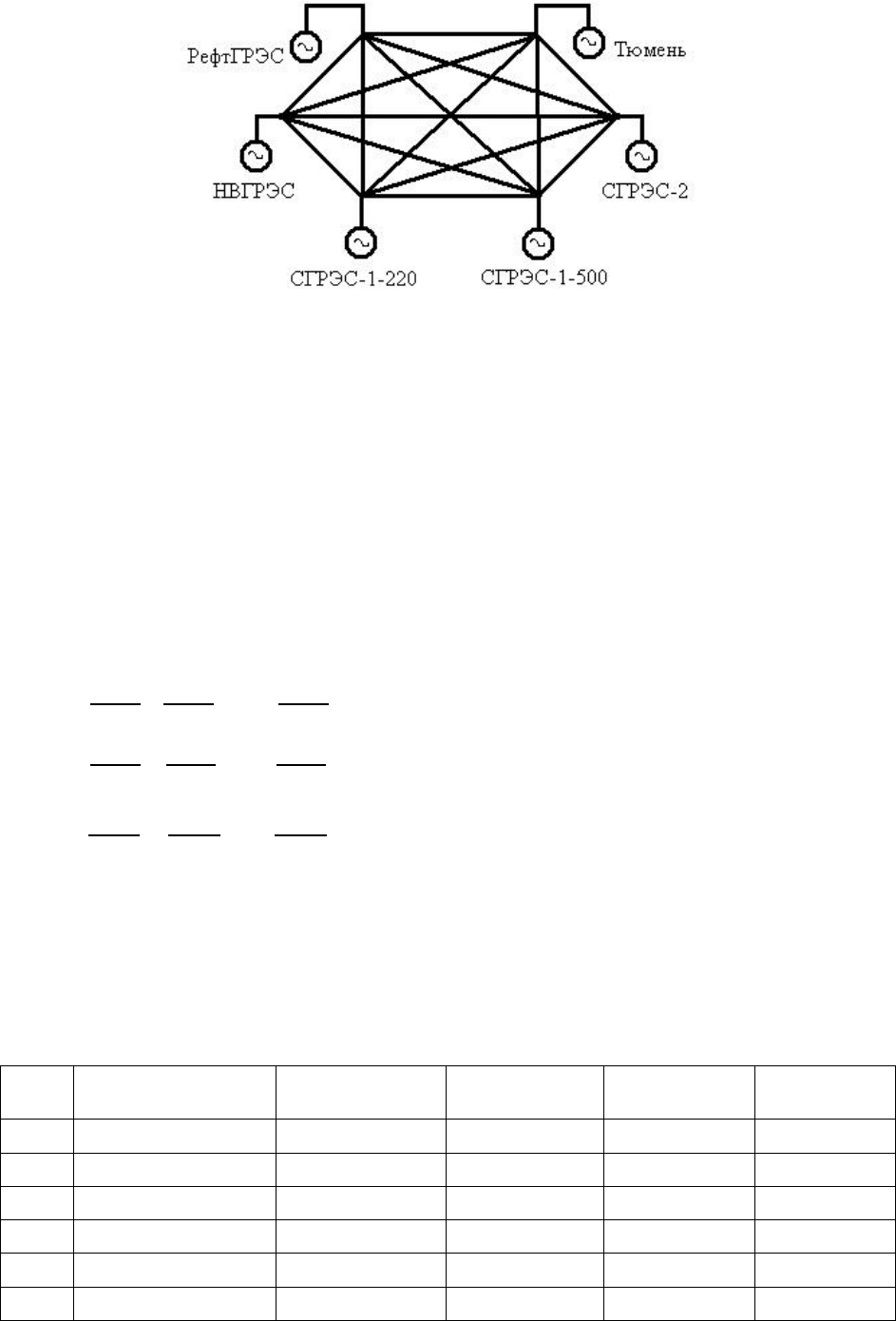
Рисунок 3 – Эквивалентная схема Сургутского энергоузла
Модель установившегося режима эквивалентных генераторов представим в виде
балансов их активных мощностей в узлах ЭДС:
·
·sinα
·
·
·sin α
δ
…
·
·sinα
·
·
,
·sin α
δ
.
(3)
Если принять в качестве независимых переменных активную мощность генератора
и модуль его переходной ЭДС , а зависимых – угол ЭДС δ, то матрица Якоби будет
иметь следующий вид:
…
…
…
…
. (4)
Матрицу СВП ЭДС эквивалентных генераторов идентифицируем по результатам рас-
чета электромеханических переходных процессов, полученным с помощью ПВК Мустанг.
Параметры исходного режима, полученного для актуальной матрицы СВП ЭДС ге-
нераторов, для последующего утяжеления представлены в таблице 1.
Таблица 1 – Параметры исходного режима для актуальной матрицы СВП
ЭДС генераторов
Номер
узла
Наименование
, МВт , кВ , МВар
δ, рад
1 РефтГРЭС 703,4 522,0 527,6 0,0000
2 Тюмень 1 203,0 556,1 262,2 0,2067
3 СГРЭС-2 4 800,0 546,7 1 428,8 0,4947
4 СГРЭС-1-220 1 165,0 583,3 791,9 0,1114
5 НВГРЭС 865,0 583,5 523,5 0,3980
6 СГРЭС-1-500 2 008 545,4 593,4 0,4185

217
В расчетах утяжеления за базисный узел принималась Рефтинская ГРЭС, и после-
довательно утяжелялся каждый из пяти узлов эквивалента.
В ходе расчетов предельных мощностей генерирующих узлов по условиям стати-
ческой апериодической устойчивости на основе актуальной матрицы СВП при постоян-
ных ЭДС генераторов получены меньшие предельные мощности генерирующих узлов,
чем при расчетах по полной схеме замещения (таблица 2). Разница объясняется тем, что
при расчете по полной схеме замещения в промышленной программе учтена работа регу-
ляторов возбуждения генераторов, ограничения по допустимой загрузке оборудования и
напряжению в электрической сети.
Таблица 2 – Предельные активные мощности генерирующих узлов
Номер
узла
Наименование
пред
, МВт
Расчет по полной
схеме замещения
ЭЭС
(ПВК Мустанг)
Расчет по матрице
СВП напряжений
генерирующих узлов
(ПВК Мустанг)
Расчет по актуальной матрице
СВП ЭДС генерирующих узлов
(модель «нерегулируемой» ЭС)
2 Тюмень 6 044,61 4 670,19 3 660,8
3 СГРЭС-2 6 789,84 6 137,50 5 889,1
4 СГРЭС-1-220 3 179,26 2 504,45 2 405,6
5 НВГРЭС 2 845,27 2 195,47 1 857,2
6 СГРЭС-1-500 3 993,74 3 341,59 3 123,6
Выводы
1. Для мониторинга запасов статической устойчивости в темпе процесса целесооб-
разно двухэтапное представление послеаварийного режима ЭЭС с выделением кратко-
временного квазиустановившегося режима непосредственно после затухания электроме-
ханических процессов и собственно длительного послеаварийного режима. Для каждого
из этапов полезно получение пределов по устойчивости и их использование в системе ПА.
2. Для квазиустановившегося
послеаварийного режима предельные режимы следу-
ет определять по условиям статической устойчивости, а для послеаварийного дополни-
тельно учитывать ограничения по допустимости загрузки оборудования и напряжения в
электрической сети.
3. Определение предельных режимов по статической устойчивости для квазиуста-
новившегося послеаварийного режима в СМПР может эффективно производиться по ак-
туальной матрице СВП ЭДС эквивалентных генераторов при постоянстве переходных ЭДС.
Список использованных источников
1. Чебан В.М. и др. Управление режимами электроэнергетических систем в аварийных ситуациях:
Учеб. Пособие для электроэнергет. спец. вузов / В.М. Чебан, А.К. Ландман, А.Г. Фишов. М.:
Высш.шк.,1990. 144с.
2. Идельчик В.И. Расчеты установившихся режимов электрических систем. М.: Энергия, 1977.
192 с.
3. Методические указания по устойчивости энергосистем. Утв. Приказом
Минэнерго России от
30.06.2003 №277
4. Аюев Б.И., Жуков А.В. Новые подходы к мониторингу запаса устойчивости электроэнергети-
ческих систем // Энергосистема: управление, конкуренция образование. Сб. докл. III межд. на-
уч.-практ. конф. В 2 т. Екатеринбург: УГТИ-УПИ, 2008. Т. 1. 453 с.

218
ОПТИМИЗАЦИОННАЯ МОДЕЛЬ ПРЕДЕЛЬНЫХ
ПО СУЩЕСТВОВАНИЮ РЕЖИМОВ ЭЛЕКТРИЧЕСКИХ СИСТЕМ
Б.И. Аюев, В.В. Давыдов, П.М. Ерохин
ОАО «СО ЕЭС»
Режим электрических систем (ЭС) подвержен различным возмущениям – флуктуа-
ция нагрузки, изменение топологии, аварийное (плановое) отключение (включение) элек-
трооборудования и т.д. – и требуется знать пределы изменений как с точки зрения стати-
ческой устойчивости установившегося режима (УР) ЭС, так и его существования.
В промышленных программах предельные режимы (ПР) обычно находятся многократным
расчетом УР в заданном направлении утяжеления [1, 2]. Этот подход надежен и прост в
реализации, но, поскольку используется идеология метода «проб и ошибок», время расче-
та ПР в значительной мере определяется заданием шага утяжеления. Существенным вкла-
дом в теорию предельных режимов явилось формирование уравнений предельных режи-
мов (УПР) [3, 4], в которых уравнения УР (УУР) с заданным направлением утяжеления
решаются совместно с уравнениями, обеспечивающими линейную зависимость строк или
столбцов матрицы Якоби. Хотя этот подход по точности и быстродействию превосходит
методы последовательного утяжеления [4], он страдает существенным недостатком – для
успешной реализации требуется хорошее начальное приближение собственного вектора и
предельного режима в пространстве комплексов напряжения. Плодотворное развитие ме-
тодов нелинейного программирования и вычислительной техники дали мощный толчок
использованию оптимизационных постановок для решения задач, связанных с предель-
ными режимами [5–7]. Однако большинство работ или ограничивается нахождением пре-
дельных режимов в заданном направлении утяжеления, или реализуемые условия опти-
мальности не содержат в явном виде критерия предельных режимов, поэтому нет гаран-
тий, что будут получены ожидаемые ПР.
Основная черта существующих подходов расчета ПР заключается в добавлении к
вычислительной модели УР «внешних» критериев ПР. Как следствие, требуется либо
большой объем вычислений, либо не гарантируется робастность алгоритмов. Вместе с тем
критерий ПР содержится в самой вычислительной модели УР. ПР является, прежде всего,
УР, но некоторые
его параметры принимают предельные (экстремальные) значения.
Рассмотрим особенности вычислительных моделей УР и их ПР на примере УУР в
форме баланса мощностей в полярной системе координат [8]
∆
, , δ
cosδ
sinδ
0,
∆
, , δ
cosδ
sinδ
0,
(1)
где
, δ
,
,
– модуль, фазовый угол комплекса напряжения, активная и реактивная
мощности узла ;
– элемент матрицы узловых проводимостей; δ
δ
δ
– разность фазовых углов между смежными узлами и .
Систему нелинейных уравнений (1) можно представить в компактной форме
∆, 0, (2)
где ∆, , , – соответственно векторы небалансов мощностей, зависимых и незави-
симых переменных. Разделение на независимые и зависимые переменные отражает тот
факт, что число переменных (параметров) в системе (2) превышает количество уравнений.
219
С математической точки зрения отнесение к зависимым и независимым перемен-
ным может быть произвольным, определяется только количество зависимых переменных,
значения которых могут быть получены из решения (2) при известных независимых пере-
менных. С точки зрения расчета УР к независимым переменным относятся те, для кото-
рых имеется конкретная информация, а именно, мощности узлов и модули напряжений
генераторов, оснащенных системой АРВ. Комплексы напряжений относятся к зависимым
переменным, которые находятся из решения (2).
Отметим важное свойство УУР. Изменение всех фазовых углов на одну и ту же ве-
личину не изменяет значение правой части. Поэтому система (1) имеет бесконечное мно-
жество решений. Необходимо задать точку отсчета, для чего фазовый угол одного из уз-
лов, который получает название базисного, должен быть зафиксирован, т.е. переведен
в состав независимых переменных. Поскольку число зависимых переменных становится
на единицу меньше числа уравнений, математическая формализация требует пополнить
их число. В силу специфики энергосистем в качестве таковой принимается активная мощ-
ность одного из узлов, который становится балансирующим по активной мощности. Вы-
бор базисного узла может быть произвольным. Выбор балансирующего узла (БУ) связан
со спецификой ЭС.
Решение системы нелинейных уравнений (2) можно рассматривать как отображе-
ние независимых переменных в пространство зависимых переменных
[9]. Со-
гласно теореме о неявной функции необходимым условием существования такого ото-
бражения и, следовательно, решения системы нелинейных уравнений (2) является невы-
рожденность матрицы частных производных системы нелинейных уравнений (2) по зави-
симым переменным
∆
⁄
. В УУР (1) мощности узлов входят аддитивно. Если не
брать во внимание технологические ограничения на параметры режима, система (1) будет
всегда совместной при любых фазовых углах и модулях напряжений при условии, что
мощности узлов вычисляются непосредственно из (1). Поэтому предельный по существо-
ванию режим ЭС можно охарактеризовать как режим, в котором при малом изменении
независимых переменных система уравнений (1) становится несовместной, т.е. неразре-
шимой относительно зависимых переменных. Теорема о неявной функции утверждает,
что если в УР с параметрами
,
расчетная матрица не вырождена, то для любого
достаточно близкого к
существует единственное
, являющееся решением не-
линейных УУР ∆
, 0. Поэтому следствием теоремы о неявной функции явля-
ется, во-первых, необходимое условие предельного по существованию режима – вырож-
денность матрицы
∆
⁄
[10], а во-вторых, существование близких вторых решений в
окрестности предельного режима [11].
Согласно теореме Сарда множество нерегулярных значений
переменных, т.е. когда
расчетная матрица вырождена, имеет (лебегову) меру нуль [12]. Дополнение ко всякому
множеству нулевой меры является всюду плотным. Следовательно, каждая точка про-
странства переменных сколь угодно близка к некоторому регулярному значению отобра-
жения. С одной стороны теорема Сарда гарантирует практическую невозможность полу-
чения непредельного режима с вырожденной расчетной матрицей (точки перегиба), т.е.
делает необходимое условие получения ПР достаточным. С другой стороны она говорит о
том, что расчетные ПР будут только приближением к действительным предельным режимам.
В ряде случаев вообще невозможно строго получить вырожденную расчетную мат-
рицу Якоби. Так, например, для двухузловой схемы с узлами (см. рисунок), с БУ
расчетной матрице Якоби соответствует выражение
∆
δ
⁄
|
|
cos
δ
α
, (3)
где
|
|
– модуль проводимости ветви, соединяющей узлы и ; α
arctg
⁄
– угол потерь полного сопротивления ветви .
