Сборник докладов - Электроэнергетика глазами молодежи 2010
Подождите немного. Документ загружается.


220
Рисунок – Двухузловая схема
Нулевое значение (3) получается для δ
2
α
. Число π является иррацио-
нальным, поэтому получить «чистый» ноль в (3) практически нельзя. В других случаях
расчетные матрицы хоть и будут в малой окрестности зависимых переменных плохо обу-
словленными, но почти всегда невырожденными. Это свойство, в принципе, обеспечивает
робастность метода Ньютона по параметру. Если рассчитывается несуществующий ре-
жим, то в методе Ньютона по параметру итерационный процесс сходится к предельному
режиму с «вырожденной» расчетной матрицей. Теоретически нельзя решать систему ли-
нейных уравнений с вырожденной матрицей, но это реализуется в методе Ньютона по па-
раметру [1], а значит, в предельном режиме расчетная матрица, как правило, не вырожде-
на. Предельный режим можно сравнить с «крутым обрывом». Вычислительные модели
вдали от предела практически не чувствуют край обрыва и могут «улететь» достаточно
далеко за предел [3], что требует дополнительных страховочных механизмов.
Вырожденность расчетной матрицы Якоби, а следовательно, и ПР зависит от со-
става зависимых и независимых переменных. Приняв их состав в соответствии с вычисли-
тельной моделью УУР, рассмотрим типовую задачу оптимизации режима энергосистемы
, min (4)
при условии
∆, δ,
∆
, δ,
∆, δ,
0
0
0
. (5)
Система (5) – это УУР (1) в векторной форме. Функция цели определяется решае-
мой задачей, например, суммарный расход топлива, затраты на выработку электрической
энергии, общее благосостояние и т.д. В задаче оптимизации (4)–(5) все оптимизируемые
переменные равнозначны. Однако из-за особенности УУР в одном из узлов должен быть
зафиксирован фазовый угол напряжения. Других ограничений нет. В классической теории
нелинейного программирования разделение на зависимые и независимые переменные не
используется. Оно было введено при разработке алгоритмов метода приведенного гради-
ента [13] для задачи оптимизации режимов ЭС. На основе теоремы о неявной функции
оптимизируемые переменные были сгруппированы в зависимые и независимые перемен-
ные, что позволило значительно сократить сложность решения задачи, разделив ее на две
подзадачи – расчет режима (решение системы уравнений (5)) и шаг оптимизации в про-
странстве независимых переменных. Однако чтобы связать решение задачи (4)–(5) с пре-
дельным режимом, условно разделим оптимизируемые переменные на зависимые и неза-
висимые переменные аналогично тому, как принято при расчете УУР. Индексом услов-
но обозначен БУ. В задаче оптимизации это может быть любой узел, участвующий в оп-
тимизации.
Сформируем функцию Лагранжа
, , δ, , λ
, λ
,
∆
, δ,
λ
∆
, δ,
λ
∆
, δ,
λ
.
(6)
|
|
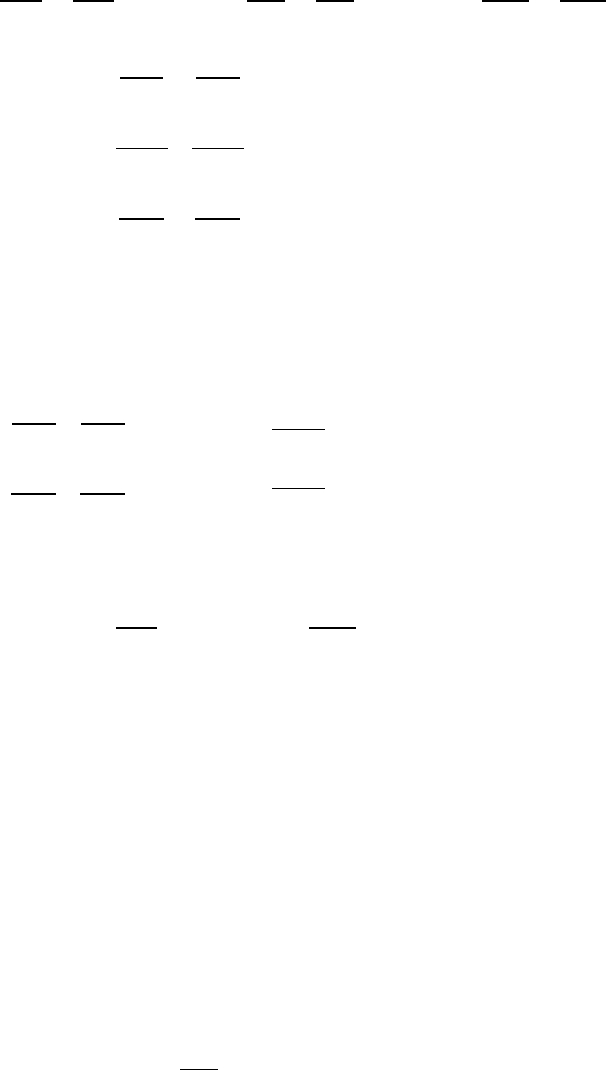
221
Запишем необходимые условия получения оптимального решения (4)–(5) – равен-
ство нулю градиента функции Лагранжа (6) по всем оптимизируемым переменным:
λ
0;
λ
0;
λ
0;
(7)
∆
δ
∆
∆
δ
∆
∆
δ
∆
λ
λ
λ
0
; (8)
∆, δ,
0
;
∆
, δ,
0
;
∆, δ,
0
.
(9)
Представив систему (8) в виде
∆
δ
∆
∆
δ
∆
λ
λ
∆
δ
∆
λ
(10)
и используя теорему о неявной функции, можно получить соотношение между множите-
лями Лагранжа
λ
1
П
λ
, λ
П
λ
, (11)
где П
⁄
, П
⁄
– относительные приросты потерь активной мощности по активной
и реактивной мощности узла , которые позволяют дать важную интерпретацию пре-
дельных по существованию режимов ЭС.
Рассмотрим продажу электрическими станциями электроэнергии на оптовом рын-
ке, где в качестве целевой функции используется выражение
∑
min. Здесь
– заявочная цена -й станции за киловатт-час отпущенной электроэнергии.
Предположим, что у мощной ГЭС в узле переполнено водохранилище и необхо-
димо в «холостую» сбросить воду, либо продать электроэнергию по любой цене. ГЭС за-
являет низкую цену. Предположим также, что в результате сетевой ремонтной компании
ослаблена пропускная способность линий, отходящих от станции. До какой степени будет
загружена ГЭС в результате торгов? Это определяется соотношениями (7) и (11), которые
для данного случая примут вид
λ
1
Π
. (12)
Считая, что
, получаем 1П
⁄
⁄
0. Когда ГЭС анонсирует
нулевую цену, λ
0 и П
⁄
1, т.е. станция загружена так, что последующее
увеличение ее активной мощности будет идти только на вызываемые этим потери. Если
при расчете УР такая станция не является балансирующей, режим не будет предельным,
так как возможна дополнительная загрузка ее и других узлов. Поскольку относительный
прирост активных потерь станции превысит единицу, дальнейшая
ее загрузка приведет
к снижению полезно полученной мощности, которую восполнит БУ. Если при расчете УР

222
данная станция назначена балансирующей, режим будет предельным по существованию.
Действительно, в этом случае система (10) примет вид
λ
0, (13)
∆
δ
∆
∆
δ
∆
λ
λ
0
0
(14)
Матрица левой части системы (14) является расчетной матрицей Якоби УУР, а по-
скольку условие (14) при λ
, λ
0 определяет ее вырожденность, это соответствует ПР
ЭС. Назначение нулевой цены для узла соответствует исключению его мощности из целе-
вой функции. Поэтому, если активную мощность узла, выполняющего функции баланси-
рующего при расчете УР, не включать в целевую функцию (4), решением оптимизацион-
ной задачи (4)–(5) будет ПР, отвечающий заданной целевой функции.
Таким образом, ПР можно охарактеризовать как невозможность БУ поддержать
режим ЭС, поскольку все его действия по балансировке режима при малом его изменении
будут сведены на нет возникающими при этом потерями активной мощности. БУ как бы
теряет электрическую связь с частью или со всей ЭС, что соответствует отсутствию БУ в
вычислительной модели УР со всеми вытекающими последствиями.
Исключение из целевой функции (4) компонент, в явном виде содержащих зависи-
мые переменные УУР (1)–(2), не нарушает условия о допустимости использования функ-
ции Лагранжа и существования неявной функции в ПР. Действительно, согласно теории
нелинейного программирования [14], чтобы гарантировать существование и единствен-
ность вектора множителей Лагранжа, градиенты уравнений ограничений (5) должны быть
линейно независимы. В задаче оптимизации (4)–(5) количество переменных превышает
число уравнений связи (5). Поэтому однородная система линейной зависимости градиен-
тов имеет больше условий, чем переменных. В соответствии с теоремой Сарда, ненулевое
решение такой системы, т.е. линейная зависимость градиентов, имеет «лебегову» меру
нуль [9, 12]. Линейная независимость градиентов уравнений (5) обеспечивает выполнение
условия существования неявной функции
в ПР, но не для узла, который назначается ба-
лансирующим при расчете ПР, а для узлов, имеющих ненулевые множители Лагранжа
в (14). При смене балансирующего узла в ПР условие (13)–(14) в общем случае не будет
выполняться, если только претендент на балансирующий узел не имеет нулевой множи-
тель Лагранжа в системе (10).
В качестве иллюстрации
рассмотрим утяжеление режима двухузловой схемы,
представленной на рисунке, – увеличение на одну и ту же величину генерации в узле и
нагрузки в узле . Если узел балансирующий, то расчетный предельный режим будет
соответствовать максимальной выдачи мощности из узла , т.е. когда матрица Якоби (3)
будет вырождена. Если в этом предельном режиме переназначить балансирующим узел ,
то расчетная матрица
∆
δ
|
|
cos
δ
α
(15)
будет невырожденной. Поэтому можно воспользоваться теоремой о неявной функции и
режим не будет предельным. Таким образом, для одного и того же направления утяжеле-
ния, но при разном выборе БУ, существует два разных ПР с δ
2
α
или δ
2
α
.
223
В существующих промышленных программах расчет ПР ведется, как правило,
с одиночным БУ. Поэтому в зависимости от расположения БУ и траектории утяжеления
возможно получение ПР, отвечающего как максимальной выработке, так и максимально-
му потреблению. При этом технолог не будет знать, какому случаю соответствует ПР.
Возможна третья альтернатива, когда ПР будет вызван достижением предельного
транзитного потока мощности от БУ, компенсирующего увеличение потерь активной
мощности в процессе утяжеления. Технолог об этом не догадается, если не воспользуется
дополнительным инструментарием, например [15].
С точки зрения ведения режима предпочтительным является получение ПР, отве-
чающего максимально возможной нагрузке. Одним из подходов устранения неоднознач-
ности и получения требуемого ПР является использование распределенного БУ, вклю-
чающего только утяжеляемые генераторы с коэффициентами участия, пропорциональные
соответствующим компонентам вектора утяжеления. В этом случае увеличение нагрузки,
в том числе возникающие при этом потери активной мощности, будут покрываться только
участвующими в утяжелении генераторами и ничем другим. ПР будет отвечать макси-
мально возможной величине нагрузки для заданной траектории утяжеления, а критиче-
ское сечение, характеризующее ПР, – району утяжеления.
Из-за ограничений на объем статьи расчетные формулы с распределенным БУ не
представлены. С ними можно ознакомиться в работе [16]. Следует отметить, что расчет
ПР в заданном направлении с распределенным БУ может быть достаточно легко реализо-
ван в существующих промышленных программных комплексах расчета УР, поскольку
вычислительные модели режима с распределенным БУ и с учетом частоты практически
совпадают, а расчет последнего, как правило, реализован в этих комплексах.
В случае отсутствия в двухузловой схеме, представленной на рисунке, активных со-
противлений предельный режим будет один. Для любой консервативной ЭС ПР останется
предельным при любом переназначении балансирующего узла [16]. Но это не значит, что
условия существования неявной функции в задаче оптимизации будут нарушены. Раннее
отмечалось, что в нелинейном программировании все переменные считаются равнознач-
ными. Зависимые и независимые переменные вводятся, когда используется теорема о не-
явной функции. В предельном режиме для консервативной ЭС при применении неявной
функции возможный состав зависимых переменных будет включать мощности не менее
двух узлов.
Выводы
1. Предложена оптимизационная модель предельных режимов ЭС, необходимые
условия оптимальности которой соответствуют математическому критерию предельного
режима ЭС.
2. В предельном режиме любые попытки балансирующего узла поддержать режим
полностью компенсируются возникающими при этом потерями активной мощности. Не-
способность балансирующего узла поддержать режим ряда узлов определяет предельный
по существованию режим ЭС.
3. Предельный режим зависит от принятого состава зависимых и независимых пе-
ременных, в частности, от назначенного балансирующего узла. В зависимости от распо-
ложения балансирующего узла и траектории утяжеления возможны три альтернативы
предельного режима. Для разрешения неоднозначности и получения требуемого предель-
ного режима следует использовать концепцию распределенного балансирующего узла.
4. В консервативной ЭС предельный режим останется предельным при любом пе-
реназначении балансирующего узла.
224
Список использованных источников
1. Venikov V.A., Stroev V.A., Idelchik V.I., Tarasov V.I. Estimation of power system steady
state stability in load flow calculations // IEEE Transactions on PAS. - vol. PAS-94, no. 3,
May/June, 1975. P.1034–1041.
2. Ajjarapu V., Christy C., The continuation power flow: a tool for steady state voltage stabili-
ty analysis // IEEE Transactions on Power Systems (далее TPWRS), Vol . 7, No. 1, Febru-
ary 1992, P.416–423.
3. Конторович А.М., Крюков А.В. Предельные режимы энергосистем (основы теории и
методов расчета): учебное пособие. Иркутск, Иркутский ун-т, 1985, 72 с.
4. Canizares C. A., Alvarado F. L., DeMarco C. L., Dobson I., Long W. F. Point of collapse
method applied to ac/dc power systems // TPWRS, Vol. 7, No. 2, May 1992, P.673–683.
5. Давыдов В.В., Крюков А.В., Сактоев В.Е. Оценка запасов устойчивости и определе-
ние допустимых режимов энергосистем. Депонировано в ИНФОРМЭНЕРГО №3002-
эн88, 1989. Восточно-Сибирский технологический институт, 11 с.
6. Custem T.V. A method to compute reactive power margins with respect to voltage collapse
// TPWRS, Vol . 6, No. 1, February 1991, P.145–156.
7. Zarate L.A., Castro C.A., Ramos J.L.M., Ramos E.R. Fast computation of voltage stability
security margins using nonlinear programming techniques // TPWRS, Vol . 21, No. 1, Feb-
ruary 2006, P.19–27.
8. Вычислительные мотели потокораспределения в электрических системах / Б.И. Аюев,
В.В. Давыдов, П.М. Ерохин, В.Г. Неуймин; под. ред. П.И. Бартоломея. М.: Флинта:
Наука, 2008. 256 с.
9. Ортега Д., Рейнболд В. Итерационные методы решения нелинейных систем уравне-
ний со многими неизвестными. М.: Мир, 1975. 558 с.
10. Идельчик В.И. Предел по существованию решения уравнений установившегося ре-
жима // Вопросы применения математических методов при управлении режимами и
развитием электрических систем. Иркутск: иркутский политехн. ин-т, 1975. С. 6–21.
11. Обен Ж.-П., Экланд И. Прикладной нелинейный анализ: Пер. с англ. М.:Мир,1988.
512 с., ил.
12. Брус Дж., Джиблин П. Кривые и особенности: Геометрическое введение в теорию
особенностей: пер. с англ. М.: Мир, 1988. 262 с.
13. Крумм Л.А. Методы приведенного градиента при управлении электроэнергетически-
ми системами. Новосибирск: Наука, 1977. 368 с.
14. Бертсекас Д. Условная оптимизация и методы множителей Лагранжа: пер. с англ. М.:
Радио и связь, 1987. 400 с.
15. Давыдов В.В., Неуймин В.Г., Сактоев В.Е. Определение критических сечений энерго-
систем в предельных режимах // Известия РАН. Энергетика. 1992. №1. С. 74–80.
16. Аюев Б.И., Давыдов В.В., Ерохин П.М. Оптимизационная модель предельных режи-
мов электрических систем // Электричество, 2010, №11.

225
ОСОБЕННОСТИ РАСЧЕТА ЗАПАСОВ СТАТИЧЕСКОЙ
УСТОЙЧИВОСТИ В РЕЖИМЕ РЕАЛЬНОГО ВРЕМЕНИ
А. И. Дехтерев, А. Г. Фишов
ГОУ ВПО «НГТУ»
В рамках реформирования электроэнергетики России идет процесс создания рынка
электроэнергии и перехода на рыночные отношения между производителями и потреби-
телями электроэнергии, поэтому в настоящее время особенно актуально повышение эко-
номической эффективности работы энергосистемы без снижения надежности. Одним из
способов повышения экономических показателей работы энергосистемы является ослаб-
ление сетевых ограничений, а именно увеличение максимально допустимых (МДП) и ава-
рийно допустимых (АДП) перетоков в контролируемых сечениях. Традиционный метод
расчета предполагает заблаговременное определение МДП для наиболее тяжелых про-
гнозных схемно-режимных условий, вероятность которых мала, что приводит к недоис-
пользованию пропускной способности сети и снижению экономических показателей ра-
боты энергосистемы.
Новые возможности предоставляет внедряемая в настоящее время в ЕЭС России
система синхронизированных векторных измерений (система регистрации переходных
режимов) [1–3]. СМПР является хорошим инструментом для создания системы монито-
ринга запасов устойчивости (СМЗУ), работающей в режиме реального времени (on-line) и
учитывающей текущие схемно-режимные условия работы энергосистемы.
В работе [3] были представлены результаты исследования возможности идентифи-
кации матрицы собственных и взаимных проводимостей (СВП) как модели электрических
связей генерирующих узлов энергосистемы на основе данных СМПР в режиме on-line без
контроля топологии и параметров электрической сети с последующим определением за-
пасов статической устойчивости. Матрица СВП может быть определена из известных вы-
ражений при измерении прямым и косвенным образом мощностей и изменений мощно-
стей отдельных генераторов, переходных ЭДС и углов расхождения роторов генераторов
системы [4]:
cosδ
sinδ
,
;
sinδ
cosδ
,
,
(1)
где
,
– активная и реактивная (с учетом потерь в сопротивлении генератора) мощно-
сти -го генератора;
,
– собственные активная и реактивная проводимости -го гене-
ратора;
,
– взаимные активная и реактивная проводимости между генераторами и ;
– переходная ЭДС -го генератора; δ
– взаимный угол переходных ЭДС генераторов
и (δ
δ
).
Выражения, описывающие изменения мощности на валу отдельно взятого генера-
тора при малом изменении угла:
∆
∆δ
sinδ
cosδ
,
;
∆
∆δ
cosδ
sinδ
,
,
(2)
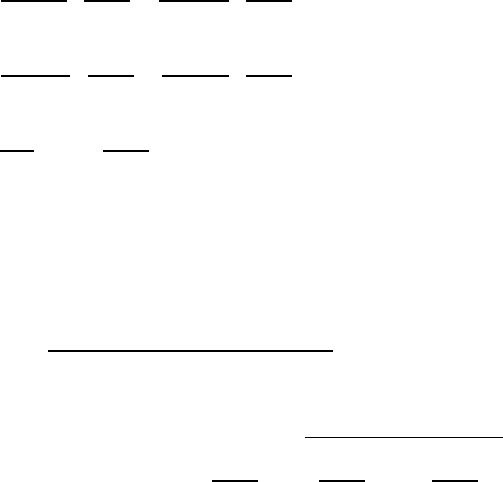
226
где ∆
, ∆
– изменение активной и реактивной мощностей -го генератора; ∆δ
– изме-
нение взаимного угла переходных ЭДС генераторов и , причем необходимо учесть, что
∆δ
∆δ
.
Для случаев, когда число неизвестных матрицы СВП больше четырех, недостаю-
щие уравнения могут быть получены по выражениям (1) и (2) для замеров режимных па-
раметров в разных точках переходного процесса. Необходимым условием получения не-
достающих уравнений является значимое изменение режимных параметров во времени
таким образом, чтобы уравнения (1), (2), составленные для различных замеров, были ли-
нейно независимыми. В реальной энергосистеме это условие обычно выполняется в по-
слеаварийных режимах при значимых электромеханических колебаниях (интервал обу-
словленности, как правило, составляет 2–5 с), а также в нормальных режимах за счет не-
регулярных колебаний.
Сложность определения матрицы СВП заключается в нестабильности расчетных
значений проводимостей в процессе ее идентификации, вызывающей большие погрешно-
сти в определении запасов статической устойчивости.
В работе [5] был проведен анализ условий идентификации матрицы СВП на при-
мере простейшей схемы «генератор с собственной нагрузкой – ШБМ». В качестве одного
из факторов рассматривался набор уравнений из выражений (1) и (2), входящих в систему
уравнений для определения СВП, так как необходимым условием является равенство чис-
ла уравнений и числа неизвестных проводимостей. Результаты экспериментов показали,
что погрешность определения СВП из системы уравнений, составленной только по выра-
жениям (1), меньше, чем при совместном использовании выражений (1) и (2) [5]. Также
было отмечено, что погрешность определения СВП в первом случае практически не зави-
сит от величины изменения взаимного угла между переходной ЭДС генератора и напря-
жением шин бесконечной мощности.
В результате решения системы уравнений, составленной из выражений (1) и (2) для
простейшей схемы, собственная и взаимные проводимости можно определить по сле-
дующим выражениям (выражение для собственной реактивной проводимости
не при
водится, так как она не влияет на расчет пределов выдаваемой мощности генератора):
С
sinδ
ГС
Г
С
∆
Г
∆δ
ГС
cosδ
ГС
Г
С
∆
Г
∆δ
ГС
; (3)
С
cosδ
ГС
Г
С
∆
Г
∆δ
ГС
sinδ
ГС
Г
С
∆
Г
∆δ
ГС
; (4)
1
Г
Г
∆
Г
∆δ
ГС
, (5)
где
С
– напряжение шин бесконечной мощности.
Учитывая полученные выражения, собственная мощность генератора
и макси-
мум взаимной мощности
С max
будут определяться по выражениям:
Г
∆
Г
∆δ
ГС
⁄
; (6)
С max
∆
Г
∆δ
ГС
⁄
∆
Г
∆δ
ГС
⁄
. (7)
Тогда пределы выдаваемой мощности генератора можно определить по выражению
lim
С max
Г
∆
Г
∆δ
ГС
∆
Г
∆δ
ГС
∆
Г
∆δ
ГС
, (8)
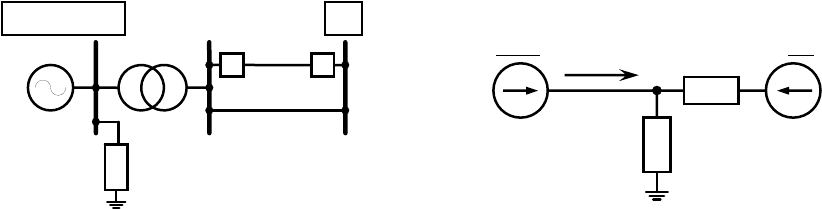
227
где знак «+» соответствует максимуму выдаваемой мощности (верхний предел), а знак «–»
– максимуму принимаемой узлом мощности (нижний предел), т.е. узлом сети, где нахо-
дится рассматриваемый генератор.
Из выражения (8) следует, что предел выдаваемой мощности генератора в значи-
тельной степени определяется значением отношений изменений активной и реактивной
мощностей соответственно к изменению взаимного угла между переходной ЭДС генера-
тора и напряжением ШБМ.
Таким образом, использование выражений (2) при составлении уравнений для
идентификации матрицы СВП имеет недостаток, связанный с тем, что в процессе элек-
тромеханических колебаний имеются участки, где изменение взаимного угла незначи-
тельно (∆δ
С
0). В этом случае отношения изменений мощностей генератора к измене-
нию взаимного угла становятся неопределенными, вследствие этого в расчетах пределов
выдаваемых мощностей возникают большие погрешности.
Ниже представлены результаты расчета пределов выдаваемой мощности генерато-
ра при использовании выражений (1) и (2).
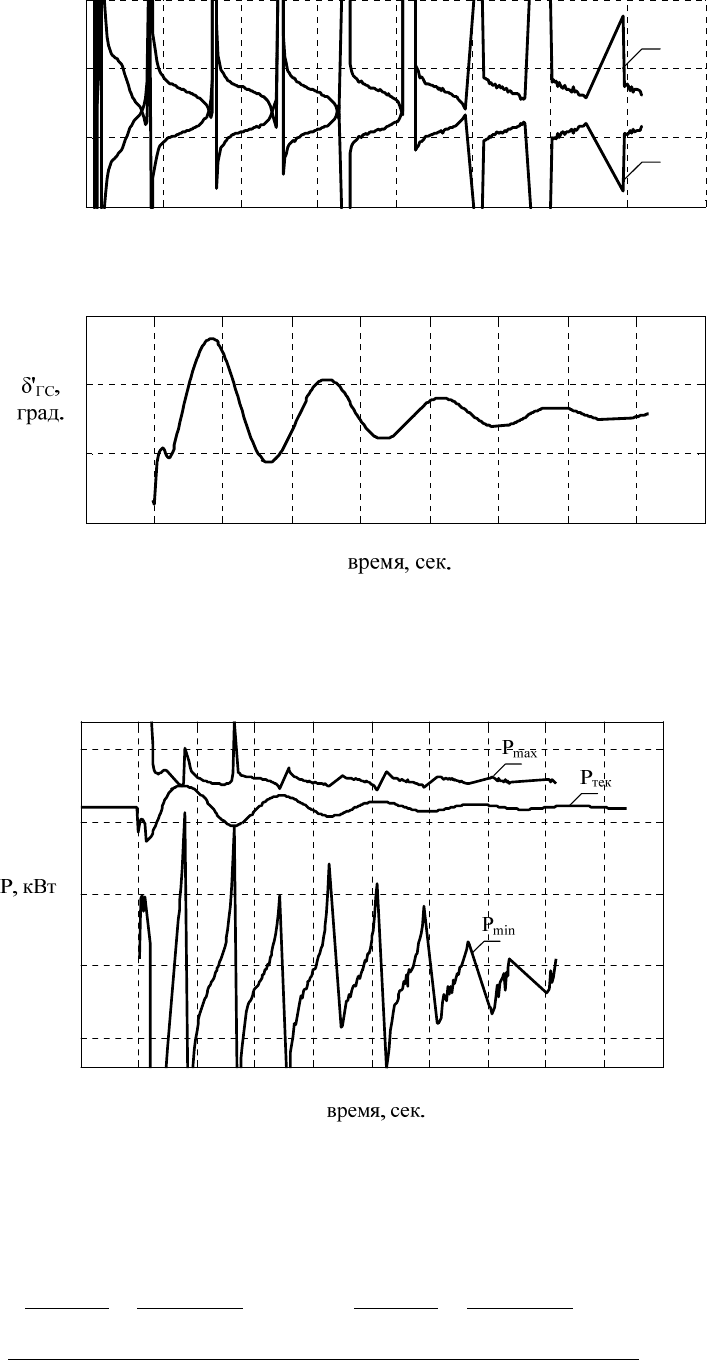
По программе Mustang моделировалась простейшая схема «генератор с собствен-
ной нагрузкой – ШБМ», изображенная на рисунке 1.
а б
Рисунок 1 – Генератор с собственной нагрузкой – ШБМ
а – принципиальная схема; б – схема замещения
Генератор представлялся по уравнениям Парка-Горева. Нагрузка замещалась по-
стоянными сопротивлениями. Для получения изменения режимных параметров в качестве
возмущающего воздействия принималось двухфазное короткое замыкание (КЗ) на одной
линии с последующим отключением.
После расчета электромеханического переходного процесса производился расчет
пределов выдаваемой мощности по специально разработанной программе в пакете Matlab.
Результаты оценки собственной и взаимной мощности генератора (а), а также изменение
взаимного угла δ
ГС
(б) представлены на рисунке 2 (момент КЗ – = 1 с).
На рисунке 2, а наглядно показаны недостатки использования выражений (2) для
определения пределов выдаваемых мощности. Оценки верхнего
max
и нижнего
min
пре-
делов выдаваемой мощности в режиме реального времени с использованием выраже-
ний (1) и (2) приведены на рисунке 3, где
тек
– текущее значение активной мощности ге-
нератора.
Таким образом, при использовании выражений (2) для составления системы урав-
нений с целью идентификации матрицы СВП, пригодной для дальнейшего применения,
оказывается только оценка верхнего предела выдаваемой мощности. Для сглаживания по-
лученной оценки верхнего предела может быть использован метод фильтрации, описан-
ный в [5], который основан на принципе скользящего среднего с контролем выбросов.
ШБМ
Г
нагр
,,,δ
С
Г
Г
Г
|δ
С
|0
228
а
б
Рисунок 2 – Электромеханический переходный процесс:
а – оценки собственной и взаимной мощностей генератора; б – изменение взаимного
угла между переходной ЭДС генератора и напряжением ШБМ
Рисунок 3 – Оценка пределов выдаваемой мощности (1 вариант)
Использование при составлении системы уравнений только выражений (1) дает
лучшие результаты. В этом можно убедиться, рассмотрев выражения, полученные для
взаимных проводимостей
в результате решения соответствующей системы уравнений:
С
Г
Г
Г
Г
∆
Г
Г
Г
Г
∆
∆
∆
; (9)
0 1 2 3 4 5 6 7 8 9
20
40
60
80
1 2 3 4 5 6 7 8 9
-10
0
10
20
P
11
P
1С max
время, сек.
P
11
, кВт
P
1С max,
кВт
0 1 2 3 4 5 6 7 8 9 10
-10
-5
0
5
10
229
С
Г
Г
Г
Г
∆
Г
Г
Г
Г
∆
∆
∆
; (10)
∆
С
Г
sinδ
ГС
С
Г
sinδ
ГС
;
∆
С
Г
cosδ
ГС
С
Г
cosδ
ГС
,
где
– номер выборки.
После проведения преобразований знаменатель выражений (9), (10) можно пред-
ставить в следующем виде:
∆
∆
С
Г
С
Г
2
С
С
Г
Г
1 cosδ
ГС
δ
ГС
. (11)
Если принять, что напряжение ШБМ неизменно, то из (11) следует, что знамена-
тель в выражениях (9), (10) будет равен нулю только при одновременном выполнении
двух условий: постоянство ЭДС и взаимного угла в промежутке между двумя выборками.
«Относительное постоянство» или малое изменение указанных параметров возможно при
их переходе через свои локальные экстремумы. На практике большинство генераторов ос-
нащены автоматическими регуляторами возбуждения сильного действия. При правильной
настройке такой регулятор действует с упреждением, поэтому переходная ЭДС генерато-
ра пройдет свой локальный экстремум раньше, чем взаимный угол. Следовательно, усло-
вие равенства нулю знаменателя в выражениях для взаимных проводимостей (9), (10), а
также для определения собственных проводимостей, в большинстве случаев не выполня-
ется, поэтому система уравнений, составленная только из выражений (1), будет давать бо-
лее точные решения по сравнению с системой уравнений, составленной по выражениям
(1) и (2). Расчет пределов выдаваемой мощности производился по выражению:
lim
Г
Г
С
, (12)
где знак «+» соответствует максимуму выдаваемой мощности (верхний предел), а знак «–»
– максимуму принимаемой узлом мощности (нижний предел), т.е. узлом сети, где нахо-
дится рассматриваемый генератор.
Результат оценки пределов выдаваемой мощности в режиме реального времени с
использованием второго варианта системы уравнений представлен на рисунке 4.
На рисунке 4
max ор
и
min ор
– соответственно верхний и нижний пределы выда-
ваемой мощности согласно выражению (12), полученные с использованием СВП, рассчи-
танных по известным параметрам схемы, представленной на рисунке 1а. Как видно из ри-
сунка 4, использование только выражений (1) для составления системы уравнений дает
более стабильные результаты. Для сглаживания оценки нижнего предела также может
быть использован метод
фильтрации, приведенный в работе [5].
Колебания оценки пределов выдаваемой мощности являются особенностью расче-
тов, проводимых в режиме реального времени. Эти колебания связаны с работой регуля-
тора возбуждения генератора. В результате отклонения напряжения на выводах генерато-
ра регулятор начинает менять ЭДС возбуждения, таким образом, меняется расчетное зна-
чение переходной ЭДС, поэтому, несмотря на
постоянство СВП в электрической схеме,
согласно выражению (12), происходит изменение пределов выдаваемой мощности.
