Савина Н.В. Применение теории вероятности и методов оптимизации в системах электроснабжения

Подождите немного. Документ загружается.

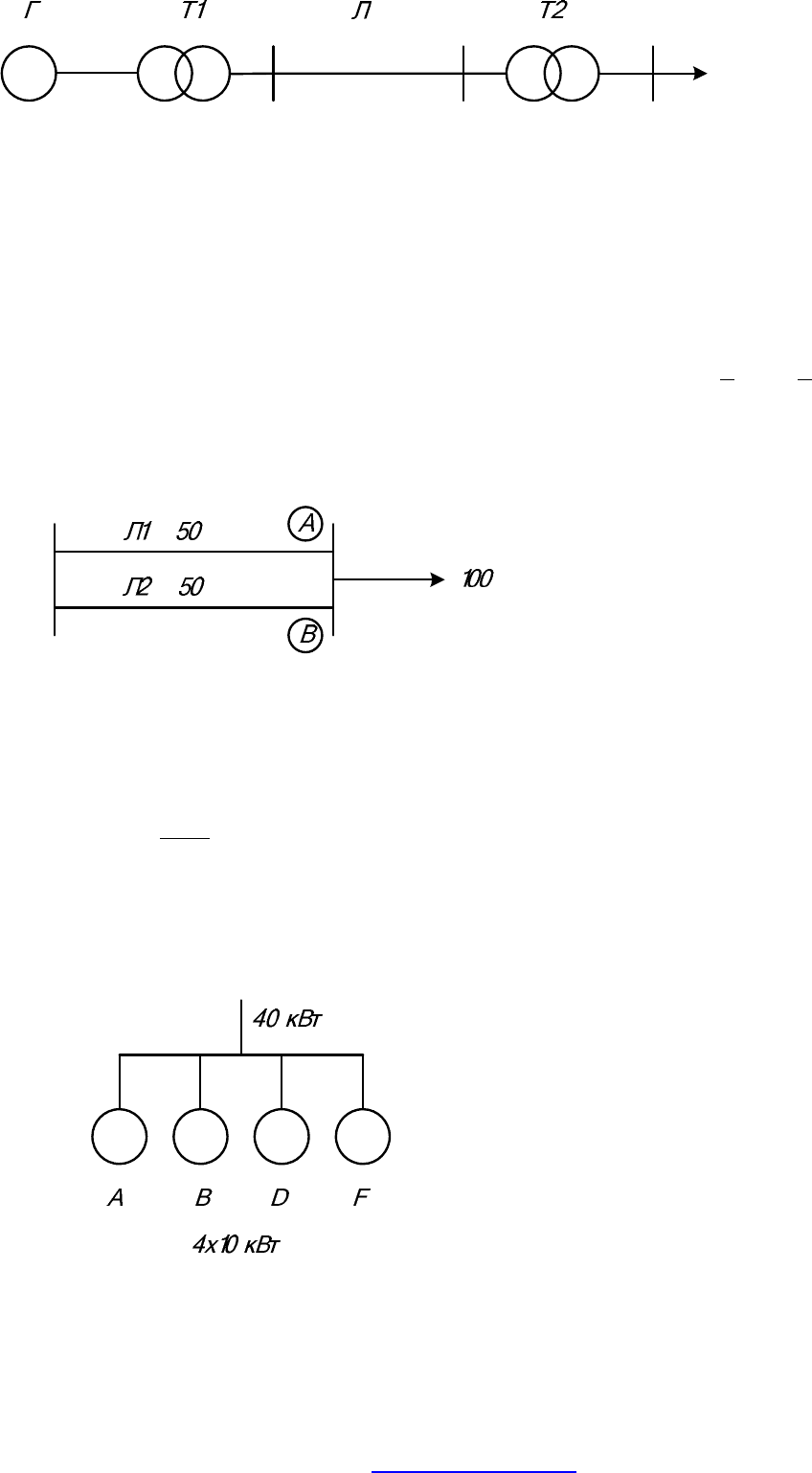
Рис. 8. Схема электрической сети

Произведением двух событий А и В называют событие С, состоящее в

совместном выполнении события А и события В.

Например: ЭП получает требуемую мощность 100 МВт, если и

, и

работают (рис. 9):

САВ

Рис. 9.

Произведением нескольких событий называют событие, состоящее в

совместном появлении всех этих событий. Для схемы, приведенной на рис. 10,

40 кВт - событие С, будет на вводе силовой сборки, если одновременно будут

работать все четыре двигателя, то есть

CABDF

Рис. 10.

PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

Независимые случайные события

Теорема сложения вероятностей несовместных событий

Вероятность суммы двух несовместных событий А и В равна сумме

вероятностей этих событий:

р(А+В) = р(А)+р(В). (6)

Докажем теорему, пользуясь классическим определением вероятности /4/.

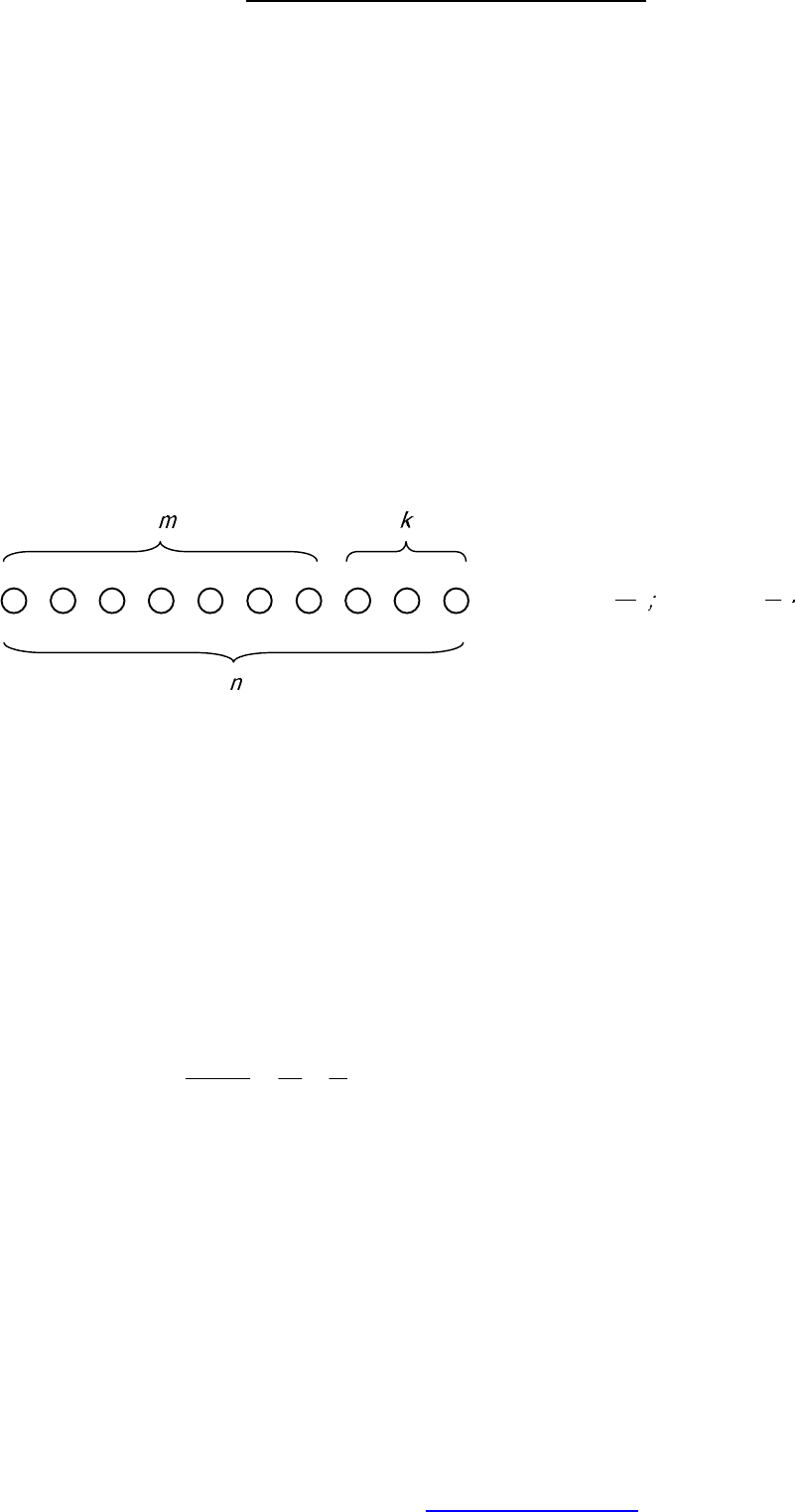
Если из общего числа исходов в опыте – числа возможных случаев n в m

случаях событие А происходит, а в k случаях происходит событие В, (см. рис.

11), то

()

Рис. 11.

Так как события «А» и «В» несовместны, то нет таких случаев, которые

благоприятны появлению событий А, и В вместе, т.е. случаи, входящие в число

m, не входят в число k и наоборот. Вероятность того, что происходит одно из

событий А или В, очевидно, будет:

()()()

mkmk

pABpApB

nnn

+==+=+ - теорема доказана.

Эта формула распространяется на сумму произвольного числа случаев:

()()

pApA

∑∑

. (7)

PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

Следствия:

1) Если события

AA ...

образуют полную группу несовместных событий,

то сумма их вероятностей равна 1:

()1

∑

, (8)

т.е. в полной группе одно из событий обязательно произойдет.

2) Сумма вероятностей противоположных событий равна 1:

()()1

pApA

. (9)

Мы будем пользоваться этим при анализе надежности системы

электроснабжения: p+q=1, то есть, зная вероятность рабочего состояния

элемента (системы), можно определить вероятность отказа и наоборот.

Теорема умножения вероятностей

Вероятность произведения двух независимых событий равна

произведению вероятностей этих событий:

р(АВ) = р(А)р(В). (10)

Пусть событие А происходит в m случаях из общего числа случаев n,

когда событие А может произойти или не произойти, а событие В – в k случаях

из общего числа случаев ℓ. Тогда

()

; ()

В любом случае из указанного числа n может произойти ℓ различных

случаев возникновения или невозникновения В. Всего число возможных

случаев составляет nℓ. В каждом случае возникновения события А (число таких

случаев m) может произойти k случаев одновременного возникновения события

В. Всего число случаев одновременного возникновения А и В будет mk.

PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

Поэтому вероятность одновременного возникновения событий А и В

равна

()()()

pABpApB

, что и требовалось доказать.

Если события А и В несовместимы, то р(АВ)=0.

Аналогично можно доказать, что вероятность произведения n

независимых событий равна произведению вероятностей этих событий:

()()

pApA

∏∏

. (11)

Теорема сложения вероятностей независимых совместных событий

Вероятность суммы двух независимых совместных событий А и В равна

сумме их вероятностей без произведения вероятностей этих событий:

р(А+В)=р(А)+р(В)-р(АВ). (12)

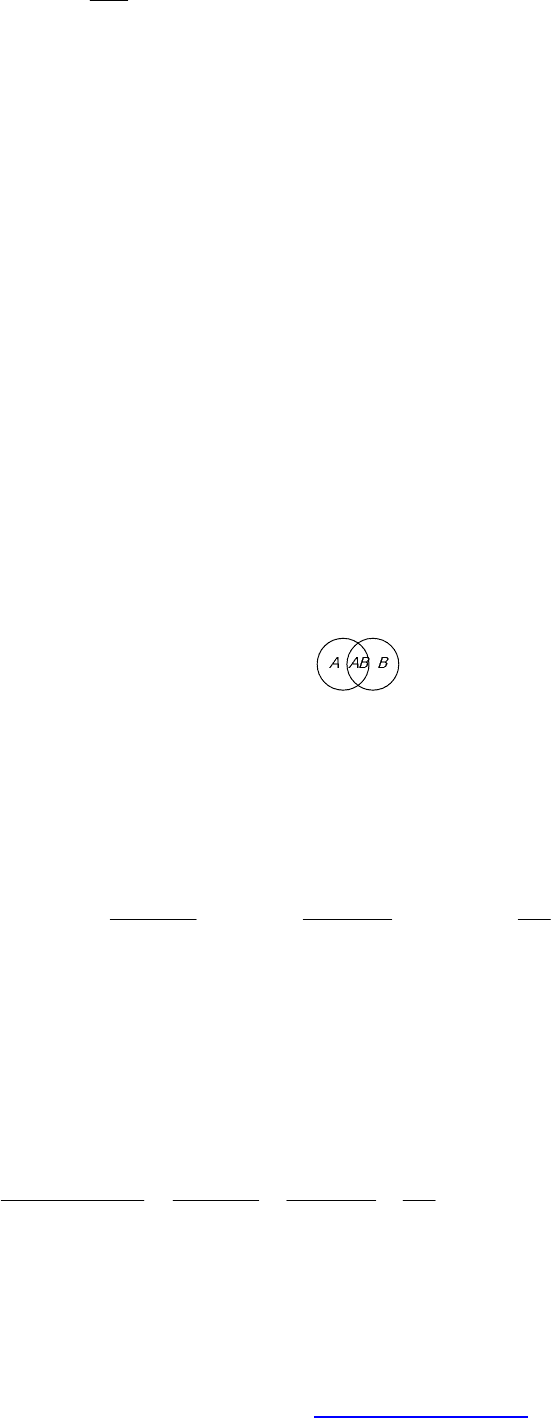
Если события А и В изобразить окружностями, то доказательство

формулы можно представить рисунком .

Пусть из общего числа случаев n в

случаях происходит только

событие

, в

случаях – событие В, в

случаях – события А и В

одновременно. Тогда

()

= ;

()

= ;

()

pAB

= .

Очевидно, общее число случаев, когда имеет место событие А или В (хотя

бы одно из них), составляет m

, т.е. вероятность суммы двух

совместных событий будет:

12313233

()()()()

mmmmmmmm

pABpApBpAB

nnnn

++++

+==+−=+− .

Т.к.

313

mmm

≤+

323

mmm

≤+

, то

()()

pABpA

≤

()()

pABpB

≤

PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

Для n событий

...

вероятность суммы n совместных событий равна

алгебраической сумме вероятностей произведений комбинаций этих событий

по два, по три, по четыре, …, по n:

121

1111111

()()()()...(1)()

nnnnnnn

iiijijki

iiijiijikj

pApApApApA

−−−

−

====+==+=+

=−+−+−

∑∑∑∑∑∑∑

∏

. (13)

Доказать это выражение можно методом полной индукции. Его

иллюстрация для трех событий характеризуется рисунком

A B

CA BC

ABC

Здесь окружности А, В, С выражают вероятности событий А, В, С.

Таким образом, для трех событий

р(А+В+С)=р(А)+р(В)+ р(С)-р(А)р(В) -р(А)р(С) -р(В)р(С) + р(А)р(В)р(С).

Зависимые случайные события

Пусть два события А и В являются зависимыми. Это означает, что

вероятность наступления одного из них изменится, если произойдет другое

событие. Для оценки этого вводится понятие условной вероятности.

Определим чему равна условная вероятность р(А/В), используя для

простоты классическое определение вероятности. Пусть из общего числа

случаев n событие А наступит в m случаях, В – в k случаях, событие АВ

(одновременное наступление событий А и В) – в ℓ случаях. Очевидно, что

≤≤

. Событие В происходит только в k случаях и при этом только в ℓ из

k случаев происходит событие А, поэтому условная вероятность события А по

отношению к В равна

/()

(/)

/()

npAB

pAB

kknpB

===

PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

То есть условная вероятность события А по В при их совместимости и

взаимозависимости равна отношению вероятности одновременного

наступления событий А и В к вероятности события В, причем

(/)()()

pABpApB

≠

Вероятность события А, вычисленная при условии, что имело место

другое событие В, называется условной вероятностью события А и

обозначается р(А/В).

Пример: повреждение отдельных фаз ЛЭП. При повреждении одной

фазы ЛЭП в сети с незаземленной нейтралью (изолированная нейтраль)

напряжения других фаз увеличиваются в

раз, что повышает вероятность

повреждения других фаз.

Теорема умножения вероятностей зависимых событий

Вероятность произведения двух зависимых событий равна

произведению вероятности одного из них на условную вероятность другого,

вычисленную при условии, что первое имело место:

р(АВ)=р(А)р(В/А);

р(АВ)=р(В)рА/В). (14)

Докажем теорему для схемы случаев (рис.12).

Пусть возможные исходы опытов сводятся к n случаям, которые мы

снова для наглядности изобразим в виде n точек.

→

Рис. 12.

PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

Предположим, что событию А благоприятны m случаев, а событию В – k

случаев. Так как события А и В совместны, то существуют случаи

благоприятные и событию А, и событию В одновременно. Пусть число таких

случаев равно ℓ.

Тогда ()pAB

; ()

Вычислим условную вероятность события В в предположении, что

событие А имеет место – р(В/А).

Если известно, что событие А произошло, то из ранее возможных n

случаев остаются возможными только те m, которые благоприятствовали

событию А. Из них ℓ случаев благоприятны В. Следовательно, (/)pBA

Подставляя р(АВ), р(А), р(В/А) в выражение (14) получим тождество

nnmn

=⋅=

lll

что и требовалось доказать

Следствие: Если событие А не зависит от события В, то и событие В не

зависит от события А, то есть

р(А)р(В/А)=р(В)р(А/В). (15)

Для n событий

,...

ААА

вероятность произведения n событий равна

произведению вероятности события А на условные вероятности последующих

событий

,...

ААА

, вычисленные при условии, что предыдущие события имели

место:

123121312121

(...)()(/)(/)...(/...)

nnn

pAAAApApAApAAApAAAA

−

=⋅

. (16)

При использовании теорем умножения и сложения вероятностей в

решении практических задач следует руководствоваться простым правилом:

«Если в цепи рассуждений, приводящих к ответу на поставленный в задаче

PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

вопрос, логически получается союз «или», то применяется теорема сложения,

если союз «и» – теорема умножения».

Формула полной вероятности

Пусть требуется определить вероятность сложного события А,

подразделяемого на частные случаи В

, В

и В

, при зависимости А от В

, В

Тогда Р(А) =

Р(А/В

)·Р(В

)+Р(А/В

)·Р(В

)+Р(А/В

)·Р(В

). Данное выражение

называется формулой полной вероятности.

Докажем ее: пусть требуется определить вероятность некоторого события

А, которое может произойти вместе с одним из событий В

, В

, …, В

образующих полную группу несовместных событий. Будем эти события

называть гипотезами.

Докажем, что в этом случае Р(А)=

∑

Р(В

) ·Р(А/В

), то есть вероятность

события А вычисляется как сумма произведений вероятности каждой гипотезы

на вероятность события при этой гипотезе.

Так как гипотезы В

, В

, …, В

образуют полную группу, то событие А

может появиться только в комбинации с какой - либо из этих гипотез:

А=В

А+В

А+…+В

А.

Так как гипотезы несовместны, то и комбинации

А, В

А,…, В

А также

несовместны. Применим к ним теорему сложения

Р(А)= Р(В

А)+Р(В

А)+…+Р(В

А)=

∑

i 1

Р(В

А).

Используя для события В

А теорему умножения, получим

Р(А)=

∑

i 1

Р(В

) ·Р(А/В

), что и требовалось доказать.

PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

1.3. Схема независимых испытаний – частная теорема о повторении

опытов

В системах электроснабжения события, как правило, наблюдаются в

результате повторения одних и тех же независимых опытов или серии

аналогичных опытов. Под независимыми опытами (сериями) понимаются

опыты (серии), в которых вероятность ожидаемого события не зависит от

вероятности этого же события, но в других опытах или сериях. Примером

повторения одних и тех же опытов является циклическая работа ЭП.

Продолжительность одного опыта равна t

, а ожидаемыми событиями являются

включение ЭП с вероятностью К

и его отключение с вероятностью К

Примером серии опытов является циклическая работа четырех ЭП, представ-

ляемая четырьмя сериями опытов. В каждой из серий опытов события включе-

ния ЭП происходят с разными вероятностями: К

В1

, К

В2

, К

В3

, К

В4

В практических задачах электроснабжения целью расчета является опре-

деление общего числа m, вероятности р

, средней длительности t

и частоты

возникновения ожидаемых m событий в результате n повторений опытов

или серий аналогичных опытов. Однако вероятности событий от опыта к

опыту или в каждой из серий аналогичных опытов могут быть одинаковыми

или различными. В первом случае для определения характеристик m событий

применяется частная теорема о повторении опыта – биноминальное

распределение вероятностей, во втором - общая теорема о повторении опытов.

Частная теорема о повторении опытов или схема независимых

испытаний

При большом числе однотипных агрегатов в ЭЭС или СЭС вероятности

повторения различного числа агрегатов могут быть определены по

биноминальной формуле вероятности для схемы независимых испытаний –

схемы Бернулли. Ее также называют частной теоремой о повторении опытов

опытов.

Во многих практических случаях при многократных независимых

испытаниях могут быть только два исхода: случайное событие А произойдет

PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

или не произойдет. Пусть вероятность того, что в каждом из этих независимых

испытаний произойдет событие А, равна р. Тогда вероятность

противоположного события (А не происходит ) равна q.

Зная р и q, можно определить вероятность того, что в n независимых

испытаниях событие произойдет m раз. Обозначим эту вероятность р

. Она

равна произведению числа комбинаций из n по m на вероятность события А в

степени n и на противоположную вероятность в степени (n-m). Тогда

вероятность рабочего состояния m элементов системы из n может быть

определена по формуле:

( )

mmmnmmnm

рCpqpq

mnm

−−

−

. (17)

Вероятность отказа m элементов из n:

( )

mmmnmmnm

qCqpqp

mnm

−−

−

, (18)

данное выражение называется формулой Бернулли или формулой

биноминального распределения.

Очевидно, что

∑

=1, так как эта сумма охватывает все возможные

события (m варьирует от 0 до n).

Для того, чтобы получить эту формулу, рассмотрим выражение (р+q)

Оно равно 1, так как р и q вероятности противоположных событий и образуют

полную группу событий. Разлагая n-ю степень бинома (р+q)

в ряд по

известному закону, получим:

(п+q)

= q

+n·q

n-1

· р+ С

·q

n-2

· P

+…+ С

·q

n-m

· P

+ …+р

=1. (19)

Здесь (m+1)-й член разложения определяет вероятность рабочего

состояния m элементов из n, равную С

· р

·q

(n-m)

PDF создан испытательной версией pdfFactory Pro www.pdffactory.com