Самусевич Г.А. Теория вероятностей в примерах и задачах. Теория вероятностей и математическая статистика
Подождите немного. Документ загружается.

1
Федеральное агентство по образованию
Уральский государственный технический университет – УПИ
имени первого Президента России Б.Н. Ельцина
Г.А. Самусевич
Теория вероятностей в примерах и задачах
Теория вероятностей и математическая статистика
Учебное пособие
Научный редактор проф., канд. техн. наук Д.В. Астрецов
Печатается по решению
Редакционно-издательского совета УГТУ – УПИ от 07.04 2009 г.
Екатеринбург
УГТУ-УПИ
2009
2
УДК 519.8
ББК 22.17
С17
Рецензенты: Уральский технический институт связи и информатики
(зам. зав. кафедрой общепрофессиональных дисциплин технических специ-
альностей доц., канд. техн. наук Н.В. Будылдина)
Российский государственный профессионально-педагогический уни-
верситет (проф. кафедры общей физики, докт. физ- мат наук А.Д. Ивлиев)
Самусевич Г.А.
С17 Теория вероятностей в примерах
и задачах : учебное пособие/
Г.А. Самусевич. Екатеринбург: УГТУ – УПИ. 2009. 80 с.
ISBN 978-5-321-01427-1
Представленная работа является пособием по решению задач по тео-
рии вероятностей и математической статистике. Предназначена прежде все-
го для самостоятельной работы студентов. Содержит задачи, решаемые в
течение ряда лет, на практических занятиях на радиотехническом факульте-
те УГТУ – УПИ для
студентов специальностей: «Средства связи с подвиж-
ными объектами», «Радиоэлектронные системы» и «Информационная без-
опасность телекоммуникационных систем».
Содержащиеся в пособии задачи охватывают все разделы теории ве-
роятностей, такие как случайные события, случайные величины, системы
случайных величин, функции случайных величин, предельные теоремы
теории вероятностей, элементы математической статистики. Решение задач
там, где это
необходимо, подробно проиллюстрировано. Представленное
пособие предназначено для самостоятельного изучения студентами предла-
гаемой дисциплины.
Библиогр.:11 назв. Рис. 51. Табл. 12. Прил. 2.
Подготовлено кафедрой «Радиоэлектронные и телекоммуникацион-
ные системы».
УДК 519.8
ББК 22.17
ISBN 978-5-321-01427-1 ©УГТУ– УПИ, 2009
© Самусевич Г.А., 2009
3
Оглавление
1. Случайные события ........................................................................................ 4
1.1. Основные понятия теории вероятностей ............................................ 4
1.2. Алгебраические операции над событиями .......................................... 6
1.3. Непосредственный подсчет вероятностей ......................................... 15
1.4. Частная теорема о повторении опытов .............................................. 21
1.5. Надежность .............................................................................................. 22
1.6. Формула полной вероятности .............................................................. 25
1.7. Теорема гипотез (формула Байеса) ..................................................... 28
2. Случайные величины ..................................................................................... 32
2.1. Дискретные случайные величины ...................................................... 32
2.2. Непрерывные случайные величины .................................................. 35
3. Наиболее часто встречающиесязаконы распределения
случайных
величин ................................................................................................................. 39
3.1. Биномиальное распределение. Распределение Пуассона ............... 39
3.2. Показательное распределение .............................................................. 43
3.3. Равномерное и нормальное распределения ....................................... 46
4. Системы двух случайных величин .............................................................. 52
4.1. Система дискретных случайных величин. ........................................ 52
4.2. Система непрерывных случайных величин ..................................... 57
4.3. Двумерное нормальное распределение .............................................. 61
5. Функции случайных величин ....................................................................... 62
5.1. Функции одного дискретного случайного аргумента ..................... 62
5.2. Функция одного непрерывного случайного аргумента .................. 64
5.3. Композиция законов распределения .................................................. 67
6. Оценки числовых характеристик .............................................................. 71
6.1. Оценки математического ожидания и дисперсии ........................... 72
6.2. Точность оценок математического ожидания и дисперсии ........... 73
6.3. Оценка вероятности по частоте ........................................................... 75
БИБЛИОГРАФИЧЕСКИЙ СПИСОК ............................................................ 78
Приложение 1 ..................................................................................................... 79
Приложение 2 ..................................................................................................... 80

4
1. Случайные события
1.1. Основные понятия теории вероятностей
[1, разд. 1.1, 1.2.1, 1.2.3, 1.2.4, с. 5-9, 11-13]
Пространством элементарных событий (исходов) называется
множество Ω – множество взаимоисключающих исходов:
таких, что в результате опыта должен произойти один из ис-
ходов;
в рамках данного опыта нельзя разделить элементарный исход
на более мелкие исходы;
появление одного исхода исключает появление
других.
Каждое событие рассматривается как некоторое подмножество
множества Ω.
Если опыт сводится к схеме случаев, то вероятность события А
равна отношению
n
m
AP
a
)( , (1.1)
где
a
m – число случаев, благоприятных событию А; n – общее чис-
ло случаев (более подробно смотри ниже в разделе 1.3).
Задача 1.1
Игральная кость подбрасывается один раз.
Х – число очков, выпавших
на верхней грани. Описать множество элементарных исходов и указать со-
став подмножеств, соответствующих приведенным событиям, вычислить
значения вероятностей этих событий.
= {
1
,
2
, …,
6
} – n-мерное множество элементарных исходов (со-
бытий).
n = 6.
События, рассматриваемые как подмножества множества :
События Подмножества Вероятности событий
А = {Х кратно двум};
А = {
2
,
4
,
6
};
() 3/6PA
;
В
= {Х нечетно};
В = {
1
,
3
,
5
};
() 3/6PB ;
С
= {Х больше 2};
С = {
3
,
4
,
5,
6
};
() 4/6
PC ;
D
= {Х не больше 4};
D = {
1
,
2
,
3,
4
};
() 4/6PD ;
E
= {Х меньше 8};
E = ;
;1)(
E
P
F = {Х не меньше 3};
F
= {
3
,
4
,
5,
6
};
() 4/6PF ;
5
Задача 1.2
Игральная кость подбрасывается дважды. Наблюдаемый результат –
пара чисел (
i, j), соответствующая числам очков, выпавших в первый и во
второй раз. Описать подмножества, соответствующие приведенным собы-
тиям. Вычислить значения вероятностей этих событий.
События:
А = {оба раза выпало число очков, кратное двум};
В = {ни разу не выпало число один};
С = {оба раза выпало число очков, больше двух};
D = {оба раза выпало одинаковое число очков};
E = {первый раз выпало число 5, во второй – меньше пяти}.
Решение задачи
=
{( , ) / 1 , 6}ij ij
– 36 – мерное множество элементарных исходов.
События рассматриваются как подмножества множества . Приведе-
ны их вероятности.
(2,2); (2,4); (2,6); (4,2); (4,4); (4,6); (6, 2); (6,4); (6,6) , ( ) 9/36;APA
( , )/ 2 , 6 , 25, ( ) 25/ 36;
B
Bij ij m PB
( , ) / 2 , 6 , 16, ( ) 16/ 36;
C
Cij ij m PC
(,)/ 1 6 , 6, ( ) 6/36;
D
Dii i m PD
(5,1); (5, 2); (5,3); (5, 4) , ( ) 4/ 36.EPE
Задача 1.3
Монета подбрасывается три раза. Описать множество элементарных
исходов и указать состав подмножеств, соответствующих приведенным со-
бытиям. Вычислить значения вероятностей этих событий.
А = {герб выпал ровно два раза};
В = {ни разу не выпала цифра};
С = {выпало больше гербов, чем цифр};
D = {герб выпал не менее чем два раза подряд};
Решение задачи
Множество элементарных исходов
= {(Г, Г, Г); (Ц, Г, Г,); (Г, Ц, Г); (Г, Г, Ц); (Ц, Ц, Г); (Ц, Г, Ц);
(Г, Ц, Г); (Ц, Ц, Ц)};
.82
3
n
А
= {(Ц, Г, Г); (Г, Ц, Г); (Г, Г, Ц)}, 3, ( ) 3/8
A
mPA
.
В = {(Г, Г, Г)}, ( ) 1/8PB
.
С = {(Г, Г, Г); (Ц, Г, Г); (Г, Ц, Г); (Г, Г, Ц)}, () 4/8PC .
D = {(Г, Г, Г); (Ц, Г, Г); (Г, Г, Ц)},
() 3/8PD
.

6
Задача 1.4
Монета подбрасывается до первого появления герба. Наблюдаемый
результат – общее число подбрасываний. Описать множество элементарных
исходов и указать состав подмножеств, соответствующих приведенным со-
бытиям. Вычислить значения вероятностей этих событий.
А = {герб выпал при третьем подбрасывании};
В = {герб выпал не ранее, чем при третьем подбрасывании}.
Решение задачи
= {n = 1, 2,…}, А = {3}, В = {3, 4, …, n,…}.
1.2. Алгебраические операции над событиями
[1, разд. 1.2.2, с. 9-11]
Алгебраические операции над событиями совпадают с операциями
над множествами.
Наиболее часто встречающиеся операции:
1.
B
A
– включение.
Событие А влечет за собой событие В, т.е. все элементарные собы-
тия А содержатся в событии В.
2.
B
A
– эквивалентность.
Оба множества состоят из одних и тех же элементов: ,
B
A
A
B
.
3.
)( BABAC U – сумма или объединение событий.
Событие С состоит из всех элементарных событий A, В и в том
числе тех элементарных событий, которые одновременно принадлежат
событиям А и В (принадлежат
хотя бы одному из событий А или В).
4.
DAB
– произведение или пересечение событий.
Событие D состоит из элементарных событий, принадлежащих
одновременно (каждому) событиям А и В, т .е. происходит совместное
осуществление событий А
и В.
5
.
E
AB – разность событий.
Событие E состоит из элементарных событий, принадлежащих
событию А и
не принадлежащих событию В (событие А произошло, а
событие В не произошло).
6.
A
A – событие, противоположное событию А.
Задача 1.5
Пусть А, В, С – три события, наблюдаемые в эксперименте. Выразить
приведенные события в алгебре событий.
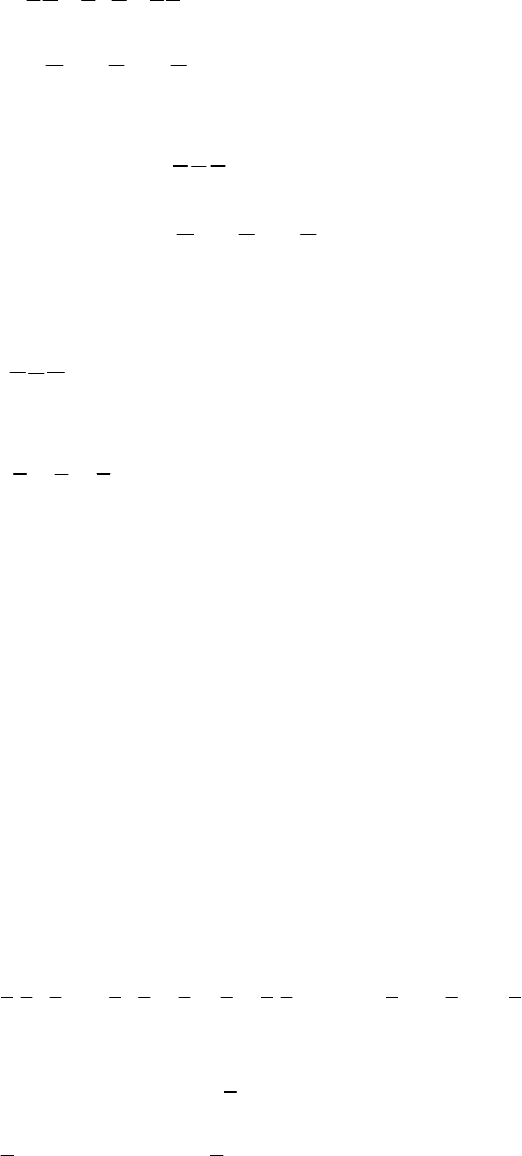
7
D
1
= {из трех событий А, B, C произойдет ровно одно событие},
D
1
= CBACBACBA .
D
2
= {произойдет ровно два события},
D
2
=
B
C
A
C
B
A
C
A
B
.
E
1
= {произойдет хотя бы одно событие} (противоположное событие
– ни одно из перечисленных событий не произойдет
),
Е
1
= A+B+C = -
A
BC .
E
2
= {произойдет не меньше двух событий} (два и более),
Е
2
=
A
B
C
BCACBACABABCD
2
.
Е
3
.= {произойдет хотя бы два события} (два и более),
E
3
= E
2
.
F
1
= {не произойдет ни одного события},
F
1
= C
B
A
.
F
2
= {не произойдет хотя бы одно событие} (противоположное – все
из перечисленных событий произойдут
),
F
2
=
A
BC ABC .
Задача 1.6
Произведено три выстрела из орудия по цели. Событие А
k
= {попада-
ние при каждом выстреле},
k = 1, 2, 3. Описать состав множества , выра-
зив элементарные исходы через события
A
k
. Записать в алгебре событий
приведенные события.
A = {произведено ровно одно попадание};
В = {произведено хотя бы одно попадание} (противоположное со-
бытие – ни одного попадания, все промахи
);
С
= {произведен хотя бы один промах} (противоположное событие –
ни одного промаха, все попадания
);
D
= {произведено не более двух попаданий} (2 и менее попаданий);
Е
= {произведено попадание не раньше, чем при третьем выстреле}.
Решение задачи
123123123123123123123123
{ , , , , , , , }
A
A A AA A AAA AAA AAA AAA AAA AAA ,
={ }
i
, i = 1, 2, … , 8.
А =
234
; В =
1
=
23 8
...
;
С =
8
=
7
1
i
i
; D =
8
= С; Е =
4
.
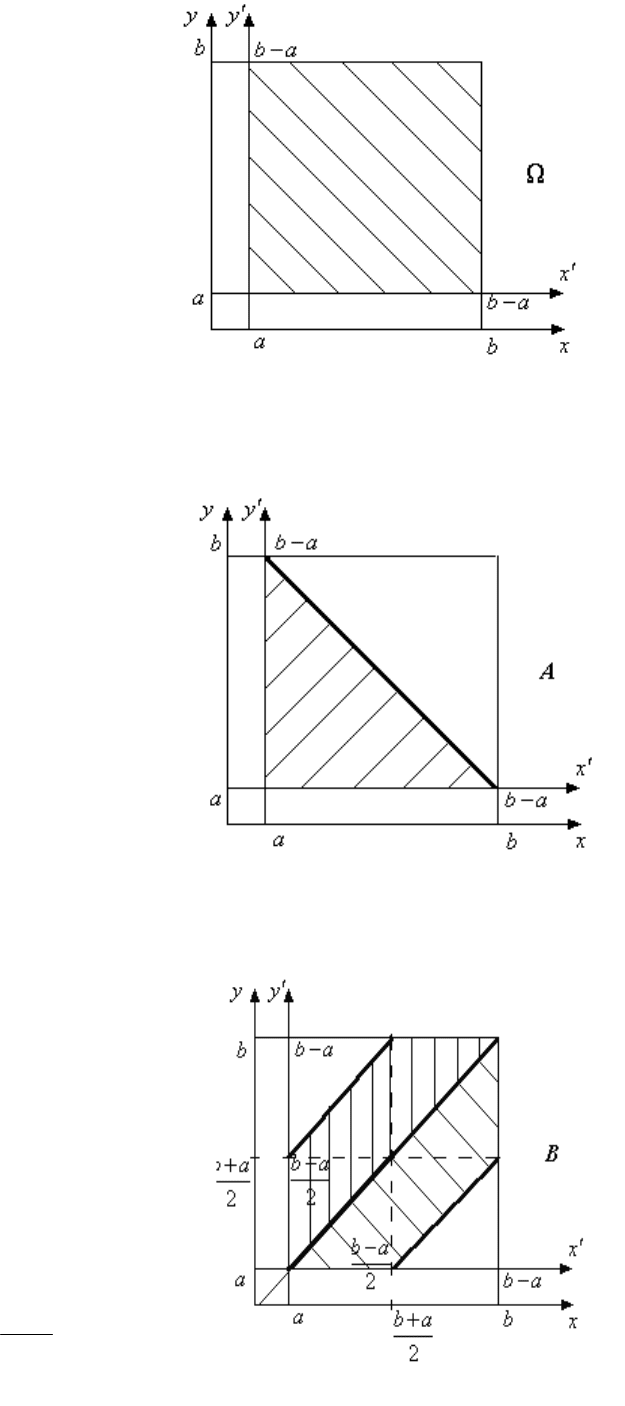
Задача 1.7
На отрезке [a,b] наудачу ставятся две точки; x и y – координаты этих
точек. Изобразить на плоскости
x0y области, соответствующие событиям
, А, В, АВ, А - В, А+В.
8
А = {вторая точка ближе к левому
концу отрезка, чем первая к правому};
В = {расстояние между точками
меньше половины длины отрезка}.
Решение задачи
На приведенных рис. 1.1 – 1.6
событиям
, A, B, А - В, А + В, АВ со-
ответствуют заштрихованные области.
Наиболее значимые границы выделены
жирной чертой.
Вводится вспомогательная систе-
ма координат, начало которой находится в точке (
a, a).
, .
x
xa y ya
Множество элементарных
исходов (рис. 1.1).
{, ,
0 , 0 }
axba yb
x
ba y b-a
.
Множество A (рис. 1.2) яв-
ляется частью множества
Удовлетво-
ряет дополнительному неравенству
yabx
, если
x
y (или
x
aby
,
если
yx ).
А
,
yabx
, abxy
.
(
()bxba xa
= bax
). .
Уравнение границы
yxba
.
Координаты контрольной точки
0xy
удовлетворяют неравенству
abxy
.
Множество B (рис. 1.3) яв-
ляется подмножеством множества
;
представляется суммой двух вариантов.
Вариант а
B
, ,
2
ba
xyxy
.
Рис. 1.1
Рис. 1.2
Рис. 1.3
9
Вариант б
B
, ,
2
ba
yxyx
.
Подробно построение области,
подобной множеству
B, будет рас-
смотрено ниже в задаче 1.10.
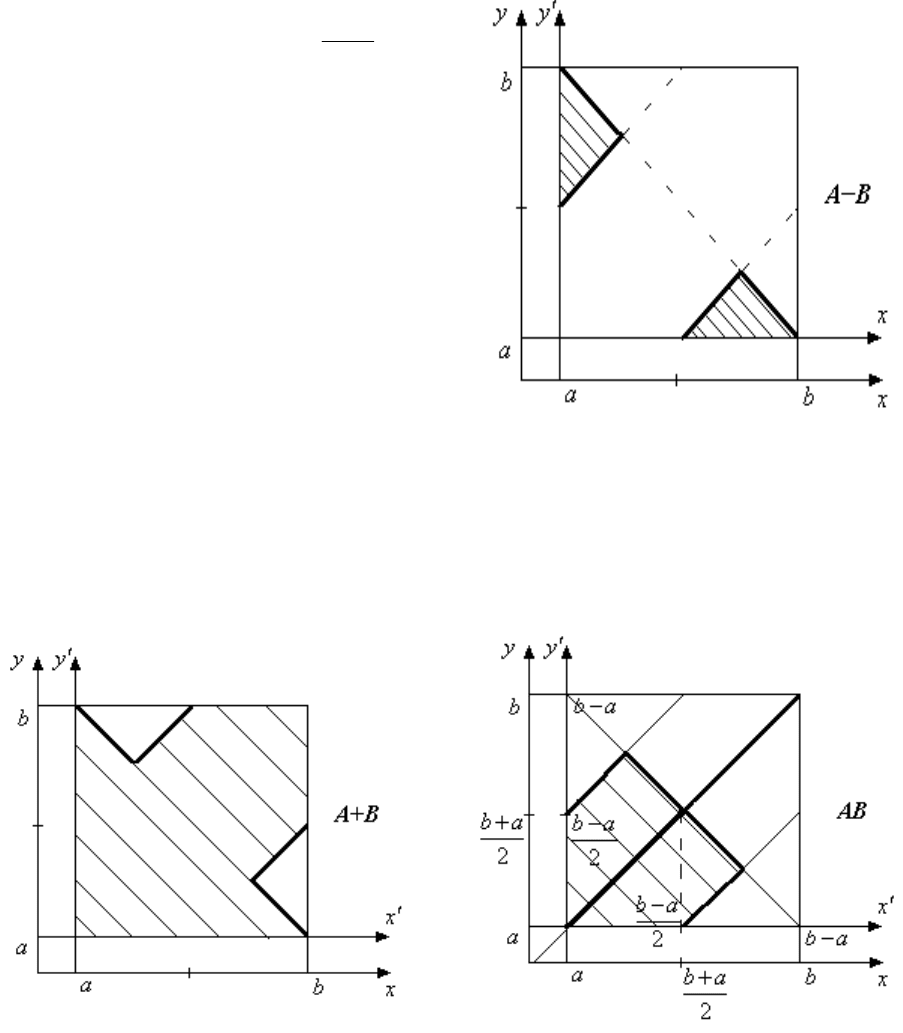
Множество A-B
(рис. 1.4) является подмножеством
множества
, содержит все элементы
множества A, не принадлежащие
множеству B.
Множество A+B
(рис. 1.5) является подмножеством
множества
, все элементы его при-
надлежат множеству A или множеству B.
Множество AB (рис. 1.6) является подмножеством множества
; содержит элементы, принадлежащие одновременно множеству A и
множеству B.
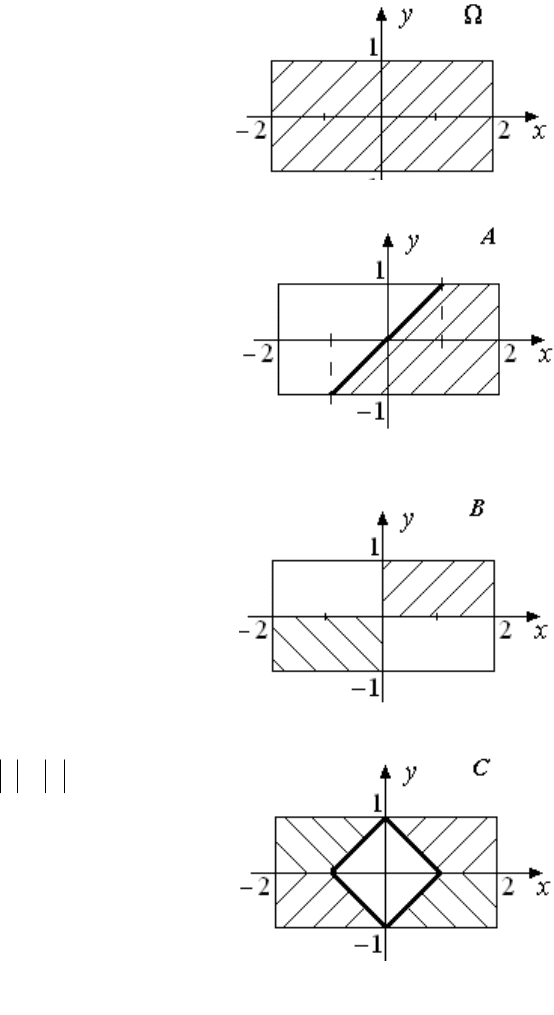
Задача 1.8
Производится стрельба по плоской прямоугольной мишени: -2 x 2,
-1
y 1. Наблюдаемый результат – координаты точки (x, y). Непопадание
в указанный прямоугольник исключено. Построить множество элементар-
ных исходов и подмножеств, соответствующих приведенным событиям.
А = {абсцисса точки попадания не меньше ординаты};
В = {произведение координат точки неотрицательно};
С = {сумма абсолютных величин координат больше единицы}.
Рис. 1.4
Рис. 1.5
Рис. 1.6
10
Решение задачи
На приведенных рис. 1.7 – 1.10 событиям , A, B, C соответствуют
заштрихованные области. Жирной линией выделены наиболее важные гра-
ницы областей.
Множество элементарных исхо-
дов
отображено на рис. 1.7.
{2 2, 1 1}
x
y
.
Подмножество, определяющее со-
бытие А, является частью множества . Все
точки этого подмножества лежат
ниже или на
выделенной границе (рис. 1.8).
А =
} ,11 ,22{ y
x
y
x
.
Подмножество, определяющее со-
бытие В, является частью множества и со-
держит только те точки, в которых значения пе-
ременных одного знака (рис. 1.9).
В =
}0 ,11 ,22{
y
x
y
x
.
Подмножество, определяющее со-
бытие С, является частью множества
(рис. 1.10). После определения границ следует
выявить допустимую область. Точки, принадле-
жащие выделенным границам, не принадлежат
подмножеству
С.
С =
,11 ,22{
y
x
}1
yx .
Уравнения границ и допустимые области:
1, 0, 0
x
yx y
;
1, 0, 0
x
yx y
;
1, 0, 0
x
yx y
;
1, 0, 0
x
yxy
.
Задача 1.9
На отрезке [a, x] ставится точка с координатой y. Наблюдаемый ре-
зультат – пара чисел (
x, y). Построить множество элементарных исходов и
подмножества, соответствующие приведенным событиям. Выявить пары
несовместных событий.
А = {точка y ближе к правому концу отрезка [a, b], чем к левому};
В = {расстояние между точками меньше половины длины отрезка};
С = {точка x ближе к точке y, чем к правому концу отрезка [a, b]}.
Рис. 1.7
Рис. 1.8
Рис. 1.9
Рис. 1.10
