Самусевич Г.А. Теория вероятностей в примерах и задачах. Теория вероятностей и математическая статистика
Подождите немного. Документ загружается.


51
Отведенный для полета самолета коридор определяется высотами:
y
0
= 0 и y
1
= 100 м. Желаемая высота полета самолета – 50 м. Случайная
величина Y – действительная высота полета имеет нормальное распределе-
ние с параметрами:
70 м; σ 75 м
x
x
m
.
0
070
( ) { } { 0} ( ) 0,3238 0,5 0,18
75
РА PY y P Y
.
01
100 70 0 70
( ) { } 0,1554 0,3238 0,4792
75 75
Р BPyYy
.
1
100 20
( ) { } {100 } ( ) 0,5 0,1554 0,3446
75
Р CPYy P Y
.
Задача 3.23
Шкала угломерного инструмента имеет цену деления в 1. Отсчет ве-
дется с точностью до целого деления с округлением в ближайшую сторону.
Х – допущенная при отсчете ошибка (с учетом знака).
а). Найти вероятность того, что допущенная при отсчете ошибка пре-
взойдет 20.
б). Какова вероятность того, что модуль допущенной ошибки не
пре-
взойдет 20?
Решение задачи
Поскольку измерения проводятся с округлением, то случайная вели-
чина Х имеет равномерное распределение на интервале (-30, 30).
10
( ) (20 30 ) 0,167;
60
PA P X
40
() ( 20) 0,667
60
PB P X
.
Задача 3.24
Диаметр Х втулок можно считать нормально распределенной величи-
ной с параметрами: а=2,5; =0,01. В какой интервал, симметричный отно-
сительно математического ожидания а, попадет случайная величина Х с
вероятностью 0,9973?
В соответствии с прил. 2 в том случае, когда функция Лагранжа
Φ(x) = 0,49865, её аргумент равен x = 3. Следовательно, с вероятностью,
равной 0,9973, нормально распределенная
случайная величина Х отклоняет-
ся от своего математического ожидания на величину, равную 3.
Таким образом, искомый интервал равен
(2,5- 3σ;2,5 3σ) (2, 47; 2,53).
J
Задача 3.25

52
На имеющемся оборудовании производятся стержни, диаметры кото-
рых можно считать нормально распределенными случайными величинами с
параметрами: а=2,0 см; =0,005 см. Диаметр приемлемых стержней не
должен выходить за рамки интервала ( 012,00,2
) см. Сколько из 5000
стержней окажутся неприемлемыми?
2,0 см; σ 0,005 см; ε 0,012 см
x
m .
ε
ε 1 ε 12
xx
x
pPXm PXm
σ
0,012
12 12 (2,4) 0,0164.
0,005
Число неприемлемых стержней равно произведению вычисленной ве-
роятности на общее число стержней (5000
p), т. е. равно 82 стержням.
4. Системы двух случайных величин
4.1. Система дискретных случайных величин
[1, разд. 4.1.1, 4.1.2, с. 59 - 63; разд.4.1.4, 4.1.5, с. 67 - 69; разд. 4.2.1, 4.2.2,
с.73- 80]
Упорядоченный набор (X, Y) случайных величин называется
двумер-
ной случайной величиной
или системой двух случайных величин.
Совместная функция распределения системы двух случайных вели-
чин
),(
Y
X
},{),( y
Y
x
X
P
y
x
F
. (4.1)
Другой формой задания совместного закона распределения (кроме
функции распределения) системы дискретных случайных величин
),(
Y
X яв-
ляется
матрица распределения – двумерная матрица размером mn
, со-
стоящая из вероятностей
ij
p
:
{ , }, 1, 2, ..., , 1, 2, ...,
ij i j
p
PX x Y y i n j m . (4.2)
Законы распределения составляющих X и Y
m
j
ijix
pxXPp
i
1
}{,
n
i
ijjy
pyYPp
j
1
}{
, (4.3)
Случайные величины Х и Y, входящие в систему, независимы, если
для всех номеров i и j справедливо равенство
ij
ij x y
p
pp. (4.4)

53
xy
K корреляционный момент случайных величин (X,Y) и коэффи-
циент корреляции
[( )( )] [ ]
x
yxy xy
K
Mxm y m MXY mm , (4.5)
yx
xy
xy
K
r
σσ
. (4.6)
Условная вероятность того, что случайная величина Y примет
значение
j
y, при условии, что
i
xX
, определяется равенством
/
{, }
/
{}
ji
i
ijij
yx j i
ix
PX x Y y p
pPYyXx
PX x p
, (4.7)
1, 2, ..., , 1, 2, ...,injm.
Аналогично,
/
{, }
/
{}
ij
j
ijij
xy i j
j
y
PX x Y y p
pPXxYy
PY y p
. (4.8)
Условным математическим ожиданием одной из случайных вели-
чин, входящих в систему (X,Y), называется её математическое ожидание,
вычисленное при условии, что другая величина приняла определённое значе-
ние
.
// / /
11
[/ ] , [/] .
j
ij i ji
nm
j
xy i x y i yx j y x
ij
MX y m xp MY x m yp
(4.9)
Условные математические ожидания
)(]
/
[ yyX
M
и ( [/ ]
j
M
Xy)
есть функции переменной y (или
i
y) и называются регрессией X на y, а
функции
]
/
[
x
Y
M
= )(ψ
x
и ]/[
i
xYM – регрессией Y на x.
Задача 4.1
Два стрелка независимо друг от друга сделают по два выстрела в одну
и ту же мишень. Вероятность попадания для первого стрелка равна 0,8, для
второго – 0,6. Пусть
Х – число попаданий первого стрелка, Y – второго.
Найти:
a) совместное распределение случайных величин
Х и Y;
б) одномерные законы распределения случайных величин
Х и Y;
в) вероятность события
A =
1, 0 ;XY
г) зависимы или нет случайные величины Х и Y.
Решение задачи
По условию задачи стрелки стреляют независимо друг от друга, сле-
довательно, случайные величины
Х и Y независимы. Удобно в этом случае
сначала найти одномерные законы распределения случайных величин
Х и
54
Y. Обе рассматриваемые случайные величины имеют биномиальное распре-
деление и могу принимать значения 0, 1, 2 (
n = 2, p = 0,8 или 0,6).
Согласно формуле Бернулли (1.3) сформированы ряд распределения
случайной величины
Х, представленный в табл. 4.1, и ряд распределения
случайной величины
Y, представленный в табл. 4.2. Условия нормировки
выполняются в обоих случаях.
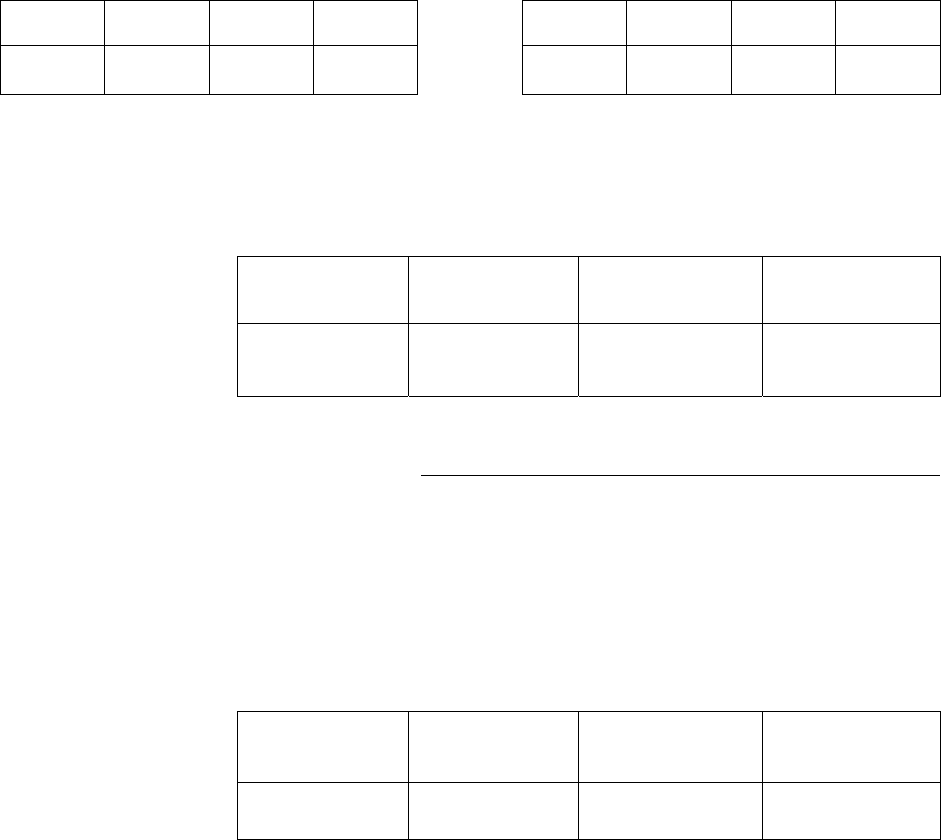
Таблица 4.1 Таблица 4.2
i
x
0 1 2
j
y
0 1 2
i
x
p
0.04 0.32 0.64
j
y
p
0.16 0.48 0.36
Поскольку случайные величины Х и Y независимы, то их совместные
вероятности вычисляются по формуле (4.4) и образуют двумерную матрицу
(табл. 4.3).
Таблица 4.3
x
i
/ y
j
0
1
2
0 0,0064 0,0192 0,0144
1 0,0512 0,1536 0,1152
2 0,1024 0,3072 0,2304
Вероятность события
A =
1, 0 ;XY
равна сумме вероятностей
1,1 1, 2
( ) 0,1536 0,1152 0, 2688PA p p
.
Случайные величины Х и Y независимы.
Задача 4.2
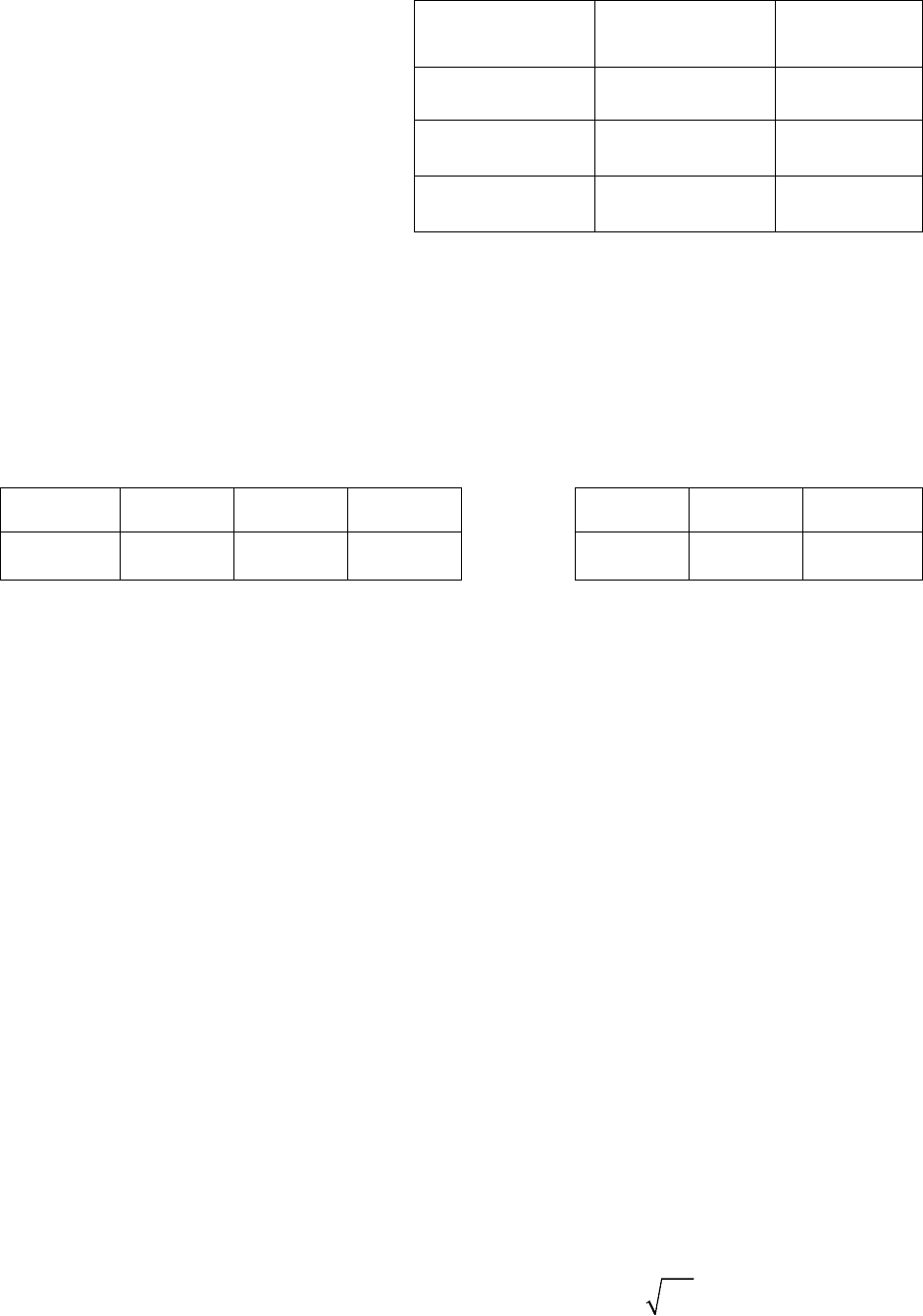
Таблица 4.4
55
Задана матрица распреде-
ления двумерной случайной ве-
личины (
Х, Y) (табл. 4.4).
Определить:
а) законы распределения
составляющих
Х и Y;
б) являются ли
Х и Y не-
зависимыми случайными вели-
чинами;
в)
числовые характеристики двумерной случайной величины;
г) условные законы распределения;
д) функции регрессии.
Решение задачи
а) Законы распределения составляющих Х и Y представлены их
рядами распределений (табл. 4.5, 4.6). Вероятности
i
x
p и
j
y
p
вычисляют-
ся в соответствии с формулами (4.3) и (4.4).
11
1, 2,3
1, 2
;
ij
mn
x
ij y ij
ji
i
j
p
pp p
. 3, 2nm
.
Условия нормировки выполняются:
32
11
1; 1
ij
xy
ij
pp
.
б)
Случайные величины Х и Y, входящие в систему, зависимы, по-
скольку не выполняется условие (4.4). Например, при
21
1, 2
2, 1, 0,18; 0,29; 0,4
xy
ijp p p , но 0, 29 0, 4 0,18
, следователь-
но,
Х и Y – зависимые случайные величины.
в)
Числовые характеристики:
3
1
[ ] 40 0,22 50 0,29 60 0,49 52,7
i
xix
i
mMX xp
.
2
1
[ ] 150 0,4 160 0,6 156
у jyj
j
mMY yp
.
3
22 2
2
1
[ ] 63,74; 7,98
i
xxixxõx
i
DDX m xp m D
.
i
x
/
j
y
150
160
40 0,12 0,10
50 0,18 0,11
60 0,10 0,39
Таблица 4.5 Таблица 4.6
i
x
40 50 60
j
y
150 160
i
x
p
0,22 0,29 0,49
j
y
p
0,40 0,60
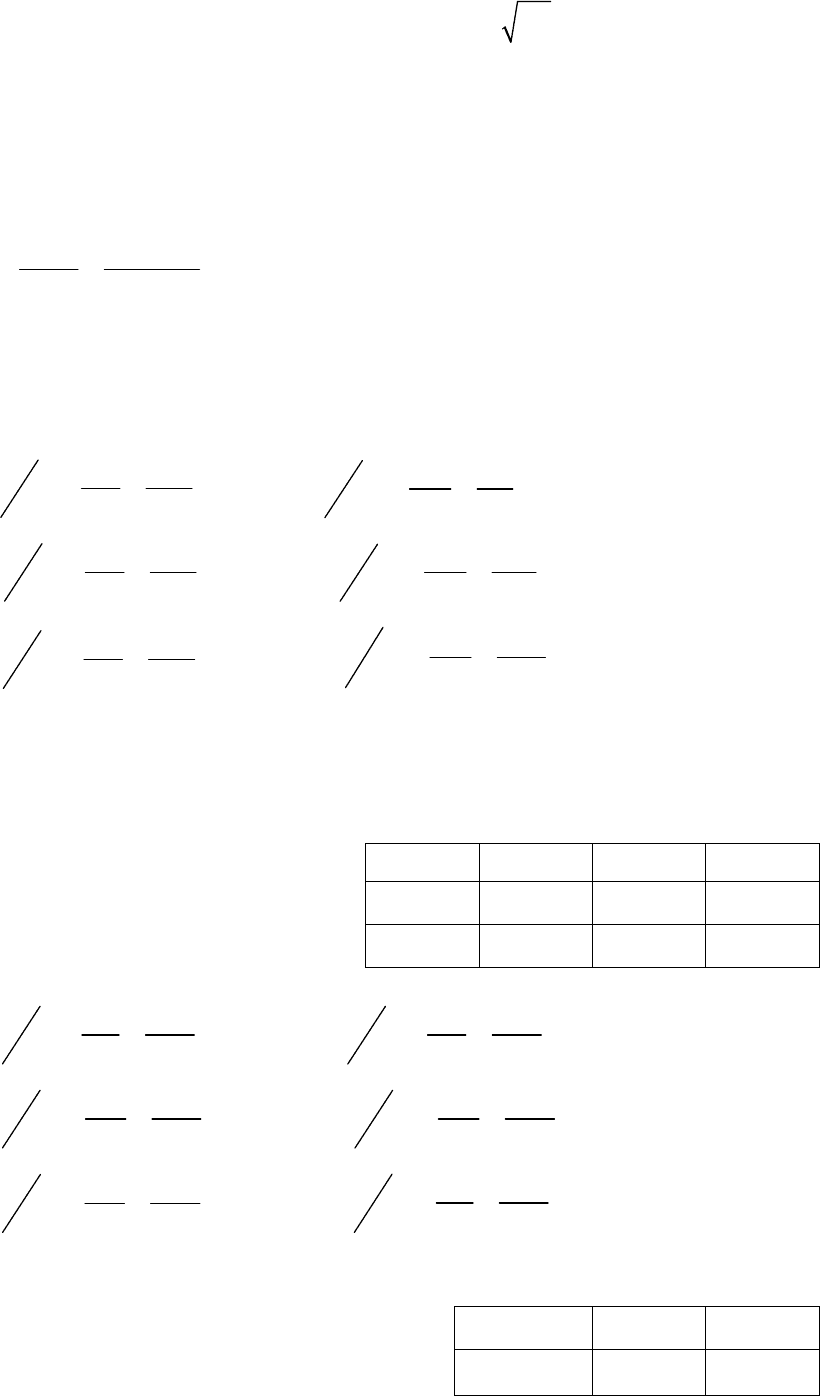
56
2
22 2
2
1
[] 24; 4,9
j
yyiyyyy
j
DDY m yp m D
.
Согласно формулам (4.6) вычисляются значения корреляционного
момента и коэффициента корреляции:
32
11
[( )( )]
x
yxyijijxy
ij
KMXmYm xypmm
13.
13
0,32
7,98 4,9
xy
xy
xy
K
r
.
г)
Условные законы распределения
Условные вероятности того, что случайная величина
X примет задан-
ное значение
x
i
, при условии что Y = y
j
, определяется равенствами (4.8):
1
11
1
1
0,12
0,3;
0, 4
y
p
x
P
y
p
2
12
1
2
0,1
0,17;
0,6
y
p
x
P
y
p
1
21
2
1
0,18
0, 45;
0, 4
y
p
x
P
y
p
2
22
2
2
0,11
0,18;
0,6
y
p
x
P
y
p
1
31
3
1
0,10
0, 25
0, 4
y
p
x
P
y
p
.
2
32
3
2
0,39
0, 65
0, 6
y
p
x
P
y
p
.
В табл. 4.7 представлена матрица условных распределений случайной
величины
X, когда случайная величина Y принимает два значения
y
1
= 150 и y
2
= 160.
Нетрудно заметить, что усло-
вия нормировки выполняются, т. е.
3
1
1
(/)1
i
i
Px y
,
3
2
1
(/ )1
i
i
Px y
.
1
11
1
1
0,12
0,55;
0, 22
x
p
y
P
x
p
1
12
2
1
0,10
0, 45;
0, 22
x
p
y
P
x
p
2
21
1
2
0,18
0,62;
0, 29
x
p
y
P
x
p
2
22
2
2
0,11
0,38;
0, 29
x
p
y
P
x
p
3
31
1
3
0,1
0, 20;
0, 49
x
p
y
P
x
p
32
2
3
3
0,39
0,80
0, 49
x
P
y
P
x
P
.
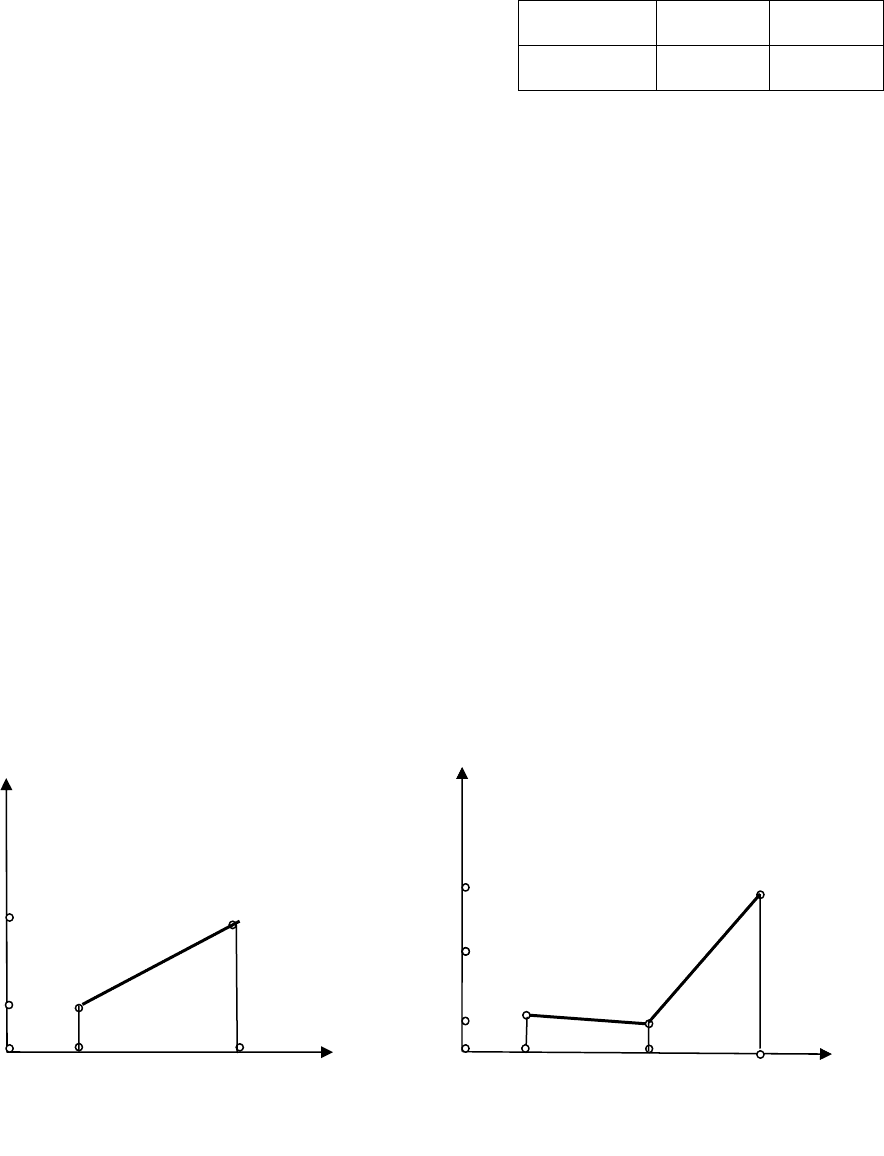
Таблица 4.7
x
i
40 50 60
P(x
i
/y
1
) 0,30 0,45 0,25
P(x
i
/y
2
) 0,17 0,18 0,65
Таблица 4.8
y
j
150 160
1
(/)
j
Py x
0,55 0,45
57
В табл. 4.8 представлена матрица
условных распределений случайной величи-
ны
Y, когда случайная величина X прини-
мает значения
x
1
= 40, x
2
= 50, x
3
= 60.
Условия нормировки выполняются.
д) Условные математические ожидания:
n
i
ii
yxpxyXM
1
11
;5,4925,06045,0503,040)/(]/[
3
1
22
;8,5465,06018,05017,040)/(]/[
i
ii
yxpxyXM
m
j
jj
xypyxYM
1
11
;5,15445,06055,0150)/(]/[
m
j
jj
xypyxYM
1
22
;8,153385,016062,0150)/(]/[
33
1
[ / ] ( / ) 150 0,2 160 0,80 158.
m
jj
j
MY x y py x
На рис. 4.1 и 4.2 изображены функции регрессией
X на y
()(]
/
[ yyX
M
) и Y на x (]
/
[
x
Y
M
= )(ψ
x
) соответственно.
4.2. Система непрерывных случайных величин
Плотностью распределения ),( y
x
f
(совместной плотностью рас-
пределения
) для системы двух непрерывных случайных величин называется
вторая смешанная производная её функции распределения
2
(/)
j
Py x
0,62 0,38
3
(/)
j
Py x
0.20 0,80
150
160
/
x
y
m
/yx
m
y
158
154
156
50
40
60
Рис. 4.1
Рис. 4.2
x
55
50

58
yx
F
yxf
2
),( . (4.10)
Совместная функция распределения
x
y
dydxyxfyxF . ),(),(
(4.11)
Условие нормировки
1 ),( dydxyxf. (4.12)
Одномерные плотности распределения составляющих X и Y
.),()( ,),()(
21
dxyxf
dy
dF
yfdyyxf
dx
dF
xf (4.13)
Условия независимости двух непрерывных случайных величин, со-
ставляющих систему
),(
Y
X,
)()(),(
21
yfxfyxf .
Совместная плотность распределения зависимых случайных ве-
личин
yxfyfxyfxfyxf /)(/)(),(
1221
. (4.14)
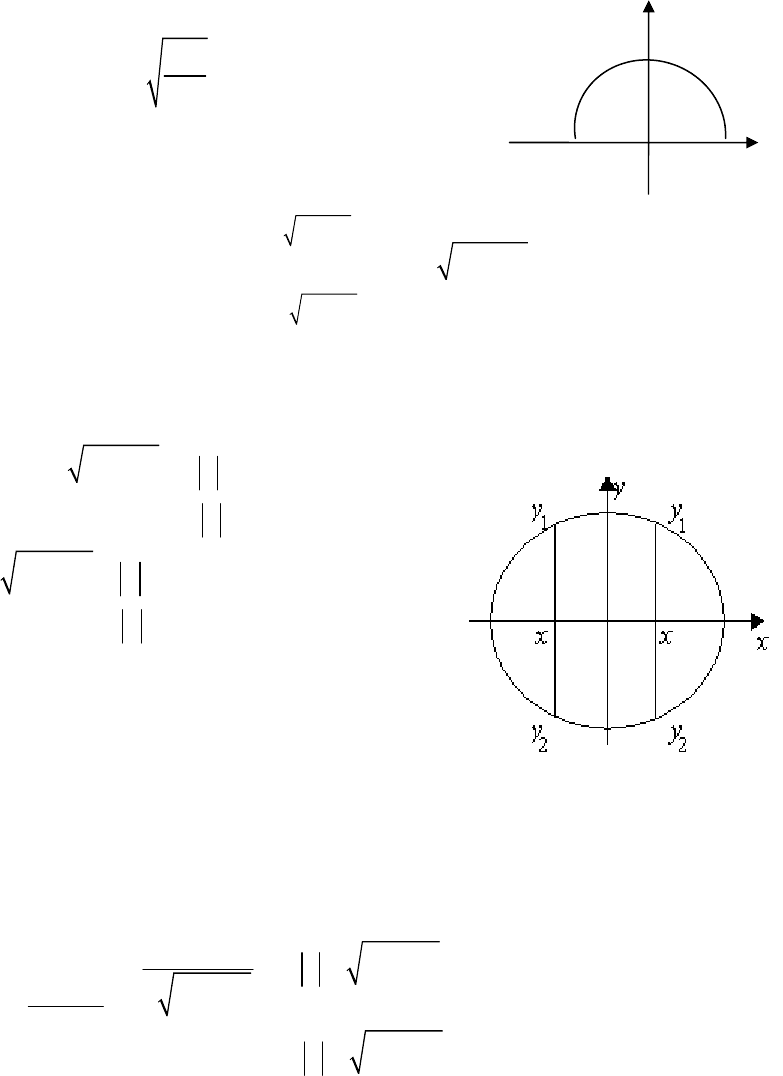
Задача 4.3
Поверхность распределения f(x,y)
системы случайных величин (
X,Y) пред-
ставляет прямой круговой цилиндр, центр
основания которого совпадает с началом
координат, а высота равна
h (рис. 4.3).
Определить:
а) радиус цилиндра
r;
б) законы распределения составля-
ющих
f
1
(x) и f
2
(x);
в)
являются ли случайные величины
Х и У независимыми;
г) условные законы распределения;
д) числовые характеристики.
Решение задачи
Рис. 4.3
h
59
Итак, система случайных величин (X,Y) имеет равномерное распреде-
ление внутри окружности радиуса
r. Совместная плотность распределения
имеет вид
222
222
, ,
(, )
0, .
hxyr
fxy
x
yr
а) Из условия нормировки для совместной
плотности распределения объем цилиндра дол-
жен быть равен единице.
2
1
1 rh r
r
.
б) Согласно формуле (4.13) определяются
одномерные плотности распределения со-
ставляющих X и Y:
22
1
22
2
22
1
() (, ) 2
y
rx
y
rx
f
x f x y dy h dy h dy h r x
.
Пределы интегрирования y
1
и y
2
находятся с помощью рис. 4.4.
Таким образом,
22
1
2, ,
()
0, .
hr x x r
fx
x
r
22
2
2, ,
()
0, .
hr y y r
fx
yr
в) Условие независимости случайных
величин Х и Y, входящих в систему (Х, Y) в
рассматриваемом случае не выполняется
(
12
(, ) () ()
f
xy f x f y), следовательно, слу-
чайные
величины Х и Y, входящие в систему, зависимы.
г)
Условные законы распределения определяются согласно формуле
(4.14). На рис. 4.5 представлен график условной плотности
1
(/)
f
xy.
22
22
1
2
22
1
, ,
(, )
2
(/)
()
0, .
x
ry
fxy
ry
fxy
fy
x
ry
Рис. 4.4
x
1
(/)
f
xy
r
r
Рис. 4.5
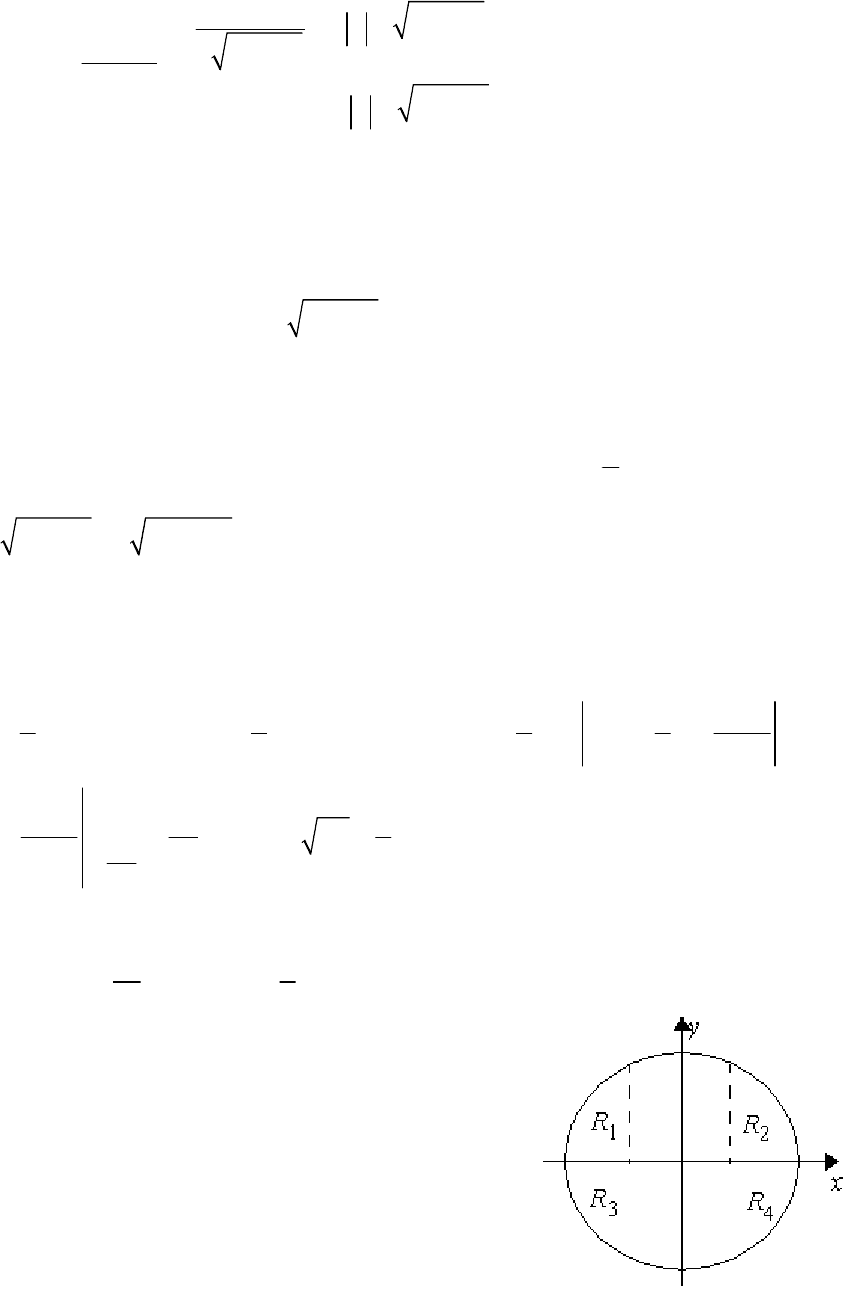
60
22
22
2
1
22
1
, ,
(, )
2
(/)
()
0, .
yrx
fxy
rx
fyx
fx
yrx
д)
Числовые характеристики
В силу симметрии совместной плотности
распределения 0
yx
mm .
2222
1
() 2
r
x
r
D
xfxdx h x r xdx
.
Переходя от декартовой к полярной системе координат, получим
sin , cos ; arcsin 1
2
xr t dxr tdtx r t
;
22 2
1sin cos ;rxr tr t
/2 /2
22 4 2 2
/2 /2
2 sin cos cos 2 sin cos
x
D h r t r t dt r t dt hr t t dt
/2 /2
/2 /2
/2 /2
42 4 4 2
/2 /2
11 11sin4
sin 2 (1 cos 4 )
24 444
t
hr t dt hr t dt hr t hr
;
44
24
2
1
rhr
r
h
2
xx
r
D
.
Аналогично вычисляется дисперсия
y
D
.
2
;
42
xy xy
rr
DD
.
Суммарный корреляционный момент равен нулю. Действительно, в
соответствии с рис. 4.6 в двух ближайших квадрантах
12
,
R
R и
3 4
,
R
R каж-
дому заданному значению координаты y соответствуют два равных, но
имеющих противоположные знаки, значения координаты x. Следовательно,
два соседних интеграла взаимно уничтожаются.
(, )
xy
R
K
xy f x y dx dy
1234
0
RRRR
h xydxdy xydxdy xydxdy xydxdy
.
Случайные величины Х и Y зависимы, но некоррелированы.
Рис. 4.6
Рис. 4.5
