Самусевич Г.А. Теория вероятностей в примерах и задачах. Теория вероятностей и математическая статистика
Подождите немного. Документ загружается.


61
Условные математические ожидания равны нулю.
22
22
22
22
2
1
22 22
1 1
0
22
2
ry
ry
ry
x
y
ry
xdx x
xx
mM xf dx
yy
ry ry
.
Таким образом,
.0
x
y
y
x
mm
4.3. Двумерное нормальное распределение
k
B
– эллипс рассеяния, оси симметрии которого параллельны осям
координат, а полуоси
yx
aa , пропорциональны среднеквадратическим от-
клонениям
x
σ
и
y
σ , т.е.
x
x
ka
,
yy
ka σ
. Уравнение эллипса В
k
име-
ет вид
2
2
2
2
2
σσ
)(
)(
k
my
mx
y
y
x
x
, (4.15)
а вероятность попадания в него случайной точки (X,Y)
2
2
1}),{(
k
k
eBYXP
. (4.16)
Вероятность попадания случайной точки (X,Y) в прямоугольник R
со сторонами, параллельными осям эллипса рассеяния (в этих условиях слу-
чайные величины X и Y независимы),
{( , ) }
δγ
σσ
yy
xx
xx yy
mm
mm
PXY R
. (4.17)
Задача 4.4
Случайная величина (Х,Y) распределена по нормальному закону на
плоскости с параметрами:
1; 1; σ 1; σ 2; 0.
xy xyxy
mm r
Найти ве-
роятность того, что случайная точка попадет внутрь области D, ограничен-
ной эллипсом:
.1
4
)1(
2
)1(
2
2
2
2
yx
Решение задачи.
Приведенное уравнение эллипса показывает, что его оси параллельны
координатным осям (отсутствуют смешанные произведения в записи урав-
нения эллипса), а его полуоси равны a = 2, b = 4. Учитывая приведённые
значения
σ
x
и σ
y
, коэффициент k в формулах (4.15) и (4.16) следует при-
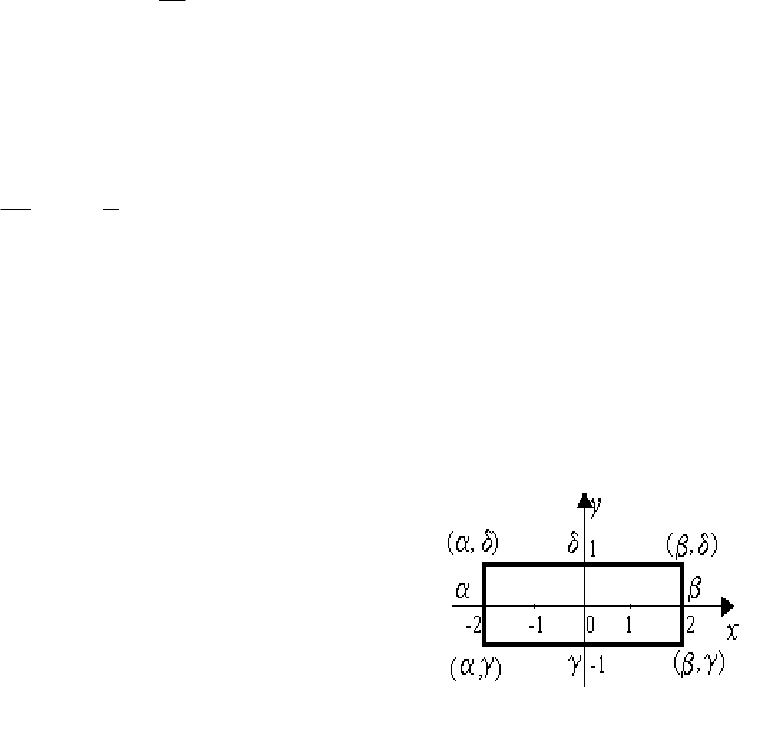
62
нять равным двум. σ 2; σ 4 2.
xy
ak bk k Тогда в соответствии с
формулой (4.16) получим
2
2
2
{( , ) } 1 1 0,875
k
k
PXY B e e
.
Задача 4.5
Случайная точка (Х,Y) распределена на плоскости по нормальному за-
кону
22
11
(, ) exp ( ).
22
fxy x y
Найти вероятность попадания точки (Х,Y) в прямоугольник R со сто-
ронами, равными 2 и 4 и с центром в начале координат (рис. 4.7).
Решение задачи.
Судя по формуле приведенной совместной плотности, нормальное
распределение некоррелировано, имеет нулевые математические ожидания
и единичные дисперсии. Стороны прямо-
угольника R параллельны осям координат.
2, 2, 1, 1
. Применяя фор-
мулу (4.17) и используя прил. 2 получим
{( , ) } 2 2 1 1 2 (2) 2 (1) 0,3413 0,4772 0,163.PXY R
5. Функции случайных величин
5.1. Функции одного дискретного случайного аргумента
[1, разд. 5.1, с 83 -84]
Задана функция ()YX и ряд распределения дискретной случайной
величины X. Требуется построить ряд распределения случайной величины
Y. Это осуществляется в два этапа:
а) сначала строится
неупорядоченный ряд. Для каждого значе-
ния аргумента
i
x
вычисляется значение функции
)(φ
ii
xy
, i = 1, 2 ,… , n.
iiii
pxXPxYPyYP
; (5.1)
в) для формирования
ряда распределения Y (упорядоченного ря-
да
) необходимо все значения )(φ
i
x расположить в порядке возрастания,
сопоставив их с вероятностями
i
p. Если среди значений )(φ
i
x есть оди-
Рис. 4.7
63
наковые, например
)(φ
k
x
=
)(φ
l
x
, то в числе значений
j
y они записывают-
ся один раз и этому значению соответствует
суммарная вероятность.
j
kkl
p
PY x p p . (5.2)
Задача 5.1
Случайная величина X задана рядом распределения. Найти закон
распределения случайной величины
23YX
( () 2 3
iii
yxx
).
Ряд распределения случайной величины
X
x
i
0 1 2 3 4 5
p
i
0,14 0,27 0,27 0,18 0,09 0,04
Неупорядоченный ряд распределения случайной величины Y
(x
i
)
3 1 1 3 5 7
p
i
0,14 0,27 0,27 0,18 0,09 0,04
Упорядоченный ряд распределения случайной величины Y
y
j
1 3 5 7
Pj
0,54 0,32 0,09 0,04
Задача 5.2
Случайная величина
X
задана рядом распределения. Найти закон
распределения случайной величины
sinYX
(()sin
ii i
yx x
).
Ряд распределения случайной величины
X
x
i
0
/4 /2 3
/4
p
i
0,2 0,1 0,3 0,1 0,3
Неупорядоченный ряд распределения случайной величины Y
Упорядоченный ряд распределения случайной величины Y
(x
i
)
0
2/2
1
2/2
0
p
i
0,2 0,1 0,3 0,1 0,3
y
j
0
2/2
1
p
j
0,5 0,2 0,3
64
5.2. Функция одного непрерывного случайного аргумента
[1, разд. 5.4, с 88 - 91]
Задана функция )(
X
Y
. Требуется найти её плотность распре-
деления
)( y
g
. )( y
x
, )( y
– функция, обратная функции )(
x
y
.
Плотность распределения монотонной функции одного случайного
аргумента.
() [ ()] ().gy f y y
(5.3)
Плотность распределения немонотонной функции одного случайного
аргумента
)()]([)(
1
yyfyg
j
k
j
j
. (5.4)
Задача 5.1
Случайная величина
X
задана плотностью распределения
)(
x
f
на
интервале (, )ab. Найти плотность распределения )(y
g
случайной величи-
ны .3
X
Y
Функция () 3yxx монотонна, следовательно, справедлива фор-
мула (5.3). Обратная функция
1
() ; .
33
y
xy
Таким образом,
1
( ) ( ) , , 3 3 .
3
gy f y a x b a y b
Задача 5.2
Случайная величина
X
задана плотностью распределения )(
x
f
на ин-
тервале
(0, ).
x
Найти плотность распределения
)(yg
случайной вели-
чины Y для трех вариантов зависимости
().YX
Решение задачи
Вариант 1.
X
Ye
.
1
( ) ; ln ; ( ) ln
x
yxe xyx y
y
;
2
11 1
()
1/
y
yy
y
.
0 1; 0.
x
yx y
Функция
x
ye
монотонна на интервале (0, )
x
, в соответствии
с формулой (5.3) имеем
11
() ln , 0 1.gy f y
yy
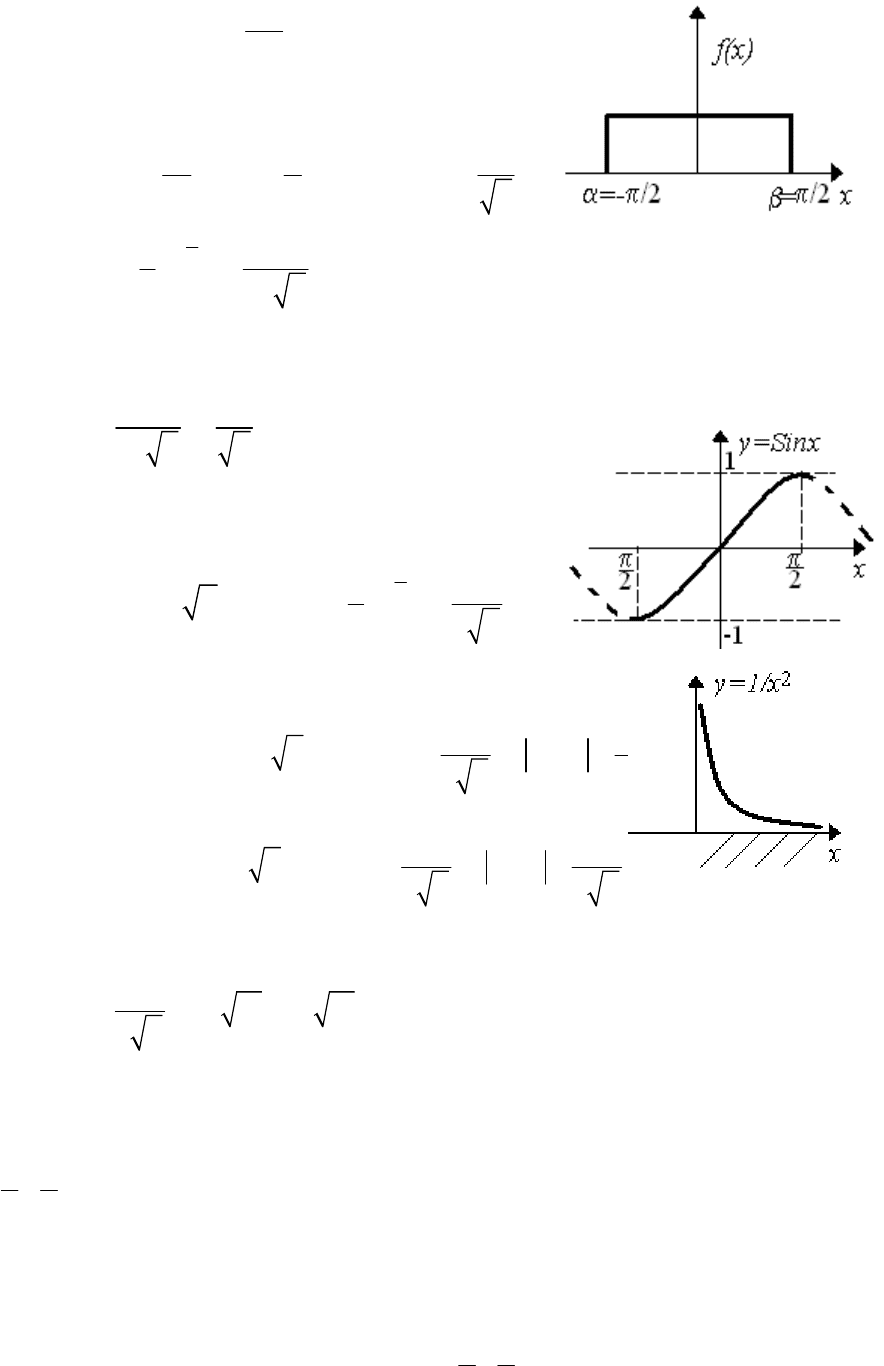
65
Вариант 2.
2
1
Y
X
.
Как показано на рис. 5.1 функция
()yx
монотонна на интервале (0, )
x
.
2
2
11 1
( ) ; ; ( )yx x x y
y
y
x
;
3
2
11
()
2
2
yy
yy
.
0 ; 0.
x
yxy
В соответствии с формулой (5.3) имеем
11
( ) , 0 .
2
gy f y
yy y
Вариант 3.
22
, ; ( ) ;YX x y x x
() ;
x
yy
1
2
11
()
2
2
yy
y
.
Функция ()yx имеет два участка мо-
нотонности.
11
0, ( ) ; ( ) , ( )
22
xxyx x
yy
.
11
0 , ( ) ; ( ) , ( )
22
xxyx x
yy
.
В соответствии с формулой (5.4) имеем
1
( ) ( ) ( ) , 0 .
2
gy f y f y y
y
Задача 5.3
Случайная величина
X
распределена равномерно на интервале
;
22
(рис. 5.2). Найти плотность распределения
)(y
g
случайной вели-
чины .sinX
Y
Решение задачи
Функция
() sinyx x
на интервале
;
22
монотонна (рис. 5.3).
Рис. 5.3
Рис. 5.2
Рис. 5.1

66
11
()fx
.
1
, ; ,
22
()
0, ; .
22
x
fx
x
( ) arcsin .
x
yy
2
1
()
1
y
y
.
Таким образом,
2
11
, 1; 1 ,
()
1
0, 1; 1 .
y
gy
y
y
Задача 5.4
Случайная величина
X
распределена равномерно на интервале
0; 2π . Найти плотность распределения
)(yg
случайной величины .cos
X
Y
1
, 0; 2 ,
2
()
0, 0; 2 .
x
fx
x
Как показано на рис. 5.4 функция y на ин-
тервале
0; 2 имеет два участка монотонно-
сти:
11
2
1
(0; ), ( ) arccos ,
1
xyy
y
;
22
2
1
( ; 2 ), ( ) arccos ,
1
xyy
y
.
В соответствии с формулой (5.4) определяет-
ся плотность распределения случайной величи-
ны Y:
222
11 11 1
()
22
111
gy
yyy
.
Таким образом,
Рис. 5.5
arccos
x
y
Рис. 5.4

67
2
11
, 1; 1 ,
()
1
0, 1; 1 .
y
gy
y
y
Контроль выполнения условия нормировки: .1)(
dyyg
1
1
1
2
1
11 1 1
arcsin 1.
1
dy y
y
5.3. Композиция законов распределения
[1, разд. 5.4.2, с 91 - 93]
Если случайные величины Х и Y
независимы, то закон распределения
их
суммы Z=X+Y называется композицией законов распределения.
В случае, когда Х и Y непрерывные случайные величины, композиция
приводит к
свертке суммируемых законов распределения.
dyyfyzfdxxzfxfzg )()()()()(
2121
. (5.5)
Задача 5.5
Заданы законы распределения независимых случайных величин Х и Y.
Найти закон распределения их суммы Z=X+Y.
Ряд распределения случайной величины X
x
i
10 12 16
i
x
p
0,4 0,1 0,5
Ряд распределения случайной величины Y
y
j
6 10
j
y
p
0,2 0,8
Поскольку случайная величина Z есть сумма Z=X+Y, то она прини-
мает все возможные значения, равные
ki j
zxy
, для всех индексов i и j
(i = 1, 2, 3; j = 1, 2). Вероятности этих значений равны
{}{ ; }{ }{ } ,
ij
kijijxy
Pzz PXxYy PXxPYy p p
68
По полученным данным сначала формируется неупорядоченный ряд
распределения случайной величины Z
k
z
16 20 18 22 22 26
p
0,08 0,32 0,02 0,08 0,1 0,4
а затем и упорядоченный ряд
z
k
16 20 18 22 26
k
z
p
0,08 0,02 0,32 0,18 0,4
Задача 5.6
Заданы законы распределения независимых случайных величин Х и
Y. Найти композицию этих законов.
Решение задачи
Случайные величины Х и Y имеют показательное распределение с
параметрами λ
x
= 1/3 и λ
y
= 1/5.
3
1
1
, 0,
()
3
0, 0.
x
ex
fx
x
5
2
1
, 0,
()
5
0, 0.
y
ey
fy
y
Случайная величина Z – их сумма Z=X+Y,
следовательно, z = x+y. Согласно формуле (5.5)
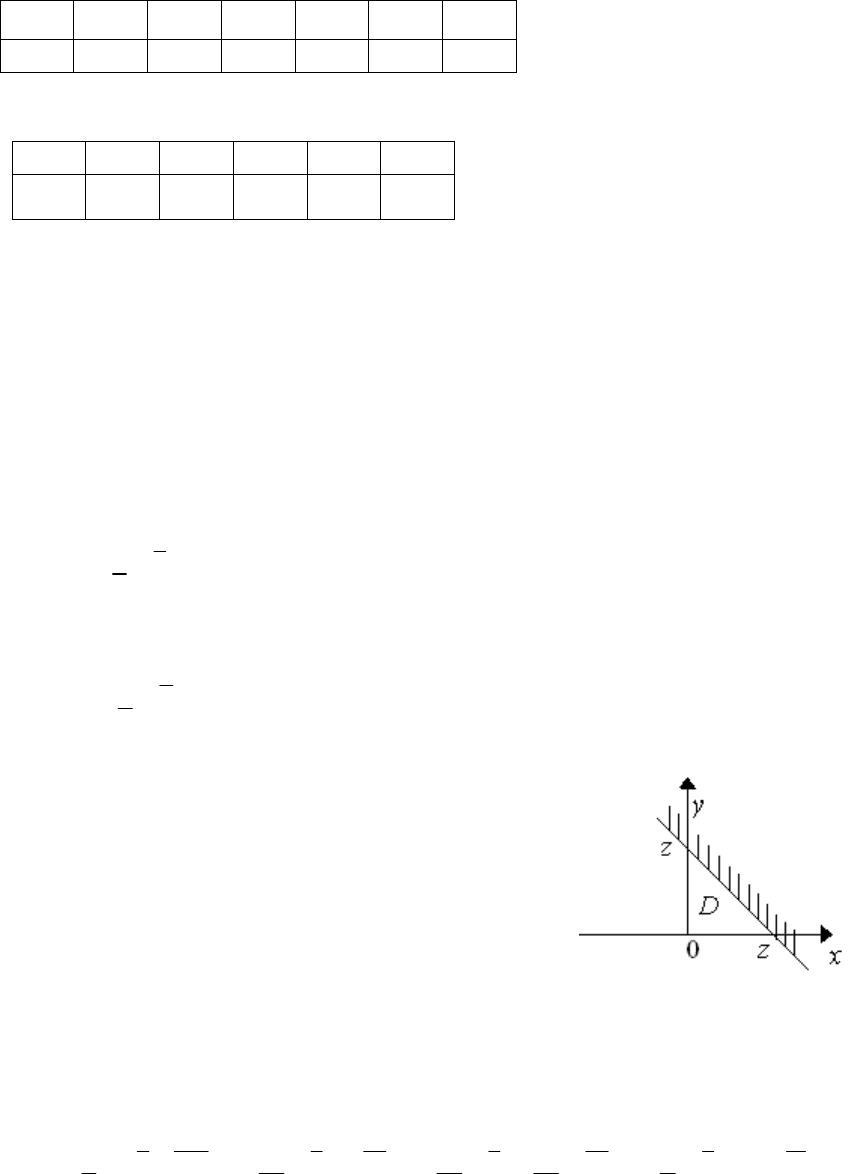
интегрирование производится по области D. В
рассматриваемом случае это область положитель-
ных переменных x и y, границей которой (для
заданного z) служит прямая x+y = z (рис. 5.6).
Таким образом,
12
() () ( )
D
gz f xf z xdx
=
12
0
() ( )
z
f
xf z xdx
.
222
35 5 15 5 15 5 15
00
0
111151
() 1
5151522
z
xzxzxzxz
zz
z
g z e e dx e e dx e e e e
.
Таким образом
Рис. 5.6

69
2
515
1
1 , 0,
()
2
0, 0.
z
z
ee z
gz
z
Задача 5.7
Найти композицию нормальных законов.
2
2
1
1
() ;
2
x
fx e
2
2
2
1
()
2
y
fy e
.
Найти композицию в рассматриваемой задаче – это значит найти за-
кон распределения суммы
Z
XY
независимых, нормально распреде-
лённых случайных величин Х и Y с параметрами
0; σσ1
xy xy
mm
.
Применяя теоремы о числовых характеристиках, имеем
0;
zxy
mmm 2; σ 2
zxy z
DDD .
Подставляя функции
1, 2
() ()
f
xfy в интеграл свертки (5.5), преоб-
разуем показатель степени подынтегрального выражения так, чтобы произ-
вести замену переменных
22
()
22
12
11
() () ( ) ;
22
xzx
A
gz f xf z xdx e e dx edx
2
22 2
22
11
22(2) 2 ;
22222
22
zz z z z
Axx z x
.
2
;2 ;
2
2
dt
dxdxdt
z
xt
Итак,
22
42
1
()
22
zt
gz e e dt
.
Интеграл Эйлера – Пуассона
2
2
t
edt
равен 2 . Тогда функция
g(z) преобразуется к виду, доказывающему, что случайная величина Z
распределена нормально
2
2
2( 2)
1
( ) 0, 2.
22
z
zz
gz e m
Задача 5.8
70
Заданы законы распределения незави-
симых случайных величин Х и Y. Найти ком-
позицию этих законов.
1
1
, (2, 6),
()
4
0, (2, 6).
x
fx
x
2
1
, (1, 3),
()
2
0, (1, 3).
y
fy
y
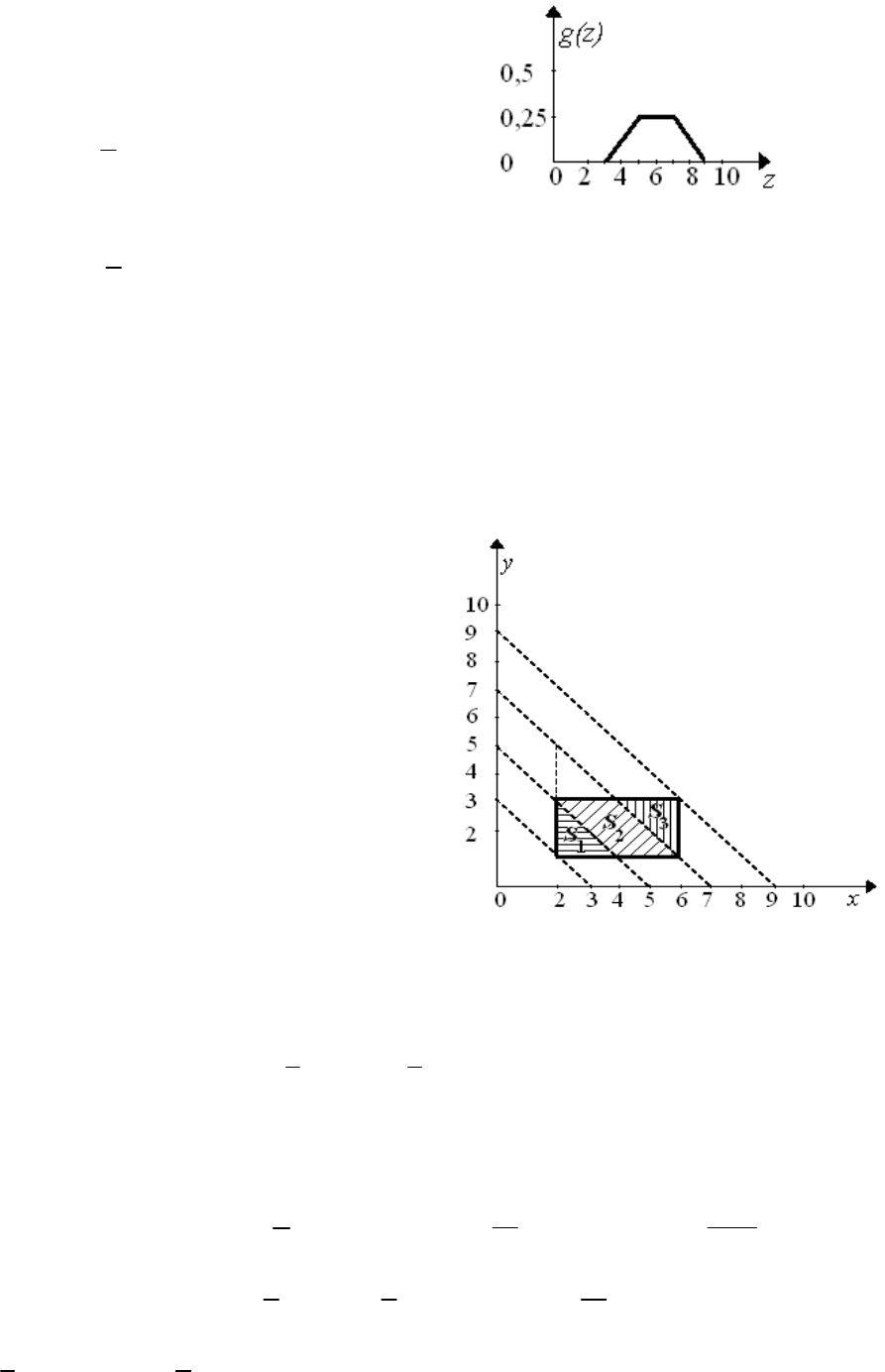
Решение задачи
Представлена система двух независимых равномерно распределенных
случайных величин внутри прямоугольника, изображенного на рис. 5.7.
Требуется найти закон распределения суммы этих величин Z=X+Y.
В рассматриваемом случае удобно
сначала найти функцию распределения
случайной величины Z
() { }Gz PX Y Z
Для этого требуется проинтегриро-
вать совместную плотность распределе-
ния по области S (прямоугольник на рис.
5.7). Плотность распределения случайной
величины Z находится дифференцирова-
нием функции
()Gz
.
Совместная плотность распределе-
ния независимых случайных величин в
области S равна
12
(, ) () () 1/8fxy f xf y.
12
11
() () () ()
88
SS
G z f x f y dx dy dx dy S z
.
Область S делится на подобласти прямыми линиями x+y = z для
двух значений z, z = 5, z = 7. Таким образом
2
1
35, S()(3),
2
zzz
2
13
() ( 3); () .
16 8
z
Gz z gz
22
11
57, ()(3)(5)
22
zSzz z
.
22
1
() ( 3) ( 5)
16
Gz z z
;
11
() 3 5 .
84
gz z z
Рис. 5.7
Рис. 5.8
