Самусевич Г.А. Теория вероятностей в примерах и задачах. Теория вероятностей и математическая статистика
Подождите немного. Документ загружается.


41
если известно, что вероятность того, что за это время откажет хотя бы один
элемент, равна 0,98.
Решение задачи
Ситуация в рассматриваемой задаче соответствует ситуации в преды-
дущей задаче, т.е. случайная величина
X (число отказавших элементов в
течение времени
Т) имеет биномиальное распределение. Но поскольку
устройство состоит из большого числа работающих элементов с одинако-
вой, очень маленькой вероятностью отказа каждого элемента за время
Т, то
биномиальное распределение можно заменить распределением Пуассона.
Среднее число отказавших за время
Т элементов есть математическое ожи-
дание, равное для распределения Пуассона значению его параметра
a.
Событие
A = {за время Т откажет хотя бы один элемент (m > 0)},
противоположное событие
A
= {не откажет ни один элемент (m = 0)}. Ис-
пользуя формулу (2.10), получим
;98,011)(
0
a
ePAP
;02,0
а
е
ln 0,02a
.
m
x
= .91,350ln a
Задача 3.4
Радиостанция излучает сигнал в течение 10 мкс. Работа происходит в
условиях действия хаотической импульсной помехи, среднее число импуль-
сов которой в одну секунду составляет 10
4
. Для срыва передачи достаточно
попадания одного импульса в период работы станции. Считая, что число
импульсов помехи, попадающих в заданный интервал, распределено по за-
кону Пуассона, найти вероятность срыва передачи.
Решение задачи
541
10 мкс 10 ; 10 ; 0,1ccа
.
Случайная величина
X – число импульсов, попавших на заданный
интервал (период работы станции). Для срыва передачи достаточно попада-
ния хотя бы одного импульса в этот период.
};0{1}1{ XPXP
0,1
{0} 0,905;
a
PX e e
.095,0905,01}1{ XP
Задача 3.5
Среднее число отказов радиоаппаратуры за 10 000 часов работы равно
10. Определить вероятность отказа радиоаппаратуры за 100 часов работы.
Решение задачи
Событие А = {хотя бы один отказ за 100 часов};

42
Отказы аппаратуры образуют простейший поток событий. Среднее
число отказов радиоаппаратуры есть математическое ожидание, равное для
распределения Пуассона значению его параметра
a = λτ. λ – интенсив-
ность простейшего потока событий, τ – значение интервала времени.
1
10000 ч ;
3
11111
10; ; / 10 отк/ч
x
ma а a
.
3
222
100 ч; 10 100 0,1а
.
0,1
() 1 { 0}1 0,095.PA РХ е
Задача 3.6
Вероятность того, что в течение часа любой абонент позвонит на
коммутатор, равна 0,01. Телефонная станция обслуживает 300 абонентов.
Найти вероятность того, что в течение часа позвонят 4 абонента.
Решение задачи
Случайная величина X – число абонентов, позвонивших в течение ча-
са, имеет биномиальное распределение с параметрами
n = 300, p = 0,01 или
предельное распределение Пуассона с параметром
a = np = 3, m = 4.
4
3
3
( ) 0,169.
!4!
m
a
m
a
PA P e e
m
Задача 3.7
В течение часа коммутатор получает в среднем 60 вызовов. Какова
вероятность того, что за тридцать секунд, в течение которых телефонистка
отключалась, не будет ни одного вызова.
Решение задачи
Вызова, поступающие на коммутатор, образуют простейший поток
событий с интенсивностью 60 выз/ч 1 выз/мин
. Случайная величина
X – число вызовов, поступивших за время 30 0,5 минc
, имеет распре-
деление Пуассона с параметром 0,5
а
.
0,5
0
( ) { 0} 0,606.PA PX P e
Задача 3.8
При работе ЭВМ возникают сбои. Поток сбоев можно считать про-
стейшим, среднее число сбоев за сутки равно 1,5. Найти вероятность того,
что:
а) за двое суток не произойдет ни одного сбоя;
б) в течение суток произойдет хотя бы один сбой;
в) за неделю работы ЭВМ произойдет не менее трех сбоев.
Решение задачи
а)
11
сбоев
2 сут; 1,5 ; 3
сут
а
.
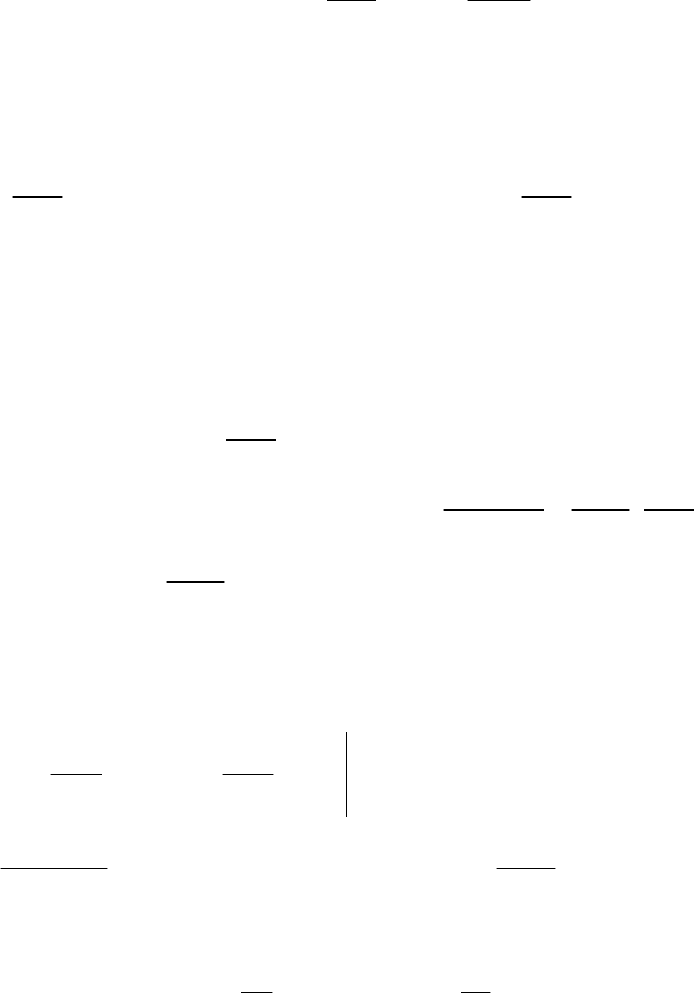
43
;05,0}0{)(
3
1
eeXPAP
a
b)
22
1 сут; 1,5а
.
;777,0223,011}0{1}1{)(
5,1
eXPXPВP
c)
33
7 сут; 10,5а .
2
2
10,5 10,5
0
10,5 10,5
( ) { 3} 1 1 ( ) 0,998.
1! 2!
i
i
P С PX P e e
Задача 3.10
Поток вызовов на АТС – пуассоновский нестационарный с интенсив-
ностью
λ()tbtc
на участке от 0 ч до 6 ч 40 мин. В момент времени
0
выз
0 (0) 0,2
мин
t , при
выз
6 ч 40 мин, ( ) 0,4
мин
kk
tt. Требуется
найти вероятность того, что в течение 10 мин от 3 ч 15 мин до 3 ч 25 мин
поступит не менее трех вызовов.
Решение задачи
Для определения постоянных b и c составляются два уравнения:
0
выз
1. 0, 0 0,2 0,2
мин
tbc с .
0, 4 0, 2 1 выз
2. 6 ч 40 мин 400 мин, 400 0,4;
400 2000 мин
k
tbcb
.
Таким образом,
() 0,2.
2000
t
t
Параметр
a распределения Пуассона может быть найден двумя спо-
собами:
1.
12
3 ч 15 мин 195 мин, 3 ч 25 мин 205 минtt
.
2
1
205
205
2
195
195
( ) 0, 2 ( 0, 2 ) 3
2000 4000
t
t
tt
а tdt dt t
.
2.
ср
ср ср ср ср
205 195
200 мин; ; 0,2 0,3
2 2000
t
t а
.
ср
0,3 10 3; 10 мин.а
22
3
3
( ) { 3} 1 (1 ) 1 (1 3 ) 0,575.
22
a
à
PA PX e à e
3.2. Показательное распределение
[1, разд. 3.3.4, с. 51 - 54]
Случайная величина X имеет показательное распределение, если ее
плотность распределения имеет вид

44
,0 ,
,0 ,0
)(
xe
x
xf
x
(3.4)
где
– параметр показательного распределения.
Функция распределения
.0 ,1
,0 ,0
)(
xe
x
xF
x
(3.5)
Числовые характеристики:
,
1
x
m
2
1
x
D
,
1
x
. (3.6)
Функцией надежности
)(
t
R
называется вероятность безотказной
работы
элемента за время длительности t, равная
.)(1)(
t
etFtR
(3.7)
Задача 3.11
Электронная лампа работает исправно в течение интервала времени
(0, T). T – случайная величина, распределенная по показательному закону
0, 0,
()
, 0.
t
t
ft
et
По истечении времени Т лампа выходит из строя и ее немедленно за-
меняют новой. Найти вероятность того, что за время :
а) лампу не придется менять (
надежность или вероятность безот-
казной работы за время
);
б) лампу придется заменить не более двух раз (2 и менее раз).
Решение задачи
Отказы ламп образуют простейший поток с интенсивностью λ. Слу-
чайная величина Х – число отказов за время , распределена по закону
Пуассона с параметром а = λτ.
а) A = {
ни одного отказа лампы за время
, m = 0}.
() { 0}
at
PA PX e e
;
б) B = {2 и менее отказа лампы за время , m = 0, 1, 2}.
22
2
0
()
() { 2} (1 ) 1 .
22
at
i
i
a
PB PX P e a e
Задача 3.12
45
Непрерывная случайная величина Х распределена по показательному
закону:
3
0, 0,
()
3, 0.
x
x
ft
ex
Найти вероятность того, что в результате испытания Х попадет в ин-
тервал (0,13; 0,7).
Решение задачи
0,13; 0,7; =3 .
()()()();PX fxdxF F
;1)(
3x
exF
.555,0122,0677,0}7,013,0{
13,037,03
еeXP
Задача 3.13
Длительность времени Т безотказной работы элемента имеет показа-
тельное распределение. Найти вероятность того, что за время длительности
1
50 чt элемент откажет. Интенсивность отказов 0,01 отк/ч.
Решение задачи
Случайная величина Т – это момент времени, в который происходит
отказ элемента. Функция распределения
() { } 1 , 0
t
Ft PT t e t
– вероятность отказа за время
t
.
Событие A = {отказ элемента произойдет раньше, чем наступит мо-
мент времени
1
t }.
.369,0111)(}{)(
5,05001,0
01,0
11
1
ееetFtТPAP
t
Задача 3.14
Испытываются два независимо работающих элемента. Длительность
времени безотказной работы их имеет показательное распределение. Ин-
тенсивность потока отказов для первого элемента равна 0,02 отк/ч, второго
– 0,05 отк/ч. Найти вероятность того, что за 6 ч:
а) оба элемента откажут;
б) оба элемента не откажут;
в) только один элемент откажет;
г) хотя бы один
элемент откажет.
Решение задачи
12
6 ч; 0,02 отк/ч; 0,05 отк/ч .
i
Т – длительность безотказной работы i - го элемента, i =1, 2;
46
i
q – вероятность отказа i - го элемента за время τ;
1
ii
p
q - надежность i - го элемента (вероятность безотказной ра-
боты за время τ);
1
0,02 6
11 1
{ } ( ) 1 1 1 0,887 0,113;qPT F e e
1
11 1
{ } 1 { } 0,887;pPT PT e
2
0,05 6
22 2
{ } ( ) 1 1 1 0,741 0,259;qPT F e e
;741,01
22
qp
;03,0259,0113,0)(
21
qqAP
;66,0741,0887,0)(
21
ppВP
;31,0113,0741,0259,0887,0)(
1221
qpqpCP
.34,066,011)(
21
ppDP
Задача 3.15
Производится испытание трех элементов, работающих независимо
один от другого. Длительности времени безотказной работы их распределе-
ны по показательному закону с параметрами:
12 3
0,1 отк/ч; 0,2 отк/ч; 0,3 отк/ч .
Найти вероятность того, что за 10 часов работы
откажут ( 10 ч ):
а) хотя бы один элемент;
б) не менее двух элементов.
Решение задачи
Случайная величина X – число отказавших элементов.
Надежности элементов (см. формулу (3.7)):
1
0,110
1
0,368;pe e
2
0,2 10
2
0,135;pe e
3
0,310
3
0,05pe e
.
Вероятности отказов:
;632,01
11
pq ;865,01
22
pq
33
1 0,995qp
.
123
( ) { 1} 1 { 0} 1 1 0,368 0,135 0,05 0,9975.PA PX PX ppp
123 123 123
123
(){2}1{2}1({0}{1})1(
) 1 (0,0025 0,0043 0, 0159 0,0494) 1 0,072 0,928.
PB PX PX PX PX ppp qpp pqp
ppq
3.3. Равномерное и нормальное распределения
[1, разд. 3.3.3, 3.3.5, с. 49 - 51, 54 – 58]
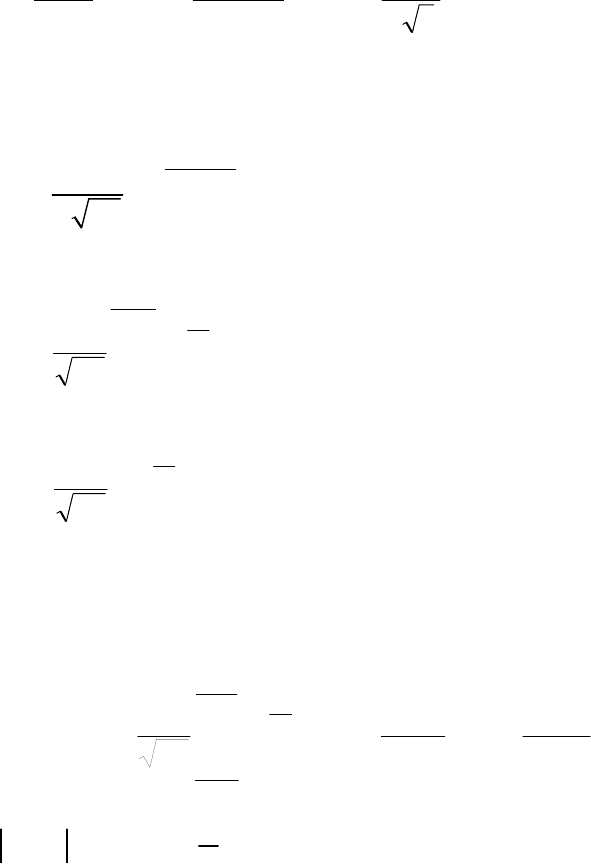
47
Случайная величина X имеет равномерное распределение на отрез-
ке [a, b], если ее
плотность распределения на этом отрезке постоянна.
.)( constc
x
f
Числовые характеристики равномерного распределения:
2
ba
m
x
,
12
)(
2
ab
D
x
,
32
ab
x
. (3.8)
Случайная величина X распределена по
нормальному закону с пара-
метрами т и σ, если ее
плотность распределения имеет вид
2
2
()
2
1
()
2
x
m
fx e
. (3.9)
Функция нормального распределения
.
2
1
)(
2
2
mx
t
dtexF (3.10)
Функция Лапласа
x
t
dtex
0
2
2
2
1
)( . (3.11)
Числовые характеристики нормального распределения:
,][ m
X
M
,][
2
XD .][
X
(3.12)
Вероятность попадания на интервал:
m
m
t
mm
dtexP
2
2
2
1
}{
, (3.13)
{}2Px m
. (3.14)
Задача 3.16
Пассажир выходит на остановке автобуса в некоторый момент време-
ни, никак не связанный с расписанием движения. Автобусы следуют друг за
другом с интервалом τ (по времени). Найти закон распределения случайной
величины Т – интервала времени, которое пассажиру приходится ждать.
Решение задачи
Случайная величина Т, так же как и момент прихода пассажира, име-
ет равномерное распределение на интервале (0; τ).
48
0, 0, ,
()
1
, 0 .
tt
ft
t
Задача 3.17
Цена деления шкалы измерительного прибора равна 0,2. Показания
прибора округляют до ближайшего целого деления. Найти вероятность то-
го, что при отсчете будет сделана
ошибка:
а) меньше 0,04;
б) больше 0,05.
Решение задачи
Х – величина случайной ошибки
измерения.
При
грубых измерениях с округлением результата измерения случай-
ная величина Х имеет
равномерное распределение. При округлении до
ближайшего целого деления случайная величина Х принадлежит интервалу
; ( 0,1; 0,1)
22
X
, где 0, 2
– цена деления. Следовательно,
11
5, 0,1 0,1;
0, 2
()
0, 0,1; 0,1.
x
ft
xx
Вероятность того, что при отсчете будет сделана ошибка меньше 0,04,
равна площади заштрихованной фи-
гуры на рис. 3.1.
20,04
() 0,4
0, 2
PA
.
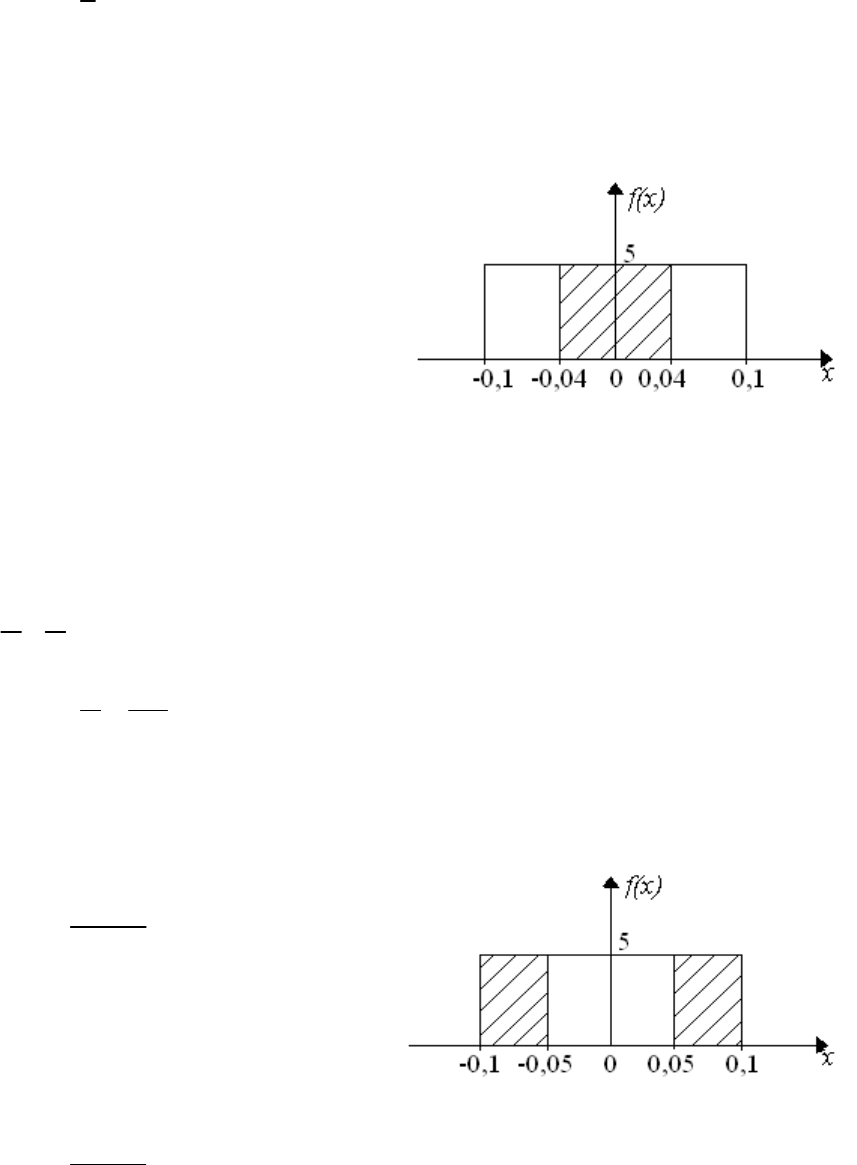
Соответственно, вероятность
того, что при отсчете будет сделана
ошибка больше, чем 0,05, равна
площади заштрихованной фигуры на
рис. 3.2.
20,05
() 0,5
0, 2
P В
.
Задача 3.18
Случайная ошибка измерения подчинена нормальному закону со
среднеквадратическим отклонением σ = 20 мм и нулевым математическим
Рис. 3.1
Рис. 3.2

49
ожиданием. Найти вероятность того, что из трех независимых измерений
ошибка хотя бы одного из них не превысит 4 мм.
Решение задачи
Проводятся точные измерения без округления, следовательно, Х –
случайная ошибка измерения, распределена
нормально с параметрами
0; 20 мм; 4 мм;
x
x
m
Вероятность того, что ошибка одного измерения не превысит 4 мм
(см. формулу (3.14)), равна
4
{ } 2 2 2 0,0793 0,159
20
x
pPXm
.
(в соответствии с прил. 2 значение функции Лагранжа Φ(x) при x = 0,2
равно Φ(x) = 0,0793).
Вероятность того, что ошибка хотя бы одного из трех измерений не
превысит 4 мм:
33
( ) 1 (1 ) 1 (1 0,159) 1 0,596 0,404.PA p
Задача 3.19
Случайная величина Х распределена нормально с математическим
ожиданием
10
x
m мм и среднеквадратическим отклонением σ 5
x
мм.
Найти интервал, в который с вероятностью 0,9973 она попадет в результате
проведенных испытаний.
{ } 2 0,9973
x
PX m
.
(; )
x
x
Х mm
.
В соответствии с прил. 2 в том случае, когда функция Лагранжа
Φ(x) = 0,49865, её аргумент равен x = 3.
0,49865 3; 3σ 35 15 мм;
σσ
(5; 25).
Х
Задача 3.20
Автомат штампует детали, длина которых Х распределена нормаль-
но с математическим ожиданием (проектная длина), равным 50мм. Факти-
ческая длина изготовленных деталей не менее 32 мм и не более 68 мм.
Найти вероятность того, что длина наугад взятой детали:
а) больше 55 мм;
б) меньше 40 мм.
Решение задачи
50 мм
x
m
. Считается, что нормально распределенная случайная ве-
личина Х почти достоверно (с вероятностью, равной P = 0,9973) принадле-

50
жит заданному интервалу (32 мм, 68 мм). Следовательно, длина этого ин-
тервала равна 3σ
x
.
{32 68} { 50 18} 0,9973 3 18 мм, 6 мм.
хх
PP Х PX
Согласно формуле (3.13)
68 50 55 50
( ) { 55} {55 68} 0, 5 0, 2967 0, 203.
66
P А P Х PX
40 50 32 50
( ) { 40} {32 40} 0,4515 0,5 0,076.
66
P В P Х PX
Задача 3.21
Производится взвешивание без систематических ошибок. Случайные
ошибки подчинены нормальному закону распределения с параметром
σ 20
x
г.
а) найти вероятность того, что взвешивание будет произведено с
ошибкой, не превосходящей по абсолютной величине 10 г;
б) найти интервал, в который с вероятностью, равной 0,9, попадет
ошибка взвешивания.
Решение задачи
0; σ 2 г; 10 г; 0,9
x
x
m .
a)
10
( ) { } 2 2 2 0,1915 0,383
σ 20
x
РА PX m
в соответствии с прил. 2 находим, что значение
arg 0,5 0,1915 .
b)
(; )
x
x
Х mm
. ε = ?
{}2;
σσ2
x
PX m
,
σ arg
2
.
0,9
20arg 20 1,654 32,9мм
2
. ( 32,9; 32,9).Х
Задача 3.22
Систематическая составляющая ошибки удержания высоты самолета
равна +20 м, а случайная составляющая ошибки имеет нормальное распре-
деление с с.к.о., равным σ 75
м. Для полета самолета отведен коридор,
высотой 100 м. Какова вероятность
а) что самолет будет лететь ниже коридора;
б) внутри коридора;
с) выше коридора?
Решение задачи
