Самусевич Г.А. Теория вероятностей в примерах и задачах. Теория вероятностей и математическая статистика
Подождите немного. Документ загружается.


21
Всего Окрашенные Остальные
Партия 5 3 2
Выборка 3 1 2
P(
2
A
) =
3,0
3
5
2
2
1
3
C
CC
.
2
() 1 ( ) 10,3 0,7.PA PA
1.4. Частная теорема о повторении опытов
[1, разд. 2.3.1, с. 21 - 23]
Производится n независимых опытов, проводимых в одинаковых
условиях. В каждом из них событие А может появиться с вероятностью
p или не появиться с вероятностью q = 1 – p. Требуется найти вероят-
ность P
m,n
того, что событие А в n опытах появится ровно m раз,
m < n (
формула Бернулли).
,
{}
mmnm
mn n
PPXmCpq
. (1.3)
Вероятность события, состоящего в том, что событие А появится
в n опытах не менее чем m раз (больше или равно m)
1
,
0
{} 1 .
nm
kknk kknk
mn n n
km k
RPXm Cpq Cpq
(1.4)
Задача 1.23
Изделия содержат 5 % брака. Найти вероятность того, что среди 5
наугад взятых изделий:
А = {не окажется ни одного бракованного};
В = {окажется два бракованных изделия}.
Решение задачи
Условия задачи соответствуют частной теореме о повторении опытов
(5 независимых опытов с равной вероятностью наличия бракованных изде-
лий в каждом из них). Справедлива формула Бернулли (1.3).
Вероятность взять бракованное изделие p = 0,05, вероятность взять
годное изделие q=1 - p = 0,95; n = 5.
Событие A (m = 0).
505 5
5
( ) 0,95 0,774PA Cpq.
Событие B (m = 2).
223 2 3
5
54
( ) 0,05 0,95 0,0021
12
PB C pq
.
Задача 1.24
Производится три независимых выстрела по мишени. Вероятности
попадания в мишень при первом, втором и третьем выстрелах равны соот-
ветственно
123
, , ppp
. Найти вероятности того, что в мишень попадает:
А = {ровно два попадания};
В = {хотя бы одно попадание}.
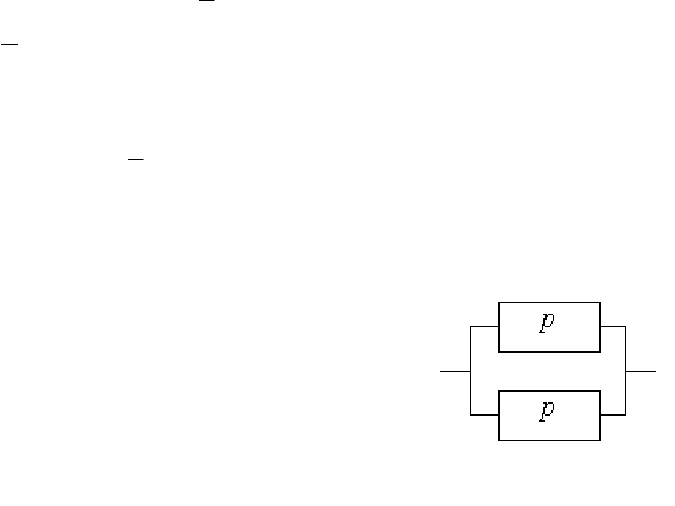
22
Рис. 1.21
Решение задачи
Условия задачи, соответствующие общей теореме о повторении
опытов
. ;
21
pp ;
32
pp
13
;
p
p
1, 1, 2, 3.
ii
qpi
;)(
321321321
ppqpqpqppAP
.1)(
321
qqqBP
Условия задачи, соответствующие частной теореме о повторе-
нии
опытов (применима формула Бернулли (1.3)):
;
321
pppp ,1
ii
pq
3, 2.nm
;)(
22
3
qpCAP .1)(
300
3
qpCBP
1.5. Надежность
[1, разд. 2.3.2, с. 23 - 25]
Надежность
системы определяется вероятностью ее безотказной
работы
в течение заданного интервала времени Т.
Возникновение отказов системы связано с отказами ее элементов.
Таким образом, надежность системы зависит от
надежности ее эле-
ментов
и от схемы их соединения. Надежность k-го элемента
k
p ,
kk
pq 1 , – вероятность его отказа.
Любая схема состоит из параллельного и последовательного соеди-
нений элементов.
Надежность параллельного соединения элементов
Событие
A
= {работает хотя бы один элемент},
Противоположное событие
A = {отказ всех элементов}.
321
1)(1)( qqqAPAP
. (1.5)
Надежность последовательного соединения элементов
Событие
A = {работают все элементы (безотказная работа схемы)},
Противоположное событие
A = {отказ хотя бы одного элемента}.
321
)( pppAP
. (1.6)
Задача 1.25
Для повышения надежности p прибора он
дублируется еще одним таким же прибором. Если
первый отказал, происходит автоматическое (и
безотказное) переключение на дублирующий при-
бор. Приборы отказывают независимо друг от дру-
га. Найти вероятность того, что система из двух при-
боров проработает безотказно время Т.

23
Решение задачи
На рис. 1.21 изображена схема результирующего прибора, представ-
ляющая собой параллельное соединение исходных приборов. Надежность
схемы равна вероятности события А = {работает хотя бы один прибор}. В
соответствии с формулой (1.5)
22
() 1 () 1(1 ) 1PA PA p q .
Задача 1.26
Прибор имеет надежность p. Он дуб-
лируется таким же прибором, но переклю-
чающее устройство имеет надежность p
ny
.
Найти надежность системы (см. рис.1.21a).
ny
() 1(1 )(1 ).PA p p p
Задача 1.27
Приведены схемы соединений элементов, образующих цепь с одним
входом и одним выходом. Отказы элементов – независимые в совокупности
события. Надежность каждого элемента
k
p
,
kk
pq 1 – вероятность его отказа. Вычислить
надежность (вероятность события A) каждой схе-
мы.
Решение задачи
Схема устройства 1 представлена на
рис. 1.22 (параллельное соединение трех элемен-
тов). Событие А = {работает хотя бы один эле-
мент}.
Согласно формуле (1.5)
123
() 1PA qqq .
Схема устройства 2 пред-
ставлена
на рис. 1.23 (две ветви по-
следовательно соединенных трех
элементов).
1123
Pppp – вероятность того,
что работает первая ветвь (последовательное соединение – формула (1.6)).
2 456
Pppp – вероятность того, что работает вторая ветвь (последова-
тельное соединение – формула (1.6)).
1 1
(1 )PP – вероятность того, что отказал хотя бы один элемент 1-й
ветви.
Рис. 1.23
p
p
p
пу
Рис. 1.21a
Рис. 1.22
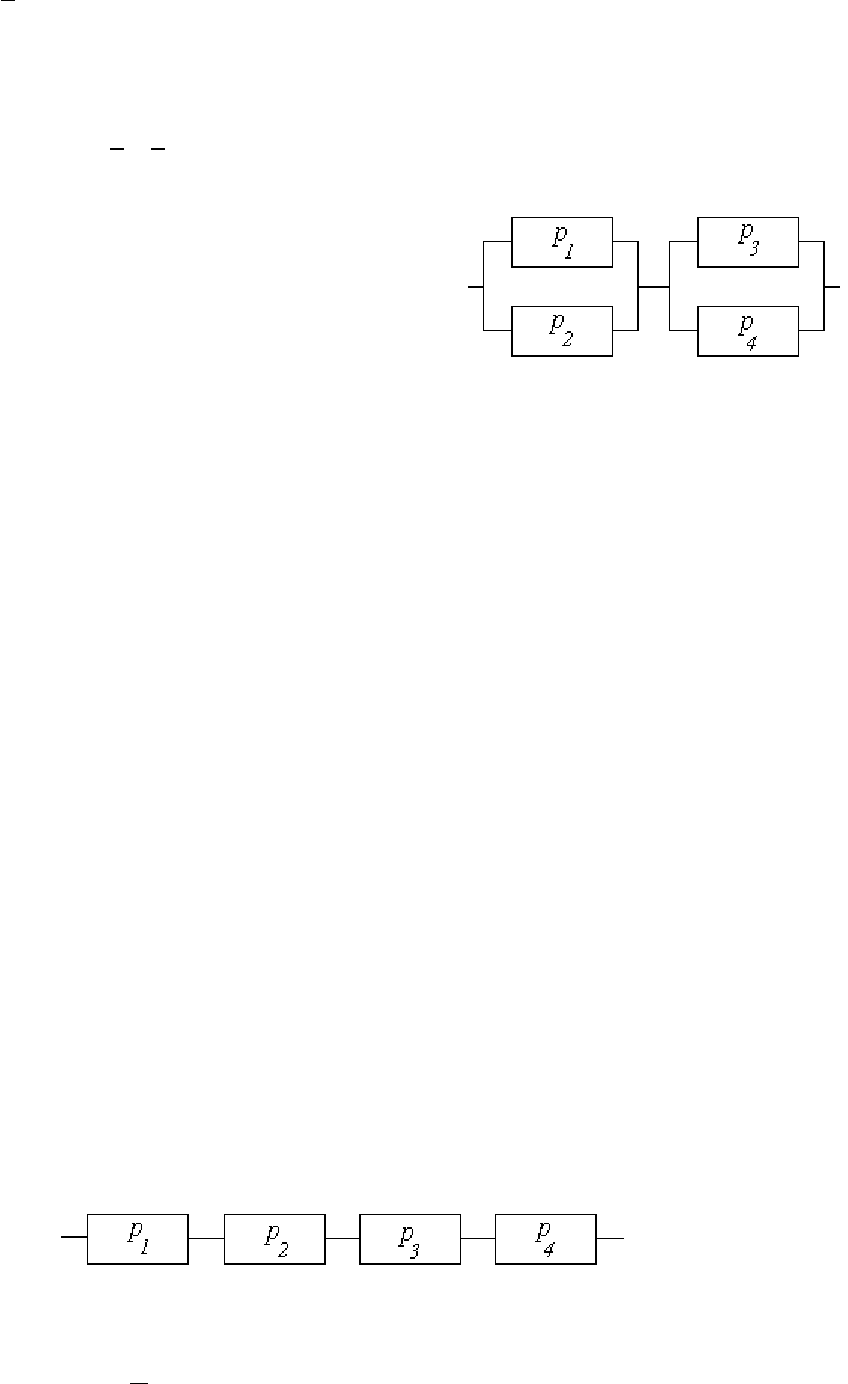
24
22
(1 )PP – вероятность того, что отказал хотя бы один элемент 2-й
ветви.
Надежность схемы согласно формуле (1.5) равна (параллельное со-
единение двух блоков)
1 2 1 2 123 456
( ) 1 1 (1 )(1 ) 1 (1 )(1 ).
P
APP PP pppppp
Схема устройства 3 представ-
лена на рис. 1.24 (два блока элементов, со-
единенные последовательно).
Событие A
1
– надежность блока 1,2
(параллельное соединение двух элементов
блока – формула (1.5)).
11212
()1(1 )(1 )1 .PA p p qq
Событие A
2
– надежность блока 3,4 (параллельное соединение двух
элементов блока – формула (1.5)).
23412
()1(1 )(1 )1 .PA p p qq
Надежность всей схемы (последовательное соединение двух блоков
– формула (1.6)).
12
() ( ) ( )PA PA PA
=
12 34
(1 )(1 ).qq qq
Задача 1.28
Имеются 4 потребителя электрического тока. Вероятность отклю-
чения
первого из них равна p
1
= 0,6, второго p
2
= 0,2, остальных p
3
= p
4
=
= 0,3. Найти вероятность того, что генератора тока будет
отключен, если
потребители соединены в соответствии со схемами, представленными на
рис. 1.25 и 1.26 (сложность этой задачи в том, что в ней p
k
– вероят-
ность отключения k - го потребителя тока, а q
k
= 1-p
k
– вероятность
его работы).
Решение задачи
1. Событие A = {отключение генератор тока в случае, когда все
потребители соединены последовательно (см. рис. 1.25)}.
Событие А = {отключен хотя бы один потребитель};
Событие
A
= {все потребители тока работают}.
Рис. 1.25
Рис. 1.24
25
Рис. 1.26
Согласно формуле (1.16)
2
123
() (1 )(1 )(1 )PA p p p =
2
0, 4 0,8 0,7 0,157 .
( ) 1 ( ) 1 0,077 0,843.PA PA
2.
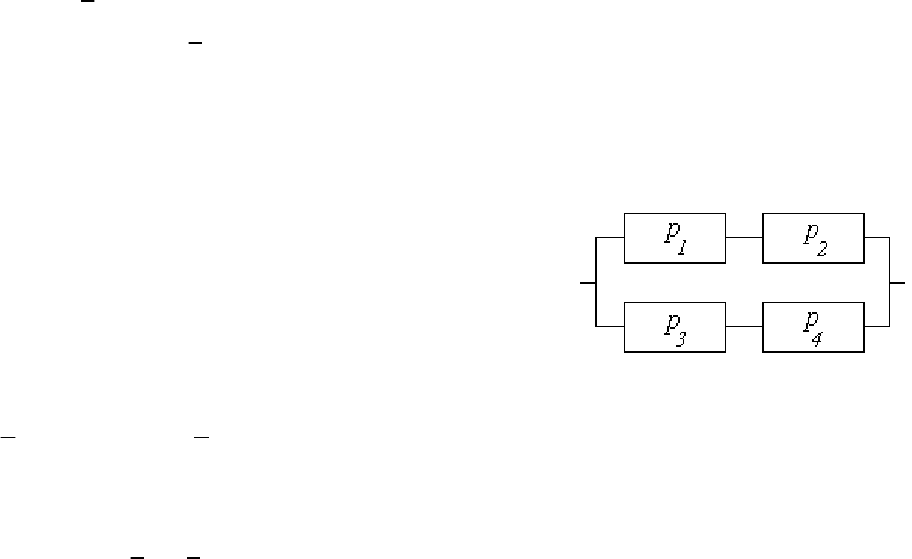
Событие B = {отключение генератора тока в случае, когда по-
требители соединены по схеме рис. 1.26}.
Генератор отключен, если
отказали обе пары потребителей.
P
1,2
– вероятность того, что работает
первая, P
3,4
– вероятность того, что работает
вторая пара потребителей.
1, 2 1 2 1 2
(1 )(1 ) 0, 4 0,8 0,32;Pppqq
22 2
3,4 3 3
(1 ) 0, 7 0, 49Ppq .
1,2 1,2
1PP
и
3,4 3,4
1PP
– вероятности отказа хотя бы одного потре-
бителя соответствующей пары. Вероятность того, что разорваны обе цепи
(см. формулу (1.5)).
1, 2 3, 4 1, 2 3, 4
( ) (1 ) (1 ) (1 0,32) (1 0,49) 0,347.PB P P P P
1.6. Формула полной вероятности
[1, разд. 2.3.3, с. 25 - 27]
Проводится опыт, об условиях которого можно сделать n исклю-
чающих друг друга предположений – гипотез.
Гипотезы – это попарно
несовместные события, образующие полную группу:
n
HHH ...
21
,
ji
HH, , 1, 2, ..., ij n
.
Вероятности гипотез
)(,...),(),(
21 n
HPHPHP ,
n
i
i
HP
1
1)( .
Рассматривается
событие А, которое может появиться только с
одной из гипотез. Заданы условные вероятности появления события А при
осуществлении условий опыта для каждой гипотезы:
12
(/ ), (/ ), ..., (/ )
n
PAH PAH PAH .
Безусловная вероятность )(
A
P
события А определяется по формуле
полной вероятности:
n
i
ii
HAPHPAP
1
)/()()(
. (1.7)
Задача 1.29

26
Прибор состоит из двух дублирующих узлов и может работать в двух
режимах: нормальном (80 % случаев) и неблагоприятном (20 % случаев).
Надежность каждого узла в нормальном режиме равна 0,9, в неблагоприят-
ном режиме – 0,6. При выходе из строя узла происходит безотказное пере-
ключение на дублера. Найти надежность прибора.
Решение задачи
Событие А = {безотказная работа прибора (его надежность)}.
Вводятся гипотезы:
Гипотеза Н
1
= {прибор работает в нормальном режиме};
;8,0)(
1
HP
p
1
= 0,9.
Гипотеза Н
2
= {прибор работает в неблагоприятном режиме},
;2,0)(
2
HP p
2
= 0,6.
Условные вероятности (безотказная работа параллельного соединения
двух узлов):
2
1
( / ) 1 (1 0,9) 0,99PAH ;
2
2
( / ) 1 (1 0, 6) 0,84PAH .
Применяя формулу (1.7), получим
.96,084,02,099,08,0)/()()/()()(
2211
HAPHPHAPHPAP
Задача 1.30
Сообщение передается по одному из n каналов связи. При этом, n
1
каналов связи находятся в отличном состоянии, n
2
– в плохом, n
3
– в по-
средственном состояниях. Вероятности правильной передачи для них p
1
, p
2
и p
3
соответственно. Для повышения достоверности сообщение передается
два раза по одному каналу, выбираемого наугад. Найти вероятность того,
что хотя бы одно сообщение из двух будет передано верно.
Решение задачи
Событие А
= {сообщение будет передано верно}.
Гипотеза Н
1
= {сообщение будет передано по отличному каналу};
11
() /PH n n .
Гипотеза Н
2
= {сообщение будет передано по плохому каналу};
22
() /PH n n .
Гипотеза Н
3
= {сообщение будет передано по посредственному ка-
налу};
33
() /PH n n .
A
= { неверно переданы оба сообщения, последовательно передавае-
мые по одному каналу}.
;)1()/(
2
11
pHAP
2
22
(/ ) (1 );PAH p
2
33
(/ )(1 )PAH p
.

27
В соответствии с формулой (1.7) имеем
.)1()1()1()(
2
3
3
2
2
2
2
1
1
p
n
n
p
n
n
p
n
n
AP
() 1 ()PA PA
=
222
3
12
123
1(1) (1) (1).
n
nn
ppp
nn n
Задача 1.31
Производится посадка самолета. При хорошей погоде вероятность
благополучной посадки равна p
1
, при плохой – p
2
. Приборы, обеспечива-
ющие посадку, имеют надежность P. При плохой погоде и отказавших при-
борах вероятность посадки p
3
. Плохая погода случается в k % случаях.
Найти вероятность благоприятной посадки самолета.
Решение задачи
Событие А
= {благополучная посадка самолета}; P(A) = ?
Гипотеза Н
1
= {посадка осуществляется при хорошей погоде};
1
( ) 1 /100PH k .
Гипотеза Н
2
= {посадка осуществляется при плохой погоде};
2
() /100PH k .
11
(/ )PAH p (благополучная посадка самолета при хорошей погоде).
12 2
(/ )PA H P p
(благополучная посадка самолета, если приборы ра-
ботают
при плохой погоде).
22 3
(/ )(1 )PA H P p
(
благополучная посадка самолета, если приборы
отказали при плохой погоде).
В соответствии с формулой (1.7) получим
123
() (1 ) (1 ) .
100 100
kk
PA p P p Pp
Задача 1.32
Производятся три выстрела с вероятностями попадания 0,4; 0,5; 0,7.
Для вывода объекта из строя достаточно трех попаданий; при двух попада-
ниях он выходит из строя с вероятностью 0,6; при одном – с вероятностью
0,2. Найти вероятность вывода объекта из строя.
Решение задачи
Событие А
= {объект выведен из строя}; P(A) = ?
Гипотеза Н
0
= {в объект не попал ни один снаряд}.
Гипотеза Н
1
= {в объект попал один снаряд}.

28
Гипотеза Н
2
= {в объект попали 2 снаряда}.
Гипотеза Н
3
= {в объект попали 3 снаряда}.
0
( ) 0,6 0,5 0,3PH ;
;36,07,05,06,03,05,06,03,05,04,0)(
1
HP
;41,07,05,06,07,05,04,03,05,04,0)(
2
HP
3
()0,40,50,70,14PH
.
0
(/ ) 0;PAH
;2,0)/(
1
HAP
;6,0)/(
2
HAP
3
(/ )1PAH
.
Итак, в соответствии с формулой (1.7) получим
.458,0114,06,041,02,036,0)(
A
P
1.7. Теорема гипотез (формула Байеса)
[1, разд. 2.3.4, с. 27 - 28]
До опыта об условиях его проведения был выдвинут ряд гипотез
12
, , ...,
n
H
HH, несовместных и образующих полную группу событий
n
i
i
H
1
,
ji
HH,
j
i
i,j = 1, 2, …, n.
Априорные вероятности гипотез (вероятности гипотез до опыта):
12
( ), ( ), ..., ( );
n
PH PH PH
n
i
i
HP
1
1)( .
Апостериорные вероятности (вероятности гипотез после опыта)
– это
условные вероятности гипотез при условии, что в результате опы-
та событие А произошло
12
( / ), ( / ), ..., ( / )
n
PH A PH A PH A.
Для вычисления апостериорных вероятностей существует
формула
Байеса
)(
)/()(
)/(
AP
HAPHP
AHP
ii
i
, 1, 2, ..., in
, (1.8)
n
i
ii
HAPHPAP
1
)/()()( .
Задача 1.32
Имеются 3 урны. В первой из них 3 белых и 1 черный шар, во второй
– 2 белых и 3 черных, в третьей – 3 белых шара. Вынутый из наугад взятой
урны шар оказался белым. Найти апостериорные вероятности гипотез, т.е.

29
вероятности того, что этот шар был вынут из первой, второй или третьей
урны соответственно.
Решение задачи
Событие A
= {вынуть белый шар}.
Гипотезы: H
i
= {достать шар из i - й урны, i = 1, 2, 3}.
Априорные вероятности гипотез:
123
() ( ) ()1/3PH PH PH.
Условные вероятности появления события
А (вынуть белый шар) для
каждой гипотезы
;
4
3
)/(
1
HAP
;
5
2
)/(
2
HAP
3
(/ )1PAH
.
В соответствии с формулой (1.7) получим
13 12 1 43
()
34 35 3 60
PA .
Апостериорные вероятности гипотез:
;
43
15
43
60
60
15
)/(
1
AHP
;
43
8
)/(
2
AHP
.
43
20
)/(
3
AHP
Таким образом, благодаря полученной дополнительной информации о
том, что вынутый шар оказался белым, увеличилась вероятность того, что
этот шар был вынут именно из третьей урны. Этого следовало ожидать, по-
скольку в третьей урне был наибольшим процент белых шаров. Во второй
урне этот процент был наименьшим, потому уменьшилась апостериорная
вероятность второй гипотезы.
Задача 1.33
Два стрелка независимо друг от друга стреляют по одной мишени,
делая по одному выстрелу. Вероятности попадания равны 0,8 и 0,4. После
стрельбы обнаружена одна пробоина. Найти вероятность того, что она при-
надлежит первому стрелку.
Решение задачи
Событие А
= {в результате стрельбы появилась одна пробоина}.
Гипотеза H
1
= {оба стрелка не попадут}.
Гипотеза H
2
= {оба стрелка попадут}.
Гипотеза H
3
= {первый стрелок попал, второй нет}.
Гипотеза H
4
= {второй стрелок попал, первый нет}.
Априорные вероятности гипотез:
;12,06,02,0)(
1
HP ;32,04,08,0)(
2
HP
;48,06,08,0)(
3
HP ;08,04,02,0)(
4
HP
1
1, 000
n
i
i
H
.

30
;0)/()/(
21
HAPHAP
34
(/ ) (/ )1PAH PAH
.
В соответствии с формулой (1.7) имеем
() 0,481 0,081 0,56PA
.
Апостериорные вероятности гипотез (формула Байеса (1.8)):
;86,0
7
6
56,0
148,0
)/(
3
AHP
.14,0
7
1
56,0
108,0
)/(
4
AHP
Первый стрелок стреляет значительно лучше второго. Поэтому следо-
вало ожидать увеличения апостериорной вероятности того, что именно пер-
вый стрелок попал в мишень.
Задача 1.34
Два из трех независимо работающих элемента вычислительного
устройства отказали. Найти вероятность того, что отказали первый и второй
элементы, если априорные вероятности их отказов соответственно равны:
p
1
= 0,2; p
2
= 0,4; p
3
= 0,3.
Решение задачи
Событие А
= {отказали два элемента}.
Гипотеза H
1
= {отказали 1 и 2 элементы}.
Гипотеза H
2
= {отказали 1 и 3 элементы}.
Гипотеза H
3
= {отказали 2 и 3 элементы}.
Априорные вероятности гипотез:
1123
( ) 0, 2 0, 4 0,7 0,056;PH ppq
;036,03,06,02,0)(
3212
pqpHP
3123
( ) 0,8 0, 4 0,3 0,096PH qpp.
123
(/ ) (/ ) (/ )1PAH PAH PAH.
Перечисленные гипотезы не образуют полную группу событий (сум-
ма их вероятностей не равна единице), но условные вероятности события A
равны нулю для всех других возможных гипотез, образующих группу.
В соответствии с формулой полной вероятности (1.7)
( ) 0,056 1 0,036 1 0,096 1 0,188PA.
Апостериорные вероятности гипотез (формула Байеса (1.8)):
;3,0
188,0
056,0
)/(
1
AHP
;19,0
188,0
036,0
)/(
2
AHP
.51,0
188,0
096,0
)/(
3
AHP
Задача 1.35
