Самусевич Г.А. Теория вероятностей в примерах и задачах. Теория вероятностей и математическая статистика
Подождите немного. Документ загружается.

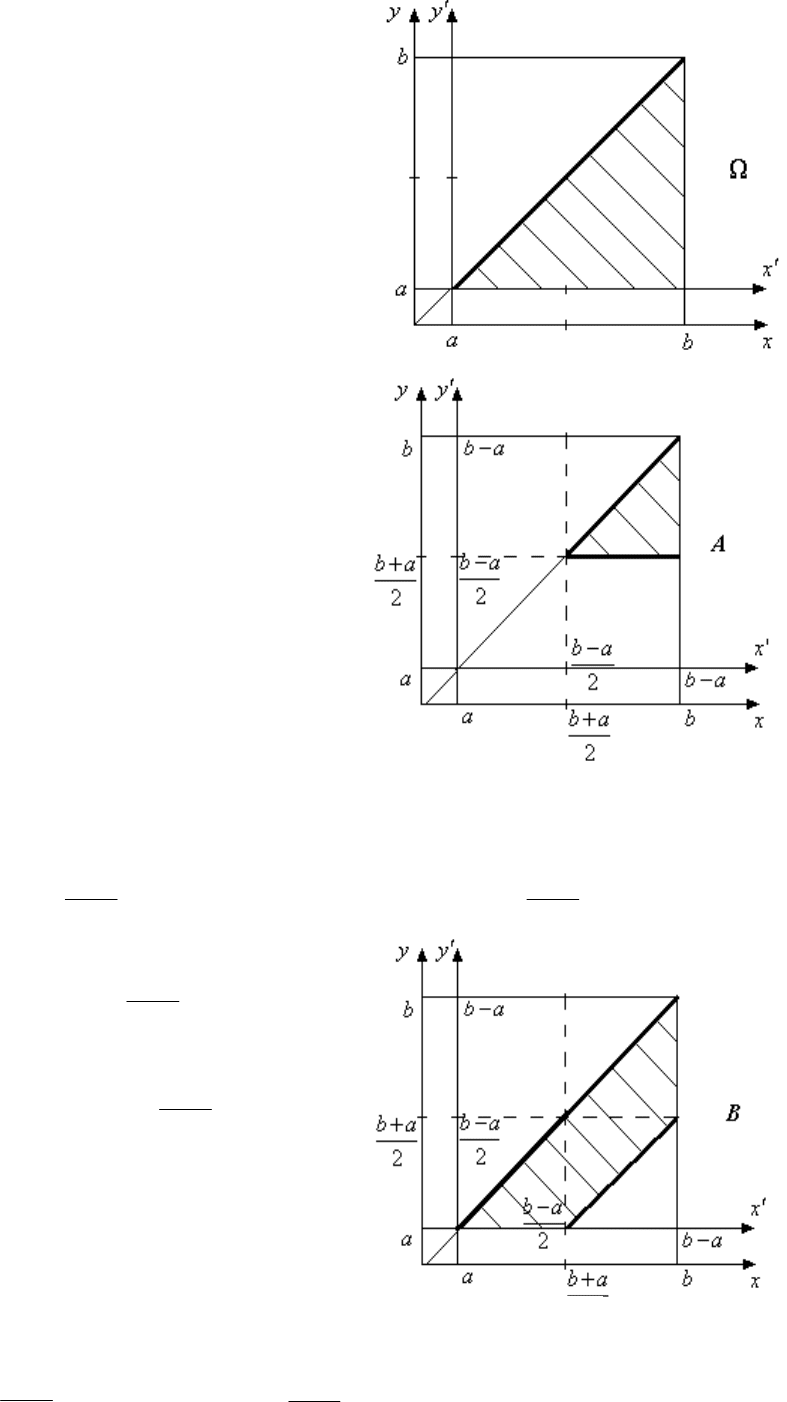
11
Решение задачи
На рис. 1.11 – 1.14 событиям , A,
B, C
соответствуют заштрихованные об-
ласти. Жирной линией выделены наибо-
лее важные границы областей. Вводится
вспомогательная система координат,
начало которой находится в точке (
a, a).
ayyaxx
,
.
Множество элементарных
исходов
отображено на рис. 1.11.
= {
x
yab
x
a
,
,
yx
}.
Граница области
yx
. Координа-
ты контрольной точки , 0
xby
удо-
влетворяют неравенству
yx
(точка
принадлежит допустимой области). Сле-
довательно, множество
содержит точ-
ки, принадлежащие границе и лежащие
ниже её.
Множество A (рис. 1.12)
является пересечением множества
и
подмножества точек
A
1
, координаты ко-
торого удовлетворяют дополнительному
неравенству
byya .
À
,
2
ba
y
(byya
,
2yba
,
2
ba
y
).
Граница подмножества
A
1
опреде-
ляется равенством
2
ab
y
. Координаты
контрольной точки
x
yb
удовле-
творяют неравенству
2
ba
y
. Следо-
вательно, все точки подмножества
A
1
лежат
выше его границы.
Множество B (рис. 1.13)
есть пересечение
множеств и B
1
. До-
полнительное неравенство, определяю-
щее подмножество
B
1
,
2
ab
yx
.
B
,
2
ab
yx
.
Рис. 1.11
Рис. 1.12
Рис. 1.13
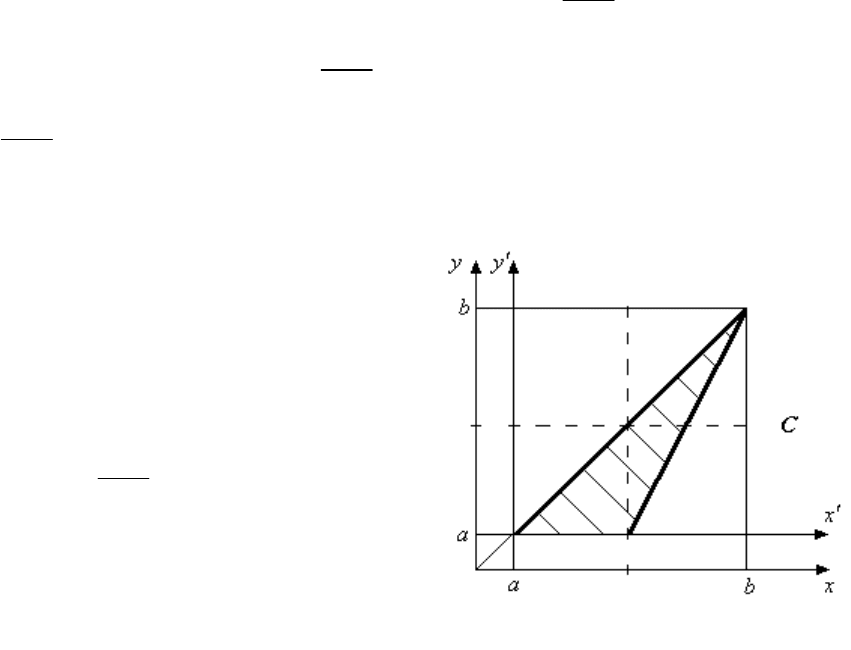
12
Уравнение границы подмножества B
1
2
ba
xy
. Координаты
контрольной точки
0, 0
2
ba
xy
удовлетворяют неравенству
2
ab
yx
. Следовательно, все точки подмножества B
1
лежат выше его
границы.
Множество C (рис. 1.14):
Дополнительное неравенство, опре-
деляющее подмножество
C
1
,
x
by
x
.
C ,
by
x
2
.
Уравнение границы подмножества
C
1
by
x
2
(прямая, проходящая через
точки
, ; ,
2
ba
yax ybxb
). Кон-
трольная точка (
a,a) ( ay
x
,
2aaab) лежит в допустимой области.
Следовательно, все точки подмножества
C
1
лежат выше его границы.
Пар несовместных событий нет.
Задача 1.10
Иван и Петр договорились о встрече в определенном месте между
одиннадцатью и двенадцатью часами. Каждый приходит в случайный мо-
мент времени указанного промежутка и ждет другого до истечения часа, но
не более 15 минут, после чего уходит. Наблюдаемый результат – пара чисел
(
x,y), где x – время прихода Петра, y – время прихода Ивана. Построить
множество элементарных исходов и подмножества, соответствующие при-
веденным событиям.
А = {встреча состоялась};
В = {Петр ждал и не дождался};
С = {Ивану не пришлось ждать Петра};
D = {встреча состоялась после 11ч 30 мин};
E = {Иван опоздал на встречу}.
Решение задачи
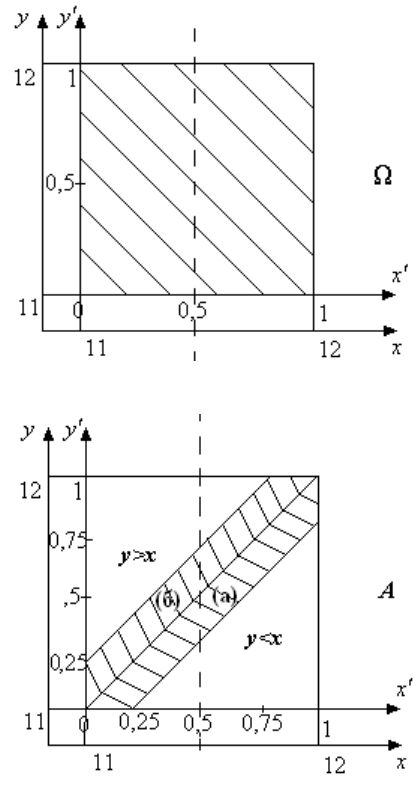
На рис. 1.15 – 1.20 событиям , A, B, C, D, E соответствуют
заштрихованные области. Вводится вспомогательная система координат с
началом точке с координатами (11, 11).
Рис. 1.14
13
11, 11xx yy
.
Множество элементар-
ных
исходов (рис. 1.15):
{11 12, 11 12;
0 1, 0 1}.
x
y
xy
Множество A (рис. 1.16)
является подмножеством множества
.
Кроме того, оно представляется сум-
мой двух подмножеств
A
1
и A
2
, получа-
емых в результате рассмотрения двух
вариантов.
Вариант а. Иван пришел вместе с
Петром или раньше его, но ждал Петра
не более 0,25 часа (пересечение двух
областей
1
A
и
1
A
).
А
, yx
,
0, 25xy
.
yx
(допустимой являет-
ся область
1
A
, точки которой находятся
ниже и на прямой yx
).
0, 25xy
(границей яв-
ляется прямая 0, 25
xy
, координа-
ты контрольной точки
1, 0xy
не
удовлетворяют неравенству 0, 25
xy
, следовательно, допустимой явля-
ется область
1
A
, точки которой находятся выше и на границе
0,25xy
).
Вариант б. Петр пришел вместе с Иваном или раньше его и ждал
Ивана не более 0,25 часа.
А
,
x
y
,
0,25yx
.
x
y
(допустимая область
2
A
, точки которой находятся выше
и на прямой yx
).
0, 25yx
(границей является прямая 0,25yx
, коорди-
наты контрольной точки
0, 1xy
не удовлетворяют неравенству
0, 25
yx
, следовательно, допустимой является область
2
A
,
находящаяся
ниже и на границе 0,25yx
).
Рис. 1.15
Рис. 1.16
14
Множество B (рис. 1.17)
является подмножеством множества
;
представляется суммой двух подмно-
жеств, получаемых в результате рассмот-
рения двух вариантов.
Вариант а. Иван пришел раньше, но
Петр пришел слишком поздно и Иван его
не дождался.
B , yx
,
0, 25xy
.
Допустимой является область, точки
которой одновременно находятся
ниже
прямой
yx
и ниже и на границе 0,25xy
.
Вариант б. Иван пришел поздно, Петр пришел раньше, ждал 15 мин и
ушел.
B ,
x
y
, 0,25yx
.
Допустимой является область, точки
которой одновременно находятся
выше
прямой
yx
и выше и на границе
0,25yx
.
Множество C (рис. 1.18) яв-
ляется подмножеством множества
. Петр
пришел раньше или вместе с Иваном, Иван
пришел за Петром в пределах 15 мин. (см.
вариант
б множества A).
C
,
x
y
, 0,25yx
.
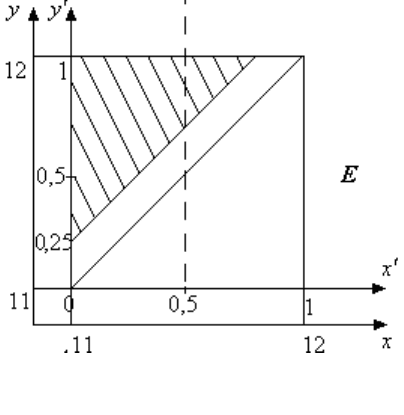
Множество D (рис. 1.19) яв-
ляется подмножеством множества
;
представляется суммой двух подмножеств,
получаемых в результате рассмотрения
двух вариантов.
Вариант а. Иван пришел раньше,
Петр пришел за ним в пределах 15 мин, но
после 11,5 часов (см. вариант
а множества
A с дополнительным условием
11,5; 0,5
xx
).
D, yx
,
0, 25xy
,
11,5; 0,5
xx
.
Рис. 1.17
Рис. 1.18
Рис. 1.19
15
Вариант б. Петр пришел раньше,
Иван пришел за ним в пределах 15 мин.,
но после 11,5 часов (см. вариант
б множе-
ства
A с дополнительным условием
11,5; 0,5
xx
).
D,
x
y
, 0,25yx
,
11,5; 0,5yy
Множество E (рис. 1.20):
Петр пришел раньше, Иван опоздал
(см. вариант б множества
B).
E
,
x
y
, 0,25yx
.
1.3. Непосредственный подсчет вероятностей
[1, разд. 2.1, 2.2, с. 13-21]
События A
i
образуют полную группу, если в результате опыта обя-
зательно должно произойти
хотя бы одно событие этой группы и ника-
кое другое
n
i
i
A
1
.
Случаи – это несовместные равновозможные события, образую-
щие полную группу.
Если опыт сводится к схеме случаев, то справедлива классическая
формула
(1.1).
Задача 1.11
Наудачу выбирается пятизначное число. Найти вероятности событий:
А = {число одинаково читается как слева направо, так и справа нале-
во};
B = {число кратно пяти}.
5
()10nN (число состоит из 5 независимых знаков, каждый из ко-
торых имеет 10 значений – схема выбора с возвращением и упорядочением
элементов).
Событие А
В составе числа, принадлежащего множеству A, только 3 знака яв-
ляются независимыми
.
А
= {x y z y x},
9,,0
z
y
x
,
,10)(
3
ANm
01,0)(
A
P
.
Рис. 1.20
16
Событие B
Задача может быть решена двумя методами.
1. В составе числа, принадлежащего множеству
B, 4 знака могут
быть выбраны произвольно. Каждый из них независимо от других прини-
мает одно из 10 значений. В пятом разряде – только два числа: 0 и 5.
5
()10nN ,
4
() 210,
b
mNB
4
5
210
() 1/5
10
PB
.
2. Независимо от того, сколько и какие значения имеет данное число в
первых четырех разрядах, оно кратно пяти, если оканчивается на ноль или
на пять. Таким образом, искомую вероятность определяет только число в
последнем разряде так, как если бы оно был одно.
()10nN, () 2
b
mNB, () 1/5PB
.
Задача 1.12
Для беспрепятственного полета над некоторой территорией самолет
посылает по радио контрольную кодовую группу, состоящую из точек и ти-
ре. Найти вероятность того, что радист угадает кодовую группу, если число
элементов в ней равно семи.
7
( ) 2 128, ( ) 1, ( ) 1/128
m
NN mNA PA
n
.
Задача 1.13
Числа 1, 2, … , n расположены случайным образом.
Найти вероятность того, что числа 1, 2, 3 расположены в поряд-
ке возрастания и
обязательно рядом.
В одной группе не может быть одинаковых элементов (схема выбора
без возвращения), но порядок расположения элементов в группе имеет
значение (упорядочение элементов в группе). Число таких групп равно
числу размещений
m
n
A
. Первая цифра заданной группы может занять n - 2
позиции, остальные две цифры к ней «прилеплены». Следовательно, число
благоприятных случаев равно () 2mNA n
.
3
() ( 1)( 2),
n
NN A nn n
1
() 2, () .
(1)
mNA n PA
nn
Найти вероятность того, что числа 1, 2, 3 расположены в поряд-
ке возрастания, но
не обязательно рядом.
Поскольку значение имеет только расположение чисел 1, 2, 3, а рас-
положение других чисел – безразлично, то можно считать, что группа со-
стоит только из этих чисел и общее число случаев равно числу перестано-
вок. Благоприятным является только один случай.
3
3
() 6,nN A () 1, () 1/6mNB PB .

17
Задача 1.14
В пачке двадцать перфокарт, помеченных номерами 101, 102, … , 120
и произвольно расположенных. Найти вероятность того, что наудачу вы-
бранные две перфокарты имеют номера 101 и 102.
190
21
1920
2
20
Cn
, ,1
m () 1/190PA
.
Порядок расположения перфокарт в группе значения не имеет (схема
выбора без возвращения и без упорядочения элементов приводит к сочета-
ниям).
Задача 1.15
На полке в случайном порядке расставлено n книг и среди них два
тома некоторого произведения. Найти вероятность того, что оба тома рас-
положены рядом.
2
(1)
n
nA nn ,
)1(2
nm
a
,
nnn
n
n
m
AP
a
2
)1(
)1(2
)(
(возможны два варианта расположения томов: 1,2 или 2,1).
Задача 1.16
Четырехтомное сочинение расположено на полке в случайном поряд-
ке. Найти вероятность того, что тома стоят в должном порядке справа нале-
во или слева направо.
4
4
24nA, 2
a
m , ( ) 1/12PA
.
Задача 1.17
Общество из n человек садится за круглый стол. Найти вероятность
того, что два определенные лица окажутся рядом.
() ( 1),NN n
2
a
m ,
1
2
)(
n
AP .
Первый человек может занять любое из n мест, второй – одно из
(n-1) мест. Учитывается, что из них два места – соседние.
Задача 1.18
Телефонный номер состоит из 4 цифр. Найти вероятность того, что
А = {все цифры различны};
В = {все цифры одинаковы}.
Общее число событий
4
10
n (номер 0000 возможен).
Число событий, благоприятных событию A (группы из четырех
различных цифр, расположение которых имеет значение (схема выбора без
возвращения))
4
10
10 9 8 7,
a
mA
.5,0
10
78910
)(
4
AP

18
Число событий, благоприятных событию B (группы из четырех
одинаковых цифр, таких групп – 10)
,10
b
m
.10
10
10
)(
3
4
BP
Задача 1.19
В урне 5 шаров – 1, 2, 3, 4, 5. Наудачу без возвращения извлекают три
шара. Найти вероятность того, что
А = {последовательно появятся шары 1, 4, 5};
В = {шары имеют номера 1, 4, 5 независимо от того, в какой последо-
вательности они появляются}.
Шары в группе имеют разные номера, расположение их в группе
имеет значение (схема выбора без возвращения с упорядочением элемен-
тов).
3
5
111
()
543 60
PA
A
.
Шары в группе имеют разные номера, расположение их в группе
значение не имеет (схема выбора без возвращения, без упорядочения эле-
ментов).
.
10
1
345
3211
)(
3
5
C
BP
Задача 1.20
Из шести карточек с буквами Л, И, Т, Е, Р, А выбираются наугад в
определенном порядке 4 карточки. Найти вероятность того, что при этом
получится слово «ТИРЕ».
Буквы на карточках в результирующей группе разные, расположение
их в группе имеет значение (схема выбора без возвращения с упорядочени-
ем элементов).
4
6
An ,
11
1, ( )
6543 360
a
a
m
mPA
n
.
Типовая задача
В партии из N деталей M деталей бракованных. Для контроля выби-
рают n (
N
n ) деталей. Найти вероятность того, что ровно m (
M
m
)
деталей будут бракованными.
Для определения общего числа возможных случаев необходимо опре-
делить число способов выбора группы из n деталей из партии, содержа-
щей N деталей (детали разные, их расположение в группе не имеет значе-
ние). Следовательно, рассматриваемый случай относится к схеме выбора
19
без возвращения и без упорядочения элементов и число таких групп в такой
схеме равно
n
N
C .
Число
a
m случаев, благоприятных событию A, определяется числом
способов, какими из М бракованных можно сформировать группу из m
деталей. Это число равно
m
M
C . Но каждой такой группе m бракованных
соответствует комбинация из (n – m) доброкачественных деталей. Таких
комбинаций будет
mn
M
N
C
. Таким образом, искомая вероятность опреде-
ляется отношением
n
N
mn
MN
m
M
C
CC
AP
)( . (1.2)
Задача 1.21
Из 10 билетов 2 выигрышных. Найти вероятность того, что среди 5
билетов:
А = {один выигрышный};
В = {оба выигрышных};
С = {хотя бы один билет выигрышный}.
Решение задачи
Событие A
Вероятность события A вычисляется по формуле (1.2) в соответствии
с данными таблицы:
Всего Выигрышный Остальные
Партия 10 2 8
Выборка 5 1 4
9
5
)(
5
10
4
8
1
2
C
CC
AP
.
Событие B
Вероятность события B вычисляется по формуле (1.2) в соответ-
ствии с данными таблицы:
9
2
)(
5
10
3
8
2
2
C
CC
BP
.
Событие C
Вероятность события C вычисляется по формуле (1.2) в соответ-
ствии с данными таблицы:
Всего Выигрышный Остальные
Партия 10 2 8
Выборка 5 2 3
20
Всего Выигрышный Остальные
Партия 10 2 8
Выборка 5 0 5
05
28
5
10
27
() 1 1 1
99
CC
PC C
C
.
Задача 1.22
В коробке 5 изделий, из них 3 изделия окрашены. Наудачу извлечены
3 изделия. Найти вероятность того, что из них хотя бы два окрашенных.
Решение задачи
Рассматриваются два варианта решения.
1.
Событие A = {два или три изделия окрашены}.
Событие A
1
= {два изделия окрашены, см. таблицу}.
Всего Окрашенные Остальные
Партия 5 3 2
Выборка 3 2 1
P(A
1
) = 6,0
10
6
3
5
1
2
2
3
C
CC
.
Событие A
2
= {три изделия окрашены, см. таблицу}.
Всего Окрашенные Остальные
Партия 5 3 2
Выборка 3 3 0
P(A
2
) =
1,0
10
1
3
5
0
2
3
3
C
CC
. P(A) = P(A
1
) +
2
( ) 0, 6 0,1 0,7.PA
2. С
обытие
A
, противоположное событию A = {ни одно изделие
не окрашено или одно изделие окрашено}.
Событие
1
A
= {ни одно из трех изделий не окрашено} (см. таб-
лицу).
Всего Окрашенные Остальные
Партия 5 3 2
Выборка 3 0 3?
P(
1
A
) = 0. (событие
1
A
недостоверно, поскольку неокрашенных де-
талей в коробке только две).
Событие
2
A
= {одно изделие окрашено, см. таблицу}.
