Самусевич Г.А. Теория вероятностей в примерах и задачах. Теория вероятностей и математическая статистика
Подождите немного. Документ загружается.

31
Телеграфное сообщение состоит из сигналов «точка» и «тире». Ста-
тистические свойства помех таковы, что искажаются в среднем 2/3 сообще-
ний «точка» и 1/3 сообщений «тире». Известно, что среди передаваемых
сигналов «точка» и «тире» встречаются в отношении 5:3. Определить веро-
ятности того, что принят передаваемый сигнал, если:
а) принят сигнал «точка» (передана «точка»);
б) принят
сигнал «тире» (передано «тире»).
Решение задачи
Событие А
= {принят сигнал «точка»}.
Событие B = {принят сигнал «тире»}.
Гипотеза H
1
= {передан сигнал «точка»}.
Гипотеза H
2
= {передан сигнал «тире»}.
Событие А/H
1
= {принимается сигнал «точка», если передан сигнал
«точка»}.
Событие А/H
2
= {принимается сигнал «точка», если передан сигнал
«тире» (искажение сигнала «тире»)}.
Событие H
1
/A = {был передан сигнал «точка» при приёме сигнала
«точка»}.
Событие B/H
1
= {принимается сигнал «тире», если передан сигнал
«точка» (искажение сигнала «точка»)}.
Событие B/H
2
= {принимается сигнал «тире», если передан сигнал
«тире»}.
Событие H
2
/B = {был передан сигнал «тире» при приёме сигнала
«тире»}.
Априорные вероятности гипотез:
;
3
5
)(:)(
21
HPHP
12 1 2
53
() ()1 () ; ()
88
PH PH PH PH
.
Условные вероятности событий A и B
;
5
3
5
2
1)/(
1
HAP
2
1
(/ )
3
PAH
;
53 31 1
()
85 83 2
PA
.
;
5
2
)/(
1
HBP ;
3
2
3
1
1)/(
2
HBP
52 32 1
()
85 83 2
PB
.
Апостериорные вероятности гипотез:
;
4
3
2
1
5
3
8
5
)(
)/()(
)/(
11
1
AP
HAPHP
AHP
.
2
1
2
1
3
2
8
3
)(
)/()(
)/(
22
2
BP
HBPHP
BHP
32
Полученные вероятности могут рассматриваться как апостериорные
вероятности правильного приёма сигналов «точка» и «тире» соответствен-
но.
2. Случайные величины
[1, разд. 3.1, 3.2, с.28 - 42]
Законом распределения вероятностей случайной величины называ-
ется любое правило (таблица, функция), позволяющее находить вероятно-
сти всех возможных событий, связанных со случайной величиной. Суще-
ствуют две формы задания закона распределения случайной величины. Об-
щей формой задания закона распределения, как для дискретных, так и для
непрерывных, случайных величин является функция распределения.
Функцией распределения случайной величины Х называется веро-
ятность того, что она примет значение меньше, чем заданное число х
}{)(
x
X
P
x
F
. (2.1)
Свойства функции распределения:
1.
)(
x
F
– неубывающая функция своего аргумента, т.е.
)()(
12
xFxF , если
12
xx .
2. ()0, ()1FF , 1)(0
x
F
.
3. Вероятность попадания на полуинтервал
)()(}{)},[{
F
F
X
P
X
P
. (2.2)
2.1. Дискретные случайные величины
[1, разд. 3.1.2, с..30 - 32]
Ряд распределения
Для того чтобы задать закон распределения дискретной случайной
величины, достаточно перечислить все ее возможные значения и соот-
ветствующие им вероятности. Это вторая форма закона распределения,
присущая только дискретным случайным величинам. Она оформляется в
виде
ряда распределения, представляющего собой таблицу, в верхней
строке которой
в порядке возрастания перечислены все возможные зна-
чения случайной величины X –
,..., , ,
21 n
xxx а в нижней – вероятности
этих значений
12
, , ... , .
n
p
pp
Нормировочное условие:
1
1
n
i
i
p
.
Числовые характеристики
Математическое ожидание )(
x
m – это среднее значение
случайной величины
33
n
i
iix
pxXMm
1
][ . (2.3)
Дисперсия есть математическое ожидание квадрата цен-
трированной случайной величины
. Является характеристикой рассея-
ния
случайной величины около ее математического ожидания
22
1
[] [( )] ( )
n
x
ixi
i
DX M X m x m p
=
2
2
x
Xm,
2
2
1
[]
n
ii
i
Xxp
. (2.4)
Среднеквадратическое отклонение случайной величины
xx
DX ][
. (2.5)
Задача 2.1
Производятся последовательные независимые испытания пяти прибо-
ров на надежность. Каждый следующий прибор испытывается только в том
случае, если предыдущий оказался надежным.
Построить ряд распределения случайного числа испытанных прибо-
ров, если вероятность выдержать испытание для каждого из них равна 0,9
(дискретная случайная величина X – число приборов, прошедших испыта-
ние). Найти математическое ожидание
, дисперсию и среднеквадратическое
отклонение случайной величины X.
Решение задачи
p = 0,9; q = 0,1.
1
{1} 0,1;pPX q
2
{2} 0,90,10,09;pPX pq
22
3
{3} 0,90,10,081;pPX pq
33
4
{4} 0,90,10,073;pPX pq
4
5
1
{ 5} 1 0,656.
i
i
pPX p
Ряд распределения случайной величины X представлен табл. 2.1.
Числовые характеристики вычисляются по формулам (2.3) – (2.5).
;1,4656,05073,04081,0309,021,01
5
1
i
iix
pxm
5
222222
2
1
1 0,1 2 0,09 3 0,081 4 0,073 5 0,656 18, 66
ii
i
xp
.
;85,11,466,18
2
2
2
xx
mD
1,85 1,36.
xx
D
Таблица 2.1
x
i
1 2 3 4 5
p
i
0,100 0,090 0,081 0,073 0,656
34
Задача 2.2
Электронная аппаратура имеет три параллельные дублирующие ли-
нии. Вероятность выхода из строя каждой линии за время гарантированной
работы аппаратуры равна 0,1. Построить ряд распределения случайной ве-
личины Х, если Х – число линий, вышедших из строя. Найти числовые ха-
рактеристики этого распределения.
Решение задачи
Условия задачи соответствуют частной теореме повторения опытов,
следовательно, случайная величина X имеет биномиальное распределение с
параметрами: n = 3; p = 0,1; q = 0,9.
Случайная величина Х принима-
ет значения 0, 1, 2, 3. Вероятности p
i
этих значений вычисляются по формуле
Бернулли (1.3).
33
0
{0} 0,90,730;pPX p
112 2
13
{ 1} 3 0,1 0,9 0, 243;pPX С pq
22 2
23
{ 2} 3 0,1 0,9 0, 027;pPX Cpq
33
3
{ 3} 0,1 0,001pPX p
.
Нормировочное условие выполня-
ется.
Ряд распределения представлен в
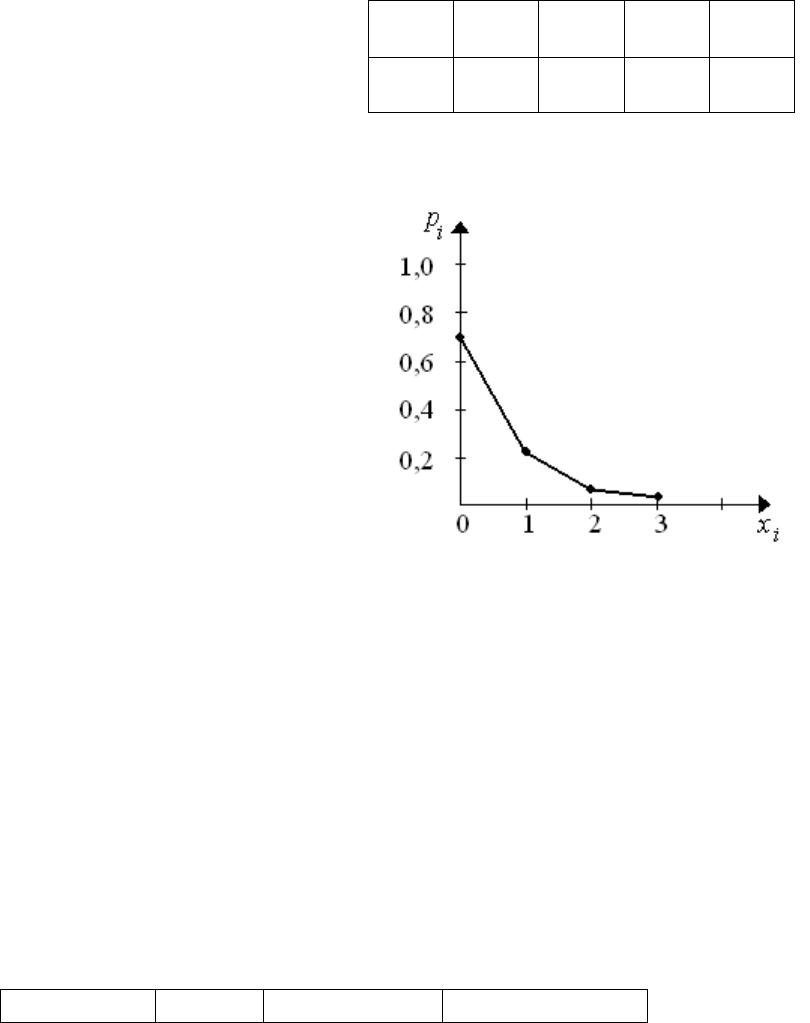
табл. 2.2, на рис. 2.1 изображен много-
угольник распределения случайной вели-
чины X.
Числовые характеристики распре-
деления:
2
0,3; 0,36; 0, 27
x
x
mD
;
0,52
x
.
Задача 2.3
В партии из 6 деталей 4 детали стандартные. Наудачу отобраны 3 де-
тали. Х – число стандартных деталей среди отобранных. Построить ряд и
многоугольник распределения. Найти числовые характеристики.
Решение задачи
Вероятности p
i
вычисляются по формуле (1.2). Необходимые для это-
го данные приведены в табл. 2.3.
Таблица 2.2
x
i
0 1 2 3
p
i
0,730 0,243 0,027 0,001
Таблица 2.3
Всего Стандартные Нестандартные
Рис. 2.1
35
0
{0}0pPX
(нестандартных деталей в партии только две);
12
42
1
3
6
41
{1} ;
20 5
CC
pPX
C
21
42
2
3
6
12 3
{2} ;
20 5
CC
pPX
C
30
42
3
3
6
41 1
{3}
20 5
CC
pPX
C
.
Нормировочное условие выпол-
няется.
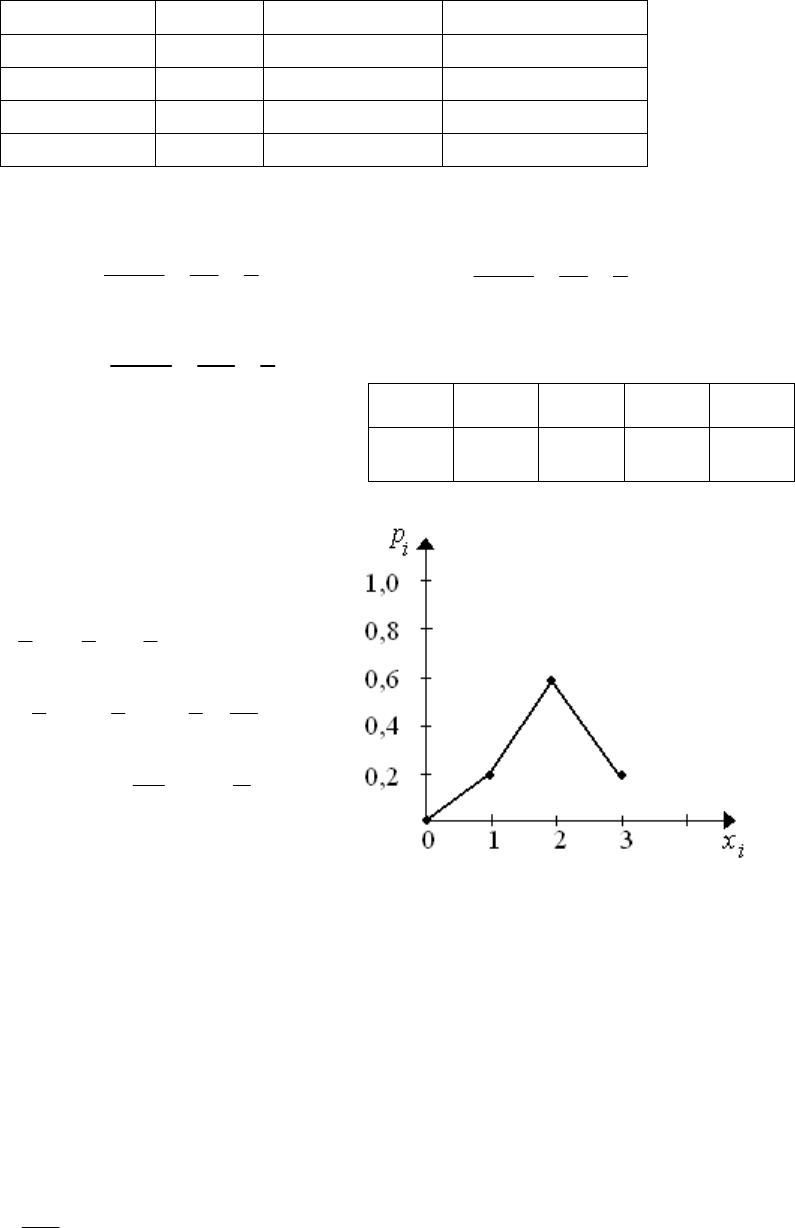
Ряд распределения представлен в
табл. 2.4, на рис. 2.2 изображен много-
угольник распределения случайной
величины X.
;2
5
1
3
5
3
2
5
1
1
x
m
;
5
22
5
1
3
5
3
2
5
1
1
222
2
2
2
22 2
4
55
xx
Dm ;
0,63
x
.
2.2. Непрерывные случайные величины
[1, разд. 3.1.3, с. 32-35]
Законы распределения
Производная от функции распределения называется плотностью
распределения вероятностей f(x) или дифференциальным законом рас-
пределения
случайной величины Х:
()
dF
fx
dx
. (2.6)
Это вторая форма закона распределения непрерывной случайной ве-
личины. Ф
ункция распределения при этом называется ещё и интеграль-
ным законом распределения
, поскольку
Партия 6 4 2
Выборка 0 3 х = 0 3?
Выборка 1 3 х = 1 2
Выборка 2 3 х = 2 1
Выборка 3 3 х = 3 0
Таблица 2.4
x
i
0 1 2 3
p
i
0 0,2 0,6 0,2
Рис. 2.2
36
x
dxxfxXPxXPxF )(}{}{)( . (2.7)
Нормировочные условия для функции и плотности распределения
имеют вид
() 1F ,
.1)( dxxf (2.8)
Вероятность попадания на интервал (α, β)
dxxfXP
)(}{
= ( ) ( )FF
. (2.9)
Числовые характеристики
dxxxfXMm
x
)(][ , (2.10)
2
2
2
x
x
DX x m f xdx X m
, (2.11)
2
2
Xxfxdx
.
xx
DX ][
.
Задача 2.4
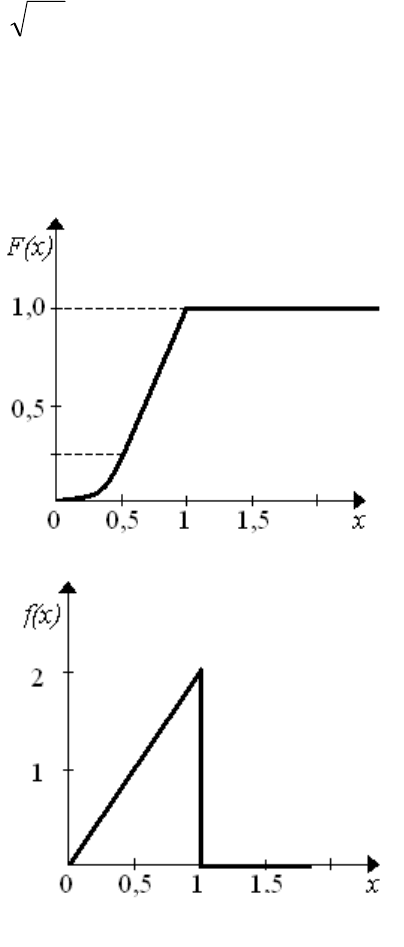
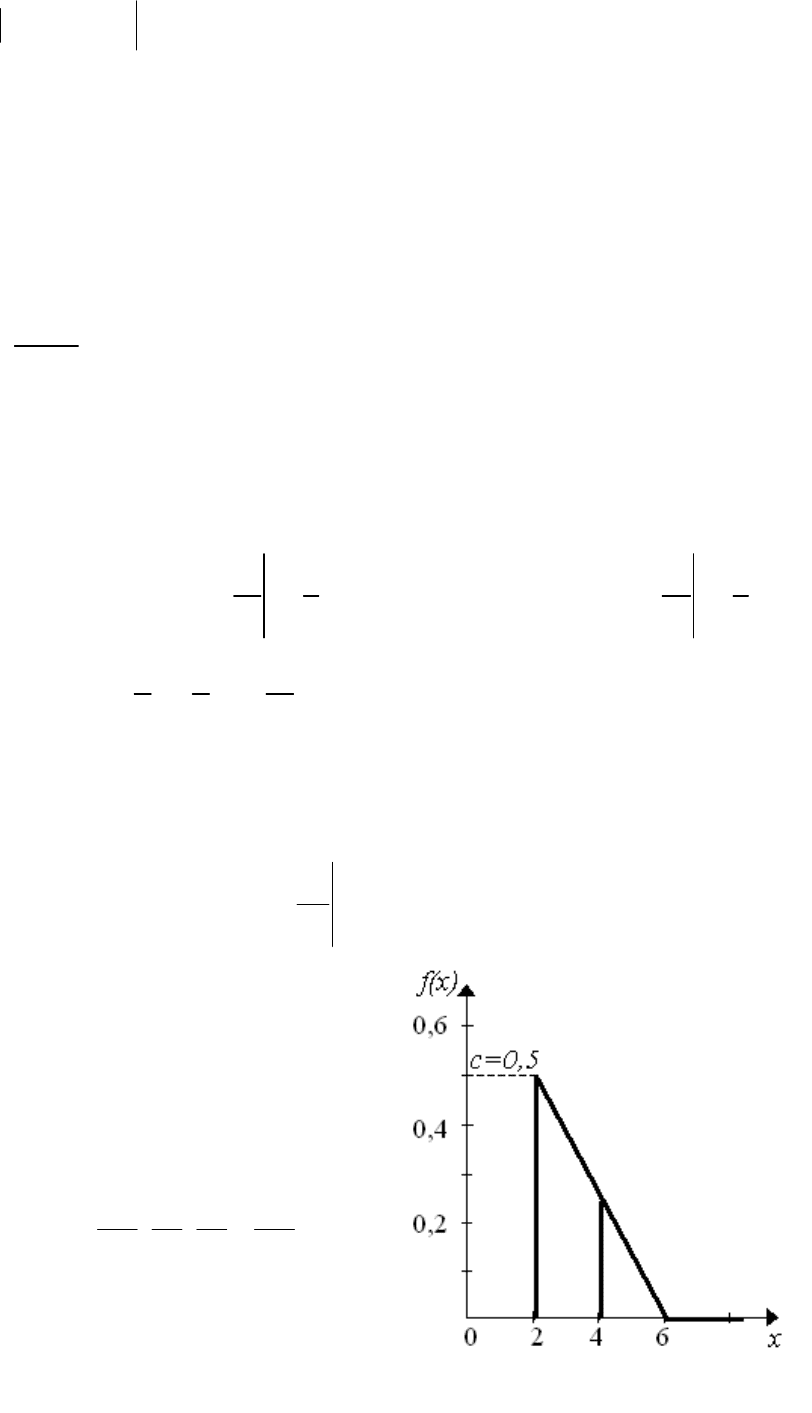
Закон распределения случайной величины Х задан функцией распре-
деления F(х) =
2
, (0,1)ax x . Найти:
1. Значение параметра а.
2. Построить графики характери-
стик функций F(x) и f(x).
3. Найти числовые характеристики
x
m и
x
D .
4. Найти вероятность того, что в ре-
зультате четырех испытаний случайная
величина Х дважды примет значение,
принадлежащее интервалу (0; 0,5).
Решение задачи
1. Значение параметра a опре-
деляется условием нормировки (2.8):
Рис. 2.3
Рис. 2.4
37
2
1
1
( ) 1; 1; 1
x
x
Fx ax a
.
2.
Функция распределения F(х) представлена на рис 2.3.
2
0, 0,
() , 0 1,
1, 1.
x
Fx x x
x
Плотность распределения вероятностей f(x) определяется в соот-
ветствии с выражением (2.6). Её график изображен на рис. 2.4.
()
() 2.
dF x
f
xx
dx
0, 0,
() 2, 0 1,
0, 1.
x
fx x x
x
3.
Числовые характеристики (формулы (2.10), (2.11)):
1
11
3
2
00
0
2
() 2 2 ;
33
x
x
mxfxdxxdx
1
11
4
23
2
00
0
1
() 2 2 ;
42
x
xfxdx xdx
2
2
2
12 1
.
23 18
xx
Dm
4.
P – вероятность попадания на интервал (0; 0,5) вычисляется
двумя способами (см. формулы (2.9)):
2
a) (0,5) (0) 0,5 0,25PF F;
0,5
0,5 0,5
2
00
0
b
) ( ) 2 2 0,25
2
x
Pfxdx xdx
.
Вероятность того, что в результате
четырех испытаний случайная величина Х
дважды примет значение, принадлежащее
интервалу (0; 0,5) вычисляется по формуле
Бернулли (1.3).
4; 2; 0,25; 1 0,75nmp qp ,
.21,0
4
96
4
3
4
1
21
34
42
2
2
222
44,2
qpCP
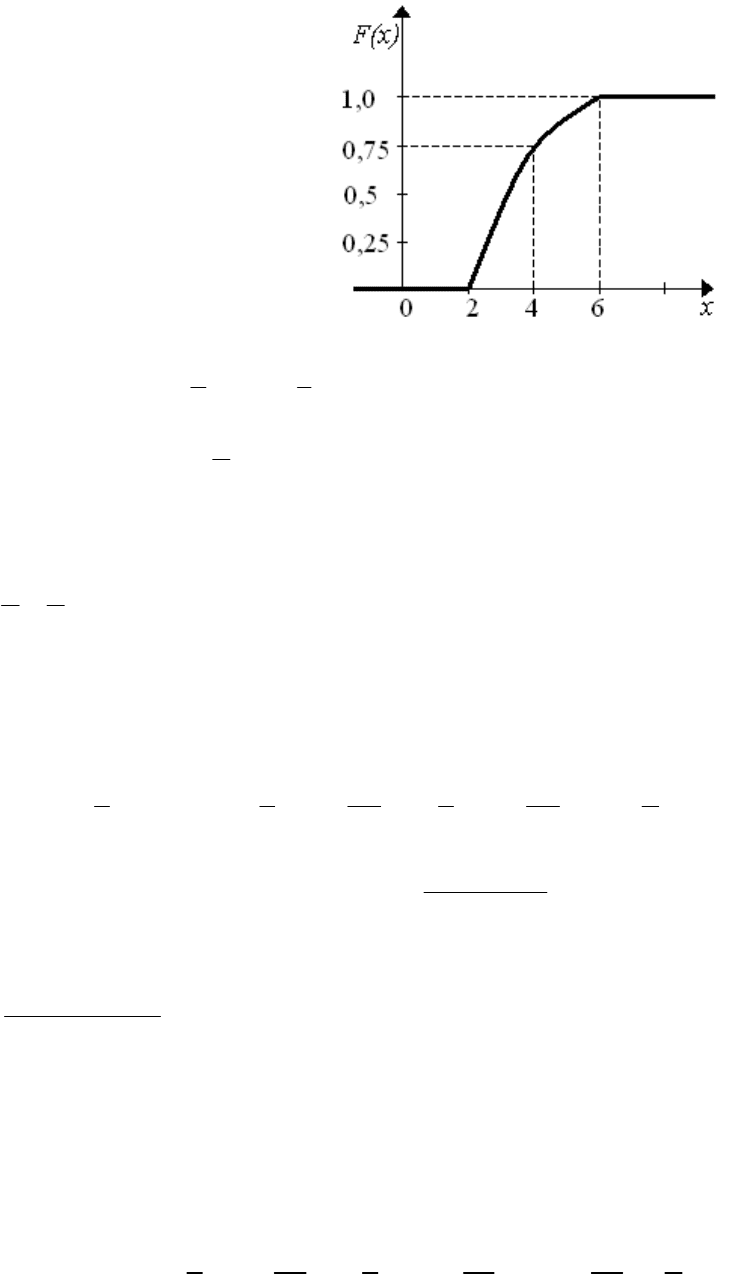
Задача 2.5
На рис. 2.5 приведен график плотно-
сти распределения случайной величины Х.
Найти математические выражения
Рис. 2.5
38
для функций f(x) и F(x) и построить гра-
фик функции F(x). Определить вероят-
ность попадания случайной величины Х
на интервал (4; 6).
Решение задачи
( ) ; 0,5; , , ?
f
xaxb c ab
Используя значения функции f(x)
при x = 2 и x = 6, получим два уравнения
относительно переменных a и b.
11
1. (2) 2 0,5 2 6 ; ;
28
fab aaa
3
2. (6) 6 0 6
4
fab ba.
Таким образом,
0, 2,
3
() , 2 6,
84
0, 6.
x
x
fx x
x
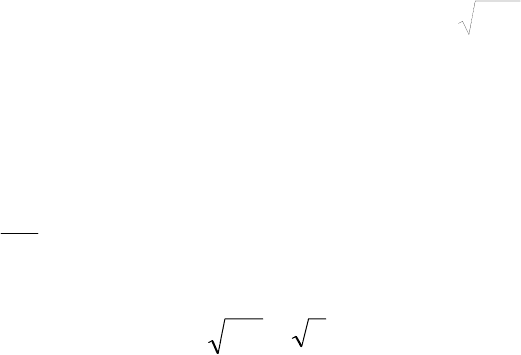
В соответствии с выражением (2.7) определяется функция распреде-
ления F(x), график её представлен на рис. 2.6.
x
x
x
x
x
x
xdxxdxxfxF
2
2
2
2
2
;
2
4
12
2
6
8
1
2
6
8
1
)6(
8
1
)()(
Условие нормировки выполняется:
36 72 20
(6) 1
16
F
.
.6 ,1
,62 ,
16
2012
,2 ,0
)(
2
x
x
xx
x
xF
Вероятность попадания случайной величины X на интервал (4, 6)
определена двумя способами:
{4 6} (6) (4) 1 0, 75 0, 25;PX F F
6
6
22
4
4
113641
{4 6} ( ) 6 6 6 6 4 .
828 2 24
x
PX fxdx x
Рис. 2.6
39
5. Наиболее часто встречающиеся законы рас-
пределения случайных величин
3.1. Биномиальное распределение. Распределение Пуассона
[1, разд. 3.3.1, с. 43 – 49]
Дискретная случайная величина X имеет биномиальное распреде-
ление
, если она может принимать значения 0, 1, 2, …, n, а соответству-
ющие им вероятности вычисляются согласно формуле
Бернулли (1.3)
,
{ } , 0 1, 1 , 0, 1, ..., .
mmnm
mmn n
p
PPXmCpq pq pm n
Числовые характеристики биномиального распределения:
npXMm
x
][
,
.σ npqnpq,XDD
xx
(3.1)
Случайная величина X имеет распределение Пуассона, если она
может принимать значения 0, 1, …, m,… (счетное множество значений), а
соответствующие этим значениям вероятности определяются формулой
!
m
a
m
a
Pe
m
, m=0, 1,… .
(3.2)
Числовые характеристики распределения Пуассона:
aDaDam
xxxx
, , . (3.3)
Распределение Пуассона является предельным для биномиального
распределения,
когда число опытов стремится к бесконечности (
n)
и одновременно вероятность p бесконечно уменьшается до нуля (
0
p
),
но так, что их произведение сохраняется в пределе постоянным
anp
p
n
lim
0
.
Простейший или стационарный пуассоновский поток. Интенсив-
ность потока – с
реднее число событий λ, появляющихся в единицу време-
ни.
Случайная величина X – число точек, попадающих на участок времени
протяженностью τ,
имеет распределение Пуассона с параметром
a.
Задача 3.1
В ячейку памяти ЭВМ записывает 8-разрядное двоичное число. Зна-
чение «0» и «1» в каждом разряде появляется с равной вероятностью. Слу-
чайная величина
Х – число единиц в записи двоичного числа. Найти веро-
ятность событий:
А = {Х = 4}; В = {X > 4}.

40
Решение задачи
Случайная величина Х имеет биномиальное распределение:
n = 8; p =0,5; q = 1 - p =0,5.
444 8
4,8 8
8765
() { 4} 0,5 0,27
1234
PA PX P C p q
,
8
8
5678
88888
5
1
( ) { 4} ( ) 0,36.
2
i
i
PB PX P C C C C
Задача 3.2
По каналу связи передается шесть сообщений. Каждое из них незави-
симо от других может быть искажено с вероятностью, равной 0,1.
Найти вероятности событий:
А = {искажены ровно три сообщения};
B = {искажено не менее трех сообщений};
С = {все сообщения будут переданы без искажения}.
Решение задачи
В рассматриваемой задаче случайная величина X (число переданных
сообщений с искажениями) имеет
биномиальное распределение.
n = 6; p = 0,1; q = 0,9.
Событие A. m=3.
3363 3 3
3,6 6
654
( ) 0,1 0,9 0, 015
123
PA P Cpq
.
Событие B. m > 3.
3,6 4,6 5,6 6,6 0,6 1,6 2,6
() 1 ( )
n
kknk
n
km
PB C pq P P P Ð Ð Ð Ð
.
;531,09,0
6600
66,0
qpCP ;354,09,01,06
5511
66,1
qpCP
;098,09,01,0
21
56
42422
66,2
qpCP
.017,0)(
B
P
Событие С. m=0.
.531,0)(
6,0
PCP
Задача 3.3
Устройство состоит из большого числа независимо работающих эле-
ментов с одинаковой, очень маленькой вероятностью отказа каждого эле-
мента за время
Т. Найти среднее число отказавших за время Т элементов,
