Рубин А.Б., Пытьева Н.Ф., Ризниченко Г.Ю. Кинетика биологических процессов

Подождите немного. Документ загружается.

главе. Пусть, например, в

результате

некоторого отклонения

(Да<0) от стационарной точки Oi величина а стала меньше ста-

ционарного

значения. В этой области (a<ai) скорость притока

субстрата больше скорости его расхода (производная —-— =

=/(а,0)>О,

см. рис.

III.9,

Л), следовательно,

будет

происходить

накопление

субстрата и переменная а

будет

самопроизвольно ра-

сти,

приближаясь к значению ai. Если же отклонение от стацио-

нарной

точки таково, что о

озмущ>(Т1(Д0>О), то в этом

случае

скорость расхода

'-, о) < О,

субстрата

рис.

Ш.9Л

больше скорости его притока

«возмущенная» величина

вновь

приближаясь к ста-

<Гвозмущ

будет

уменьшаться,

ционарному

значению ои Та-

ким

образом, состояние oi ус-

тойчиво.

Аналогичные рассуж-

дения

приводят к выводу о

том, что стационарная точка 0з

также устойчива, а 02 — неус-

тойчива. При

всех

значениях

управляющего параметра в ин-

тервале^ ^ос^аг] где аь осг

соответствуют бифуркацион-

ным

значениям параметра,

рассматриваемая система мо-

жет функционировать в одном

из

двух

устойчивых стацио-

нарных состояний. Как было

показано

в гл. 2 первой части

книги,

динамические системы

<с

такими характеристиками

обладают триггерными свойст-

вами.

Это означает, что при

изменении

управляющего па-

раметра наша система может

переключаться из одного устойчивого режима в другой. Поясним

с помощью графика, как происходит такое переключение.

Предположим, что исходному состоянию системы соответствует

стационарная

точка Л, лежащая на верхней ветви кривой в (а).

Будем понижать a — скорость притока субстрата, при этом систе-

ма начнет «перемещаться» влево вдоль верхней устойчивой ветви

стационарных состояний. При достижении бифуркационного зна-

чения

параметра «i система покинет неустойчивую точку В и, со-

вершив скачкообразный переход B-+D, попадет на нижнюю ветвь

устойчивых стационарных состояний. Увеличивая вновь значения

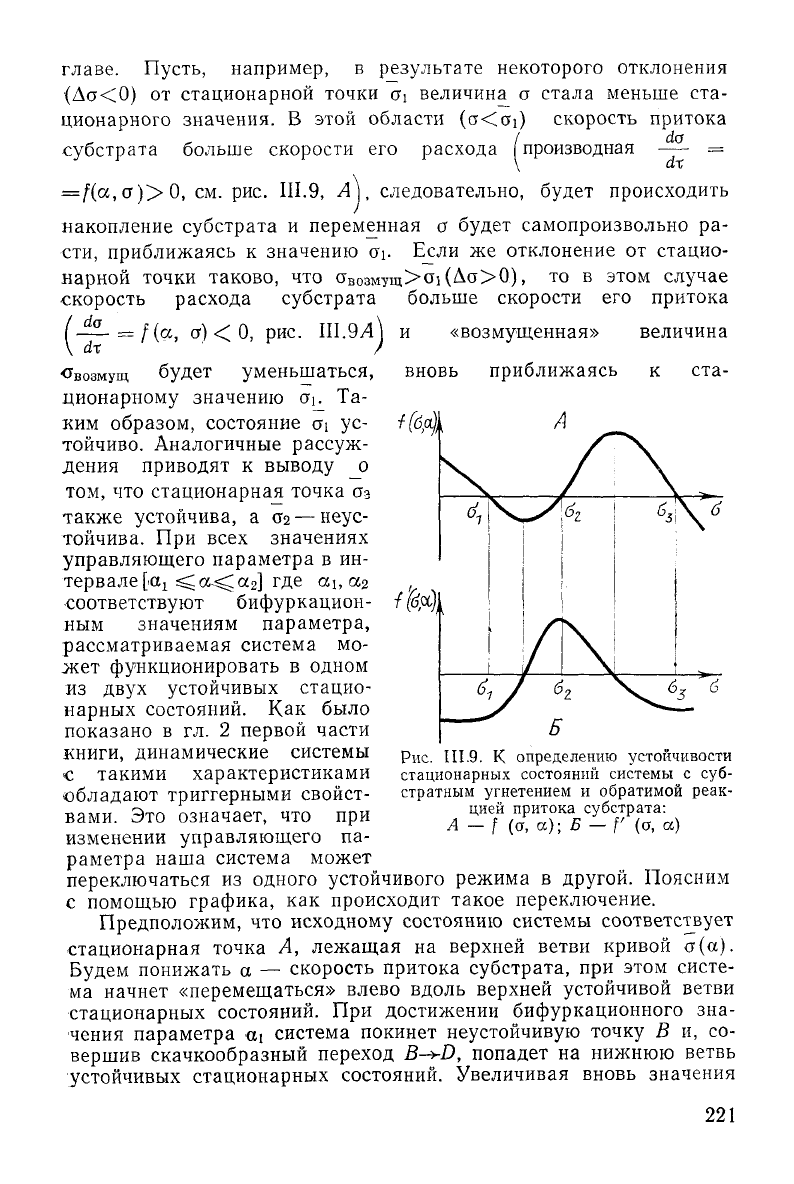
Рис.

Ш.9. К определению устойчивости

стационарных

состояний системы с суб-

стратным угнетением и обратимой реак-

цией

притока субстрата:

— f (о, а); Б — Г {а, а)

221

управляющего параметра от cti до аг, можно перевести систему

вдоль устойчивой ветви DC до бифуркационной точки (С), после

достижения которой система самопроизвольно вернется в исходное

состояние (А). При изменении управляющего параметра а (умень-

шении

и увеличении до прежних значений) осуществится замкну-

тый цикл состояний рассматриваемой системы.

Какое

из

двух

возможных устойчивых состояний реализуется в

системе и направление скачкообразных переходов зависит от того,

происходит уменьшение или увеличение параметра. Это свойство

Рис.

ШЛО. Явление гистерезиса в си-

стеме с субстратным угнетением и об-

ратимой реакцией притока

субстрата

Рис.

111.11. Характеристики реакции

с субстратным угнетением и обрати-

мой

реакцией притока

субстрата

в за-

висимости от параметра а (скорости

притока субстрата):

— скорость «источника» и фермен-

тативной реакции в зависимости от

концентрации

субстрата;

Б — ста-

ционарная

скорость ферментативной

реакции

как функция параметра а

систем — различными путями совершать переход из одного со-

стояния

другое

по

ходу

изменения параметра в сторону меньших

или

больших значений — названо гистерезисом. Рисунок ШЛО

иллюстрирует явление гистерезиса в системе (III.5—3) при изме-

нении

скорости притока субстрата.

До сих пор мы характеризовали систему величиной 0, отвечаю-

щей

стационарным концентрациям субстрата. На рис. 111.11, А, Б

показано,

как при изменении управляющего параметра а меняется

стационарная

скорость рассматриваемой реакции, т. е. стационар-

ная

скорость потребления субстрата v

v =

Легко видеть, что верхняя ОС и нижняя ВА ветви кривой и (а)

отвечает устойчивым, а промежуточный участок ВС — неустойчи-

вым стационарным состояниям системы. Заштрихованная область

соответствует петле гистерезиса, которую описывает система при

222

изменении

скорости притока субстрата как управляющего пара-

метра.

Заметим, что в рассматриваемом

случае

обратимой реакции

притока субстрата изменение параметра а является не единствен-

ным

способом управления системой. Величину р, характеризую-

щую скорость обратной реакции S->S

или реакции побочного

стока субстрата, также можно рассматривать как управляющий

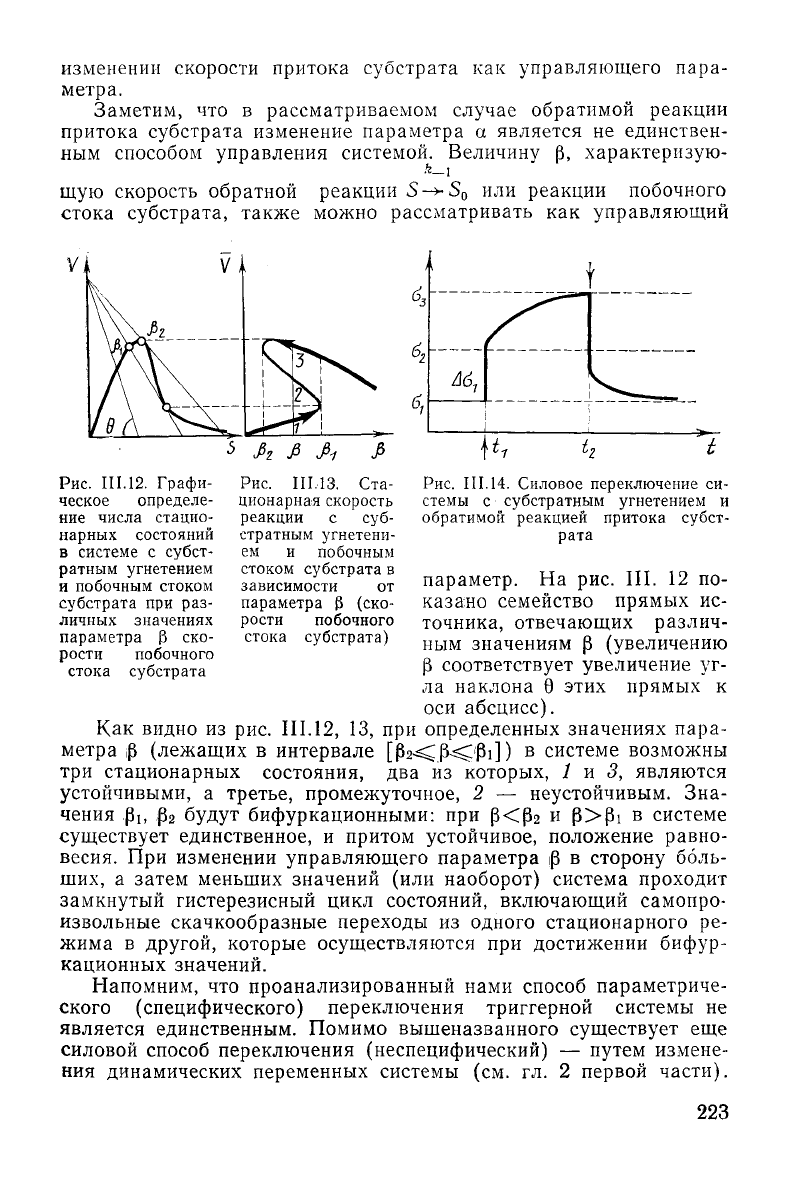
Рис.

III.12.

Графи-

ческое определе-

ние

числа стацио-

нарных состояний

системе с субст-

ратным угнетением

побочным стоком

субстрата при раз-

личных значениях

параметра 3 ско-

рости побочного

стока субстрата

Рис.

111,13. Ста-

ционарная

скорость

реакции

с суб-

стратным угнетени-

ем и побочным

стоком субстрата в

зависимости от

параметра 3 (ско-

рости побочного

стока субстрата)

Рис.

III.14.

Силовое переключение си-

стемы с субстратным угнетением и

обратимой реакцией притока субст-

рата

параметр. На рис. III. 12 по-

казано семейство прямых ис-

точника, отвечающих различ-

ным

значениям р (увеличению

р соответствует увеличение уг-

ла наклона 8 этих прямых к

оси абсцисс).

Как

видно из рис.

III.12,

13, при определенных значениях пара-

метра р (лежащих в интервале [fb^P-^'Pi]) в системе возможны

три стационарных состояния, два из которых, 1 и 3, являются

устойчивыми, а третье, промежуточное, 2 — неустойчивым. Зна-

чения

,р

будут

бифуркационными: при р<р2 и j3>Pi в системе

существует

единственное, и притом устойчивое, положение равно-

весия. При изменении управляющего параметра р в сторону боль-

ших, а затем меньших значений (или наоборот) система проходит

замкнутый гистерезисный цикл состояний, включающий самопро-

извольные скачкообразные переходы из одного стационарного ре-

жима в другой, которые осуществляются при достижении бифур-

кационных значений.

Напомним,

что проанализированный нами способ параметриче-

ского (специфического) переключения триггерной системы не

является единственным. Помимо вышеназванного

существует

еще

силовой способ переключения (неспецифический) — путем измене-

ния

динамических переменных системы (см. гл. 2 первой части).

223

Опишем

процесс силового переключения. Рассмотрим систему

(III.5—3)

при фиксированных значениях

всех

параметров, в том

числе

а=а*.

Пусть первоначально система находится в одном из

двух

устойчивых стационарных состояний cTj

(СМ.

рис.

III.8).

Если

результате

внешнего воздействия или флуктуации значение пере-

менной

а станет больше 02 (которое отвечает неустойчивому по-

ложению равновесия), система попадет в область влияния дру-

гого устойчивого состояния, самопроизвольно перейдет в это со-

стояние

будет

оставаться в нем до тех пор, пока новое внешнее

воздействие не уменьшит о до уровня ниже О2- Тогда система

вновь

попадет в область влияния исходного устойчивого положе-

ния

равновесия ai и совершит самопроизвольный переход в это со-

стояние.

Кинетика перехода описывается первым уравнением си-

стемы

(III.5—3).

При этом переменная а

ведет

себя во времени

примерно

так, как показано на рис.

III.14,

где t

— моменты

силового воздействия на систему.

Итак,

мы рассмотрели два примера открытых ферментативных

систем: реакцию с субстратным угнетением и постоянной скоро-

стью притока субстрата, а также реакцию с субстратным угнете-

нием

и обратимым процессом притока субстрата. На примере этих

реакций

мы продемонстрировали такие свойства динамических

систем, как множественность стационарных состояний, явление

гистерезиса, триггерные переключения. Указанное многообразие

свойств рассматриваемых динамических систем обусловлено, с од-

ной

стороны, их «открытостью», т. е. наличием потоков, обеспечи-

вающих обмен веществом с внешней средой, а с

другой

стороны,

существенной нелинейностью этих систем, обусловленной механиз-

мом субстратного угнетения. Благодаря этим факторам уравнение

ферментативной реакции становится — в

случае

постоянной ско-

рости притока субстрата — квадратичным, а в случае, если реак-

ция

притока субстрата обратима (или если имеется побочный

сток

субстрата), — кубическим

(III.5—4),

что, в свою очередь,

обусловливает возможность существования в системе

двух

или,

соответственно,

трех

стационарных состояний при фиксированных

значениях параметров. Сложно организованные ферментативные

системы

могут

обладать и большим числом стационарных состоя-

ний.

Так, авторы (Кхюгге,

Bergter,

Simon, 1975) рассмотрели мо-

дель ферментативного процесса, включающую две последователь-

ные

реакции с субстратным угнетением.

Анализ модели показал, что в такой системе в зависимости от

значений

ее параметров возможно существование от одного до

четырех устойчивых стационарных режимов.

В заключение

следует

отметить, что субстратное угнетение

активности фермента является очень распространенной, но не един-

ственной

причиной нелинейности ферментативных систем. Продукт

реакции

также может оказывать угнетающее (или активирующее)

действие на катализирующий ее фермент. В ферментативных си-

224

стемах с таким механизмом регулирования — по типу обратной

связи

— также возможно существование нескольких альтернатив-

ных стационарных состояний и наличие триггерных и гистерезис-

ных свойств. Более того, при определенных значениях параметров

открытых ферментативных системах «с обратной связью»

могут

возникать

устойчивые концентрационные колебания. Примеры

таких систем мы подробно рассмотрим в

главах

7, 8 настоящего

раздела.

Множественность стационарных состояний и связанные с нею

гистерезисные и триггерные явления

могут

играть весьма важную

роль как средства саморегулирования биологических систем. Дей-

ствительно, при наличии гистерезисных свойств поведение системы

ответ на изменение параметров, отражающее изменение внешних

условий, зависит от ее предыстории. Таким образом, свойственный

ферментативным системам гистерезис может являться основой

динамической памяти, присущей всем биологическим объектам.

В следующей главе мы рассмотрим примеры биологических

триггеров, важной составной частью которых являются фермента-

тивные системы.

Глава

ПРИМЕРЫ

БИОЛОГИЧЕСКИХ

ТРИГГЕРОВ

Триггерные свойства ферментативных систем совместно с фер-

ментобразующим аппаратом играют первостепенную роль в

регу-

лировании

внутриклеточных процессов метаболизма (см. модель

Жакоба и Моно, часть I, гл. 6), а также в процессах клеточной

дифференциации,

когда при делении появляются дочерние клет-

ки,

качественно отличные от клеток-предшественников. Кроме того,

настоящее время хорошо известны триггерные свойства фермен-

тативных систем, осуществляющих транспортную функцию. В част-

ности,

такие явления были обнаружены при изучении переноса

растворов электролитов через пористые мембраны.

В качестве примера биологического триггера рассмотрим не-

сколько

подробнее систему мембранного переноса, сопряженную с

химической реакцией, в которой

участвует

транспортируемое сое-

динение.

Предположим, что химический процесс катализируется фер-

ментом, свойства которого, в свою очередь, зависят от концентра-

ции

субстрата (транспортируемого вещества) или продукта реак-

ции.

Такая зависимость может быть основана на изменении кон-

формационного

состояния фермента при некоторых критических

концентрациях

названных соединений. В этих условиях вместе с

225

конформационным

состоянием фермента

будет

меняться и его ак-

тивность, а следовательно, и скорость химического процесса.

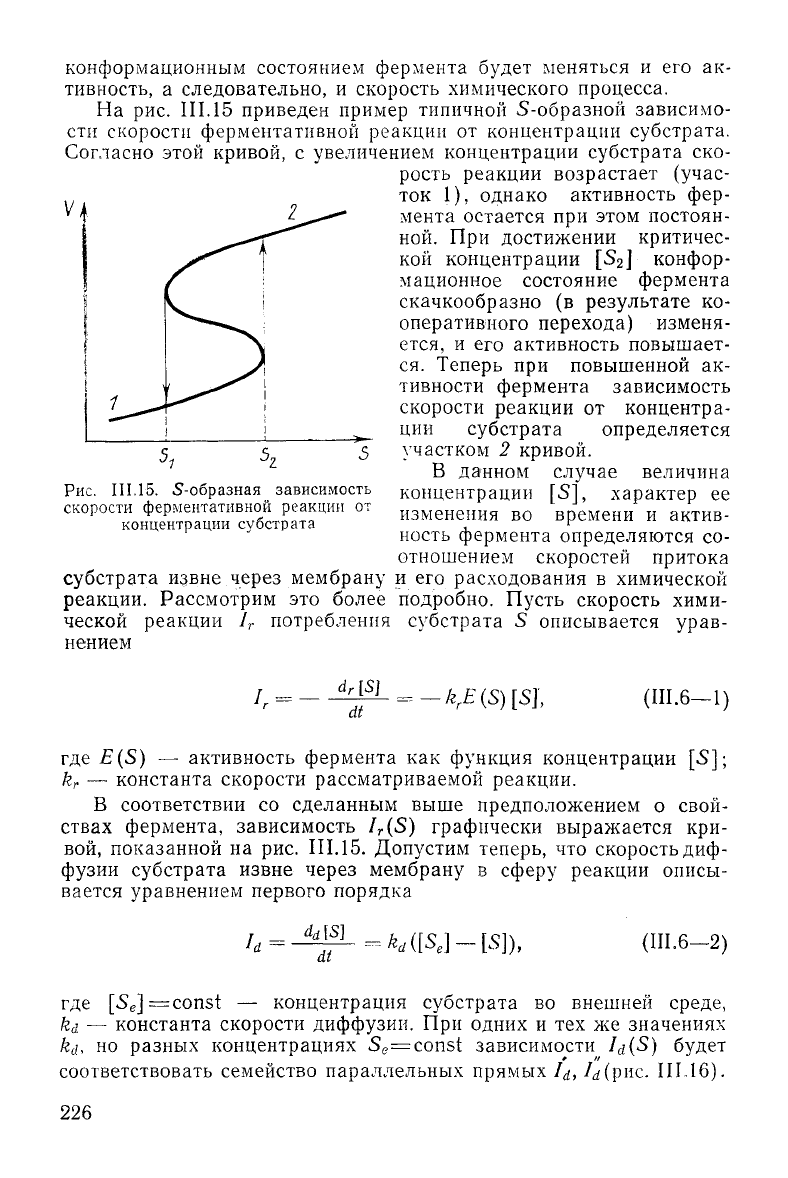
На

рис. III.15 приведен пример типичной 5-образной зависимо-

сти скорости ферментативной реакции от концентрации

субстрата.

Согласно этой кривой, с увеличением концентрации

субстрата

ско-

рость реакции возрастает (учас-

ток 1), однако активность фер-

мента остается при этом постоян-

ной.

При достижении критичес-

кой

концентрации [5

] конфор-

мационное состояние фермента

скачкообразно (в

результате

ко-

оперативного

перехода)

изменя-

ется, и его активность повышает-

ся.

Теперь при повышенной ак-

тивности фермента зависимость

скорости реакции от концентра-

ции

субстрата

определяется

участком 2 кривой.

В данном

случае

величина

концентрации

[S], характер ее

изменения

во времени и актив-

ность фермента определяются со-

Рис.

III.15.

5-образная зависимость

скорости ферментативной реакции от

концентрации

субстрата

отношением скоростей притока

субстрата

извне через мембрану и его расходования в химической

реакции.

Рассмотрим это более подробно. Пусть скорость хими-

ческой реакции /

потребления

субстрата

5 описывается урав-

нением

Л.

= —

[S]

=---k

E(S)[S],

(Ш.6—1)

где E(S) — активность фермента как функция концентрации [5];

—•

константа скорости рассматриваемой реакции.

В соответствии со сделанным выше предположением о свой-

ствах

фермента, зависимость I

(S) графически выражается кри-

вой,

показанной на рис.

III.15.

Допустим теперь, что скорость диф-

фузии

субстрата

извне через мембрану в сферу реакции описы-

вается уравнением первого порядка

Id =

\S]

(Ш.6—2)

где [5

]=const — концентрация

субстрата

во внешней среде,

kd — константа скорости диффузии. При одних и тех же значениях

ka,

но разных концентрациях 5

=const зависимости Id(S)

будет

соответствовать семейство параллельных прямых 1д, /<*(рис.

III.16).

226

Общее изменение [S] в

результате

двух

процессов описывается

уравнением

-^р-

= / (S) = I

(S) -

(S') = k

{{S

\ - [5]) - k

E (S) [S]. (III. 6-3)

В стационарном режиме скорости химической реакции и тран-

спорта субстрата через мембрану равны

между

собой. Найдем ста-

ционарные

решения уравнения (III.6—3) как точки пересечения

кривых /,.(5) и la(S'), в которых выполняется равенство

или

([S

] - [5]) = k

E (S) [S]. (III. 6-4)

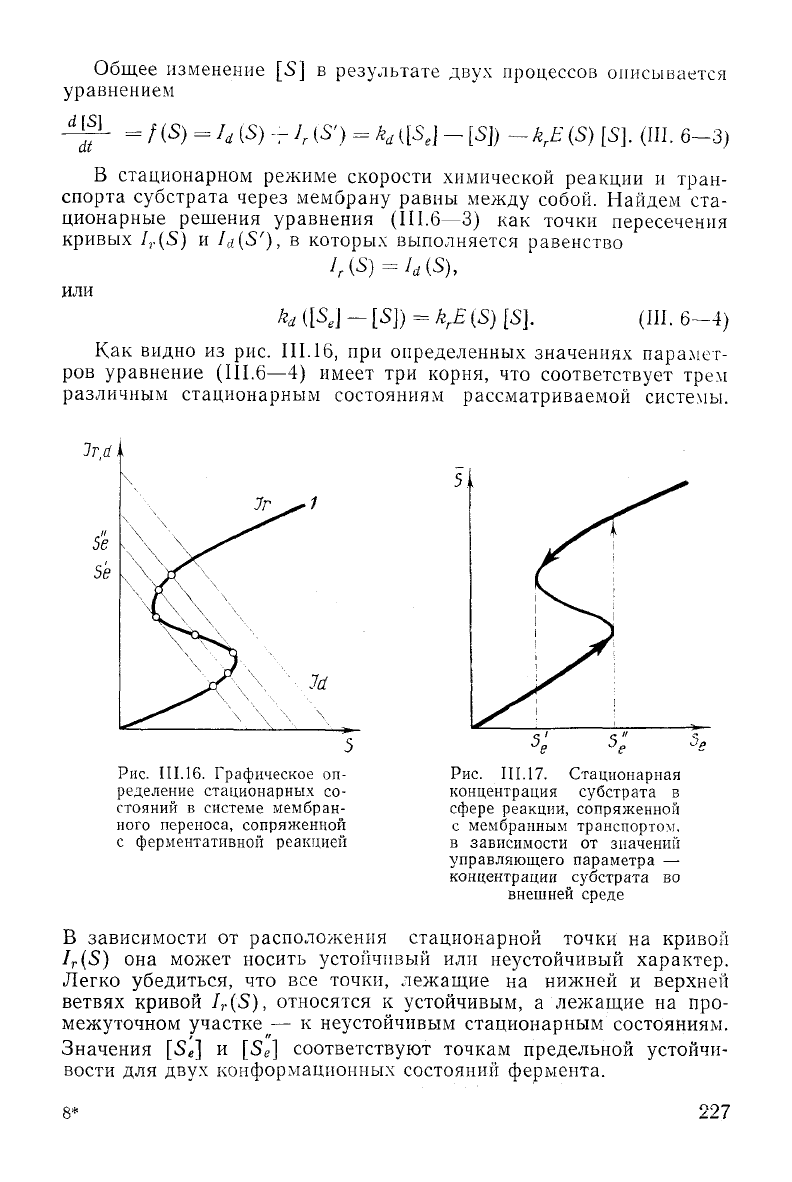
Как

видно из рис.

III.

16, при определенных значениях парамет-

ров уравнение (III.6—4) имеет три корня, что соответствует трем

различным стационарным состояниям рассматриваемой системы.

Jrd

Рис.

III.16. Графическое оп-

ределение стационарных со-

стояний

в системе мембран-

ного переноса, сопряженной

с ферментативной реакцией

Рис.

III.17. Стационарная

концентрация

субстрата

сфере реакции, сопряженной

с мембранным транспортом,

зависимости от значений

управляющего параметра —

концентрации

субстрата

во

внешней

среде

В зависимости от расположения стационарной точки на кривой

(S)

она может носить устойчивый или неустойчивый характер.

Легко убедиться, что все точки, лежащие на нижней и верхней

ветвях кривой

{S),

относятся к устойчивым, а лежащие на про-

межуточном участке — к неустойчивым стационарным состояниям.

Значения

] и [S

] соответствуют точкам предельной устойчи-

вости для

двух

конформационных состояний фермента.

227

Считая

концентрацию субстрата во внешней среде [S

] управ-

ляющим параметром, рассмотрим поведение нашей системы в

ответ на изменение этой величины. На рис. II 1.17 представлена

кривая

стационарных концентраций субстрата в сфере реакции в

зависимости от значений управляющего параметра [S

]. Легко

видеть, что по

ходу

изменения параметра в сторону меньших или

больших значений система описывает замкнутый гистерезисный

цикл

стационарных состояний, совершая скачкообразные триггер-

ные

переходы при достижении критических концентраций субстра-

та [S

], [S

], соответствующих точкам предельной устойчивости

конформационных

состояний фермента.

Рассматриваемая система обладает при определенных значе-

ниях

параметров способностью совершать релаксационные коле-

бания,

однако, прежде чем

перейти к обсуждению этого

явления,

рассмотрим еще

один

важный пример биоло-

гической системы, обладаю-

щей

несколькими стационар-

ными

состояниями и триггер-

ными

свойствами. Речь пойдет

процессах биосинтеза белка,

играющих, как известно, клю-

Ген

регулятор

Рис.

III.18.

Упрощенная схема

цессов

биосинтеза белка

про-

чевую

роль в развитии и диф-

ференциации

клеток.

Очевидно, функционирование системы биосинтеза белка в разных

стационарных режимах и наличие у нее триггерных свойств яв-

ляется фактором, обеспечивающим возможность регулирования

клеточным метаболизмом. В литературе

существует

несколько

триггерных моделей ферментообразующих систем (Чернавский

др., 1967; Баблоянц, Николис,

1971),

основанных на

схеме

Жако-

ба и Моно (1961). Не занимаясь подробно сравнительным анали-

зом триггерных свойств предложенных моделей, мы рассмотрим

лишь

некоторые свойства кинетической схемы биосинтеза белка,

следуя в основном работе Лавенды (Lavenda, 1972).

Последовательность процессов биосинтеза белка, согласно

Жакобу и Моно, схематически представлена на рис. II 1.18, где

объединены три категории процессов:

1) синтез mPHK (R); 2) синтез фермента Е; 3) метаболиче-

ская

реакция образования продукта х.

Синтез

mPHK, или процесс транскрипции, происходит на

участ-

ке

структурного гена ОГ и находится под контролем репрессора

у,

который синтезируется геном-регулятором и может блокировать

синтез mPHK, действуя на участок структурного гена, называемый

оператором ОП.

Если

синтез mPHK не заблокирован, то на образованной

отРНК

происходит процесс трансляции, или возникновение из ами-

нокислот

ферментной структуры Е. Фермент взаимодействует с

228

субстратом S, что приводит к образованию метаболита х. Репрес-

сор у может существовать в

двух

формах: активной а и неактив-

ной

Ь (рис.

III.18).

В активном состоянии у способен репресси-

ровать синтез

тРНК,

воздействуя на оператор структурного гена,

а в неактивном состоянии такого репрессирования не происходит.

Соотношение

между

активным а и неактивным b состояниями на-

ходится под влиянием метаболита х. В данном

случае

будем

счи-

тать, что под влиянием х репрессор у переходит в неактивное со-

стояние Ь, в

результате

чего подавление синтеза

тРНК

становится

невозможным. Процесс связывания молекул метаболита х моле-

кулой репрессора у не является одноактным, поскольку молекула

репрессора имеет несколько связывающих участков.

кинетической точки зрения процессы транскрипции, транс-

ляции

и образования метаболитов обладают существенно разными

характерными временами, что позволяет применить к рассматри-

ваемой

схеме

(рис. III.18) метод квазистационарных концентра-

ций.

Наиболее медленной стадией в процессе синтеза

тРНК

яв-

ляется образование комплекса репрессор — метаболит (ух{), где

— число молекул метаболита, связанных одной молекулой ре-

прессора. Несложный расчет показывает, что среднее число v мо-

лекул метаболита х, находящихся в комплексе с одной молекулой

репрессора у,

будет

равно

где ki — константа равновесия реакции образования комплекса

(III.

6—6)

Полагая L

= k

,...,ki, найдем, что

v=^

. (III. 6-7)

[=0

= 1.

Скорость синтеза

тРНК

пропорциональна числу v, так как по-

следнее определяет количество неактивных форм репрессора у.

Схеме, показанной на рис.

III.

18,

соответствуют

следующие

кинетические уравнения:

= г,К-г

£, (2) (III. 6-8)

229

JjL

= r

£E-r

, (3)

гь Гц, i's — константы скоростей

расхода

R, Е, х; г

, г

— кон-

станты скоростей синтеза R, Е, х. Поскольку узким местом являет-

ся

связывание х и у (изменение величины v), то вторая и третья

реакции

в системе (III.6—8) протекают намного скорее, чем пер-

вая

реакция синтеза

тРНК-

Это позволяет заменить переменные

величины E(t) и x[t) их стационарными значениями Е, х, которые

устанавливаются в системе в то время, как величина R еще про-

должает

изменяться. Приравняв к

нулю

вторые два уравнения в

(III.6—8),

найдем квазистационарную величину R =

—.

Подставим последнее выражение в первое уравнение (III.6—8) и.

ограничиваясь

случаем

п=3, получим окончательно

(III.

6-9)

где

a = I^S. (III. 6-10)

Уравнение (III.6—9) выражает зависимость скорости изменения

концентрации

тРНК от процессов ее синтеза

?щ>{х)

и распада

/от(^)-

Стационарные значения концентрации метаболита х опре-

деляются алгебраическим уравнением третьей степени

/ (J, ее) = х

— fЗа — -^-)х

-L (L

— 2L,a) LJ

x— (aL

— 1)Ц'

= 0.

(III.

6—11)

Корни

этого уравнения

Х\, х

, х

можно найти

как

точки пересе-

чения

графиков функций притока fnp(*)

оттока

от

(^),

стоящих

в правой части (III.6—9),

где

Кривая

зависимости I

i(x) представляет собой прямую, парал-

лельную

оси абсцисс и пересекающую кубическую кривую

1щ>{х)

точках с координатами Х\, х

, х

. Характер устойчивости стацио-

нарных точек Х\, х

, лг

легко определить по знаку производной

правой

части уравнения

(III.6—9).

Очевидно,

230