Рубин А.Б., Пытьева Н.Ф., Ризниченко Г.Ю. Кинетика биологических процессов

Подождите немного. Документ загружается.

время алгоритм основан на применении теории графов

(Берж,

1962; Бессонов, 1964). Подробное описание этого метода выходит

за рамки нашего изложения, необходимую информацию читатель

может найти в соответствующей литературе (Темкин, 1963, 1965;

Волькенштейн, 1966, 1975).

Глава

КВАЗИСТАЦИОНАРНЫЙ

АНАЛИЗ

ОТКРЫТЫХ

ФЕРМЕНТАТИВНЫХ

СИСТЕМ

Свойственная

биологическим системам временная иерархия с

вытекающим из нее эффектом строгого узкого места является

обстоятельством, благодаря которому число независимых перемен-

ных в модели, как и в реальном объекте, оказывается существен-

но

меньше числа промежуточных стадий процесса. Как мы увидим

дальнейшем, большинство успешных моделей ферментативных

систем содержит два или три уравнения. Ниже мы подробно оста-

новимся

на

«технологии»

построения и анализа таких моделей.

Для анализа систем, в которых, наряду с быстрыми процес-

сами,

имеют место медленные изменения отдельных компонентов,

используется метод квазистационарных концентраций

(КСК),

о ко-

тором уже шла речь в гл. 9 первой части книги. Строгое обосно-

вание этого метода базируется на теореме Тихонова, содержание

границы применимости которой изложены там же. В настоящей

главе мы остановимся на отдельных важных этапах применения

метода КСК: покажем необходимость приведения динамической

системы к безразмерному

виду,

проведем операцию выделения ма-

лого параметра и процедуру упрощения исходной системы диффе-

ренциальных уравнений. Сформулировав окончательную модель,

подробно проанализируем ее стационарные характеристики. В ка-

честве примеров рассмотрим ферментативные системы, в которых

реализуются такие интересные с общетеоретической и практиче-

ской

точек зрения свойства, как множественные стационарные со-

стояния,

явления гистерезиса, триггерные свойства и способность

переключениям. Таким образом, эти примеры

будут

служить

иллюстрацией к тому разделу книги, где были введены соответ-

ствующие понятия (см. часть I, гл. 6).

Итак,

рассмотрим открытую ферментативную систему с суб-

стратным угнетением и постоянной скоростью «источника», т. е.

с постоянной скоростью притока субстрата в сферу реакции

* Графом в

математике

называется топологическая

схема,

построенная из

узло-

вых точек и соединяющих их линий.

211

S£+S^S

£;

pX. (Ш.4—2)

*-4

Обратную реакцию E + P-+SE можно не учитывать, так как обыч-

но

она протекает с крайне низкой скоростью.

Запишем

соответствующую

схеме

(II

1.4—2)

систему кинетиче-

ских уравнений

К [S] [E] - k-

[SE] - k

[SE] - k, [SE] [S] + £_

E];

^If- =

-k

[S][E]

-rk^[SE]

[SE];

(П1.4-3)

d[p]

[SE]-k

[P].

Учтем,

прежде всего, условие сохранения числа свободных и

связанных в комплексах молекул фермента

[Е] + [SE] + [&Е] = е

(III.4-4)

благодаря которому систему (II

1.4—3)

можно несколько упро-

стить, заменив дифференциальное уравнение для (Е) алгебраиче-

ским

равенством (Ш.4—4). Произведя соответствующую замену

переменных Е =

—[SE]

— [5

£], первые три уравнения (Ш.4—3)

можно привести к виду

= kx {

] - k, [S] (e

- [SE] -

[S*E])

+ k-

[SE] -

h [S] (e

- [SE] - [&E]) - k_

[SE] - k, [SE] -

(III.4—5)

Заметим,

что уравнения (Ш.4—5) не содержат переменной Р.

Следовательно, кинетика процесса накопления продукта (так на-

зываемого ведомого процесса) целиком определяется решением

системы (Ш.4—5).

212

Аналитическое исследование системы (III.4—5) весьма

затруд-

нительно.

Посмотрим поэтому, допускает ли она упрощение с по-

мощью метода квазистационарных концентраций. С этой целью

сравним

между

собой

«быстроту»

изменения отдельных перемен-

ных.

Примем,

что концентрации реагентов выражены в молях на

литр,

время — в секундах. Легко заметить, что параметры рас-

сматриваемой системы (III.4—5)—&i, kz, &-2, &-4 и k

, k\ имеют

разную размерность: с"

и (с/моль/л)"

соответственно. Это обус-

ловлено тем обстоятельством, что первая группа констант харак-

теризует скорость

мономолекулярных

процессов притока субстрата

распада комплексов SE и S

E, а параметры k

, k\ отвечают би-

молекулярным,

реакциям образования активного и неактивного

фермент-субстратных комплексов. Очевидно, параметры, характе-

ризующие различные по природе процессы, нельзя сравнивать

между

собой по величине. Кроме того, скорость рассматриваемых

реакций

определяется не только соответствующими кинетическими

константами,

но и концентрациями реагирующих веществ, кото-

рые,

в свою очередь,

могут

различаться весьма значительно. В си-

лу этих обстоятельств нельзя оценить скорость изменения пере-

менных системы и решить вопрос о том, какие из них являются

быстрыми, а какие медленными, исходя из

размерных

констант

скоростей.

Приведем систему (Ш.4—5) к безразмерному

виду.

Это можно

сделать несколькими способами, поскольку универсальных рецеп-

тов «обезразмеривания» не

существует.

В качестве характерных

масштабов можно выбрать, например, исходные концентрации суб-

страта [S

] и фермента е

. Однако в данном

случае

удобнее вве-

сти следующие безразмерные концентрации:

&_2 + *3

где

= г —

константа Михаэлиса,

время

т =

t/K

Напомним,

что величина Кт соответствует концентрации суб-

страта, при которой половина молекул фермента находится в со-

стоянии

комплекса Михаэлиса. Обычно концентрации субстрата и

продукта имеют величину порядка Кт, следовательно, при таком

выборе масштабных множителей переменные а, р, х и у — порядка

единицы.

213

Запишем

систему (Ш.4—5) в новых переменных

dx k

*' Й

ft,

^ AL = AR ax - -i=L y. (III.4-7)

dx k

Введем следующие обозначения безразмерных кинетических

параметров системы (Ш.4—7):

„

_ fei[5o] . - _. к* [So] . ,

kdSp]

Величина е = является малым параметром. Действительно,

концентрация

фермента всегда на несколько порядков ниже кон-

центрации

субстрата, которая, в свою очередь, обычно бывает

одного порядка с величиной /С

~ Ю~

, так что

е~10~

10~

Согласно теореме Тихонова, наличие малого параметра s перед

соответствующими производными означает, что концентрации фер-

мент-субстратного комплекса [SE] и неактивного комплекса [S

являются быстрыми переменными.

Следует

отметить, что

«быст-

рота»

этих переменных обеспечивается существенным различием

концентраций

реагентов (субстрата и фермента), а не расхожде-

нием

кинетических констант рассматриваемых реакций.

Таким

образом, используя введенные выше обозначения

(Ш.4—8),

систему (Ш.4—7) можно записать в каноническом

виде

•— = а — аа (1 — х —у) — box — сх + dy,

е = аа (1 — х — у) — Ьах — х + dy = X, (а)

е —

— = box — du = Y. (6)

dx '

(III.4—9)

В соответствии с терминологией Тихонова

будем

рассматри-

вать первое уравнение системы (Ш.4—9) как вырожденное, а два

214

последних

—

как

присоединенную систему. Нетрудно убедиться,

что

особая точка присоединенной системы устойчива

и,

следовательно,

условия применимости теоремы Тихонова выполнены.

Заметим,

что

уравнения (II

1.4—9а,

б)

линейны

по х и у (а при

этом считаем параметром). Характеристические показатели этой

системы определяются уравнением

где

дХ

, дУ \ . I дХ дУ дХ дУ

дх

ду ) \ дх ду ду дх

Согласно этому уравнению,

знак

действительной части

и, сле-

довательно, характер устойчивости особых точек присоединенной

системы зависят

от

того, каков

знак

величины

В. А

именно,

осо-

бая точка устойчива, если

5<0.

Легко видеть,

что в

нашем

случае

величина

= — o{a +

— d— 1

отрицательна

при

любых

значениях параметров

a, b, d и ст, так

как

последние,

по

определению,

всегда

положительны.

Итак,

особая точка присоединенной системы устойчива

и, сле-

довательно, условия применимости теоремы Тихонова выполнены.

Это означает,

что

присоединенную систему дифференциальных

уравнений можно заменить алгебраическими соотношениями

box

— dy = 0,

ao{l—x

— y) —

x—(box

—

dy)

= 0,

(III.4-10)

полагая

тем

самым концентрации комплексов

ES и ES

постоян-

ными.

Таким образом,

путем

строгого анализа исходной системы

дифференциальных уравнений

мы

убедились

справедливости

до-

пущения

квазистационарном течении процесса

при

условии,

что

имеет место значительное превосходство концентрации

субстрата

над концентрацией фермента

[S]»e

Выразим

из

первого уравнения (II

1.4—10)

переменную

через

и х, а

затем

из

второго

— х

через

ст:

х=

(Ш.4—11)

аа

Р (ао)

где

hi. ^4

k 4

Подставив выражение (II

1.4—11)

вырожденное уравнение

системы

(III.4—9),

получим уравнение ферментативной реакции

с субстратным угнетением

= а

(с+1)ао

=/(

. (Щ.4-12)

аа

{ао)*

' '

215

От известного выражения (III.2—18) последнее уравнение от-

личается свободным членом а, характеризующим скорость поступ-

ления

субстрата в сферу реакции.

Стационарные

точки уравнения (III.4—12) находятся из усло-

вия

= 0, или

(е-г 1) аа

+ аа + {3 (аа)

а.

(Ш.4—13)

Для определения числа и характера особых точек этого урав-

нения

удобно использовать графическое представление зависимо-

сти скорости притока а и расхода субстрата в реакции v от вели-

чины

о. Очевидно, решениям

уравнения (Ш.4—13)

будут

соот-

ветствовать точки пересечения

графика

функции

v(a) =

+ аа

Р {aaf

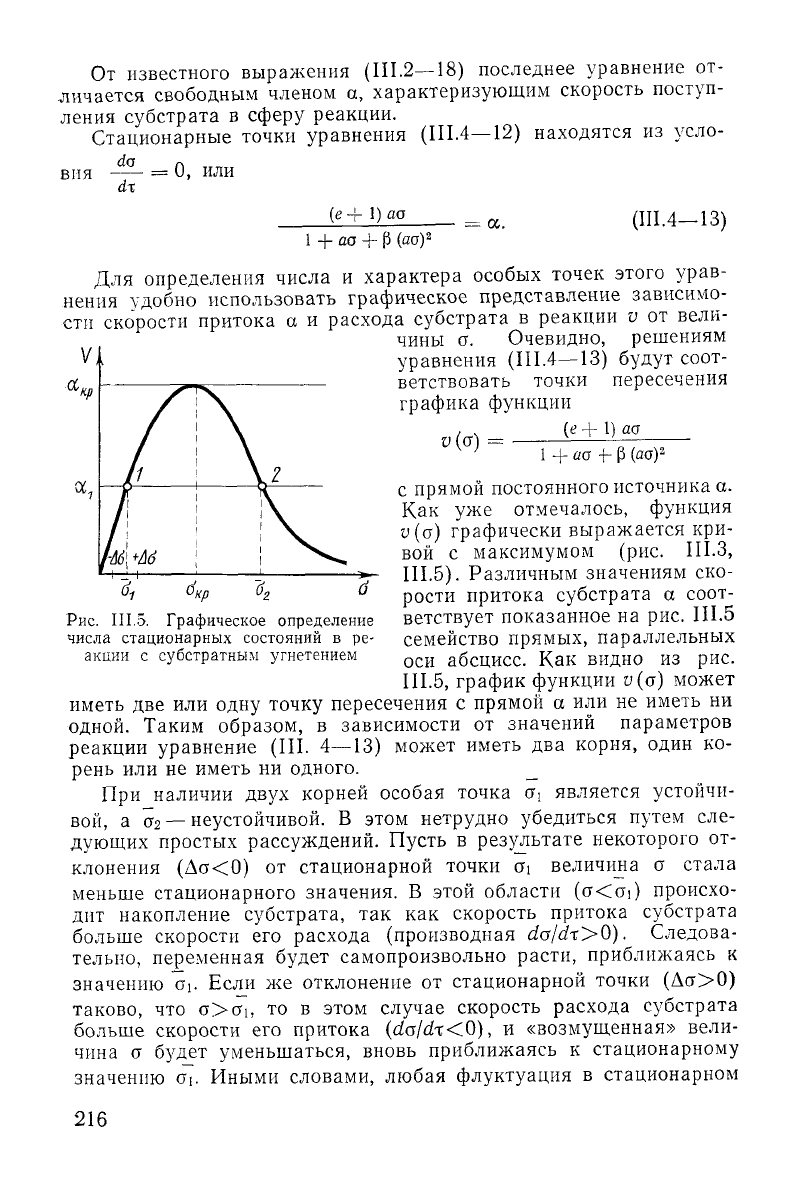
Рис. III.5.

Графическое определение

числа стационарных состояний в ре-

акции

с субстратным угнетением

с прямой постоянного источника а.

Как

уже отмечалось, функция

(а) графически выражается кри-

вой

с максимумом (рис.

III.3,

III.5).

Различным значениям ско-

рости притока субстрата а соот-

ветствует

показанное на рис.

III.5

семейство прямых, параллельных

оси

абсцисс. Как видно из рис.

III.5,

график функции v(a) может

иметь две или одну точку пересечения с прямой а или не иметь ни

одной.

Таким образом, в зависимости от значений параметров

реакции

уравнение (III. 4—13) может иметь два

корня,

один ко-

рень

или не иметь ни одного. _

При

наличии

двух

корней особая точка а

{

является устойчи-

вой,

а аг — неустойчивой. В этом нетрудно убедиться путем сле-

дующих

простых рассуждений. Пусть в

результате

некоторого от-

клонения

(До<0) от стационарной точки о\ величина а стала

меньше стационарного значения. В этой области

(а<о\)

происхо-

дит накопление субстрата, так как скорость притока субстрата

больше скорости его расхода (производная

do/dx>0).

Следова-

тельно, переменная

будет

самопроизвольно расти, приближаясь к

значению а\. Если же отклонение от стационарной точки (Дсг>0)

таково,

что а>а

то в этом

случае

скорость расхода субстрата

больше скорости его притока

(do/dr<0),

и «возмущенная» вели-

чина

будет

уменьшаться, вновь приближаясь к стационарному

значению а\. Иными словами, любая флуктуация в стационарном

216

(<$,<*)>

состоянии

о\

будет

затухать,

и система вернется в исходное поло-

жение:

состояние 0] устойчиво. Аналогичные рассуждения в отно-

шении

стационарной точки о

приводят к выводу о том, что она

носит

неустойчивый характер. Действительно, положительные от-

клонения

(а>0г) выводят систему в область, где скорость притока

субстрата больше скорости его расхода, и, следовательно, вели-

чина

будет

самопроизвольно возрастать, еще дальше

«уводя»

систему от особой точки 02. В

случае

отрицательных флуктуации

(0<0г) скорость притока субстрата становится меньше скорости

оттока

(daldr<0).

В этих условиях величина 0 убывает, отклоне-

ние

системы от исходного положения увеличивается, и система

опять

удаляется от стационарного состояния, которое является,

таким образом, неустойчивым. Этот же вывод легко сделать, опре-

делив знак производной по а правой части f(a, о) выражения

(III.4—12),

который является, соот-

ветственно, отрицательным для 0<

р И ПОЛОЖИТеЛЬНЫМ ДЛЯ 0>0кв

(см.

часть I, гл. 2).

Скорость притока субстрата в сфе-

ру реакции можно рассматривать как

параметр, наиболее удобный для уп-

равления

ферментативной системой; в

уравнении (III.4—12) ему соответст-

вует

безразмерная величина а. По-

смотрим, каким образом изменения

этого параметра

будут

сказываться на

поведении рассматриваемой системы.

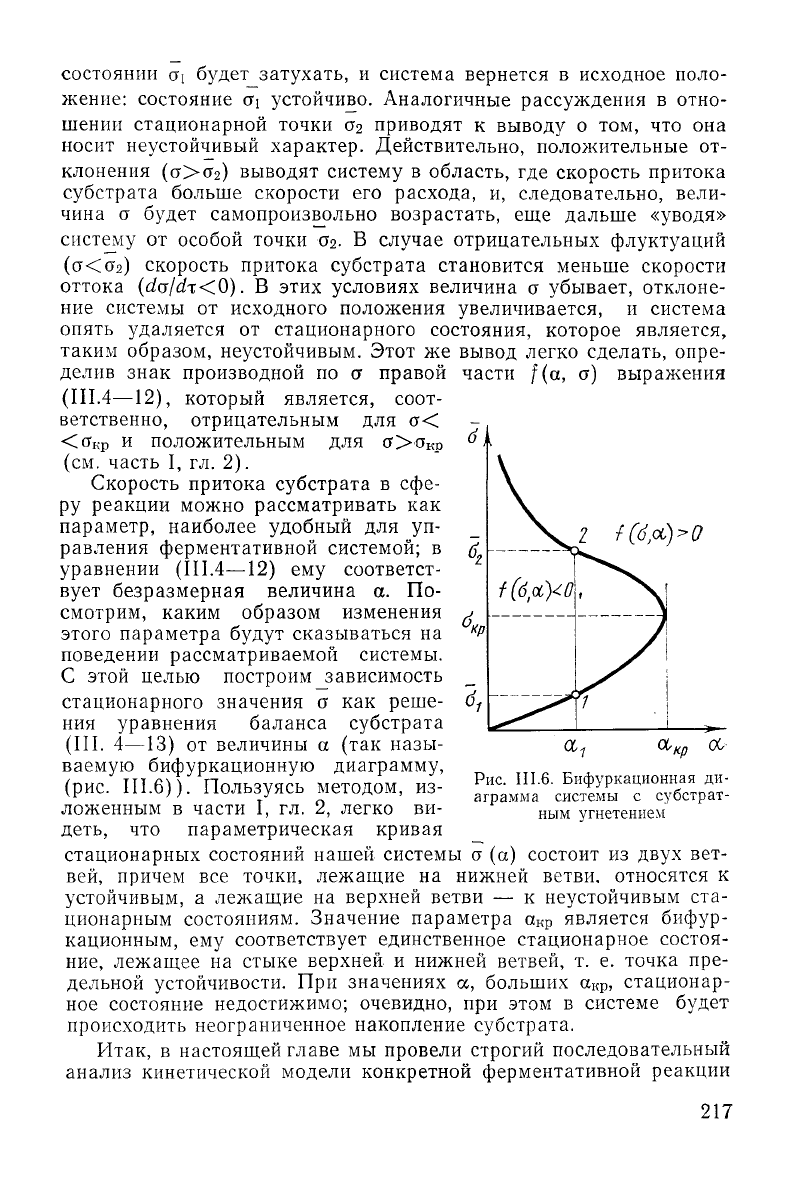
этой целью построим зависимость _

стационарного значения 0 как реше- d

ния

уравнения баланса субстрата

(III.

4—13) от величины а (так назы-

ваемую бифуркационную диаграмму,

(рис.

III.6)).

Пользуясь методом, из-

ложенным в части I, гл. 2, легко ви-

деть, что параметрическая кривая

стационарных состояний нашей системы 0 (а) состоит из

двух

вет-

вей,

причем все точки, лежащие на нижней ветви, относятся к

устойчивым, а лежащие на верхней ветви — к неустойчивым ста-

ционарным

состояниям. Значение параметра а

кр

является бифур-

кационным,

ему соответствует единственное стационарное состоя-

ние,

лежащее на стыке верхней и нижней ветвей, т. е. точка пре-

дельной устойчивости. При значениях а, больших а

р, стационар-

ное

состояние недостижимо; очевидно, при этом в системе

будет

происходить неограниченное накопление субстрата.

Итак,

в настоящей главе мы провели строгий последовательный

анализ

кинетической модели конкретной ферментативной реакции

ОС

Рис.

111.6.

Бифуркационная ди-

аграмма

системы с

субстрат-

ным

угнетением

217

продемонстрировали процедуру ее упрощения методом квази-

стационарных концентраций. При этом мы рассмотрели достаточно

простую реакцию, протекающую с участием одного субстрата и

одного фермента, а также с образованием

двух

промежуточных

комплексов

и одного продукта. Однако и в более сложных слу-

чаях, следуя описанной процедуре «обезразмеривания» и выделе-

ния

малого параметра, можно свести математическое описание

ферментативного процесса к одному-двум уравнениям. В следую-

щих

главах,

посвященных рассмотрению важных нелинейных

свойств ферментативных систем, мы не

будем

воспроизводить тех-

нологию упрощения исходной системы дифференциальных уравне-

ний,

надеясь, что читатель достаточно с ней знаком.

Глава

МНОЖЕСТВЕННЫЕ СТАЦИОНАРНЫЕ

СОСТОЯНИЯ.

ТРИГГЕРНЫЕ СВОЙСТВА

ФЕРМЕНТАТИВНЫХ СИСТЕМ

Рассмотрим еще один, несколько усложненный по сравнению с

предыдущим пример открытой ферментативной системы — реак-

цию

с субстратным угнетением и обратимой реакцией притока

субстрата (Сельков,

19676)

*+1

-f2

^ p\.. (Ш.5—1)

От предыдущего примера схема (Ш.5—1) отличается лишь функ-

цией

источника: в данном

случае

скорость притока субстрата ли-

нейно

убывает

с увеличением концентрации [S]

= о

—

k-\[S\,

где Vi — общая скорость изменения субстрата.

Аналогичным образом описывается источник при наличии побоч-

ного стока субстрата

218

Соответствующая

схеме

(III.5—1) система дифференциальных

уравнений такова:

-^f

= *+i [So] - *-i [5] - k

[S] [Е] -

k+, [SE] [S] + £_

[S*E],

(III.5-2)

[S] [£J - (£_

+ Л,) [SE] -

d[S

]

= k

[S][SE] -£_

[&E],

- k

[S] [E]

где,

как и в

предыдущем примере,

[Е]

+ [SE] + [S

£] =

const

= е

, e

С К

Опуская расчеты, связанные

выделением малого параметра,

выпишем уравнения

для

медленных .переменных системы (Ш.5—2)

о - " 11 ч

1 + а +

•

dt I + а

+Y<T

Здесь введены следующие безразмерные величины:

—

бр. (Ш.5—3)

Р—

= —• , Т —-

Первое

из

уравнений (Ш.5—3)

не

зависит

от р и

может быть

исследовано отдельно. Воспользуемся,

как и

прежде, графическим

представлением

найдем стационарные решения этого уравнения

— р

°—

(Ш.5—4)

как

точки пересечения графика функции

v(a)

расхода субстрата

реакции

прямой источника Vi=a—pa

(рис.

III.7).

Как

видно

из

219

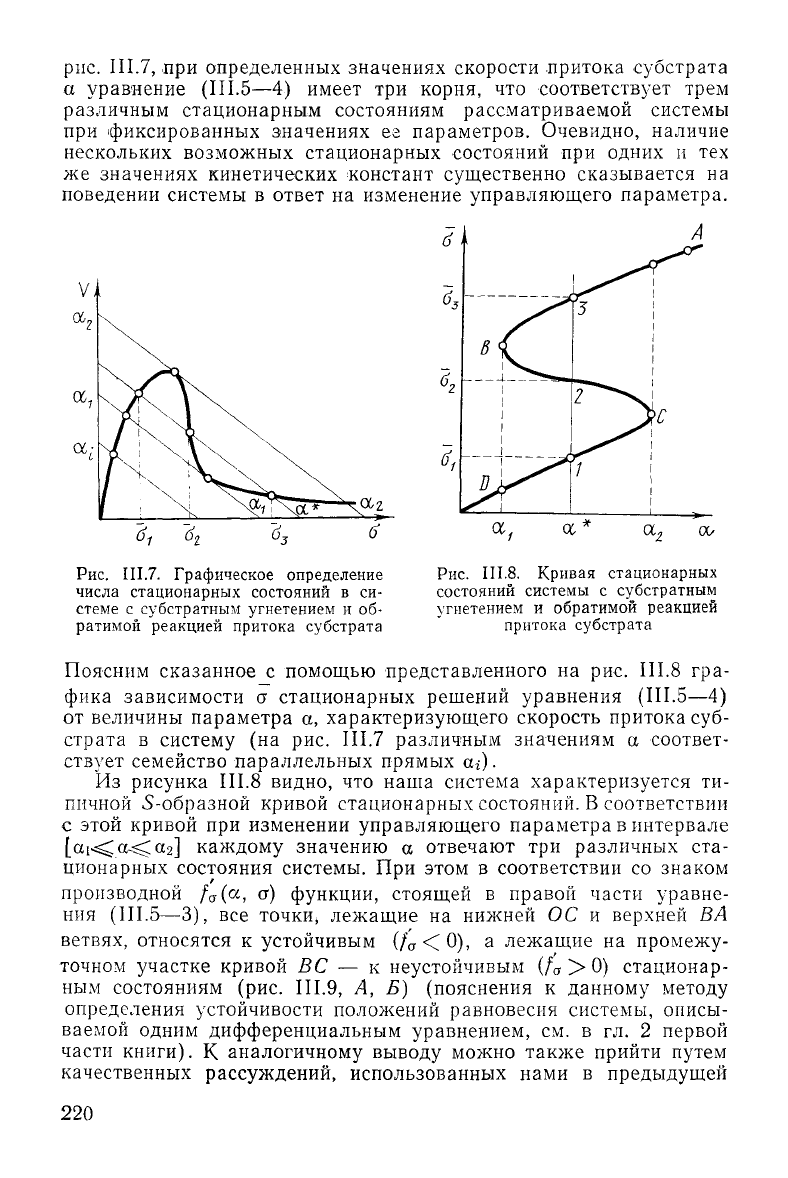
рис.

III.7,

при определенных значениях скорости притока субстрата

а уравнение (III.5—4) имеет три корня, что соответствует трем

различным стационарным состояниям рассматриваемой системы

при

фиксированных значениях ег параметров. Очевидно, наличие

нескольких возможных стационарных состояний при одних и тех

же значениях кинетических констант существенно сказывается на

поведении системы в ответ на изменение управляющего параметра.

Рис.

III.7.

Графическое определение

числа стационарных состояний в си-

стеме с субстратным угнетением и об-

ратимой

реакцией притока субстрата

Рис.

III.8.

Кривая стационарных

состояний

системы с субстратным

угнетением и обратимой реакцией

притока

субстрата

Поясним

сказанное с помощью представленного на рис.

III.8

гра-

фика

зависимости а стационарных решений уравнения (III.5—4)

от величины параметра а, характеризующего скорость притока суб-

страта в систему (на рис.

III.7

различным значениям а соответ-

ствует

семейство параллельных прямых а*).

Из

рисунка

III.8

видно, что наша система характеризуется ти-

пичной

S-образной кривой стационарных состояний. В соответствии

с этой кривой при изменении управляющего параметра в интервале

[а^а-^ссг] каждому значению а отвечают три различных ста-

ционарных

состояния системы. При этом в соответствии со знаком

производной

/cj(a, а) функции, стоящей в правой части уравне-

ния

(III.5—3), все точки, лежащие на нижней ОС и верхней ВА

ветвях, относятся к устойчивым (/

ст

<0), а лежащие на промежу-

точном участке кривой ВС — к неустойчивым (Д, > 0) стационар-

ным

состояниям (рис.

III.9,

А, Б) (пояснения к данному

методу

определения устойчивости положений равновесия системы, описы-

ваемой одним дифференциальным уравнением, см. в гл. 2 первой

части книги). К аналогичному выводу можно также прийти путем

качественных рассуждений, использованных нами в предыдущей

220