Рубин А.Б., Пытьева Н.Ф., Ризниченко Г.Ю. Кинетика биологических процессов

Подождите немного. Документ загружается.

Соответствующее ей характеристическое уравнение

— Я р

—

р.

8,Х,

(II.5-17)

Вычислив коэффициенты характеристического уравнения, получим

для определителей Гурвица, что

Ai>0

Аг>0,

ДЗ =

Д2ЙЗ,

откуда

необходимым и достаточным условием устойчивости системы яв-

ляется выполнение неравенства

(П.5—18)

что при подстановке х

8-2

равносильно второму из соотноше-

720

16 32 48 64 80 96 t

ний

(II.5—14). Следовательно, выполнение соотношения (П.5—14)

является достаточным условием существования положительной,

асимптотически устойчивой стацио-

нарной

точки. Выполненное на анало-

говой машине изучение поведения этой

системы для разных значений

коэффи-

циентов

показало, что решения име-

ют вид

затухающих

колебаний

(рис.

П.5). Если же реализуются не-

равенства (П.5—15), условия Гурвица

не

выполняются и стационарная точка

неустойчива.

Итак,

проведенное исследование

показало,

что системы с неразветв-

ленными

связями

между

трофически-

ми

уровнями без

учета

ограниченно-

сти костной компоненты (П.5—1) об-

ладают

следующими свойствами:

а) если число видов п нечетное, то соответствующая система

уравнений (П.5—1) несовместна и не может описывать реальный

биоценоз;

б) если число видов п — четное, система (П.5—1) нахо-

дится на границе устойчивости, и любая случайная флуктуация

может привести к ее вырождению, что, по-видимому, также не со-

ответствует

положению дел в реальном биоценозе.

Учитывая ограниченность абиотической компоненты, мы прихо-

дим к системе уравнений (И.5—2), имеющей единственное устой-

чивое стационарное состояние, причем поведение компонентов си-

стемы при разных значениях коэффициентов может быть различ-

ным,

в частности, иметь вид

затухающих

колебаний.

Отметим, что влияние природных ресурсов неорганического

происхождения на развитие биоценозов может иметь различный

Рис.

П.5. Поведение перемен-

ных систем (П.5—2а) во

времени (Эман, 1966)

141

характер, что, естественно,

требует

различного математического

описания.

Например, для растительности ограничивающим факто-

ром

будет

не количество питательных веществ в почве, а ограни-

ченный

поток солнечной энергии.

В общем

случае

это поток любо-

го вещества, необходимого для

существования первого вида.

Пусть величина такого потока

p = const. Таким образом, с уве-

личением биомассы первого вида

на

единицу биомассы

будет

при-

ходиться все меньшее количество

энергии.

Если

остальные виды развивают-

ся

по тем же законам, что и в

рассмотренных ранее моделях

системы уравнений (П.5—1),

(П.5—2),

а для малого At увеличние биомассы первого вида за

счет размножения происходит по закону

Аи = е*р (1 — er"i), е> = е!,

где е* и / — постоянные положительные числа, то система уравне-

ний

модели

будет

иметь вид

;

е) s

(Н.5—19)

—~ = Mi-i — Si —

Sf+iXi+i)

i = 2, 3 n 6

л+1

= 0.

Как

показало исследование, стационарная точка биогеоценоза,

развитие первого вида которого зависит от притока р, всегда

асимптотически устойчива, незатухающих циклов кинетики популя-

ций

в такой системе быть не может. Решение представляет собой

либо затухающие колебания около стационарной точки, либо

асимптотически стремится к стационарной точке.

Итак,

совместное рассмотрение живых и костных компонентов

ценоза,

на необходимость которого в биологическом исследовании

неоднократно

указывал Н. В. Сукачев (1947), оказывается необ-

ходимым и при математическом моделировании экосистем. Изоли-

рованное

рассмотрение лишь биологических компонентов ценоза

приводит к неудовлетворительным результатам: отсутствию ста-

ционарных

решений при нечетном числе видов и негрубости систе-

мы при четном числе видов в модели (II.5—1).

142

Глава

МАТЕМАТИЧЕСКИЕ

МОДЕЛИ

ЗАМКНУТЫХ

ПО

МАССЕ

ЭКОЛОГИЧЕСКИХ

СИСТЕМ

Большой

интерес для понимания процессов, происходящих в

естественных ценозах, представляет изучение искусственных эко-

логических систем, особенно в связи с освоением человеком кос-

мического пространства. Пребывание человека в условиях длитель-

ного космического полета

требует

снабжения его всем необходи-

мым для жизни, в первую очередь кислородом и пищей, а также

рядом

других

факторов, которые в совокупности

могут

быть обес-

печены лишь в условиях длительно существующей экосистемы на

борту космического корабля. Ясно, какое значение имеет построе-

ние

правильной математической модели в создании длительного

круговорота вещества и энергии в ограниченных по объему и числу

звеньев экологических системах. В искусственных экосистемах есть

возможность стабилизировать условия, внешние по отношению к

изучаемой системе, обеспечить замкнутость системы по массе опре-

деленных веществ, детально следить за процессами энерго- и мас-

сообмена

между

компонентами.

Построению

и исследованию математических моделей замкну-

тых экосистем посвящено значительное количество работ, на ре-

зультатах

которых мы кратко остановимся. Прежде всего отметим

два важных обстоятельства, обусловливающих особенности пред-

ложенных моделей.

Существенной особенностью уравнений Вольтерра является пх

нелинейный

характер, обусловленный механизмом свободного би-

нарного

взаимодействия популяций по типу сталкивающихся час-

тиц.

Очевидно, что в искусственных системах вероятностный харак-

тер взаимодействия видов (хищник — жертва) имеет место, лишь

когда последние содержатся в одном объеме, который значительно

превосходит общий объем организмов. Однако

существуют

и дру-

гие случаи, когда сохраняется нелинейный характер уравнений

переноса. Действительно, рассмотрим некий произвольный участок

цепи

переноса вещества

Пусть Xi_

i+x

— концентрации биомассы в (t—1), i, (t+1)

звеньях системы. Отток биомассы от (г—1)-го звена описывается

линейным

уравнением вида

*i-i = — h~\,i Xi-i. (II. 6—2)

В искусственной системе регуляция оттока биомассы от донора

*г_1 должна осуществляться оптимальным образом, в соответствии

143

с потребностями акцептора x

. Это можно осуществить, задав, на-

пример,

зависимость константы ki-\

переноса от концентрации

акцептора Х

В виде

*;_,,, = Ai_

. (II.6-3)

учетом

(И.6—3) уравнение (II.6—2) примет нелинейную форму

вольтерровского типа

x\-i = —

ki~\,i

XiXi-u

(II.6—4)

Таким

образом, введение в модели искусственных экосистем

нелинейных

членов существенно обогащает их математические

свойства и

делает

их сходными с моделями естественных биоцено-

зов.

Другим важным обстоятельством является сохранение общей

массы в закрытой системе, что вызывает необходимость наложе-

ния

соответствующих условий на переменные в системе уравнений.

В работах А. Б. Рубина и А. С. Фохта

(1968)

были рассмот-

рены

уравнения обменных процессов в замкнутых по массе систе-.

мах, имеющих общий вид

- £

ksjXsXj,

S = 1, 2 п, (П.6—5)

где k

j — константа взаимодействия звеньев x

и х,, п — общее

число звеньев системы, причем k

j =

—kjs.

Отсюда

следует,

что

Е Е

XsX

= °

(П.6-6)

и, следовательно,

: const. (И.6—7)

s=\

Выражение (II.6—7) соответствует закону сохранения массы в

закрытой системе.

Исследование на устойчивость показало, что система (II.6—5)

аналогична по своим свойствам модели (II.5—1).

При

п четном ее определитель не равен нулю и она обладает

особой точкой типа центр, т. е. находится на границе устойчиво-

сти.

При п нечетном определитель равен нулю и система уравне-

ний

несовместна.

Существующие в настоящее время искусственные системы на

самом

деле

не являются полностью замкнутыми, поскольку для

поддержания в них круговорота вещества требуется дополнитель-

ное

введение из внешней среды тех или иных компонентов. В этом

отношении

искусственные комплексы приближаются к природным

144

биоценозам, когда в них рассматривается участок цепи трофиче-

ского переноса, возможность выделения которого из общей систе-

мы зависит от биологических особенностей сообщества. Допустим

в связи с этим, что в модели (II.6—5) каждый из компонентов

может обмениваться с внешней средой по реакциям первого по-

рядка

= V

ks.xsxj

(II.6—8)

/'-—1

В такой модели условие сохранения массы уже не выполняется

(IJSSXS¥=0),

оказывается, что при п четном особая точка принад-

лежит типу центр, а при п нечетном уравнения несовместны.

Инте-

ресно отметить, что в последнем

случае

можно искусственно нало-

жить условия связи

между

коэффициентами, которые

делают

си-

стему

уравнений совместной. В этом

случае

мы получим вырож-

денную систему,

обладающую

целой совокупностью особых точек

типа центр, а условия связи совпадают с условиями сохранения

общей массы системы.

Например,

такими свойствами

обладает

модель

е, ki le

—^

У\-^

—^ S\v

—>•

J\Q —>*

Рассмотренные модели представляют собой вырожденные не-

грубые

системы, обладающие совокупностью состояний безразлич-

ного равновесия, причем движение от одной особой точки к

другой

•совершается под влиянием малых возмущений. Вблизи этой сово-

купности особых точек в фазовом пространстве образуются зам-

кнутые траектории, соответствующие установлению колебатель-

ного режима.

Очевидно, что в целом такие системы представляют собой раз-

новидность модели Вольтерра и также не являются устойчивыми

в указанном выше смысле. Тем не менее дальнейшее развитие та-

кого рода моделей, которые мы сейчас рассмотрим, позволило

обнаружить у них целый ряд интересных свойств, и в том числе,

в отличие от системы Вольтерра, устойчивые стационарные состоя-

ния

при условии сохранения полной массы системы, включая и

массу биогенных элементов, содержащихся в костной компоненте

•системы (резервуар питательных веществ, почвы, раствор солей в

воде

и пр.).

До сих пор мы исследовали модель экологической системы,

каждый компонент которой представляет собой нерасчлененный

145

на

виды трофический уровень. Подобный

подход

при моделирова-

нии

природных систем не позволяет проследить за динамикой чис-

ленности

каждого вида в отдельности и выяснить, как

структура

(видовой состав) каждого трофического уровня влияет на устой-

чивость экосистемы в целом. Решения систем уравнений для от-

дельных видов и для трофических уровней, вообще говоря, не сов-

падают

друг

с другом, и применять вольтерровские уравнения типа

(II.5—2)

для описания общей численности (биомассы) особей на

том или ином трофическом уровне можно только в том случае,

если трофические уровни включают близкие виды.

В связи с этим в работах В. В. Алексеева

(1973)

изучались

случаи, когда на каждом уровне находится несколько конкурирую-

щих видов, и трофические взаимодействия

между

видами — про-

дуцентами (жертвы) и консументами (хищники) разных порядков

носят

различный характер.

Например,

хищники могли питаться с одинаковой вероятностью

всеми видами жертв или преимущественно одним или несколькими

видами—жертвами. Переменными, входящими в уравнения моде-

лей В. В. Алексеева, являются не сами биомассы видов, а общие

массы того или иного вещества, содержащегося в организмах

каждого вида.

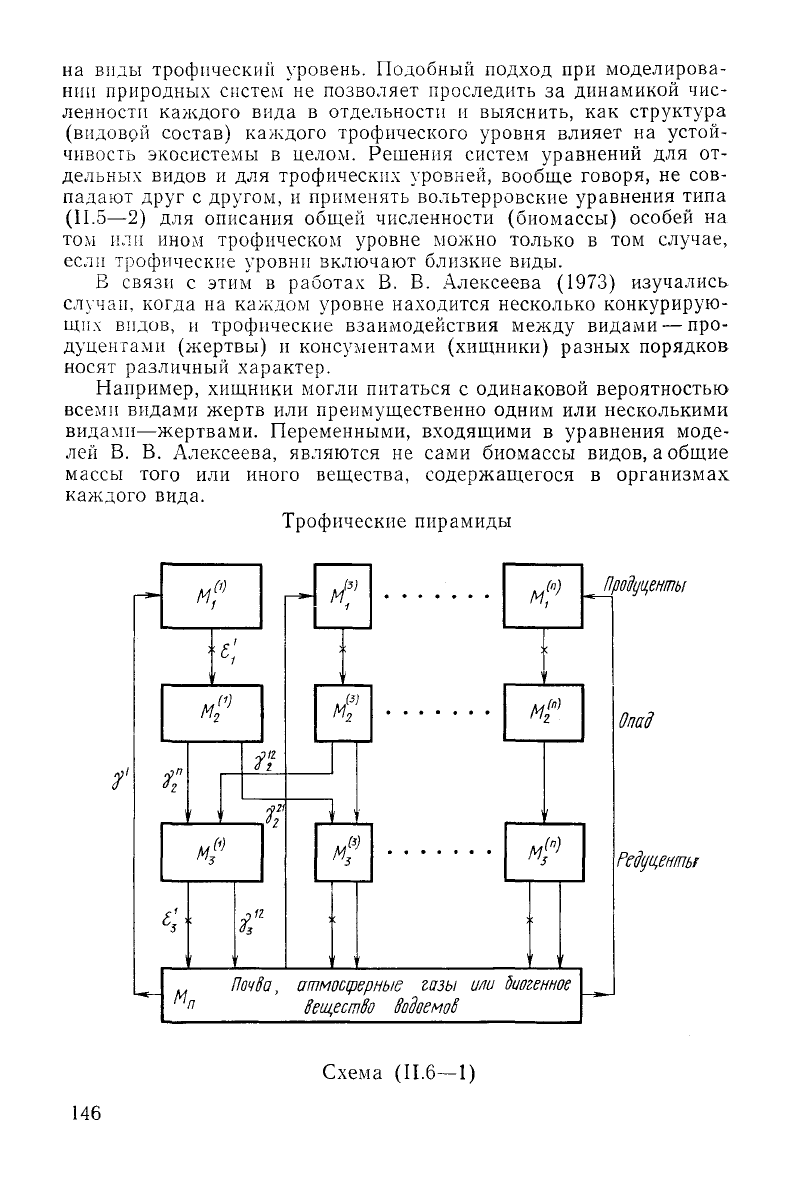
Трофические

пирамиды

Г*"

ПочВа,

«Г

м»

атмосферные газы или

Ъиогенное

Вещество

Моемое

Jl-

Опад

Редуцент

146

Схема (II.6—1)

Рассмотрим циркуляции вещества в системе, состоящей из рас-

тений (продуцентов)

(М\

опада (М^), редуцентов

(Мз*),

минера-

лизующих опад, и почвы (Л1

) (схема стр. 146). Перечеркнутыми

стрелками обозначены потоки вещества, определяемые процессом

отмирания живых организмов. Скорости этих процессов считаются

пропорциональными биомассе соответствующих видов (линейные

члены в уравнениях). Простыми стрелками обозначены потоки ве-

щества, обусловленные активными взаимодействиями живых орга-

низмов

друг

другом

и с неживой природой. Скорости таких про-

цессов предполагались, следуя Вольтерра, пропорциональными

вероятности встречи особей разных видов

друг

с другом, т. е. про-

изведению масс вещества, заключенного в каждом из взаимодей-

ствующих блоков системы (билинейные члены в уравнениях).

Резервуар минеральных питательных веществ М

является об-

щим для п трофических пирамид, причем

между

видами на разных

трофических уровнях

могут

осуществляться всевозможные взаимо-

действия. Чтобы не загромождать

схему,

на ней указаны лишь

некоторые из потоков вещества

между

компонентами системы.

Итак,

система включает почву М

~ и обладает тремя уровнями

(продуценты M

(

, опад Mf и редуценты Mf), на каждом из которых

имеется п компонентов (i = 1, 2, ... , п).

Система уравнений, описывающая потоки вещества, приведен-

ные на

схеме

II.6—1,

имеет вид

<а

- 8

° Mf ~ SYPM^M

, (И.6-9)

k=l

Здесь верхние индексы указывают номер трофической пирами-

ды, а нижние — номер трофического уровня, которому принадле-

жит соответствующий вид.

Все е и у — постоянные положительные числа, е'/' и ез*-—ко-

эффициенты

естественной смертности продуцентов и редуцентов

i-той пирамиды, Yi

l) и

Уз'*' — коэффициенты роста продуцентов и

редуцентов i-той пирамиды. Так как прирост биомассы редуцентов

происходит только за счет опада от

всех

п пирамид, константа

•скорости роста редуцентов Уз'' не должна превышать константу

(ik)

поступления опада Y2 , т. е. должны выполняться соотношения

> Y3 •

147

системе (II.6—1) сохраняется общая масса компонентов.

Дей-

ствительно, сложив уравнения

(II.6—9),

получим

3 п

_iL (

„ у

УмуА

= о, (П.б-ю>

т. е.

3 п

Мп

~ Е X ^

= const-

Обозначив через

Л!

массу всего биогеоценоза, будем иметь

Выберем два произвольных уравнения из II.6—9, пусть это

будет

р-тое и

£-тое

уравнения. Умножим первое из них на y

а второе на y^lM®. Вычтем затем из первого уравнения второе

интегрируя, получим

с ex

t] = A,

где с = const. Пусть теперь

В этом

случае

Л->0. Но величина М^ ограничена

сверху

значе-

нием

М. Поэтому M

(

->0, т. е. р-тый вид вытесняется Л-тым ви-

дом, у которого отношение

e'f'/Y^'

меньше. Условие равновесия

видов, т. е. совместного бесконечно долгого существования на од-

ном

и том же трофическом уровне, имеет вид

р)

Оно

очень жесткое и в природе вряд ли может быть выполнено.

Повторяя

аналогичную процедуру для

всех

пар уравнений (П.6—9),

получим, что в

результате

конкурентной борьбы

между

продуцен-

тами в отсутствие консументов выживает вид 5 с наименьшим

значением отношения коэффициента смертности ef к коэффициен-

ту роста Yi независимо от характера связей редуцентов с опадом-

148

В фазовом пространстве, по осям которого отложены биомассы

видов, траектории системы

будут

сходиться к одной устойчивой

особой точке, соответствующей состоянию, в котором элиминиру-

ются виды

всех

трофических пирамид, кроме одной, где отношение

(

/Yi

' наименьшее. Устойчивость подобной одной трофической

пирамиды с

учетом

костной компоненты системы М

была пока-

зана в предыдущей главе.

Отношение

ef\/y\

определяется, с одной стороны, свойствами

организмов, а с

другой

— внешними условиями: температурой,

влажностью и химическим составом среды. Это позволяет сделать

вывод, что, подбирая условия жизни биоценоза так, чтобы отно-

шение

e'^'/Yi

было минимальным для интересующего нас вида,

мы тем самым создаем условия для устранения нежелательных

конкурентов.

Перейдем теперь к рассмотрению роли консументов в сообще-

стве. Рассмотрим случай, когда травоядные животные узкоспециа-

лизированы. Соответствующая схема трофических связей изобра-

жена на

схеме

II.6—2 (см. стр. 150). Здесь, как и раньше, нане-

сены только отдельные связи

между

редуцентами и опадом. Сис-

тема уравнений, описывающая данный биогеоценоз, имеет вид:

— e

(

i° M

(

i° — Yi° M

Mf -г У

и)

{

Р М

(И.6—11)

}

_ „(<>

U) , JO л/КО i. (J.n J»\ Л/Г« м(0 V y№

Система со специализированными консументами (уравнения

(И.6—11)) в отличие от системы без консументов (уравнения

(II.6—9)) не вырождается в одну трофическую пирамиду; суще-

ствуют

устойчивые стационарные состояния, ненулевые для не-

скольких видов продуцентов и соответствующих им специализиро-

ванных консументов. Это объясняется тем, что введение специали-

зированных консументов приводит к ослаблению конкурентного

воздействия продуцентов

друг

на

друга,

так как соответствующий

консумент ограничивает увеличение численности наиболее приспо-

собленного продуцента и препятствует вытеснению остальных ви-

дов растений. Буферная система, состоящая из опада и редуцен-

149

•

;

'п

почба,

;

ел

—1

«Г

пирамид

-Г

а тмосферные

вещества

газы

или

биогенные •

Водоёмов

консументы

продуценты

опад

редуценты

Схема (И.6—2)

тов, определяет количество минерализуемого вещества

поэто-

му— биомассу

количество

пар

продуцент

—

консумент,

но не

сказывается

на

взаимодействии

между

теми парами,

для

которых

данной системе

существует

стационарное состояние.

Таким

образом, система

со

специализированными консументами

более стабильна,

чем без

консументов, которая вырождается

в ко-

нечном

итоге

одновидовую систему

оказывается поэтому очень

чувствительной

резким изменениям внешних условий, происхо-

дящим

вслед

за

периодом продолжительного

их

постоянства.

Од-

нако,

если консументы неспециализированы, например если один

консумент поедает

все

продуценты системы,

это

приводит,

как и

случае

отсутствия консументов (П.6—2),

течением времени

одной

простой пищевой цепи, которая неустойчива

по

отношению

резким изменениям внешних условий.

природе чаще всего наблюдается некоторый промежуточный

случай, когда консументы преимущественно питаются одним

или

150