Рубин А.Б., Пытьева Н.Ф., Ризниченко Г.Ю. Кинетика биологических процессов

Подождите немного. Документ загружается.

периодическую зависимость от времени с более коротким перио-

дом. По результатам моделирования эти явления можно объяс-

нить

тем, что внутренний период неизменен и меньше внешнего,

но

проявляется при непрерывном освещении.

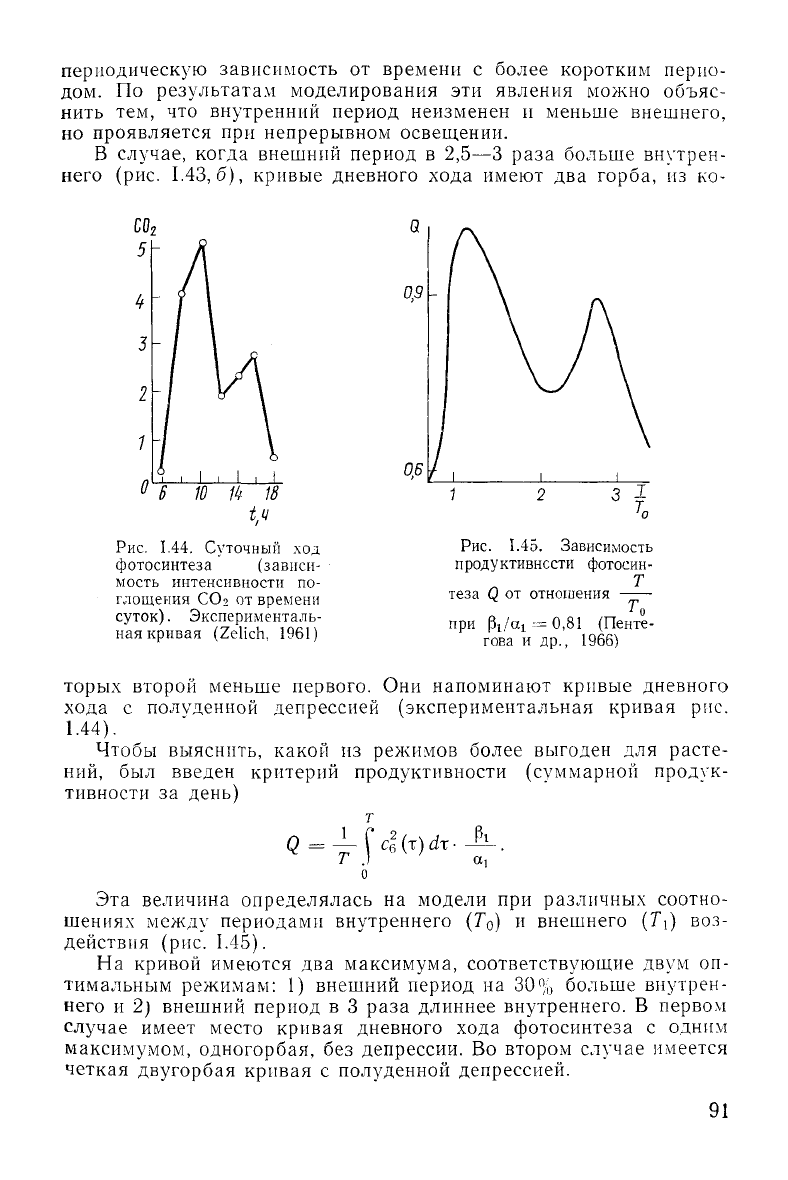
В случае, когда внешний период в

2,5—3

раза больше внутрен-

него (рис.

1.43,6),

кривые дневного

хода

имеют два горба, из ко-

0,9

0.6

Рис.

1.44. Суточный ход

фотосинтеза (зависи-

мость интенсивности по-

глощения СОз от времени

суток). Эксперименталь-

ная

кривая (Zelich, 1961)

Рис.

1.45. Зависимость

продуктивности фотосин-

теза и от отношения

при

рх/tt! = 0,81 (Пенте-

гова и др., 1966)

торых второй меньше первого. Они напоминают кривые дневного

хода

с полуденной репрессией (экспериментальная кривая рис.

1.44).

Чтобы выяснить, какой из режимов более выгоден для расте-

ний,

был введен критерий продуктивности (суммарной продук-

тивности за день)

Эта величина определялась на модели при различных соотно-

шениях

между

периодами внутреннего (Т

) и внешнего (Т

{

) воз-

действия (рис.

1.45).

На

кривой имеются два максимума, соответствующие

двум

оп-

тимальным режимам: 1) внешний период на 30% больше внутрен-

него и 2) внешний период в 3 раза длиннее внутреннего. В первом

случае

имеет место кривая дневного

хода

фотосинтеза с одним

максимумом, одногорбая, без депрессии. Во втором

случае

имеется

четкая двугорбая кривая с полуденной депрессией.

На

этом основании можно

думать,

что полуденная депрессия

фотосинтеза есть способ адаптации организма к внешним усло-

виям.

Дело в том, что в

случае

режима с полуденной депрессией

растение быстрее

входит

в режим интенсивного фотосинтеза и пол-

нее использует утренние и вечерние часы дня. Полуденная депрес-

сия

с этой точки зрения просто

«плата»

за быстрый

вход

в режим,

так

как быстрота

входа

зависит от периода эндогенного ритма.

При

отсутствии депрессии растение вынуждено входить в режим

медленно и, хотя

«работает»

днем,

«теряет

время» утром и вече-

ром.

Два максимума на кривой рис. 1.45 соответствуют тому факту,

что среди различных видов растений

существуют

такие, для кото-

рых естественным является режим вблизи первого максимума —

величина Q (кривая дневного

хода

при этом не имеет максимума).

Растения,

для которых характерно понижение продуктивности фо-

тосинтеза в середине дня, характеризуются полуденной депрессией.

Выгодность того или иного режима определяется географической

широтой и условиями климата, причем зеленые клетки

могут

при-

способиться к внешним условиям, изменяя величину своего внут-

реннего эндогенного ритма.

Глава

ПРОБЛЕМЫ

БЫСТРЫХ И

МЕДЛЕННЫХ

ПЕРЕМЕННЫХ.

ТЕОРЕМА

ТИХОНОВА

Одной из основных проблем математического моделирования

является проблема выбора существенных переменных, необходи-

мых и достаточных для построения адекватной математической мо-

дели изучаемого объекта. Полная модель, учитывающая все де-

тали процессов, протекающих в данном объекте, может быть на-

столько сложной, что качественное исследование ее в общем виде

невозможно.

Для анализа такой модели необходимо задавать кон-

кретные численные значения ее парахметров. Машинный счет с

помощью ЭВМ позволяет получить точное решение в каждом кон-

кретном

случае

(при определенных наборах коэффициентов), но

не

дает

представления о поведении системы в достаточно широкой

области изменения параметров.

Как

уже говорилось, задача исследователя состоит в том, чтобы

построить модель явления, содержащую возможно меньшее число

переменных и произвольных параметров и в то же время правиль-

но

отражающую основные свойства этого явления (например

устойчивость, колебательность, триггерные свойства и т. д.). Если

увеличение числа переменных не меняет существенно общих

свойств модели, такие дополнительные переменные являются

«лишними»,

и их не

следует

включать

модель. Сейчас

мы зай-

мемся рассмотрением вопроса

том,

каких

случаях,

не

утрачи-

вая основных свойств моделируемого объекта, можно сократить

исходное число переменных

и тем

самым упростить модель.

Эта проблема оказывается относительно легко разрешимой

случае,

когда

системе имеет место

так

называемая иерархия

времен; совместно протекающие процессы сильно отличаются

по

своим характерным временам.

Для

группы быстро изменяющихся

переменных можно

не

записывать дифференциальных уравнений,

поскольку они практически мгновенно

по

сравнению

остальными

более медленными

достигают

своих стационарных значений.

Тогда

для быстрых переменных вместо дифференциальных уравнений,

описывающих

их

поведение

во

времени, можно записать алгебраи-

ческие уравнения, определяющие

их

стационарные значения.

Эти

значения

быстрых переменных

могут

быть представлены

диффе-

ренциальные уравнения

для

медленных переменных

качестве

параметров. Таким образом, осуществляется редукция,

т. е.

уменьшение числа дифференциальных уравнений полной системы,

которая теперь

будет

включать лишь медленные переменные, зави-

сящие

от

времени.

В химической кинетике такой

метод

был

предложен впервые

Боденштейном

(1913)

получил название

метода

квазистационар-

ных концентраций. Обычно

он

применяется

при

исследовании

си-

стем химических реакций, промежуточные продукты которых

яв-

ляются частицами

высокой реакционной способностью.

таким

реакциям относятся

первую

очередь

все

каталитические процес-

сы,

также свободнорадикальные

цепные реакции.

Важной особенностью процессов,

идущих

участием

активных

промежуточных частиц, является установление

за

малый проме-

жуток времени

(за

который относительное изменение концентра-

ций

исходных веществ невелико) режима,

при

котором разность

скоростей образования

расходования

промежуточных

со-

единений становится малой

по

сравнению

этими скоростями.

Это означает,

что

концентрация промежуточных веществ практи-

чески

не

меняется. Такой режим называется квазистационарным,

а отвечающие

ему

концентрации активных промежуточных

час-

тиц

—

квазистационарными концентрациями.

В квазистационарном режиме дифференциальные уравнения

для изменений концентраций каждого

из

промежуточных соедине-

ний

JEL

rW-t$(i=\,2 0

можно заменить, пренеорегая малой величиной

алгебраиче-

скими

1#>

оЮ (1

1,2,...,/).

Здесь

i>(p и

являются функциями концентраций исходных

ве-

ществ

самих активных промежуточных соединений, поэтому

из

/ алгебраических уравнений можно выразить

квазистационарных

концентраций

активных промежуточных частиц через концентра-

ции

стабильных химических веществ.

По

мере расходования этих

веществ квазистационарные концентрации промежуточных соеди-

нений

будут

изменяться,

но

если время установления квазистацио-

нарного режима мало,

он не

будет

нарушаться

на

протяжении

всего процесса.

Конечно,

такое рассмотрение неправомерно

на

начальных

ста-

диях процесса,

течение которых концентрации промежуточных

частиц изменяются

от

нуля

до

своих квазистационарных значений.

Этот период носит название периода индукции. Разработке

метода

квазистационарных концентраций

(КХЖ) и

оценке длительности

периода индукции посвящены работы Бенсона (1964), Семенова,

Франк-Каменецкого

(1967)

и др.

Метод квазистационарных концентраций получил строгое мате-

матическое обоснование

работах

А. Н.

Тихонова.

Он

(1952)

до-

казал

теорему,

устанавливающую условия,

при

которых возможна

редукция системы уравнений, переменные которой изменяются

различными характерными временами. Дальнейшей математиче-

ской

разработке этих вопросов посвящены работы Васильевой

(1973), Понтрягина (1957), Вазова (1968).

Особенно плодотворен такой

подход

при

изучении

моделиро-

вании

биологических систем,

которых одновременно протекают

быстрые процессы ферментативного катализа

(т~

lO^-f-10~

с),

физиологические процессы (порядка минут)

процессы репродук-

ции

(от

нескольких минут

больше).

Итак,

рассмотрим некоторый процесс, описываемый системой

двух

дифференциальных уравнений:

, .

(1.9-1)

G(x,y),

где

является медленной,

ах —

быстрой переменной.

Это

озна-

чает,

что

отношение приращений

Дг/ и Дх за

короткий промежу-

ток

времени

Д^

много меньше единицы: ——

Ах

Запишем

систему

(1.9—1)

более удобном

для

исследования

виде: воспользуемся

тем

фактом,

что

скорость изменения

значи-

тельно превосходит скорость изменения

у. Это

позволяет предста-

вить функцию

ф(х, у) в

виде произведения некой большой вели-

чины

Л^>1

на

функцию

F(x, у),

соответствующую

по

порядку

величины функции

G(x, у).

Итак,

мы преобразовали второе уравнение системы

(1.9—1)

к виду

AF(x,y).

Разделив

левую

и правую части этого уравнения на А и обо-

значив

е= —, получим полную систему уравнений, тождествен-

/л.

ную системе (1.9—1):

^=-F(x, у),

(1.9-2)

где e<Cl. Упростить полную систему

(1.9—2)

можно, только если характер

решения

этой системы не изменится

при

устремлении малого параметра е

нулю. В таком

случае

мы можем

совершить этот предельный переход и

получить из второго дифференциаль-

ного уравнения системы

(1.9—2)

алге-

браическое. Тогда система примет уп-

рощенный

вид

Рис.

1.46.

Фазовый

портрет

полной

системы (1.9—2)

(1.9-3)

(

\F(x,y)

Система уравнений

(1.9—3)

в отличие от полной системы

(1.9—2)

называется вырожденной.

Рассмотрим фазовый портрет полной системы

(1.9—2)

на рис.

1.46; напомним, что характер фазовых траекторий системы опре-

деляется расположением главных изоклин системы. Для системы

(1.9—2)

главные изоклины определяются уравнениями

G (х, у) -= О

— изоклина горизонтальных касательных и

F (х, у) = 0

— изоклина вертикальных касательных.

Точка их пересечения является особой точкой полной системы,

а ее координаты — стационарными значениями переменных х, у.

главах

4, 5 мы изучали метод линеаризации системы нели-

нейных

дифференциальных уравнений, позволяющий установить

характер устойчивости особой точки и поведение фазовых траек-

торий в малой окрестности особой точки. Здесь же рассмотрим

вопрос

о том, как влияет на общую

структуру

фазового портрета,

том числе и вдали от особой точки, наличие малого параметра

во втором уравнении системы (1.9—2). Важнейшей особенностью

фазового портрета этой системы

будет

наличие областей на пло-

скости х, у, резко отличающихся по скоростям изменения в них

переменных. В самом деле, фазовые траектории в любой точке

фазовой

плоскости, за исключением е-окрестности кривой F(x,y) =

0, имеют наклон, определяемый уравнением

dy __ G (х, у) .

dx F(x,y)

т. е. расположены почти горизонтально. Это так называемые об-

ласти быстрых движений, в которых вдоль фазовой траектории

у = const, а х быстро меняется. Достигнув по одной из таких гори-

зонталей е-окрестности кривой F(x, y)=0, изображающая точка

начнет затем двигаться по этой кривой. Скорость движения по го-

dx 1

ризонтальным участкам траектории = — = А, т. е. очень ве-

dt г

лика

по сравнению со скоростью движения в окрестности кривой

F(x,

г/)=0.

Поэтому общее время достижения некоего состояния

на

кривой F(x, y)=0 определяется характером движения вдоль

этой

кривой, т. е. фактически зависит лишь от начальных значе-

ний

медленной переменной у и не зависит от начального значения

быстрой переменной х.

Вырожденная система

(1.9—3)

содержит лишь одно дифферен-

циальное уравнение

— (х, У)

одно алгебраическое

F(x,y)

= 0,

задающее связь между переменными

хну.

Легко видеть,

что в

отличие

от

фазовой плоскости системы (1.9—2), через каждую

точку которой проходит фазовая траектория

(см. гл. 3),

плоскость

х,

вырожденной системы

(1.9—3)

содержит лишь одну кривую,

задаваемую уравнением

Из

любой точки, соответствующей начальным условиям х

, у

изображающая точка системы

(1.9—3)

скачком (у =

Уо

= const,

мгновенно меняется)

переходит

на кривую F(x, y)=0. Таким

образом, кривая стационарных значений переменной х вырожден-

ной

системы совпадает с изоклиной вертикальных касательных

полной

системы. В вырожденной системе

(1.9—3)

не отражаются

быстрые горизонтальные движения по фазовым траекториям пол-

ной

системы (1.9—2), которые, как мы уже установили, не оказы-

вают влияния на поведение системы на временах, характерных

для медленной переменной.

Посмотрим,

каковы условия, позволяющие заменять полную

систему уравнений вырожденной. Очевидно, для правомерности

такой

замены необходимо, чтобы независимо от начальных усло-

вий

изображающая точка полной системы быстро переходила на

изоклину

вертикальных касательных F(x, y)=0. Это означает, что

начальные условия х

должны попасть в область влияния устой-

чивой особой точки так называемого присоединенного уравнения

е—^- = F(x, у), поскольку особые точки I—

- = 0 ] этого уравнения

dt \ dt I

как

раз расположены на кривой F(x,

г/)=0.

Иными словами, не-

обходимо, чтобы решение х = х(у) алгебраического уравнения для

нахождения координат особой точки присоединенного уравнения

F(x, y)=0 было в то же время устойчивой изолированной особой

точкой этого присоединенного уравнения е = F (х, у) при

всех

значениях у, где у уже играет роль параметра.

В этом состоит основное содержание теоремы А. Н. Тихонова

(1952).

Приведем теперь

строгую

формулировку этой теоремы, кото-

рая

указывает условия, позволяющие проводить редукцию систе-

мы дифференциальных уравнений, т. е. замену дифференциальных

уравнений для быстрых переменных алгебраическими. Запишем

систему N уравнений, часть которых содержит малый параметр s

перед производной:

„ , ,

_ ..

~^ = F

... , x

Xr+u

... , x

(1.9-5)

Назовем

систему

(1.9—4)

присоединенной.

Соответствующая полной системе (1.9—4, 5) вырожденная си-

стема

будет

иметь вид

_ р / -.

гр \X\i • • •

i ^-г+Ь • • •

Xfj)

Теорема гласит следующее: решение полной системы (1.9—4, 5)

стремится к решению вырожденной при е->-0, если выполняются

следующие условия:

а) решение *i = (pi(xi, ..., x

), ..., х

= у

(х\, ..., x

) представляет

собой изолированный корень алгебраической системы

(х

.. . ,

А>,

г+и

. . . , x

) = 0 (р = 1, .. . , г)

(в

е-окрестности этого корня нет

других

корней);

4 Зак. 46 97

б) решение

, ..., х

—

устойчивая изолированная особая

точка присоединенной системы

(1.9—4)

при

всех значениях х

т+

и •••

...,

XJY;

в) начальные условия х\,

х°, . .. ,х°

попадают

область влия-

ния

устойчивой особой точки присоединенной системы;

г) решения полной

присоединенной системы единственны,

правые части непрерывны.

Число

начальных условий вырожденной системы меньше,

чем

полной:

начальные значения быстрых переменных

не

используют-

ся

вырожденной системе. Согласно теореме Тихонова, если

вы-

полняется

условие (в),

результат

не

зависит

от

начальных условий

для переменных присоединенной системы.

Мы

видим,

что

необходимым условием, позволяющим проводить

редукцию системы дифференциальных уравнений, является нали-

чие малого параметра

е в

уравнениях (1.9—4). Если

полной

си-

стеме уравнений имеются параметры разной степени малости,

теорему Тихонова можно применять несколько

раз

последователь-

но.

Сначала рассматривается вырожденная система

при

-*-0,

где

—

старшая степень параметра, затем исследуется вырожденная

система при

•е

-»-0

и так

по

убывающей степени параметра.

В уравнениях химической

биологической кинетики роль

ма-

лых параметров часто играют постоянные времени быстрых

про-

цессов различного порядка.

Это

позволяет анализировать поведе-

ние

сложных систем

на

различных промежутках времени,

что зна-

чительно облегчает

их

рассмотрение.

других

случаях

качестве

малого параметра выступает отношение малых концентраций

большим. Такая ситуация часто возникает

при

анализе фермента-

тивных процессов.

Теорема Тихонова широко используется

при

исследовании

сложных систем методом стационарных концентраций.

При

этом

сначала

на

основании экспериментальных данных обычно строится

вероятная схема, включающая довольно большое число перемен-

ных

разными характерными временами. Затем

помощью

пре-

дельного перехода

е->0

большая часть быстрых переменных

ис-

ключается. Простая система, содержащая оставшиеся медленные

переменные,

исследуется,

результаты сравниваются

экспери-

ментом.

Вернемся

нашей системе

из

двух

уравнений, одно

из

которых

описывает изменение

во

времени быстрой,

другое

—

медленной

переменной:

G(,y),^

F(,y) (.9)

Соответствующая

ей

вырожденная система имеет

вид

JiL=G(x,y), F(x,y) = 0. (I.9-3)

Кривая

F(x, y)=0

характеризует

для

вырожденной системы

(1.9—3)

зависимость стационарных значений переменной

х от па-

раметра у в отличие от полной системы (1.9—2), в которой х и и

являются равноправными переменными. Рассматривая уравнение

F(x, у) =0, можно легко сделать вывод о том

ка_кие из точек этой

кривой

соответствуют устойчивым решениям ~х=х(у) присоединен-

ного уравненияе-^-=

?(*,#),

где у — параметр. Вспомним, что

устойчивость точек этой кривой определяется знаком производной

Рх(х, У), причем те точки кривой F(x,

г/)=0,

в которых F

> 0,

являются неустойчивыми, а те, для которых

<0,

— устойчивы-

ми.

Изображающая точка в зависимости от знака производной

(x, У)

будет

быстро двигаться либо по направлению к квазиста-

ционарной

кривой при

<0,

либо от нее при F*>0 (рис 147)

Движение по самой кривой F(x, y)=0 есть медленное движение

оно происходит в соответствии с уравнением

Если

G(x, y)>0, то движение происходит вдоль Fix u)=0 так

что значения у

растут,

если же G(x, у) <0, то при движении у

уменьшается. Если F(x, «,)=<) представляет собой немонотонную

кривую, как это изображено на рис. 1.47, в точках изменения зна-

ка

производной F* (х, у) происходят скачки (точки А и В) В этих

точках происходит смена характеру устойчивости, так как в соот-

ветствии со знаком производной f'

(х, у) ветви СА и BD являются

устойчивыми, в то время как АВ — неустойчивой. По введенной

нами

в гл. 2 терминологии, точки А и В являются бифуркацион-

ными.

В соответствии со знаком JjL =

G(x,y)

изображающая точ-

ка

системы медленно

доходит

по ветви СА до точки А Дальше

по

кривой F(x, у)=0 изображаю-

щая

точка двигаться не может, У'

так

как ветвь АВ этой кривой яв-

ляется неустойчивой. Поэтому

система быстро переходит по го-

ризонтальной

изоклине AD на

устойчивую ветвь кривой

F{x, y)=0. Однако на этой вет-

ви

в соответствии со знаком

~гг = G(л;, г/)< О движение про-

исходит вниз в направлении точ-

ки

В, которая, так же как и точ-

ка

А,

будет

бифуркационной. Да-

лее снова

следует

быстрый го- • --

ризонтальный

скачок ВС. Затем точка движется по ветви СА. Та-

ким

образом, система совершает разрывные автоколебания по

замкнутой траектории — разрывному предельному циклу

ADBC.

Рис.

1.47. Фазовый портрет вырож-

денной системы (1.9—3). Особая точ-

ка

расположена на неустойчивой вет-

ви кривой F{x, у)—0

На

рис. 1.47 изображен случай, когда особая точка полной си-

стемы расположена на неустойчивой ветви АВ кривой F(x,

г/)=0.

Если же особая точка полной системы лежит на устойчивой ветви

кривой

F(x, у) = 0, то состояние равновесия устанавливается после

одного или нескольких колебаний. Вообще говоря, в каждом кон-

кретном

случае

поведение системы зависит от структуры, в особен-

ности от расположения особых точек полной системы, определяет-

ся

характером уравнений, описывающих как быстрые, так и мед-

ленные переменные, и

требует

каждый раз специального иссле-

дования.

Мы

видим, что в системе

переменную у можно рассматривать как управляющий параметр.

В связи с этим уместно провести аналогию с движением систе-

мы вдоль кривой стационарных состояний, рассмотренным в гл. 2

(см.

рис. 1.9). Мы видели, что при изменении управляющего пара-

метра а системы

(1.2—14)

с одним неизвестным х проходит через

ряд стационарных состояний, совершая в

результате

гистерезис-

ный

цикл. В системе (1.2—14), имеющей вид

где а — параметр, не задано в явном виде изменение во времени

величины а, в

результате

которого, собственно, и происходит дви-

жение по кривой стационарных состояний х = х(а) (рис. 1.9). Для

полного описания этого движения необходимо задать отдельное

независимое уравнение вида

-£-

= Ф<а,*), (1.9-7)

описывающее изменение а во времени за

счет

неких сил, внешних

по

отношению к системе (1.9—6).

Уравнения

(1.9—6)

(1.9—7)

образуют

вместе систему

двух

уравнений с

двумя

неизвестными х, а:

Исходя из описанных выше свойств полной системы

(1.9—8)

легко заключить, что скорость изменения а во времени в уравнении

(1.9—7)

должна быть значительно меньше скорости изменения х

(1.9—6), т. е.

ф(а,

*)«/(*, а).

(1.9—9)

100