Розенберг Л.Д. Физика и техника мощного ультразвука. Книга 1. Источники мощного ультразвука OCR
Подождите немного. Документ загружается.


имеет
вид
[131
Ф(
)
_
(1-n)(соsсх-n)J/2
а
-
3/'
(1-
n
coscx)
2
(15)
и
соответственно
для
предельного
случая
n =
О
(материал
линзы
с
очень
большой
скоростью
распространения
звука):
(15а)
Наконец,
для
параболического
вогнутого
зеркала
[2]
без
учета
потерь
на
отражение:
Ф
(
)
_ 1 + cos
сх
а
- 2 .
(16)
Для
выбора
наиболее
эффективной
системы
фокусирования
сравним,
например,
давление
в
центре
фокального
пятна
при
одинаковом
потоке
энергии
(мощности),
несомой
фронтом
сходящейся
волны.
Как
уже
го
ворилось,
можно
считать,
что
каждый
небольшой
участок
фронта
излу-
р2
чает
плоскую
волну
интенсивностью
10'
где
1
о
=
-2
о
•
Весь
поток
энер
РОС
гии
будет
равен,
таким
образом,
СХ
т
р2
•
W=2лF2_20
~.
ф2
(а)
sinada.
РоС
J
о
Давление
и
скорость
в
центре
фокальной
области
в
соответствии
с
выражениями
(2а)
и
(13)
равны
и
СХ
т
PF=kFpo~
Ф(а)siпаdа
о
СХ
т
ир
= kFvo
~
Ф
(а)
cos
а
sin
а
аа.
о
Отбрасывая
постоянные,
не
зависящие
от
вида
функции
Ф
(а)
множи
тели,
получим
следующую
математическую
формулировку
задачи
о
наи
выгоднейшем
распределении
заданной
мощности
по
поверхности
волнового
фронта
для
получения
наибольшей
величины
давления
или
колебательной
скорости
в
центре
фокального
пятна:
найти
функции
Ф
(а),
приводящие
к
наибольшим
значениям
интегралов
~т
Ф
(,,)
sin"
а"
о
п:
СХ
т
~
Ф(а)соsаsiпаdа,
о
при
сохранении
постоянства
величины
интеграла
~rn
j
ф2
(а)
sin
а
аа.
о
11
ИСТОЧНИНИ
ультразвуна
:16:1

Эта
задача
на
так
называемый
условный
экстремум
решается
обычными
методами
вариационного
исчисления.
Оказывается,
что
для
получения
наибольшего
давления
в
центре
фокального
пятна
нужно
иметь
Ф
(а)
= 1,
(17)
т. е.
энергию
нужно
распределить
по
поверхности
фронта
равномерно,
тог
да
как
для
получения
наибольшей
колебательной
скорости
Ф
(а)
=
cosa.
(18)
Как
видим,
условия
наибольшей
концентрации
давления
и
скорости
J:f.e
совпадают.
Физический
смысл
условий
(17)
легко
понять,
если
учесть~
QTO
sin
ctda
есть
элемент
сферической
поверхности
единичного
радиуса~
т. е.
что
интересующие
нас
интегралы
могут
быть
записаны
в
виде
и
Тогда,
рассматривая
интегралы
как
пределы
соответствующих
сумм,
мож
но
свести
поставленную
задачу
к
следующей:
определить
совокупность
величин,
сумма
членов
которой
имеет
наибольшее
значение
при
заданной
сумме
их
квадратов.
Из
элементарных
соображений
ясно,
что
наибольшее
значение
эта
сумма
будет
иметь
при
условии
равенств
всех
ее
членов.
Что
касается
условия
(18),
то
надо
принять
во
внимание
следующие
соображения:
чем
больше
тот
угол
а,
под
которым
приходит
энергия
к
фокальному
пятну,
тем
меньше
ее
вклад
в
увеличение
скорости,
так
как
в
этом
участвует
лишь
осевая
компонента.
Поэтому
выгодно
в
центральной
части
фронта
сосредоточить
больше
мощности,
а
на
краях
меньше.
Как
будет
видно
из
дальнейшего,
условие
(18)
не
очень
критично;
например,
функция
cos'/2a
дает
почти
такие
же
результаты.
Нужно
сказать,
что
при
не
очень
больших
углах
а,
не
превышающих
а
< 450,
cosa
отличается
от
единицы
всего
на
30%
и
условия
(17)
и
(18)
практически
совпадают.
Различие
наступает
лишь
при
углах,
приближа
ющихся
к
900.
Прежде
чем
перейти
к
дальнейшему
анализу
оптимальных
УСЛОВИЙ
t
следует
обратить
внимание
на одно
простое
соотношение,
имеющее
место
также
при
не
очень
больших
углах
а
т
•
Сопоставим
выражения
(3а)
и
(6а):
лF
r
o
= 0,61
Я'
Их
произведение
дает
постоянную
величину,
зависящую
лишь
от
ра
диуса
входного
зрачка
системы:
Kpro
=
1,92·R.
Другими
словами,
уменьшение
радиуса
кружка
Эри
влечет
за
собой
увеличение
коэффициента
усиления,
и
наоборот.
Возведя
в
квадрат
и
несколько
видоизменив
это
выражение,
получим
2
R2
К
р
=3,7-
2
•
Г
О
Но
для
малых
углов-раскрытия
к;
= K
r
,
поэтому
получаем
1 F
'ЛД
2
К
!
=
т
=
3,7
--2
.
О
ЛГ
о
1.62

Это
соотношение
можно
было
бы
написать
и
а
priori,
так
как
оно
выте
кает
из
закона
сохранения
энергии:
интенсивности
в
исходной
волне
и
в
центре
фокального
пятна
обратно
пропорциональны
соответствующим
площадям.
Множитель
3,7
учитывает
то,
что
интенсивность
в
центре
фо
кального
пятна
больше
средней
интенсивности
по
всей
его
поверхности,
а
также
то,
что
через
фокальное
пятно
проходят
не
все
100%
фокусируемой
энергии,
а
лишь
84%,
а
16%
падает
на
долю
вторичных
максимумов.
§
5.
Фактор
фокусировании
Перейдем
теперь
к
нахождению
наибольшей
величины
звукового
дав
ления,
которое
можно
получить,
имея
оптимальную
функцию
распределе
ния
при
заданной
величине
полного
потока
энергии
фронта.
Для
этого
рассмотрим
последовательность
волновых
фронтов
с
поверхностью
S
с
равномерным
распределением давления
по
поверхности,
различными
угла
ми
раскрытия
(Х,т
И
соответственно
различными
радиусами
кривизны
(фо
кусными
расстояниями)
F.
Одинаковость
поверхностей
фронтов
при
ра
венстве
давлений
Ро
соответствует
равенству
полных
потоков
энергии.
Введем
понятие
эквивалентного
радиуса
фронта
R
э
,
определяемого
из
соотношения
s =
лR~.
(19)
Теперь
будем
изгибать
этот
фронт
по
сфере
уменьшающегося
радиуса
F
при
соответственно
увеличивающемся
угле
раскрытия
(х'т'
"Учитывая,
что
S =
2лF2
(1
- COS(X,m),
получим
(20)
Подставляя
значения
(19)
и
(20)
в
(3а)
,
найдем
коэффициент
усиления
по
давлению
при
постоянной
поверхности
фронта
(21)
При
(Х,т
=
Л
выражение
(21)
достигает
максимума,
который
равен
К
р
,
шах
=
kR
э
•
(22)
Это
и
есть
тот
наибольший
коэффициент
усиления,
который
можно
полу
чить
при
самых
оптимальных
условиях:
Ф
((Х,)
= 1,
(Х,т
=
Л.
Интересно
отметить,
что
это
выражение
совпадает
с
так
называемым
коэффициентом
концентрации
плоского
поршневого
излучателя
радиуса
а,
который,
как
известно,
равен
ka.
Разница
заключается
в
том,
что
у
поршня
этот
коэф
фициент
может
быть
достигнут
лишь
на
большом
расстоянии
L,
опреде
ляемом
из
условия
на
котором
интенсивность
звука
успевает
уменьшиться
в
L2
по
сравнению
с
10'
тогда
как
в
случае
сходящегося
сферического
фронта
он
реализуется
на
малом
расстоянии
F
и
приводит
К
усилению
интенсивности.
Естественно
оценивать
усиление
той
или
иной
системы,
относя
ег.о
и
:максимально
возможному
значению.
Так,
для
фронта
с
равномерным
рас
пределением
амплитуды,
который
может
быть
получен
при
помощи
сфери-
11
*
:163

ческого
фокусирующего
излучателя,
например,
из
радиально
поляризо
ванной
пьезоэлектрической
керамики,
это
отношение
будет
К
р
К
р
•
а
т
К
=
kR
=sш
2
·
р,
шах
э
(23)
Назовем
его
фактоl'ОМ
фокусирования
и
будем
в
дальнейшем
обозна
чать
через
%.
Фактор
фокусирования
-
это
функция
угла
раскрытия,
причем
вид
ее
определяется
функцией
распределения
Ф
(сх),
или,
другими
словами,
типом
фокусирующей
системы.
Для
сравнения
фактора
фокуси
рования
различных
типов
систем
следует
сначала
установить,
что
считать
эквивалентным
радиусом
при
неравномерном
распределении
ам
плитуды
на
поверхности
сходящегося
фронта.
х
1,0
0,8
О,б
0,4
0,2
О
/
80
100
Рис.
8.
3ависимость
фантора
фонусирова
ния
давления
%
от
угла
раснрытия
а
т
для
различных
типов
фонусирующих
систем
l-фОНУСИРУЮЩИЙ
нерамичесний
излучатель;
2-
вогнутое
параболичесное
зернало;
а
-
вогнутая
собирающая
линза;
4 -
выпунлая собирающая
линза;
5 -
оптимальный
фронт
для
получения
наибольшей
нонцентрации
снорости
Так
как основным
условием
сравнения
является
постоянство
потока
энергии
фронта,
то
R
э
найдется
из
соотношения
откуда
ОСт
лR~
=
2лF2
~
ф2
(а)
sin
а
аа,
о
ос
rn
1/2
R
э
=F(2
~
ф2(а)siпаdа)
о
(19а)
в
тех
случаях,
когда
мы
имеем
дело
с
пассивным
концентратором
(зер
кало,
линза),
питающимся
от
плоского
излучателя,
R
э
-
радиус
вход
ного
зрачка,
равный
радиусу
излучателя,
F -
его
фокусное
расстояние,
а
Ро-
давление
в
плоскости
входного
зрачка
(если
считать,
что
в
концен
траторе
совершенно
отсутствуют
потери).
На
рис.
8
показаны
зависимости
фактора
фокусирования
от
угла
рас
крытия
а
т
для
фокусирующего
керамического
излучателя
1,
вогнутого
параболического
зеркала
2,
вогнутой
собирающей
линзы
(е
показателем
преломления
n=О)
3,
выпуклой
собирающей
линзы
(при
n = 00) 4
и
опти
мального
фронта
для
получения
наибольшей
концентрации
скорости
б.
Последний
случай
может
быть
приближенно
реализован
при
помощи
фону
сирующего
излучателя
из
аксиально
поляризованной
керамики
(рис.
9).
Нормальная
скорость
на
поверхности
излучателя
изменяется
по
закону,
близкому
к
cos
а.
При
изготовлении
такого
излучателя
следует
еще
учесть,
что
толщина
его
должна
уменьшаться
от
середины
к
краям,
чтобы
на.всех
участках
сохранялись
условия
толщинного
резонанса
пластинки.
Из
рис.
8
видно,
что
до
углов
80-850
все
типы
фонусирующих
систем
ведут
себя
приблизительно
одинаково;
различия
начинают
сказываться,
когда
сх.
т
> 800.
В
большинстве
практических
случаев
угJШ
раскрытия
не
превышают
800,
так
как при
этом
фокальная
область
еще
лежит
за
пределами
среза
концентратора,
что
очень
облегчает
манипулирование
при
работе
с
ним.
В
этом
диапазоне
углов
сх.
т
можно
считать
о
а
т
Х
= 120 '
а
для
крайнего
значения
сх.
т
= 800,
х
= 0,67.
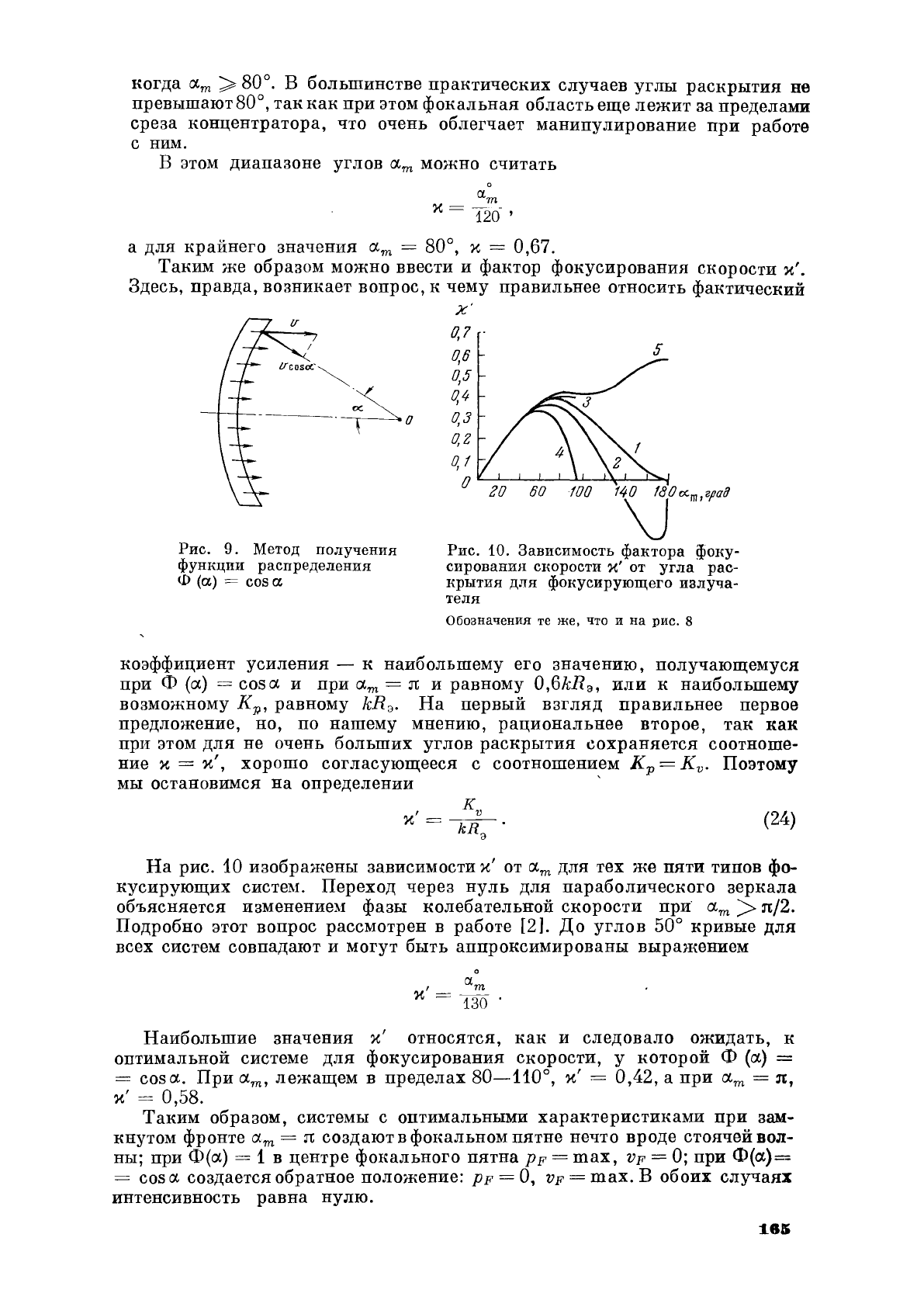
Таким
же
образом
можно
ввести
и
фактор
фокусирования
скорости
х'.
Здесь,
правда,
возникает
вопрос,
к
чему
правильнее
относить
фактический
Рис.
9.
Метод
получения
функции
распределения
Ф
(а)
=
сова
)СО
0,7
0,8
0,5
0,4
0,3
о,г
0,1
5
IJ
L--zJ...o--'--8J...о--'-...J-!Оцo----1~f.,-l\J-о~t.~'8
О
оСт,
гро8
Рис.
10.
Зависимость
фаRтора
фоку
сирования
СRОРОСТИ
х'
от
угла
рас
крытия
для
фОRусирующего
излуча
теля
Обозначения
те
же,
что
и
на
рис.
8
коэффициент
усиления
-
к
наибольшему
его
значению,
получающемуся
при
Ф
(сх.)
= cos
сх.
и
при
сх.
т
= n
и
равному
0,6kR
э
,
или
к
наибольшему
возможному
К
р
,
равному
kR
э
•
На
первый
взгляд
правильнее
первое
предложение,
но,
по
нашему
мнению,
рациональнее
второе,
так
как
при
этом
для
не
очень
больших
углов
раскрытия
сохраняется
соотноше
ние
х
=
х',
хорошо
согласующееся
с
соотношением
К
р
= K
v
•
Поэтому
мы
остановимся
на
определении
(24)
На
рис.
10
изображены
зависимости
х'
от
сх.
т
для
тех
же
пяти
типов
фо
кусирующих
систем.
Переход
через
нуль
для
параболического
зеркала
объясняется
изменением
фазы
колебательной
скорости
при'
сх.
т
>
п/2.
Подробно
этот
вопрос
рассмотрен
в
работе
[2J.
До
углов
500
кривые
для
всех
систем
совпадают
и
могут
быть
аппроксимированы
выражением
о
,
а
т
Х
= 130 .
Наибольшие
значения
х'
относятся,
как
и
следовало
ожидать,
к
оптимальной
системе
для
фокусирования
скорости,
у
которой
Ф
(сх.)
=
= cos
сх..
При
сх.
т
,
лежащем
в
пределах
80-1100,
х'
= 0,42,
а
при
сх.
т
=
п,
х'
= 0,58.
Таким
образом,
системы
с
оптимальными
характеристиками
при
зам
кнутом
фронте
сх.
т
= n
создают
в
фокальном
пятне
нечто
вроде
стоячей
ВQJI
ны;
при
Ф(сх.)
= 1
в
центре
фокального
пятна
PF
=
шах,
VF
=
О;
при
Ф(сх.)=
=
coscx.
создается
обратное
положение:
PF
=
О,
VF
=
шах.
В
обоих
случаях
интенсивность
равна
нулю.
.85
Остается
выяснить
оптимальное
соотношение
для
получения
бегущей
волны,
которые,
очевидно,
соответствуют
условию
PFVF
=
шах.
Последнее
выражение
эквивалентно
условию
%.
%'
=
шах.
Как
легко
видеть
из
соотношений
(На),
(23)
и
(24),
для случая
Ф
(сх)
= 1
,
sin
2
cx
произведение
%.
'Х,
равно
~
и
достигает
максимума,
равного
0,25
при
СХ
m
=л/2;
этот
максимум
не
слишком
критичен:
при
изменении
СХ
m
на
+
100
величина"произведения
падает
на
3%,
при
изменении
на
+
150
-
на
6 %,
а
при
200
-
на
12
% . -
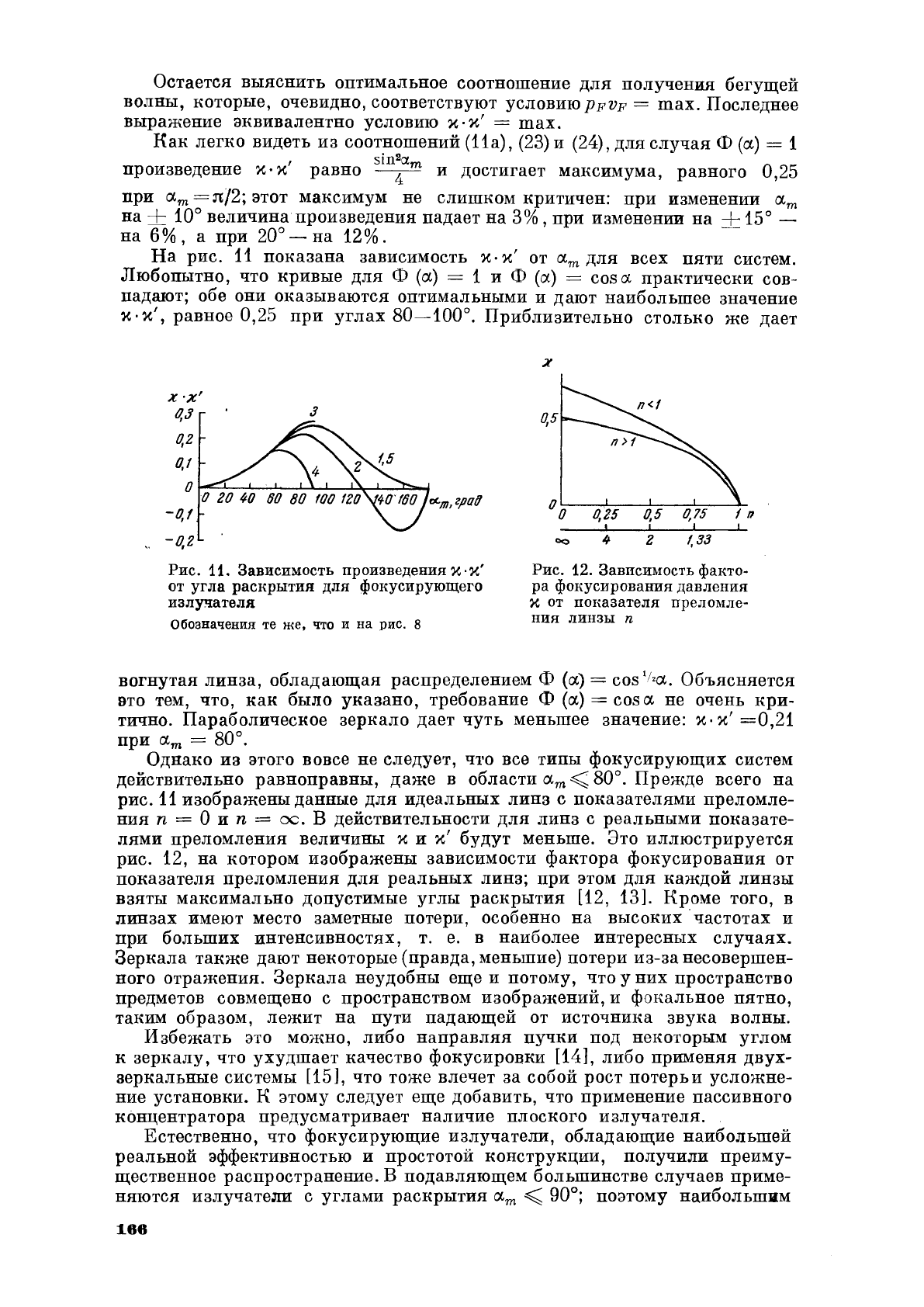
На
рис.
11
показана
зависимость
'Х,.
'Х,'
ОТ
СХ
m
для
всех
пяти
систем.
Любопытно,
что
кривые
для
Ф
(сх)
= 1
и
Ф
(сх)
=
COSCX
практически
сов
падают;
обе
они
оказываются
оптимальными
и
дают
наибольшее
значение
'Х,.
'Х,',
равное
0,25
при
углах
80-1000.
Приблизительно
столько
же
дает
Х'х'
0,3
и,г
0,1
-и,!
-о,г
J
Рис.
11.
Зависимость
произведения
'Х,''Х,'
от
угла
раскрытия
для
фокусирующего
излучателя
Обозначения
те
же,
что
и на
рис.
8
о
о
0,25 0,5
0,75
, I I
z
1,99
Рис.
12.
Зависимость
факто
ра
фокусирования
давления
'Х,
от
показателя
преломле
ния линзы
n
вогнутая
линза,
обладающая
распределением
Ф
(сх)
= COS
1/·
сх
.
Объясняется
это
тем,
что,
как
было
указано,
требование
Ф
(сх)
= COS
сх
не
очень
кри
тично.
Параболическое
зеркало
дает
чуть
меньшее
значение:
'Х,.
'Х,'
=0,21
при
СХ
m
=
800.
Однако
из
этого
вовсе
не
следует,
Чl'О
все
типы
фокусирующих
систем
действительно
равноправны,
даже
в
области
СХ
m
-<
800.
Прежде
всего
на
рис.
11
изображены
данные
для
идеальных
линз
с
показателями
преломле
ния
n =
О
и
n =
ос.
В
действительности
для
линз
с
реальными
показате
лями
преломления
величины
'Х,
и
'Х,'
будут
меньше.
Это
иллюстрируется
рис.
12,
на
котором
изображены
зависимости
фактора
фокусирования
от
показателя
преломления
для
реальных
линз;
при
этом
для
каждой
линзы
взяты
максимальНо
допустимые
углы
раскрытия
[12, 13].
Кроме
того,
в
линзах
имеют
место
заметные
потери,
особенно
на
высоких"
частотах
и
при
больших
интенсивностях,
т.
е.
в
наиболее
интересных
случаях.
Зеркала
также
дают
некоторые
(правда,
меньшие)
потери
из-за
несовершен
ного
отражения.
Зеркала
неудобны
еще
и
потому,
что
у
них
пространство
предметов
совмещено
с
пространством
изображений,
и
фокальное
пятно,
таким
образом,
лежит
на пути
падающей
от
источника
звука
волны.
Избежать
это
можно,
либо
направляя
пучки
под
некоторым углом
к
зеркалу,
что
ухудшает
качество
фокусировки
[14],
либо
применяя
двух
зеркальные
системы
[15],
что
тоже
влечет
за
собой
рост
потерьи
усложне
ние
установки.
К
этому
следует
еще
добавить,
что
применение
пассивного
концентратора
предусматривает
наличие
плоского
излучателя.
Естественно, что
фокусирующие
излучатели,
обладающие
наибольшей
реальной
эффективностью
и
простотой
конструкции,
получили
преиму
щественное
распространение.
В
подавляющем
большинстве
случаев
приме
няются
излучатели
с
углами
раскрытия
СХ
m
<
900;
поэтому
наиБОЛЬШJlМ
1.66

распространением
пользуются
наиболее
простые
системы
с
Ф
(<Х)
= 1,
т.
е.
вогнутые
излучатели
из
радиаЛЬElО
поляризованной
пьезоэлектри
ческой
керамики.
Б.
Цилиuдрuчесuuе
uз.rtучаmе.rtu
Цилиндрические
фокусирующие
излучатели,
т.
е.
такие
излучатели,
которые
создают
когерентный
синфазно
сходящийся
цилиндрический
фронт,
дают
меньшую
концентрацию
энергии,
чем
сферические,
так
как
собира
ют
энергию
в
фокальной
полосе,
оеь
которой
совпадает
с
осью
сходящегося
фронта.
Длина
этой
полосы
приблизительно
равна
длине
образующей
излу
чателя.
Такой
тип
фокусирования
имеет
свои
преимущества
и
применя
ется,
например,
в
процессах
ультразвуковой
очистки,
поточной
обработ
ки
жидкостей и
т.
д.
§
8.
ЦИa1IипдрическиА
фронт
бесконечноlI
Дa1IИНЫ
Рассмотрим
случай
цилиндрического
фронта
бесконечной
длины
с
рав
номерным
распределением
амплитуды.
В
приближении
Кирхгофа,
считая,'
что
фокусное
расстояние
F
велико
по
сравнению
с
длиной
волны
Л,
можно
воспользоваться
одночленной
формулой
Грина
[16]
для
выражения
потен
циала
скоростей
ер
в
двумерной
области:
i \ (2)
ер
=
"2
J
voHo
(kp) dl,
с
где
vo-
нормальная
скорость
на
поверхно
сти
фронта;
k -
.волновое
число;
dl
-
эле
мент
поверхности
дуги
фронта;
р
-
расстоя
ние
от
произвольной
точки
поверхности
фрон
та
до
точки
наблюдения;
с
-
контур
повер-
хности
интегрирования;
Нь
2
)-функция
Хан
келя
второго
рода
нулевого
порядка.
Из
рис.
13
ясно,
что
если
обозначить
по
лярные
координаты
точки
приема
через
ro
и
ао,
то
р
= F
[1
+ (
~
)2
- 2
~
cos
(<Х
-
<Хо)
Т'
.
-0(.,,/
I
/
/
I
Рис.
13. R
ВЫВОДУ
усиления
цилинДрического
схоДящегося
фронта
Вдали
от
поверхности
излучателя
можно
воспользоваться
асимптотическим
представлением
функции Ханкеля
и
переписать
интересующий
нас
инте
грал
в
виде
(25)
Вблизи
цилиндра,
в
фокальной
области,
где
можно
считать
F >
л,
выраже
ние
(25)
упр
ощается
и
переходит
в
(25а)
:167

8<р
,
8<р
б
Ф
u
Помня,
что
Р
=
Р
7ft'
а
V = -
az
'
и
от
расывая
азовыи
множи-
тель,
получим
окончательно
для
окрестности
фокальной
линии
+ot
m
Р
= (
~~
)
1/.
~
eikro
сов
('%-(10)
аа,
-ОСт
+ot
m
V = (
~~
У/2
~
eikro
cos
(cx-oto)
COS
(а
-
(хо)
аа.
-ОСт
(26)
(27)
в
центре
фокального
пятна
ro
=
О,
(хо
=
О,
и
выражение
для
давления
и
скорости
[17]
перейдет
в
(
2kF
)1/.
Р
р
=
РО
----п-
(х
т
,
(26а)
(
2kF
)1/2
. , d
VF
= Vt)
п-
slnrx
r:t.,
(27а)
а
соответствующие
коэффициенты
усиления
запишутся
как
(28)
(29)
(30)
Как
и
для
сферических
излучателей,
К
р
максимально
при
(х
т
=
л,
тогда
как
К,!),
пройдя
через
максимум
при
(х
т
=
'Л/2,
обращается
при
(х
т
=
'л
В
нуль.
При
малых
углах,
когда
sin
(х
т
~
(х
т
,
К
р
= K
v
·
Рассмотрим
теперь
оптимальные
соотношения.
Для
цилиндрических
систем
характерной
величиной
является
поток
энергии
на
единицу
осевой
длины
фронта.
Поэтому
условием
постоянства
потока
энергии
является
постоянство
длины
фронта
L
по
образующей:
L =
2Frx
т
.
(31)
С
учетом
этого
выражения
(28,)
и
(29)
можно
переnисать
в
виде
(28а)
(29а)
Максимально
возм
ожный
коэффициент
усиления
по
давлению
получит
ся
при
(х
т
=
'л
И
величина
его
1/
К
р
тах
= (kL)
2.
(28б)
Тогда
для
цилиндрического
фронта
с
равномерным
распределением
ампли
туды
фактор
фокусирования
по
давлению
будет
равен
(32)
188
а
по
скорости
, K
v
% =
"-;0"::----
-
K
v
•
шах
(33)
Величина,
характеризующая
концентрацию
интенсивности,
будет
равна
sin
сх
т
%.%'
=---
n
и
проходит
через
максимум,
равный
1/'Л
при
а
т
=
'Л/2.
х
1,0
0,5
о
ZO
50 /00 /40
/BO«m
х'
,
;к·х'
0,5
0,4
0,3
о,г
0,1
о
/
v
('
го
L
80
(34)
z
-~
~
".
~
3
~
100
140\
у;,
\1/
Рис.
14.
Зависимость
факторов
фокусирова
ния
давления
%
и
скорости
%'
для
различных
случаев
цилиндрического
фокусирования
1 -
Ф(а)
= 1
(радиально
ПОЛЯРИЗ0ванный
излуча
тель);
2-Ф
(a)=cos
а
(ансиально
ПОЛЯРИЗ0ванный
нерамичесний
излучатель);
3 -
Ф
(а)=
(сов
а!2)-1
(цилиндричеСRое
параболичеСRое
зернало)
Рис.
15.
Зависимость
величины
%-%'
от
угла
раскрытия
СХ
т
для
радиально
поля
ризованного
цилиндрического
излуча
теля
При
неравномерном
распределении
амплитуды
по
фронту
сходящейся
волны
коэффициенты
усиления
описываются
формулами,
аналогичными
(12)
и
(13):
(35).
<Х
т
(
2kF
)1/
С'
K
v
=
-л
2 J
Ф(а)соsаdо:,
(36)
о
где
Ф
(а)
-
функция
распределения,
симметричная
относительно
точки
а
=
О.
Задача
о
нахождении
оптимального
распределения
при
сохранении
постоянного
потока
энергии
через
единицу
длины
фронта,
равного
(37}
имеет
то
же
решение,
что
и для
осесимметричного
фронта:
для
получения
наибольшего
давления
оптимальное
распределение
Ф
(а)
= 1,
для
полу
чения
наибольшей
скорости:
Ф
(а)
= cos
а.
В
случае
фокусирования
плоской
волны
цилиндрическим
параболиче
ским
зеркалом
функция
распределения
будет
[17]:
Ф
(а)
= cos-
1
~
•
(38)
1.
...

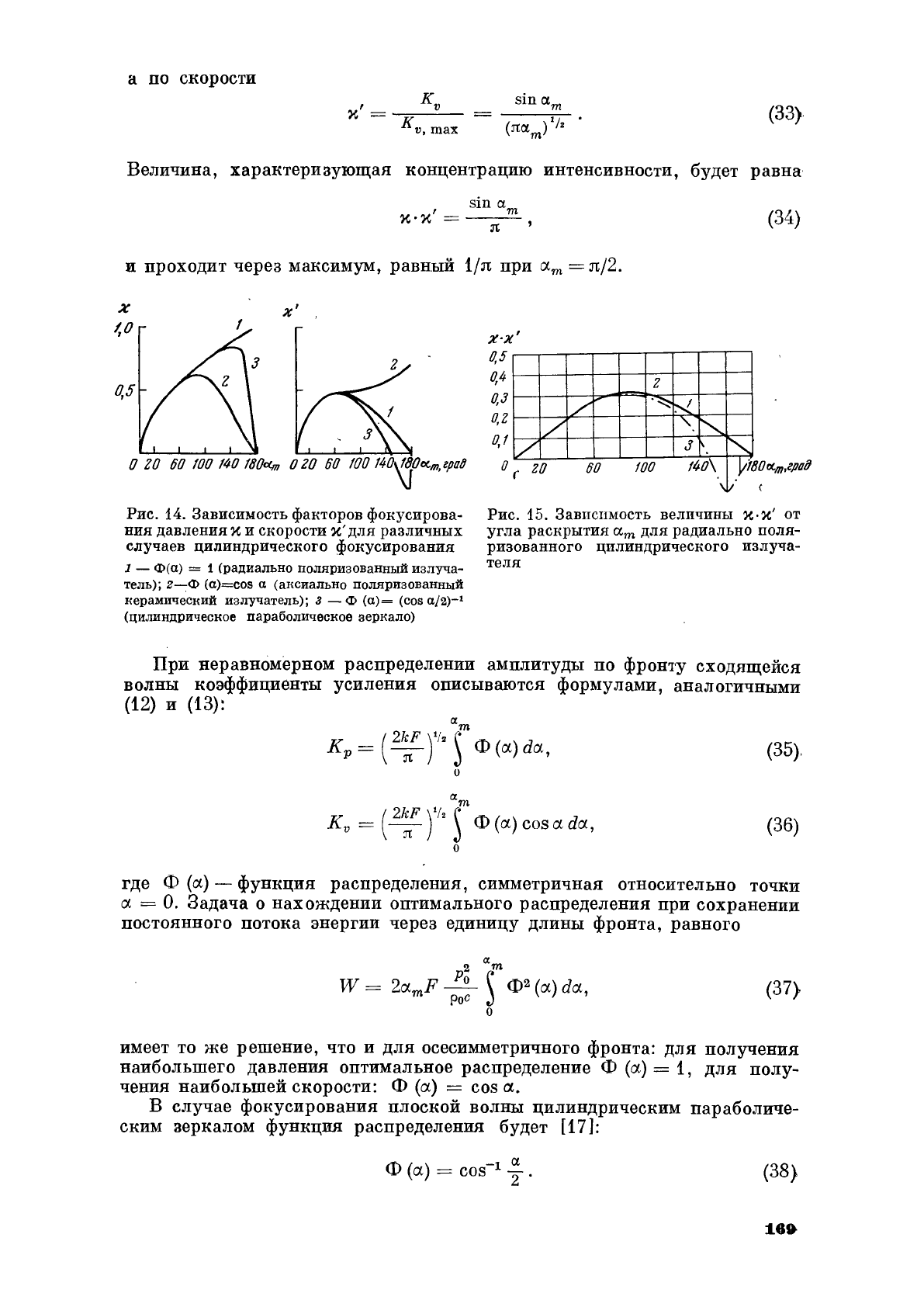
На
рис.
14
изображены
зависимости
хи
х'
от
а
m
для
трех
практически
наиболее
интересных
случаев,
а
на
рис.
15
-
зависимость
х·
х'.
Сопостав
ление
этих
кривых
с
соответствующими
данными
для
осесимметричных
сис
тем
(см.
рис.
8, 10,
11)
показывает
большое
качественное
сходство
с
последними;
разница
лишь
в
количественных
соотношениях.
§
7.
ЦИ.JIиндричесииЙ
фронт
конечной
Д.JIИПЫ
Не
следует
забывать,
что
все
полученные
соотношения
относятся
к
цилинд
рическому
фронту
бесконечной
длины, для
которого
справедлива
только
трактовка
рассматриваемой
задачи
как
двухмерной.
В
действительности
нам
всегда
приходится
иметь
дело
с
излучателями,
а
следовательно,
и
с
фронтами
конечной
длины.
Это
обстоятельство
будет
учтено
несколько
ни
же,
а
здесь
мы
ограничимся
оцеНFl)Й
влияния
конечности
длины
фронта
-{
о
f z
Рис.
16.
Распределение
oceBoro
дав
ления
в
цилиндричеСI\ОМ
фокусирую
щем
излучателе
конечной
длины
на
величину
давления
на
оси
или
(что
то
же
самое)
на
коэффициент
усиле·
ния
по
давлению.
Из
самого
факта
осевой
симметрии
сходящегося
синфазного
фронта
следует,
что
соотношение
между
полем
конечного
и
бесконечного
цилин
дрического
фронтов
с
произвольным:
распределением
Ф
(а)
будет
такое
же,
как
между
полем
конечного
(той
же
длины)
и
бесконечного
линейного
синфазного
источников,
лежащих
вдоль
произвольной
образующей
цилин·
дра
на
расстоянии
F
от
точки
наблюдения.
Последнее
соотношение
может
легко
быть
получено
из
хорошо
извест
ных
выражений,
например
для
дифраRЦИИ
на
щели
конечных
размеров
[19 J •
Для
амплитуды
оно имеет
вид
(39)
u
и
где
\'
:rtv
2
\'
:rtv
2
С
(и)
=
.)
cos
-2-
аи;
S
(и)
= J
sin
2-
аи
-
интегралы
Френеля;
u
о
}f2y
u u
U =
"1/-
,
а
Уl
и
У2
-
расстояния
от
проекции
ТОЧRИ
приема
на
линеиныи
J'
лF
источник
(или
его
продолжение)
до
концов
источника.
Для
учета
влия
ния
одного
ИЗ
концов
предположим,
что
другой
находится
очень
далеко
и
не
оказывает
никаRОГО
влияния;
справедливость
такого
предположения
будет
видна
в
ходе
дальнейшего
анализа.
Тогда
У2
=
00,
и2
=
ОС,
С(::ю)
=:S(oo)
=
1/2
И
(39а)
Последнее
соотношение
изображено
на
рис.
16,
где
по
оси
абсцисс
от
ложена
величина
и/У2
=
у/
VлF
-
безразмерная
дl
ина
у,
выраженная
в
:1'70
