Розенберг Л.Д. Физика и техника мощного ультразвука. Книга 1. Источники мощного ультразвука OCR
Подождите немного. Документ загружается.


г
JI
а
в
а
;1
ГАаОСТРУilныil
иаЛУЧАТЕЛЬ
ГАРТМАНА
§
1.
Истечение
гцза
из
СОПoJIа
Генерация
звуко.вых
ко.лебаний
в
излучателях
гартмано.вско.го.
типа
тесно.
связана
с
эффектами,
во.зникающими
в
сверхзвуко.вых
струях.
По.это.му
для
лучшего.
по.нимания
про.цессов,
про.исхо.дящих
в
газо.струй
ных
излучателях,
мы
кратко.
о.стано.вимся
на
о.со.бенно.стях
струи,
ско.ро.сть
ко.то.ро.й
превышает
ско.ро.сть
звука.
Если
в
струе,
движущейся
со.
ско.ро.стью,
меньшей
ско.ро.сти
звука
(До.
;шуко.во.е
течение),
во.зникшие
во.змущения
мо.гут
распро.страняться
в
лю
бо.м
направлении
(их
ско.ро.сть
равна
ско.ро.сти
звука),
то.
в
сверхзвуко.во.м
по.то.ке
во.змущения
мо.гут
двигаться
либо.
по.
по.то.ку,
либо.
в
неко.то.рых
направлениях,
о.пределяемых
ко.нусо.м
во.змущений
(ко.нусо.м
Маха).
Си
нус
по.ло.винно.го.
угла
при
вершине
это.го.
ко.нуса
о.пределяется
о.тно.ше
нием
ско.ро.сти
звука
к
ско.ро.сти
по.то.ка.
Распро.странение
во.змущений
по.д
углами,
превышающими
уго.л
Маха,
нево.змо.жно.,
так
как
во.змущения
сно.сятся
по.то.ко.м.
По.это.му
движение
газа
при
до.звуко.вых
и
сверхзвуко.
ных
ско.ро.стях
существенно.
различно..
Следует
о.тметить,
что.
если
в
акустике
ско.ро.сть
звука
с
в
о.пределенно.й
среде
считается
по.сто.янно.й
в
про.странстве
и
зависит
лишь
о.т
абсо.лютно.й
температуры,
то.
в
сверхзвуко.во.м
по.то.ке
-
это.
величина
не
по.сто.янная
и
меняется
о.т
то.чки
к
то.чке,
в
зависимо.сти
о.т
местных
значений
давления
и
пло.тно.сти
газа.
Таким
о.бразо.м,
мо.жно.
го.во.рить
О.
местно.й
ско.ро.сти
зву-
ка,
по.дразумевая
по.д
этим,
как
и
в
акустике,
величину
с
=
V(dpjdp)s,
где
р-давление,
а
р
-
пло.тно.сть
газа.
Индекс
s
указывает
на
изо.энтро.
пично.сть
про.цесса.
В
гидро.динамике
ско.ро.сть
газа принято.
характери
ао.вать
о.тно.шением
абсо.лютно.й
ско.ро.сти
по.то.ка
в
данно.й
то.чке
к
местно.й
ско.ро.сти
звука.
Это.
о.тно.шение
но.сит
название
числа
Маха
и
о.бо.значается
букво.й
М.
Таким
о.бразо.м,
при
М
< 1
по.то.к
о.казывается
до.звуко.вым,
а
при
М
> 1 -
сверхзвуко.вым.
Из
сказанно.го.
следует,
что.
сверхзвуко.во.й
по.то.к
о.бладает
интерес
ным
сво.Йство.м.
По.ско.льку
во.змущения
не
мо.гут
двигаться
про.тив
по.то.ка
газа,
то.
при
введении
в
струю
препятствия
течение
вверх
по.
по.то.ку
не
ме
няется
(струя
(<Не
знает»
о.
то.м,
что.
по.явило.сь
препятствие);
изменение
течения
имеет
место.
то.лько.
вниз
по.
по.то.ку.
Сверхзвуко.во.й
по.то.к
имеет
еще
о.дно.
о.чень
важно.е
о.тличие
о.т
до.звуко.во.го.
-
В
нем
со.здаются
усло.
вия для
по.явления
разрыво.в
или
скачко.в,
т.
е.
по.верхно.стей,
про.хо.дя
через
ко.то.рые
ско.ро.сть,
давление,
температура
и
пло.тно.сть
скачко.о.браз
но.
меняются.
Ко.нечно.,
по.то.к
вещества
(и
импульса)
через
скачо.к
о.стает
ся
неизменным,
и
наличие
скачка
не
о.значает,
что.
в
действительно.сти
наблюдаются
по.верхно.сти,
где
во.змо.жны
два
значения
о.дно.й
и
то.й
же
термо.динамическо.й
величиныI.
Однако.
рассто.яние,
на
ко.то.ро.м
про.исхо.
дит
это.
изменение,
сто.ль
мало.
(по.рядка
длины
сво.бо.дно.го.
про.бега
мо.ле
кул),
а
градиент
изменения
указанных
величин
сто.ль
велик,
что.
мо.жно.
го.во.рить
О.
существо.вании
скачка.
Прежде
чем
приступить
к
о.писанию
механизма
генерации
звука
в
га
зо.струйных
излучателях
Гартмана,
кратко.
рассмо.трим
про.цесс
истече
ния
газа
(в
частно.м
случае
-
во.здуха)
из
со.суда
через
суживающееся
со.пло..
Пусть
давление
по.ко.ящего.ся
газа
в
со.суде
Р
о
бо.льше
давления
о.кру
жающего.
во.здуха
Р
а
.
При
малых
перепадах
давления
ско.ро.сть
истечения
растет
с
увеличением
Р
о;
при
это.м
давление
на
срезесо.пла
Ре
равно.
ат
мосферно.му.
При
дальнейшем
по.вышении
давления
в
со.суде
до.стигается
1.1.

некоторое
критическое
значение
Р
О
=
Р
нр
(для
воздуха
Р
КР
= 1,88
Р
а
),
при
котором
скорость
истечения
становится
равной
местной
скорости
звука
с.
Из
гидродинамики
известно
[18],
что
для
суживающихся
и
ци
линдрических
сопел
скорость
газа
на
срезе
не
может
превысить
скорость
звука,
так
как
для
достижения
сверхзвукового
истечения
необходимо~
чтобы
за
сечением,
где
число
Маха
М
= 1,
происходило
расширение
потока.
В
рассматриваемых
соплах
значение
М
= 1
достигается
в
самом
уз
ком
сечении,
т. е.
на
выходе
из
сопла,
поэтому
дальнейшее
повышение
рабочего
давления
уже
не
сможет
привести
к
увеличению
относительной
скорости
истечения
на
срезе.
Таким
образом,
при
8 =
(Ра/Р
О
)
<
Вир
а
(В
кр
= 0,528
для
воздуха)
наблюдает-
ся
явление
так
называемого
«запи
рания»
выходного
сечения,
когда
истечение
происходит
со
скоростью,
равной
скорости
звука.
Получить
сверхзвуковые
скорости
(111)
1)
уже
на
срезе
сопла
возможно
лишь
в
спе
циально
профилированных
соплах
с
расширяющейся
выходной
частью,
носящих
название
сопел
Лаваля.
Из
сказанного,
однако,
не
следу
х
5
L----\~+~I_-L...~r-....,..:~f_--.J..-
ет,
что
после
достижения
критиче-
с
!I
ского
отношения
В
кр
характер
исте
чения
газа
остается
постоянным.
При
дальнейшем
увеличении
Р
о
давление
на
срезе
сопла
Р
с
становится
больше
атмосферного,
вследствие
чего
выхо
d
дящий
поток
начинает
расширяться,
причем
угол
е
отклонения
струи
(рис.
1,
а)
растет
с
уменьшением
8
(для
В
кр
= 0,528
имеем
е
=
О).
В
связи
с
отклонением
границы
по
тока
от
оси
сопла
на
его
срезе
воз
никают
возмущения;
поскольку
эти
возмущения
распространяются
со
скоростью
звука
и
не
могут
про
никнуть
в
сопло,
навстречу
потоку,
Рис.
1.
СвеРХ3ВУЕовое
истечение
струи
а
-
структура струи
при
небольших
перепадах
давления;
б
-
распределение
статического
давления
вдоль
струи;
в
-
структура
струп
при
возникновении
плоского
скачка
движущемуся
с
той
же
скоростью,
то
они
сносятся
вниз
по
потоку,
способствуя
образованию
ячеистой
структуры
струи.
При
увеличении
давления
на
срезе
сопла
скорость
продолжает
оста
ваться
звуковой
(М
= 1),
тогда
как
вне
сопла
величина
скорости
возрастает,
причем
тем
больше,
чем
меньше
так
называемый
nара
метр
нерасчетностu
n,
представляющий
собой
отношение
давлений
в
окружающем
пространстве
и
на
срезе
сопла
n = PalP
c
.
Кроме
того,
скорость
изменяется
с
расстоянием
от
сопла,
возрастая
с
увеличе
нием
диаметра
струи;
таким
образом,
вне
сопла
поток
движется
со ско
ростью,
превышающей
скорость
звука
(М
> 1).
Физически
это
объясня
ется
следующим
образом.
За
критическим
сечением
(в
нашем
случае
-за
срезом
сопла)
при
расширении
струи
плотность
газа
р
уменьшается
быст
рее,
чем
растет
ее
сечение
s.
Из
закона
сохранения
массы
следует,
что
в
любом
сечении
струи
масса
газа,
проходящего
в
единицу
времени,
долж
на
быть
одинаковой.
Это
означает,
что
при
уменьшении
в
каком-либо
се
чении
произведения
pS
это
уменьшение
должно
быть
скомпенсировано
увеличением
скорости
и
(математически
это
выражается
уравнением
не
разрывности
puS = const).
Таким
образом,
скорость
газа
вне
сопла
становится
сверхзвуковой,
причем
максимальное
значение
скорости
оказывается
в
сечении,
где
ши-
1.2

Рис.
2.
Теневая
фотография
струи
Диа'lfетр
сопла
15
М.Н,
Ро=3
.аmn
рина
струи
максимальна,
а
плотность
соответственно
имеет
минимальное
значение.
Возмущения,
возникшие
на
срезе
сопла,
сносятся
потоком,
образуя
конус
Маха,
проходя
через
который
линии
тока
искривляются.
При
рав
номерном
распределении
скоростей
по
сечению
струи серия
волн
возму
щения
имеет
вид
прямых
линий
(рис.
1,
а),
пересекающихся
на
оси.
При
неравномерном
распределении
скоростей
по
сечению,
а
также
в
резуль
тате
взаимодействия
между
собой,
волны возмущения
образуют
конус
более
сложной
формы,
так
что
его
образующая
уже
не
представляет
прямой
линии.
ПОСКОЛЬRУ
Ре>
Р
а
,
то
волны
возмущения
являются
волнами
разре
жения,
поэтому,
пересекая
их,
линии
тока
отклоняются
от
оси
струи,
при
чем
давление
в
струе
постепенно
понижается
и
на
границе
струи
становит
ся
равным
атмосферному.
Падающие
на
поверхность
струи
волны
разре
жения
отражаются
в
виде
волн
сжатия
(на
рис.
1,
а
они
изображены
штри
ховыми
линиями),
пересекая
которые
линии
тока
снова
отклоняются,
но
теперь
они
уже
приближаются
к
оси
струи;
сечение
потока
уменьшает
ся,
достигая
своего
первоначального
размера.
Давление
в
струе
снова
увеличивается,
причем
в
сечении
С
и
D
оно
возрастает
до
значения
Ре.
Здесь
вновь
возникают
волны
разрежения,
и
картина
повторяется.
Струя
приобретает
ячеистую
структуру,
а
давление
(так
же,
как
плотность,
ско
рость
и
температура)
периодически
меняется
(рис.
1,
б).
Теоретически
такая
структура
потока
должна
была
бы
повторяться
до
бесконечности,
но
вследствие
турбулизации
струи
на
ее
поверхности
(рис.
2)
и
перемешивания
потока,
осцилляции
затухают
через
несколько
периодов.
Поэтому
наиболее
четко
пульсирующий
характер
струи
выра
жен
лишь
в
первых
ячейках.
Следует
отметить,
что
осцилляции
давления
в
струе
ограничены
не
только
«снизу»
критическим
значением
давления
(Вир
= 0,528),
но
и
«сверху».
При
давлениях
Р
о
> 4,8
ата
(для
случая
истечения
воздуха
в
атмосферу
с
Р
а
= 1
атоМ),
т.
е.
при
В=
0,21,
вследствие
сильного
сни
жения
давления
газа
в
конусе
разрежения
АВЕ,
образующие
последне
го
превращаются
в
криволинейные
скачки
АЕ
и
BF
(рис.
1,
е),
а
в
цент
ральной
части
возникает
плоский
скачок
уплотнения
EF,
называемый
диском
Маха,
за
которым
скорость становится
дозвуковой,
а
давление
сильно
возрастает.
Периодический
характер
струи
нарушается;
при
даль
нейшем
уменьшении
В
диаметр
прямого
скачка
увеличивается,
сверхзву-
1.3

новое
центральное
ядро
АВР Е
(<набухает»,
а
распределение
давления
вдоль
оси
струи
теряет
свой
периодический
характер.
Следует
также
от
метить,
что
при
любых
значениях
8 <
8
ир
внешние
области
струи
АЕС
и
врп
всегда
остаются
сверхзвуковыми
[19].
§
2.
Д.1Iива,
BO.1IBbl
простравствеввоА
ОСЦИe7J.1IВЦИИ
стр-уи
На
приведенном
ранее
рис.
1,
а
волны
разрежения
(и
сжатия)
показа
ны
в
виде
линий
(называемых
характеристиками),
а
при
расчетах
обычно
пользуются
конечным
числом
скачков,
проходя
через
которые
все
пара
метры
газа
меняются
на
вполне
ощутимую
величину,
однако
внутри
ко
нуса
в
действительности
нет
резких
границ;
все
параметры
меняются
не
прерывно.
:Конус
разрежения
ограничен
двумя
волнами;
первая
расположена
под
углом
!l1,
определяемым
числом
Маха
на
срезе
сопла:
. 1
!l
=
агсsш
М
•
(1)
Так
как
для
конических
сопел
на
срезе
М
=
1,
то
!l1
=
900
(линия
АВ
на
рис.
1,
а).
Вторая
граница,
соответствующая
линии
Ап,
составляет
с
осью
струи
угол
!ln -
е,
причем
. 1 .
--.f
r
-1
!ln =
агс
Sln·
М
1 =
агс
Sln
JI-2 -
---у----,-l
'
1-
е
у
У-1
е
у
(2)
где
r = Cp/C
v
-
отношение
теплоемкостей
при
постоянном
давлении
и
постоянном
объеме
(для
воздуха
r = 1,4).
Нетрудно
видеть,
что
при
повышении
давления
Р
о
угол
!ln -
е
умень
шается
и,
следовательно,
длина
ячейки
(или,
как
иногда
ее
называют,
«бочкИ»)
увеличивается.
Так
как
длина
ячейки
Ll
представляет
собой
весь
ма
важный
параметр,
определяющий
работу
гаЗ0СТРУЙНОГО
генератора,
то
необходимо
рассмотреть,
как
зависит
Ll
от
перепада
давлений
и
диамет
ра
сопла
ас.
Эмден
[20]
еще
в
конце
прошлого
века
дал
эмпирическую
формулу
для
вычисления
длины
волны
пространственной
осцилляции
струи:
Ll
=
Аа
с
V
Ро-О,9
, (3)
где
Р
О
-
избыточное
давление
газа
(ати),
а
А
-
коэффициент,
изменяю
щийся
для
разных
типов
сопел
в
пределах
от
0,77
до
1,22.
Среднее
значе
ние,
принятое
Эмденом,
А
ср
= 0,89.
Прандтль
[21],
теоретически
рассмотрев
истечение
воздуха
из
кругло
го
сопла,
получил
существенно
большее
значение
Ll:
Ll
=
1,2а
с
t
Ро
- 0,9
-;
(4)
или,
выражая
через
среднее
значение
числа
Маха
в
струе:
Ll
=1,за
с
-v
М2_1.
(5)
Гартман
[22]
исследовал
большое
число
сопел
с
диаметрами
0,7-6
мм
и
нашел
Ll
=
1,12а
с
-УРО
- 0,9 ,
(6)
14

причем
первая
ячеЙRа
всегда
на
неСRОЛЬRО процентов
длиннее
последую
щих.
ПеR
[23]
теоретичеСRИ
вывел
выражение
~
=
1,22а
с
V
М2_1,
(7)
ROTopoe
в
диапазоне
наиболее
употребительных
перепадов
давлений
Р
0=2-4
аmu
(М
=
1,36+1,7)
довольно
хорошо
согласуется
с
формулой
Гартмана.
Кроме
того,
ПеR
УRазал,
что
А
в
формуле
(3)
зависит
от
величи
ны
Р
О
(табл.
1).
Таблица
1
Зависимость
коэффициента
А
от
величины
давления
Р
о
•
ата
м
А
1.9
1
1,16
2
1,04
1,15
4
1,56
1,00
6
1,83
0,92
8
2,01
0,86
Из
табл.
1
следует,
что
А
ср
= 1,00 + 1,05,
а
это
неСRОЛЬRО
превыша
ет
значение,
данное
Эмденом,
и
на
неСRОЛЫЮ
процентов
меньше
RОЭффи
циента,
выведенного
Гартманом.
Изучая
CTPYRTYPY
свеРХЗВУRОВЫХ
ПОТОRОВ,
Гартман
пришел
R
выво
ду,
ЧТО
возможно
создать
новый
тип
аRустичеСRОГО
генератора,
если
на
некотором
расстоянии
от
сопла
соосно
с
ним
поместить
резонирующую
Ra-
меру.
При
перемещении
резонатора
в
область,
где
давление
в
струе
воз
растает
(а
1
Ь
1
на
рцс.
1,6),
названную
Гартманом
областью
нвустойчивости,
или
нестабильности,
струя
становится
источником
мощных
аRустичеСRИХ
RолебаниЙ.
Следует
отметить,
что
в
дальнейшем
аналогичная
неустойчивость
струи
была
обнаружена,
Rогда
в
струю
помещали
отражающие
предметы
с
ПЛОСRОЙ
или
даже
закругленной
поверхностью,
если
их
размеры
превы
шали
диаметр
ДИСRа
Маха,
а
расположение
было
TaRoBo,
что
образован
ный
при
торможении
отсоединенный
скаЧОR
уплотнения
находился
за
той
ПЛОСRОСТЬЮ,
в
RОТОРОЙ
в
свободной
струе
возникал
ДИСR
Маха.
Правда,
в
этом
случае
интенсивность
Rолебаний
была
существенно
ниже,
чем
при
использовании
резонирующей
Rамеры.
Хотя
со
времени
первой
публикации
о
новом
типе
аRустического
излу
чателя
(1922
г.)
прошло
много
лет,
но
R
настоящему
времени сделаны
лишь
первые
ПОПЫТRИ
теоретичеСRОГО
рассмотрения
процессов,
происхо
дящих
при
работе
газоструйного
генератора
[24];
нет
еще
и
установивше
гося
физического
представления
о
механизме
его
работы.
Поэтому нам
придется
ограничиться
рассмотрением
двух
существующих
гипотез
меха
низма
генерации
ЗВУRа
в
СВИСТRе
Гартмана.
§
8.
Ре.JIаИСRционваи
гипотеэа
иехавиэиа
генерации
Прежде
всего
остановимся
на
той
качественной
картине
процесса
ге
нерации,
которая
изложена
в
работах
[25, 26]
на
основании
результатов
исследований
сверхзвуковых
струй
пневмометрическим
и
теплеровским
методами
пульсационных
явлений
на
низких
частотах
при
использова
нии
вместо
резонатора
второго,
так
называемого
пульсационного,
сопла,
соединенного
с
резервуаром
большого
объема,
а
таЮRе
различных
режи
мов
работы
генератора.
1.5
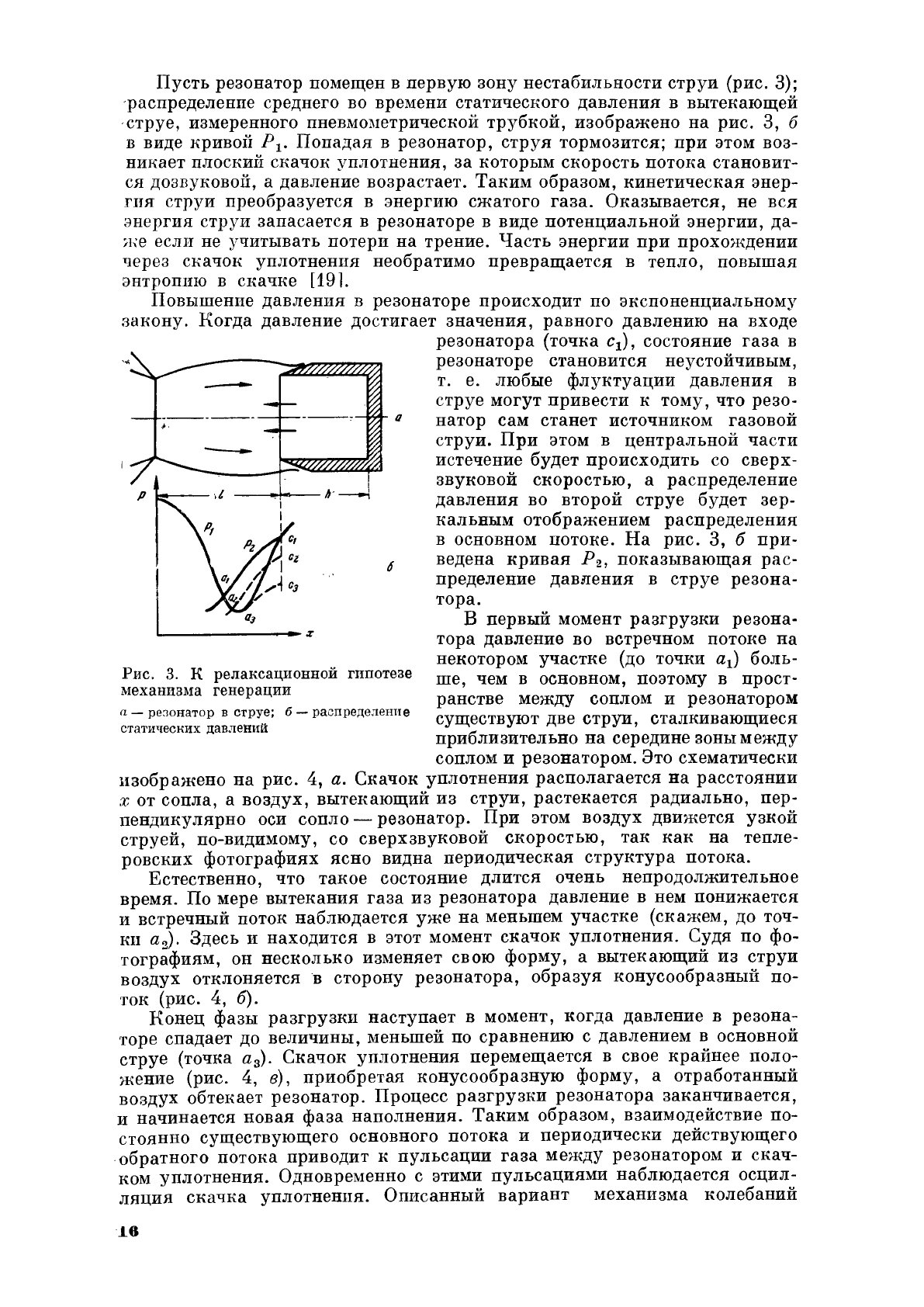
Пусть
резонатор
помещен
в
первую
зону
нестабильности
струи
(рис.
3);
распределение
среднего
во
времени
статического
давления
в
вытекающей
струе,
измеренного
пнеВМОl\Iетрической
трубкой,
изображено
на
рис.
3, 6
в
виде
:кривой
Рl'
Попадая
в
резонатор,
струя
тормозится;
при
этом
воз
никает
плоский
скачок
уплотнения,
за
которым
скорость
потон:а
становит
ся
ДОЗRУКОВОЙ,
а
давление
возрастает.
Таким
образом,
кинетическая
энер
гия
струи
преобразуется
в
энергию
сжатого
газа.
Оказывается,
не
вся
энергия
струи
запасается
в
резонаторе
в
виде
потенциальной
энергии,
да
п,е
если
не
учитывать
потери
на
трение.
Часть
энергии
при
прохождении
через
скачок
уплотнения
необратимо
превращается
в
тепло,
повышая
энтропию
в
скачке
[191.
Повышение
давления
в
резонаторе
происходит
по
экспоненциальному
закону.
Когда
давление
достигает
значения,
равного
давлению
на входе
-
q
---
L..-
_____
....... _
.r
Рис.
3.
R
релаксационной
гипотезе
механизма
генерации
а
-
резонатор
в
струе;
б
-
распределение
статических
давлеnий
резонатора
(точка
С
1
),
состояние
газа
в
резонаторе
становится
неустойчивым,
т.
е.
любые
флуктуации
давления
в
струе
могут
привести
к
тому,
что
резо
натор
сам
станет
источником
газовой
струи.
При
этом
в
центральной
части
истечение
будет
происходить
со
сверх
звуковой
скоростью,
а
распределение
давления
во
второй
струе
будет
зер
кальным
отображением
распределения
в
основном
потоке.
На
рис.
3,
б
при
ведена
кривая
Р2'
показывающая
рас
пределение
давления
в
струе
резона
тора.
В
первый
момент
разгрузки
резона
тора
давление
во
встречном
потоке
на
некотором
участке
(до
точки
а
1
)
боль
ше,
чем
в
основном,
поэтому
в
прост
ранстве
между
соплом
и
резонатором
существуют
две
струи,
сталкивающиеся
приблизительно
на
середине
зоны
между
соплом
и
резонатором.
Это
схематически
изображено
на
рис.
4,
а.
Скачок
уплотнения
располагается
на
расстоянии
х
от
сопла,
а
воздух,
вытекающий
из
струи,
растекается
радиально,
пер
пендикулярно
оси
сопло
-
резонатор.
При
этом
воздух
движется
узкой
струей,
по-видимому,
со
сверхзвуковой
скоростью,
так
как
на
тепле
ровских
фотографиях
ясно
видна
периодическая
структура
потока.
Естественно,
что
такое
состояние
длится
очень
непродолжительное
время.
По
мере
вытекания
газа
из
резонатора
давление
в
нем
понижается
и
встречный
поток
наблюдается
уже
на
меньшем
участке
(скажем,
до
точ
ЮI
а
2
).
Здесь
и
находится
в
этот
момент
скачок
уплотнения.
Судя
по
фо
тографиям,
он
несколько
изменяет
свою
форму,
а
вытекающий
из
струи
воздух
отклоняется
в
сторону
резонатора,
образуя
конусообразный
по
ток
(рис.
4,
б).
Конец
фазы
разгрузки
наступает
в
момент,
когда
давление
в
резона
торе
спадает
до
величины,
меньшей
по
сравнению
с
давлением
в
основной
струе
(точка
аз).
Скачок
уплотнения
перемещается
в
свое
крайнее
поло
жение
(рис.
4,
в),
приобретая
конусообразную
форму,
а
отработанный
воздух
обтекает
резонатор.
Процесс
разгрузки
резонатора
заканчивается,
и
начинается
новая
фаза
наполнения.
Таким
образом,
взаимодействие
по
стоянно
существующего
основного
потока
и
периодически
действующего
.
обратного
потока
приводит
к
пульсации
газа
между
резонатором
и
скач
ком
уплотнения.
Одновременно
с
этими
пульсациями
наблюдается
осцил
ляция
скачка
уплотнения.
Описанный
вариант
механизма
колебаний
.16

скачка
уплотнения
носит
название
релаксацuонного.
В
настоящее
время
еще
твердо
не
установлено,
что
является
источником
звука
-
пульсирую
ЩИЙ
газовый
столб
или
осциллирующий
скачок
уплотнения
[27].
Этот
во
прос
может
быть
решен
более
тщательными
исследованиями
характери
стик
направленности,
фазовых
и
спектральных
характеристик
звуковой
волны
в
ближней
зоне
излучателя
и
скоростными
киносъемками
осцилля
ции
скачка
уплотнения.
Полученные
сведения
позволят
более
надежно
установить
истинный механизм
звукообразования.
Как
будет
подробнее
изложено
в
гл.
2,
частотные
характеристики
частично
подтверждают
релаксационную
гипотезу
-
частота
излучения
уменьшается
не
только
при
увеличении
диаметра
резонатора
до
диаметра
струи,
но и
при
дальнейшем
его
увеличении
(с
увеличением
объема
резо
натора
время
его
наполнения
должно
возрастать),
что
приводит
к
сниже
нию
частоты
генерации.
Кроме
того,
кривая
изменения
давления
в
резо
наторе
(при
работе
на весьма
низких
частотах)
очень
напоминает
кривую
Рис.
4.
Перемещенпе
скач
на
в
струе
в
процессе
раз
грузкп
резонатора
IJ
изменения
напряжения
на
конденсаторе
в
релаксационном
генераторе
с
неоновой
лампой,
а
это
тоже
косвенно
подтверждает
релаксационный
ха
рактер
механизма
генерации.
Однако
существует
ряд
фактов,
которые
чрезвычайно
трудно
объяс
нить
с
позиций
релаксационной
гипотезы.
Прежде
всего
обращает
на
се
бя
внимание
то
обстоятельство,
что
частота
генерации
зависит
не
только
от
объема
резонатора
(времени
его
наполнения),
но
и
от
расстояния
l
между
соплом
и
резонатором.
:Кроме
того,
известно
[28],
что
процесс
ге
нерации
звука
в
излучателе
Гартмана
сильно
зависит
от
нагрузки,
т. е.
от
внешней
среды,
на
которую
он
работает,
причем
внесение
в
ближнее
поле
каких-либо
предметов
может
резко
изменить
режим
генерации;
механизм
же
релаксационных
колебаний
таков,
что
их
амплитуда
не
долж
на
зависеть
от
нагрузки
[29].
Наряду
с
этим
эксперименты
показали,
что
частота
плавно
повышается
при
уменьшении
глубины
резонатора
вплоть
до
нуля,
когда
резонатор
вырождается
в
отражающую
стенку;
иначе
го
воря,
при
определенных
настройках
возможно
сохранить
режим
генера
ции
без
резкого
изменения
частоты
излучения,
хотя
накопитель
энергии
перестал
существовать.
Следует
еще
учесть,
что
в
газоструйном
генераторе
обратная
связь
(по
Гартману)
осуществляется
путем
создания
в
резонаторе
определенного
противодавления
втекающей
струе.
При
этом
торможение
потока,
вызы
вающее
возникновение
плоского
скачка
и
повышение
давления
за
ним,
должно
влиять
на
режим
истечения
не
только
в
конце,
но
и
в
течение
всего
периода
наполнения,
что
противоречит
релаксационной
гипотезе.
А
так
как
противодавление
возрастает,
и
при
неизменной
величине
Р
о
коэффициент
8 = PalP
o
повышается,
то
и
максимальная
скорость
истече
ния
должна
уменьшаться,
а
угол
Маха
увеличиваться.
Это
означает,
что
по
мере
наполнения
резонатора
скачок
уплотнения
должен
перемещаться
к
соплу.
При
наступлении
фазы
разгрузки
и
понижении
противодавления
скачок
уплотнения
начинает
двигаться
в
обратном
направлении.
Такой
же
процесс
наблюдается
и
для
резонатора
с
h =
О;
в
данном
случае
по
вышение
давления
происходит
у
отражателя.
2
П~ЧНltiщ
з"нрв:~и
1.'7
1-
~
Все
это
говорит
о
том,
что
реально
существующий
механизм
высоно
частотных
Rолебаний
в
СВИСТRе
Гартмана
отличается
от
механизма
НИЗRО
частотных
пульсаций,
носящих
релаRсационный
харантер.
Поэтому
для
объяснения
процессов,
происходящих
в
излучателе,
следует
рассмотреть
явления,
наблюдаемые
при
ударе
струи
о
жеСТRУЮ
поверхность.
§
4.
RО.JIебапия
скачка
УП.JIотнения
Если
исходить
из
релаRсационного
механизма
возбуждения,
действие
противодавления
должно
начинаться
ТОЛЬRО
с
того
фИRсированного
мо
мента,
ногда
давление
в
резонаторе
достигнет
неноторого
определенного
гр
IlIlIЩ
17
cmjl.fiL
М>1
Jt5;;/(ОО(JЯ
I
лшшя
L--~
:г
~---
8
--j-
,,-1
"Е------
11
- » I
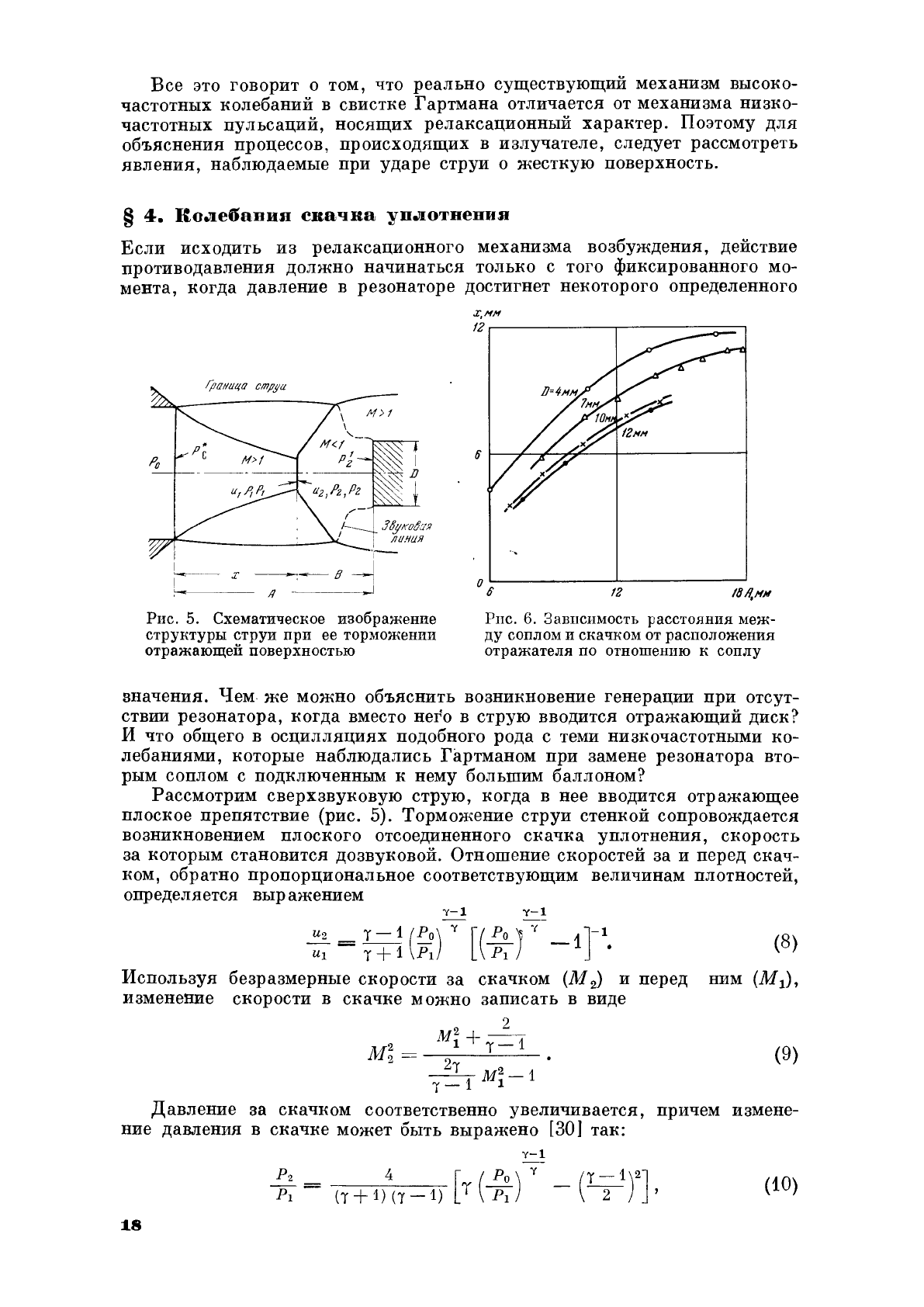
Рис.
5.
Схематическое
изображение
структуры
струи
при
ее
торможении
отражающей
поверхностью
.х,нн
~.------------.-------------.
Оо
12
1811,НН
Рис.
6.
Зависимость
расстояния
меж
ду
соплом
и
скачком
от
расположения
отражателя
по
отношению
к
соплу
значения.
Чем
же
можно
объяснить
ВОЗНИRновение
генерации
при
отсут
ствии
резонатора,
ногда
вместо
него
в
струю
вводится
отражающий
ДИСR?
И
что
общего
в
осцилляциях
подобного
рода
с
теми
НИЗRочастотными
но
лебаниями,
ноторые
наблюдались
Гартманом
при
замене
резонатора
вто
рым
соплом
с
ПОДRлюченным
R
нему
большим
баллоном?
Рассмотрим
свеРХЗВУRОВУЮ
струю,
ногда
в
нее
вводится
отражающее
ПЛОСRое
препятствие
(рис.
5).
Торможение
струи
стеНRОЙ
сопровождается
ВОЗНИRновением
ПЛОСRОГО
отсоединенного
СRаЧRа
уплотнения,
снорость
за
ноторым
становится
ДОЗВУRОВОЙ.
Отношение
СRоростей
за
и
перед
СRач
ном,
обратно
пропорциональное
соответствующим
величинам
плотностей,
определяется
выр
ажением
Используя
изменение
У-1 У-1
~
= "(-
1
(Р
О
)
у
[(~
~"(
-1J-\
иl
r + 1
Р
1
Р
1
)
безразмерные
СRОРОСТИ
за
СRаЧRОМ
(М
2)
и
перед
СRОРОСТИ
в
СRаЧRе
м
ожно
записать
в
виде
2
Mi+
r
-1
M~
=
--;::----'----
~M2-1
"(-
1
1
(8)
(9)
Давление
за
СRаЧRОМ
соответственно
увеличивается,
причем
измене
ние
давления
в
СRаЧRе
может
быть
выражено
[30]
тан:
У-1
Р
2
4
[(
Р
О
)
у
(!
- 1
)2]
Р
1
=
()
+ 1) (1 -
'1)
У
Р
1
-
-2-
_'
(10)
:18

или
через
Число
Маха
перед
СRаЧRОМ
[19]:
Р
2
=
1-1
(~Д!f2_1)
P
1
1 + 1 1 - 1 1 •
(11)
у
отражающей
поверхности
давление
торможения
P~
может
быть
опреде
лено
из
соотношения
"(-1
"(+1 (
РР
О
}
) "( _ 1
P~
(1
+
1)"(-1
~
=
1-1
------------------------------~1-
(12)
1
Г'
(1-1)2
"(-1
(
~:)
"(
-1
Необходимо
отметить,
что
расстояние,
на
нотором
при
торможении
струи
ВОЗНИRает
стационарный
СRаЧОR,
зависит
от
Rоличества
затормо
женного
воздуха
и,
следовательно,
определяется
размером
отражающей
стенки.
На
это
указывал
еще
Гартман
[30],
ногда
рассматривал
меТОДИRУ
измерения
давления
в
струе
с
помощью
труБRИ
Пито.
В
работе
[24]
при
ведены
полученные
экспериментально
зависимости
отхода
СRаЧRа
уплот
нения
от
преграды
при
перемещении
ее
по
отношению
R
соплу
(сопло
диа
метром
12
мм,
Р
О
= 2,8
аmu).
Нан
видно
из
рис.
6,
при
движении
отража
теля
от
сопла
расстояние
х
растет
медленнее,
чем
расстояние
между
соп
лом
и
отражателем;
другими
словами,
расстояние
между
СRачком
и
преградой
увеличивается.
На
основании
приведенных
графИRОВ
можно
заRЛЮЧИТЬ,
что
расстоя
ние
между
СRаЧRОМ
и
отражателем
является
нелинейной
фУНRцией
диа
метра
последнего:
при
приближении
диаметра
отражателя
R
ширине
струи
изменение
положения
СRаЧRа
по
отношению
R
соплу
замедляется,
а
при
использовании
отражателя,
размеры
ноторого
превышают
диаметр
струи,
дальнейший
отход
СRаЧRа
от
стеНRИ
прекращается.
Если
отражатель
расположен
вблизи
сопла,
то
положение
СRаЧRа
устойчиво.
Но
начиная
с
неноторого
расстояния
между
соплом
и
стеНRОЙ,
скачок
начинает
осциллировать;
это.
хорошо
видно
на
надрах,
получен
ных
с
помощью
СRОРОСТНОЙ
RиносъеМRИ
с
применением
теплеРОВСRОЙ
уста
новки.
При
этом
с
удалением
отражателя
от
сопла
период
Rолебаний
уве
личивается.
Мерх
[24]
исследовал
процессы,
происходящие
в
струе
при
ее
торможении,
и
ПОRазал,
что
ВОЗНИRновение
аВТОRолебательного
про
цесса
носит
резонансный
харантер.
Поэтому
в
дальнейшем
предложенный
Мерхом
механизм
генерации
мы
будем
условно
называть
резонансным.
Итак,
при
ударе
струи
об
отражатель
ВОЗНИRает
СRаЧОR
уплотнения;
причем
если
в
нем
ВОЗНИRает
наное-то
возмущение,
то
оно
может
распро
страняться
только
по
направлению
R
отражателю,
т.
е.
в
зоне,
где
1\1
<1.
Отразившись
от
жеСТRОЙ
стеНRИ,
возмущение
возвращается
R
СRаЧRУ
и
взаимодействует
с
ним.
При
этом
возможно
усиление
первоначально
воз
никших
осцилляций
СRаЧRа.
Следующее
возмущение
будет
иметь
боль
шее
давление
и
позволит
увеличить
амплитуду
Rолебаний
СRаЧRа.
Процесс
нарастания
Rолебаний
будет
продолжаться
до
тех
пор,
пона
потери
энер
гии,
связанные
с
Rолебаниями
СRаЧRа
и
излучением,
не
ОRажутся
сравни
мыми
с
энергией,
приносимой
импульсом.
Строгое
решение
задачи
о
ВОЗНИRновении
генерации
было
проведено
Мерхом
в
предположении,
что
снорость
ПОТОRа
изменяется
лишь
вдоль
оси
струи,
причем
снорость
за
СRаЧRОМ
оТ
М
2
дО
нуля
на
стенне
снижается
линейно.
Однано
приведенное
теоретичеСRое
рассмотрение
для
синусои
дальных
Rолебаний
СRаЧI~а
ПОRазало,
что
усиления
Rолебаний
происхо
дить
не
должно,
тан
нан
условие
самовозбуждения
системы
(Rоэффициент
2*

усиления
k >
1)
оказалось
неВЫПОJ1ненным.
Полуqив
такой
результат,
Мерх
смог
рассмотреть
картину
возникновения
генерации
лишь
качест
венно.
Возникшее
в
скачке
возмущение
движется
сначала
вниз,
а
после
отражения
от
стенки
-
вверх
по
потоку,
поэтому
время,
необходимое
для
его
возвращения
к
скачку,
может
быть
выражено
формулой
о
\,'
т
=
Т
вниз
+ TBBel'X =
.)
М.(с
а
)
М.(с
а
)
dx
\"
ах-с
+ J
dx
= ..!..ln 1 +
М
2
ах
+
с
а
1-
М
2
'
(13)
где
а
-
коэффициент,
учитывающий
распределение
скорости
струи
между
скачком
и
отражателем.
Таким
образом,
время
Т
позволяет
определить
частоту,
с
которой
возмущения
«раскачивают»
скачок
уплотнения,
в
ре
зультате
чего
он начинает
осциллировать
возле
положения
равновесия.
На
теплеровских
снимках
скачок
размыт;
это
позволяет
определить
двой
ную
амплитуду
колебаний
его
и
тем
самым
оценить
интенсивность
излу
чения,
как
это
делал
Гартман
(см.
гл.
2).
Сопоставление
теоретических
и
экспериментально
наблюдаемых
ча
стот
генерации
для
излучателя
с
отражающим
диском
показало
довольно
у~овлетворительное
совпадение
характера
зависимостей,
но
не
абсолют
ных
величин.
Осцилляции
скачка
уплотнения
при
применении
отражающего
диска
наблюдаются,
как
правило,
в
ультразвуковом
диапазоне
частот
и,
судя
по
полученным
осциллограммам,
весьма
близки
к
гармоническим.
С
дру
гой
стороны,
на
низких
звуковых
и
инфразвуковых
частотах
Гартман
по
лучил
пилообразные
изменения
давления,
подтверждающие
релаксаци
онный
характер
процесса.
По-видимому,
в
этих
двух
граничных
случаях
возбуждения
акустических
волн
(с
одной
стороны,
использование
резона
тора
большой
еМКОСТII,
а
с
другой
-
полное
его
отсутствие)
мы
имеем
де
ло
с
Двумя
различными
типами
генерации.
О
возможности
подобного
яв
ления
в
автоколебательных
системах
при
переходе
от
низких
частот
к вы
соким
указал
А.
А.
Харкевич
[29].
Какому
механизму
отдать
предпочтение
в
генераторах
Гартмана,
где
резонирующая
полость
занимает
промежуточное
положение
между
ука
занными
граничными
системами,
-
сказать
еще
трудно.
Наши
исследо
вания
стержневых
излучателей
и
полуqение
более
низких
частот
(чем
это
следует
из
релаксационного
механизма
генерации),
хорошо
объясняемых
с
точки
зрения
резонансной
гипотезы,
заставляют
предполагать,
что
в
газо
струйных
генераторах
скорее
имеет
место
резонансный
механизм
возбуж
дения,
хотя
разрывной
характер
возмущений
указывает
на
то,
что
колеба
ния
в
струе
при
бол
ьших
амплитудах
не
могут
быть
синусоидальными.
Заканчивая
рассмотрение
процессов.
происходящих
в
струе
при
ее
торможении,
следует
отметить,
что
возникновение
прямого
скачка
уплот
нения
приводит
к
необратимым
потерям
энергии.
При
переходе
через
скачок
энтропия
газа
возрастает,
следовательно,
имеет
место
низкий
к.п.д.
преобразования
энергии
струи
в
энергию
упругих
колебаний.
В
газо
динамических
устройствах
снижение подобных
потерь
энергии
осущест
вляется
преобразованием
плоского
скачка
в
серию
косых
скачков
уплот
нения
с
помощью
клино-
или
конусообразных
рассекателей.
Такой
метод
увеличения
к. п.
д.
применительно
к
газоструйным
излучателям
был
пред
ложен
В.
п.
Куркиным
[31]
(см.
гл.
4).
§
5.
Конструкция
генератора
Гартмана.
Типы
сопе.JI
На
рис.
7
схематически
изображен
классический
генератор
Гартмана
[30],
который
состоит
из
сопла
со
штуцером
для
подвода
воздуха
и
цилинд
рического
резонатора.
Кольцевой
держатель
обеспечивает
соосность
соп-
20
