Roy K.K. Potential theory in applied geophysics

Подождите немного. Документ загружается.

15.2 Finite Diﬀerence Formulation/Direct Current Domain 479

Therefore, for the point i, j + h

,wecanwrite



dφ



i,j+

− φ

i,j−

+ h

) /2

. (15.10)

Hence



∂φ

∂x



i,j+hE/2



i,j+hE/2



−1

(φ

i,j+hE

− φ

i,j

) . (15.11)

Now



∂

∂x



∂φ

∂x



will be from (15.9)



∂

∂x



∂φ

∂x



i,j

+ h

)



∂φ

∂x



i,j+hE/2

−



∂φ

∂x



i,j−hW/2

. (15.12)

Putting the values from (15.10), we get



∂

∂x



∂φ

∂x



i,j

+ h



i,j+hE/2



i,j+hE

− φ

i,j



−

i,j−hw/2



i,j

− φ

i,j−hw



(15.13)

Hence (15.6) can be written as

∂

∂x



∂φ

∂x



i,j

∂

∂z



∂φ

∂z



i,j

+ q (x, z)=0

⇒

+ h



i,j+hE/2

(φ

i,j+hE

− φ

i,j

) −

i,j−hw/2

(φ

i,j

− φ

i,j−hw

)

+ h



i,j+hS/2

(φ

i,j+hS

− φ

i,j

) −

i,j−hN/2



i,j

− φ

i,j−hN/2,j



+ q

ii,j

=0. (15.14)

We can rewrite this equation separating the terms of ϕ as,

i,j+hE

+ α

i,j−hW

+ α

i−hN,j

+ α

i+hS,j

−α

+ q

= 0 (15.15)

where



i,j+hE/2



+ h

)]

−1



i,j+hW/2



+ h

)]

−1



i,j+hN/2



+ h

)]

−1

(15.16)



i,j+hS/2



+ h

)]

−1

= α

+ α

Upto this point, we have calculated the values inside the medium.

If we consider the ground surface element, the equation changes in the

following way. Here we consider a ﬁctitious row of elements above the surface

480 15 Numerical Methods in Potential Theory

of the ground such that

= h

and σ

1−hN,j

= σ

1+hS,j

as i = 1 represent the g round surface j = 1, 2,

3 ...... .................n. Hence

= α

(15.17)

for the element (1, j). We must have

∂φ

∂z

= 0 [boundary condition]. This is

only possible if

1+hS,j

= φ

1−hN,j

. (15.18)

Putting (15.15) and (15.17) in (15.14) are have

i,j+hE

+ α

i,j−hW

+ α

i−hS,j

+ α

i,j

+ q

=0. (15.19)

From the entire set of equations obtained for both the surface and subsurface

nodes, one gets a matrix equation of the form AΦ = B (Fig. 15.5)

AΦ= B (15.20)

Since potential is computed in a two dimensional xz plane, the source and the

sink extend to inﬁnite distance along the y directio n . Therefore these sources

are line sources. For converting these potential due to a line source and sink

to potentials due to a point source and sink, integral transform must be used.

15.2.5 Inverse Fourier Cosine Transform

For two-dimensional earth models, the potentials computed are for line source

when it remains independent of one co-ordinate axis. The resistivity distribu -

tion is assumed to be a function of only two co-ordinates (x, z). Since three

dimensional point source is used, the problem cannot be treated purely as

three-dimensional. It is necessary to remove the source variation along y direc-

tion by fourier transformation in order to solve the two-dimensional problem.

Assuming symmetry along y = 0, the potential variations may be transformed

by the application of inverse fourier cosine transformation. We deﬁne

φ (x, y, z)=

∞



φ (x, λ, z) Cos(λy)dλ (15.21)

A Φ = B

Fig. 15.5. Curtoon of a system matrix in ﬁnite diﬀerence problem using Poisson’s

equation and showing sparsity

15.2 Finite Diﬀerence Formulation/Direct Current Domain 481

On the y-axis or when y = 0, we get

ϕ (x, o, z)=

∞



φ (x, λ, z)dλ (15.22)

where λ is the integration variable. Many authors (Mwenifumb o (1980), Sasaki

(1982 ), Dey and Morrison (1976), Pridmore (1978)) have used 5 to 7 values of

integration variables λ between 0 and some ﬁnite value to bring down the upper

limit of integration form ∞. Behaviour of this integr al is studied in greater detail.

It was found that better results are obtained if the λshave a gaussian distribu-

tion between the limits of integral. Therefore the principle of gauss quadrature

integration is followed for evaluating (15.21). Using this pro cedure the eﬀect of

diﬀerent sets of λ valu es on the accuracy in computing potentials with distance

from the source in the working area is examined in detail.

It is observed that, within ﬁxed limits of integration, higher the number

of λ values, greater will be the distance of the point from the source till the

analytical and computed values of p o tential have a considerable agreement.

For example, the distance will be 50 units, 8 units and 2.5 units for sets with

11, 7 and 3 λ values respectively.

15.2.6 Calibration

The discrepancy between numerical and analytical solutions must be min-

imised comparing the responses fo r the bodies of simpler ge ometries. At this

stage the program source code will be ready for op eration.

Figure 15.6 shows a two electro de apparent resistivity proﬁle over a vertical

dyke of higher re sistivity obtained using ﬁnite diﬀerence source code. Values

are compared with those obtained using analytical formulae based on image

theory (see Chap. 11).

Fig. 15.6. Resistivity two electrode proﬁle across a vertical dyke; comparision

b etween the ﬁnite diﬀerence model and that obtained with those obtained from

analytical solution

482 15 Numerical Methods in Potential Theory

15.3 Finite Diﬀerence Formulation Domain

with Cylindrical Symmetry DC Field Borehole

Geophysics

15.3.1 Introduction

In this section ﬁnite diﬀerence modelling in DC ﬁeld for a domain of cylindri-

cally symmetric structure is given h ighlighting some diﬀerence in the bound-

ary conditions, geometry of the model and grid system used. In this model

the domain extends from r = 0 to r = ∞ and z = ±∞ whereristheradial

distance from the axis of the cylinder and z is the vertical distance of both

upward and downward boun d aries. Discretization of one half of the r-z plane

for solution of the boundary value problem is only needed. That reduces the

computer storage space considerably. In this section a few more points on

ﬁnite diﬀerence modelling are discussed. Figure (15.7) shows the geometry of

a problem in a zone of cylindrical symmetry. In this problem the Neumann

boundary condition is satisﬁed on the axis of a cylindrical domaim. Dirichlet

boundary conditions will be met at r = ∞ and z = ± ∞. The model is set

up in a c ylin drical co-ordinate system. A point source, located in a radially

symmetric environment, generate the potential ﬁeld.

The proposed medium, with certain structures, is discretized and divided

into rectangular blocks by using vertical and horizontal grid lin es, whose

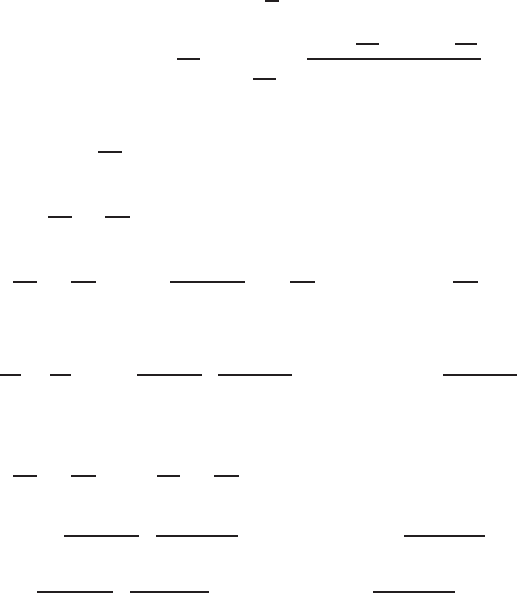
Fig. 15.7. Borehole model with coaxial cylindrical symmetry; coaxial cylindrical

zones respectively show the borehole mud, ﬂushed zone, invaded zone, uncontami-

nated zone and shoulder beds on top and bottom (Anon 1972)

15.3 Finite Diﬀerence Formulation Domain with Cylindrical Symmetry 483

mutual separations increased exponentially, b oth in the vertical and r adial

directions. Radial variation of resistivity in one of the coaxial cylindrical shells

is simulated in FD modelling.

15.3.2 Formulation of the Problem

In a cylindrical co-ordinate system with radial symmetry, the starting Pois-

son’sequationiswrittenas

∂

∂r



∂ϕ

∂r



∂

∂z



∂ϕ

∂z





∂ϕ

∂r



+ q = 0 (15.23)

where, σ = σ (r, z) and ϕ = ϕ (r, z). This relation represents an elliptic second

order diﬀerential equation and deﬁnes the electric potential due to a current

source in a medium. The quantity q must be interpreted as a variable current

density in a typical 3-dimensional model, which is reduced to 2-dimension in

the cross section considering rad ial symmetry.

15.3.3 Boundary Conditions

For ﬁnite diﬀerence modeling, the inﬁnite medium is made ﬁnite by placing

an artiﬁcial boundary. Figure (15.7) shows one such boundary in vertical

cross section of an earth model. The medium is discretized by dividing it into

number of rectangular cells with vertical and radial grids. The intersection

points of the grid are called pivotal or nodal points.

Pivotal points which lie on the axis of symmetry or the borehole axis

i.e., the boundary through the points P

(1,1)

and P

(

max

′

should follow the

boundary conditions i.e.,

∂ϕ(r, z)

∂r

r=0

= 0 (15.24)

2) and ϕ(r, z) = 0 when r →∞and z →±∞

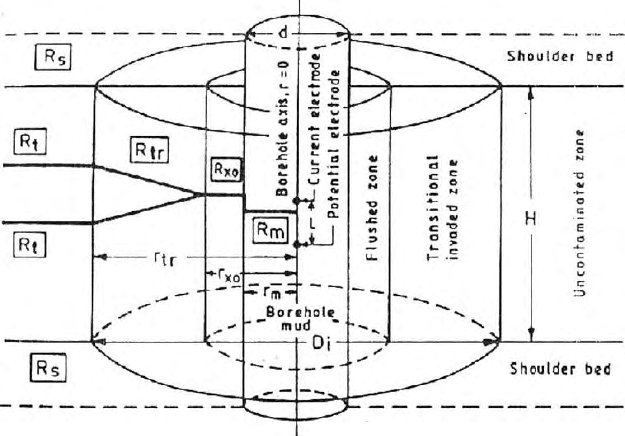
15.3.4 Grid Generation for Discretization

The domain has been discretized using vertical and radial grids. As the model

is axially symmetric, only one half of the vertical section, i.e., r ≥ 0iscon-

sidered. It is necessary that the grids to b e ﬁnely spaced near the current

source (s) as the variation of potential around the source is maximum. As one

moves away from the current source in any direction, the change in poten-

tial gradually diminishes. Hence at points far from the current source, the

grids may be much coarser. It is convenient and justiﬁed to increase the grid

spacing exp onentially with distance from the current source. Co-ordinate o f

a node can be conveniently denoted by (i, j). The node, corresponds to ith

row and jth column can be denoted by P

(i,j)

. j = 1 corresponds to borehole

axis , r = 0, i=i

max

correspond s to the upper and lower boundaries in the

484 15 Numerical Methods in Potential Theory

Fig. 15.8. Expanding grid for ﬁnite diﬀerence modelling; P

1,1

,the location of source

point

vertical plane and j = j

max

corresponds to the radial boundary. The current

point source is lo cated at a point P

(1,1)

(Fig. 15.8).

Location of any pivotal point P

(i,j)

canbeexpressedinanexpandinggrid

system as (Mufti 1976)

r(i, j) =

∆r



j−1

− 1



a −1

for j = 1 to j

max

z(i, j) =

∆z



i−1

− 1



b −1

for i = 1 to i

max

(15.25)

where, a and b are the expansion ratios and ∆r a nd ∆z are the smallest spacing

in the radial and vertical directions respectively. The choice of grid expansion

can be determined by trial and error on the basis o f desired accuracy and

computational eﬃciency.

15.3.5 Finite Diﬀerence Equations

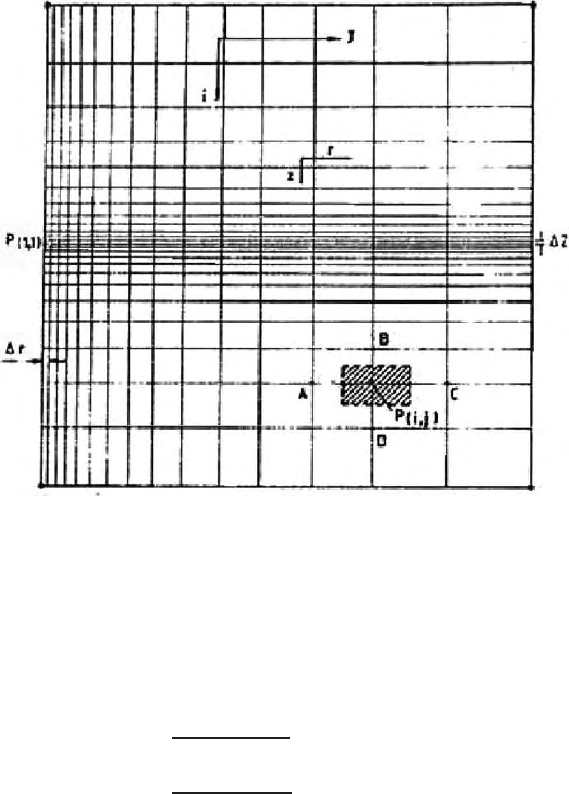
We can consider arbitrarily chosen element P

(i,j)

from the grid system shown

in Fig. (15.9). It’s four immediate surrounding neighbourhood pivotal points

areA,B,CandDdenotedbyP

(i,j−1)

′

(i−1,j)

′

(i,j+1)

and P

(i+1,j)

respectively.

15.3 Finite Diﬀerence Formulation Domain with Cylindrical Symmetry 485

Fig. 15.9. Enlarged view of a rectangular cell in a ring element

Distance from P

(i,j)

to these neighbours can be denoted as h

′

(i,1)

points fall on the borehole axis and are used as locations for current

and potential electrodes on the basis of the required position of which P

(1,1)

is the position of the current electrode. Figure 15.9 is a vertical section of a

three dimensional model. It only represents a slice of the earth and must be

rotated through 360 degrees to represent the actual setup. The 3-dimensional

space is divided into circular ring elements, which have rectangular cross sec-

tions. Figure 15.9 shows a ring disc volume element associated to the nodal

point P

i,j.

. Because of axial symmetry, these r in g elements can be viewed as

rectangular element in the section plane, which reduces the model to 2-D.

Figure (15.9) shows a node P

(i,j)

along with it’s four neighbours. The radial

distance of P

(i,j)

from the b orehole axis (r = 0) is r. Point P

(i,j)

represents the

rectangular element EFGH, covering an area of (h

)/2 ×(h

)/2in

the vertical section. ϕ

i,j

at the point P

(i,j)

in terms of its neighbouring nodal

points can be derived. On account of the central diﬀerence formula, the fol-

lowing approximations are valid at the point P. The diﬀerence equation can

be written as



∂ϕ

∂r



i,j

i,j+h

− ϕ

i,j−h

+ h

. (15.26)

Therefore, for the point (i, j+h

/2), it can be expressed as



∂ϕ

∂r



i,j+h

− ϕ

i,j

. (15.27)

Hence,



∂ϕ

∂r



i,j+h

(ϕ

i,j+h

− ϕ

i,j

) . (15.28)

Similarly for the p oint (i, j −h

/2), one gets,

486 15 Numerical Methods in Potential Theory



∂ϕ

∂r



i,j−h

(σ

i,j

− ϕ

i,j−h

) . (15.29)

Here, σ

i,j+h

and σ

i,j−h

can be expressed as

i,j+h

i,j

+ σ

i,j+h

(15.30)

and

i,j−h

i,j

+ σ

i,j−h

(15.31)

where, σ

i,j

′

i,j+h

and σ

i,j−h

are the conductivity values assumed at the

pivotal points P

(i,j)

′

(i,j+h

)

or P

(i,j+1)

′

and P

(i,j−h

)

or P

(i,j−1)

. Other values

of σ associated with the subsequent equations can be calculated in the same

way. For discr etization of the earth model, conductivity value is assigned to

each element or cell. Since conductivity and resistivity have reciprocal relation

(σ =1/ρ), therefore, the assigned value at the nodal resistivities can be

changed to nodal co nd uctivi ties.

Applying central diﬀerence formula once, one gets



∂

∂r



∂ϕ

∂r



i,j

+ h

)



∂ϕ

∂r



i,j+h

−



∂ϕ

∂r



i,j−h

. (15.32)

Considering (15.28) to (15.31), (15.32) can be expressed as



∂

∂r



∂ϕ

∂r



i,j

+ h



i,j+h

(ϕ

i,j+h

− ϕ

i,j

)

−

i,j−h

(ϕ

i,j

− ϕ

i,j−h

)

. (15.33)

Proceeding in the same fashion, generalized self adjoint ﬁnite diﬀerence

approximation of the diﬀerential equation (15.33) can be represented as

+ h



i,j+h

(ϕ

i,j+h

− ϕ

i,j

) −

i,j−h

(ϕ

i,j

− ϕ

i,j−h

)

+ h



i+h

/2,j



i+h

′

− ϕ

i,j



−

i,j−h

/2,j



i,j

− ϕ

i,h

′



i,j

+ h

)

[ϕ

i,j+h

− ϕ

i,j−h

]+q

i,j

= 0 (15.34)

where, ϕ

i,j−h

′

i−h

′

i,j+h

andϕ

i+h

′

are the potential function associ-

ated to the P

i,j−1

′

i−1,j

′

i,j+1

and P

i+1,j

nodal points.

From (15.34) after separating out the co-eﬃcient of φ,onegets

−α

i,j+h

− α

i,j−h

− α

i+h

′

− α

i,h

′

+ α

i,j

= q

(15.35)

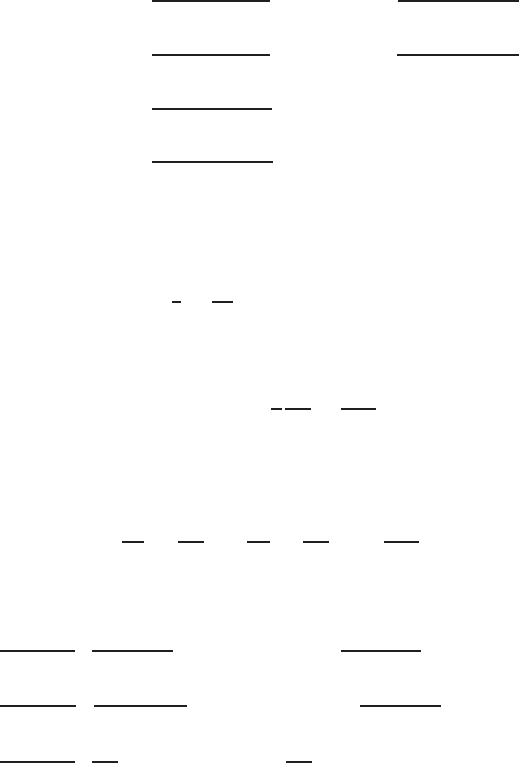
15.3 Finite Diﬀerence Formulation Domain with Cylindrical Symmetry 487

where,

+ h

) h

i,j+h

(

i,j

+ h

) r

i,j

+ h

) h

i,j−h

(

−

i,j

+ h

) r

i,j

+ h

) h

i−h

/2,j

(

(15.36)

+ h

) h

i−h

/2,j

(

= α

+ α

Above (15.35) gives the potential relation for an arbitrary inside pivotal point

i,j

in the discretized domain.

In (15.23) the term



∂ϕ

∂r



, contains a division by r. That leads to mathe-

matical indeterminacy as r → 0 on the borehole axis. This algebraic singularity

is avoided assuming [Mufti (1978, 1980)].

lim

→ 0

∂ϕ

∂r

∂

∂r



r=0

(15.37)

From the (15.23), the generalized expression for evaluating the potential

along the axis of symmetry changes to

∂

∂r



∂ϕ

∂r



∂

∂z



∂ϕ

∂z



+ σ

∂

∂r

+ q =0. (15.38)

Finite diﬀerence equivalent of the (15.38) can be written as

+ h



i,j+h

(ϕ

i,j+h

− ϕ

i,j

) −

i,j−h

(ϕ

i,j

− ϕ

i,j−h

)

+ h



i,j+h

/2,j



i+h

′

− ϕ

i,j



−

i−h

/2,j



i,j

− ϕ

i−h

′



2σ

i,j

+ h



(ϕ

i,j+h

− ϕ

i,j

) −

(ϕ

i,j

− ϕ

i,j−h

)

+ q

i,j

=0. (15.39)

The nodal points, lo cated on the borehole axis, have the value r = 0, and

corresponds to the ﬁrst column of nodes i.e., for j = 1. Hence the co-ordinates

of the pivotal points will be P

(i,1)

. For calculation of p otential on the axis of

symmetry, a ﬁctitious column of element parallel to the axis of symmetry at

the left of (i, 1) is considered and intro duced, such that

(15.40)

and

i,1+h

= σ

i,1−h

. (15.41)

488 15 Numerical Methods in Potential Theory

Elements fall on this axis (i, 1) should satisfy the Neumann boundary condi-

tion

∂ϕ

∂r



r=0

and this is possible only if

i,1+h

= ϕ

i,1−h

. (15.42)

Putting all these assumptions described above in (15.39) and separating out

the coeﬃcient of ϕ,onegets

− α

i,1+h

− α

i+h

′

− α

i−h

′

+ α

i,1

= q

i,1

(15.43)

i,1+h

+2σ

i,j

(

+ h

) h

i−h

/2,1

(

(15.44)

+ h

) h

i+h

/2,1

(

= α

+ α

Equations (15.34) to (15.43) are the main ﬁnite diﬀerence approximations,

which can be solved for the potential expression ϕ (r, z). In practical problems,

a linear equation should be formed using the relations mentioned. Potential

at each node must be expressed in terms of its immediate neighbour and set

of coeﬃcients α

′

, α

′

, α

′

, α

and α

are evaluated. Systematic ordering

of the grid points develops a sparse conductivity coeﬃcient matrix, which is

solved for evaluation of potential ﬁeld at a desir ed location using a suitable

matrix solver.

15.3.6 Current Density Factor q at the Source

In this two dimensional borehole d.c. resistivity forward problem involving

radial symmetry, the source is assumed to be a p oint source and located

along the axis of symmetry which coincides with the borehole axis. It is also

stated that in the expanding grid system the source is considered at the po int

(1,1)

from where the grid expands exponentially on both the sides in the

vertical (z) and radial (r) directions. The volume associated with the piv-

otal point is a cylinder of radius h

/2 and height (h

)/2. Figure 15.10

shows such a volume element a ssociated to any of pivotal points that lie

on the axis of symmetry. The volume of this cylinder can be written as









. Borehole axis is a boundary and Neumann boundary con-

dition is satisﬁed here. The approximation is made considering a ﬁctitious

grid parallel to this axis of symmetry which has already been stated in the

previous section. Let a current of constant strength I be emitted from the