Roy K.K. Potential theory in applied geophysics
Подождите немного. Документ загружается.


14.16 Dyadics 469
∇×
∇×
−→
G
(x)
o
(r, r
o
)+γ
2
−→
G
(x)
o
(r, r
o
)=δ(r, r
o
)x (14.126)
∇×
∇×
−→
G
(y)
o
(r, r
o
)+γ
2
−→
G
(y)
o
(r, r
o
)=δ(r, r
o
)y (14.127)
∇×
∇×
−→
G
(z)
o
(r, r
o
)+γ
2
−→
G
(z)
o
(r, r
o
)=δ(r, r
o
)z (14.128)
The solutions of these equations are
−→
G
(x)
o
(r, r
o
)=
−→
I −
1
γ
2
∇∇
G
o
(r, r
o
)x (14.129)
−→
G
(y)
o
(r, r
o
)=
−→
I −
1
γ
2
∇∇
G
o
(r, r
o
)y (14.130)
−→
G
(z)
o
(r, r
o
)=
−→
I −
1
γ
2
∇∇
G
o
(r, r
o
)z (14.131)
Van Bladel (1968), Tai (1971) Hohmonn (1971, 1975).
Dyadic free space Green’s functions includes all the three components as
−→
G
o
(r, r
o
)=G
(x)
o
(r, r
o
)x+G
(y)
o
(r, r
o
)y+G
(z)
o
(r, r
o
)z (14.132)
and G
o
(r, r
o
) is the nondyadic Green’s function.

15
Numerical Methods in Potential Theory
In this chapter, application of numerical methods in solution of boundary
value potential or field problems in geophysics are discussed. Finite element,
finite difference and Integral equation methods for solution of mostly two and
three dimensional boundary value problems are discussed.
A few geoelectrical problems are presented where these numerical approa-
ches are used. Two dimensional finite difference modelling in direct current
flow field domain both for surface and borehole geophysics (problems with
cylindrical symmetry) are demonstrated in considerable details. Some of the
essential differences in these two problems with difference in geometry are
highlighted. A structure of the low frequency plane wave electromagnetic finite
difference three dimensional modelling (magnetotellurics) is pr e sented briefly.
Two dimensional finite element modelling in direct current flow field in surface
geophysics using Rayleigh Ritz energy minimisation method are discussed in
detail. A brief mention is made about the nature of a 3D problem. Two dimen-
sional fi ni te element modelling in magnetotellurics using Galerkins method is
given. Procedure for using advanced level nodes using isoparametric elements
and Galerkin’s method is outlined. Integral equation method for solution of a
three dimensional electromagnetic boundary value probl em is demonstrated
for low frequency electromagnetics.
15.1 Introducti on
For interpretation of geophysical data, forward problems must be solved before
entering into an inverse problem. Forward problems are mathematically man-
ageable only for models of simpler geometries viz. (i) one dimensional layered
earth problems, (ii) a s p here or a cylinder in a ho mogeneous and isotropic
half space or full space, and (iii) problems with anisotropic half space or
problems where physical property vary continuously with distance. Some two
dimensional problems with simpler geometries are solved analytically. Since
472 15 Numerical Methods in Potential Theory
the subsurface of the earth has a complex geometry, solution of any real-
istic inverse problem demands solution of the forward problems for similar
type of subsurface structure. Thus numerical metho d s entered in p otential
theory with all its well known tools, viz, finite difference, finite element, inte-
gral equation, volume integral, boundary integral, hybrids (mixture) and thin
sheet methods.
With rapid advancement in computation facilities, software technology,
numerical methods in applied mathematics , solvability of geophysical for-
ward problems has increased immensely. Because one ca n insert any amount
of complications in the models and still get a solution. That has revolutionised
the interpretation of geophysical data. The only note of caution is one must
use these tools and softwares only af t er proper calibration. Analytical solu -
tion of a forward problem for a subsurface map of simpler geometries and
its numerical so lu tions must match with mini mum allowable discrepancies.
Because numerical methods are approximate methods always. Application of
these approaches for solving geophysical problems became possible and are
being used extensively these days for two and three dimensional geophysi-
cal problems. Finite difference, finite element and integral equation methods
are well-established subjects because the contributions came from different
branches of physical sciences and technologies.
Foundation of finite element method (FEM ) was laid down by Zienkiewicz,
O.C. (1971), Zienkiewicz and Taylor (1989), Bathe (1977), Kardestuncer
(1987), Reddy (1993), Krishnamurthy (1991). FEM was intro duced in the
electrical methods in geophysics by Coggon (1971), Silvester and Haslam
(1972), Reddy et al (1977), Kisak and Silvester (1975), Ro di (1976), Kaikkonen
(1977, 1986), Pridmore (1978), Pridmore et al (1981), Queralt et al (1991),
Wannamaker et al (1987), Xu and Zhao (1987) and others.
Finite difference modelling in geoelectrical problems became a developed
subject with the contributions from Jepson (1969). Yee (1966), Jones and
Price (1969, 1970), Jones and Pascoe (1972), Stoyer and Greenfield (1976),
Mufti (1976, 1978, 1980), Brewitt, Taylor and Weaver (1978), Dey and
Morrison (1979), Zhdanov and Keller (1994), Mundry (1984), Madden and
Mackie (1989), Mackie et al (1993) , Roy and Dutta (1994) and others.
Integral equation method (IEM) develop ed in geophysics through the con-
tributions from Hohmann (1971, 1975, 1983, 1988), Weidelt (1975), Raiche
(1975), Ting and Hohmann (1981), Stodt et al (1981), Wannamaker et al
(1984), Wannamaker (1991), Beasley and Ward (1986), Eloranta (1984, 1986,
1988), Escola (1992) and others.
Thin sheet modelling grew as a topic in mathematical mo delling with the
contributions from Lajoie and West (1976), Vassuer and Weidelt (1977), Green
and Weaver (1978), Dawson and Weaver (1975), Hanneson and West (1984),
Ranganayaki and Madden (1981).
Hybrid technique developed through the research of Lee et al, (1991), Best
et al (1985), Tarlowskii et al (1984), Gupta et al (1984) and others.
15.2 Finite Difference Formulation/Direct Current Domain 473
Finite difference (FDM) and finite element (FEM) methods are based on
differential equations. Depending upon the subject area the starting equa-
tions are chosen. As for example for geoelectrical and electromagnetic bound-
ary value problems Poisson’s and Helmho l t z electromagnetic wave equations
are the starting points. Every branch of science and engineering where these
mathematical tools are used has their own starting equations. Integral equa-
tion method (IEM),as the name suggests, is based on integral equation and
has great success in handling three dimensional problems in geophysics. In all
the three important numerical methods, the domains are discretized and ulti-
mately the solution of the problem depends upon the efficiency of the matrix
solver. In FDM and FEM, the entire domains are taken into consideration for
solution of the boundary value problems. Therefore size of a matrix becomes
very large for three dimensional problems and they are symmetric or asym-
metric sparse matrics with most of the elements being zeros. In IEM only the
anomalous zones are taken into consideration. Therefore the size of the matrix
is considerably small but solid. That gave upper hand to IEM in handling 3D
problems. But FDM and FEM have better complication handling capability
than IEM.
Mathematical modelling is one of the important areas of geophysics
because it has direct link with understanding the nature of geophysical
data. That will lead to imaging interior of the earth. The steps involved in
mathematical modeling are (i) choice of the basic mathematical equation (ii)
discretization of the domain and mathematical formulation (iii) impostion of
the boundary conditions (iv) Computation of the response on the simulated
air ea rth boundary or inside the earth using a matrix solver. (v) Compari-
son of the model responses obtained by these numerical methods with those
obtained using analytical method for models with simpler geometries; (vi)
refining the numerical tool till the discrepancy between the numerical and ana-
lytical results are minimum (vii) testing the numerical tool, thus developed,
several times with many simpler models for proper calibration and subsequent
use in mathematical modelling.
In this chapter, finite difference, finite element and integral equation meth-
ods are demonstrated for solving direct current resistivity and magnetotelluric
(plane wave electromagnetic) problems in considerable deta ils. These subjects
are well developed. The students have to read all the books and research
papers cited here.
15.2 Finite Difference Formulation/Direct Current
Domain (Surface Geophysics)
15.2.1 Introduction
In finite difference method the first step is to choose the basic equation depend-
ing upon the problem to be solved. As for example we start with Poisson’s

474 15 Numerical Methods in Potential Theory
equation in direct current flow field. Similarly different branches of science
and engineering have their own starting equations. In this finite difference
geoelectrical problem the next step is to change the differential equation to
a difference equation. Since it is an approximation, the very basis on which
the numerical method stands, an attempt is being made to minimise the error
accumulated in this approximation as much as possible. In direct current flow
field the boundary conditions needed and app l i ed are (i) Dirichlet boundary
condition (ii) Neumann boundary condition and (iii) Mixed boundary condi-
tion. Most of the geophysical problems are mixed boundary value pro b lems
where Dirichlet conditions a re satisfied on some boundaries and Neumann
conditions are satisfied on the other.
For a two dimensional direct current flow field problem xz plane is assumed
to be a half space where the domain goes to infinity both in the x(= ±∞)and
z(= +∞), positive downward, directions(Fig. 15.1). For a two dimensional
problem, the physical property along the y direction remains invariant. So
any xz plane will have identical textur e from physical property point of view.
On the surface of the earth or air earth boundary z = 0. Since the upper half
space, filled with air, is an infinitely high resistive zone ,air earth boundary
becomes a boundary of infinite resistivity contrast and Neumann boundary
condition is satisfied at this boundary.
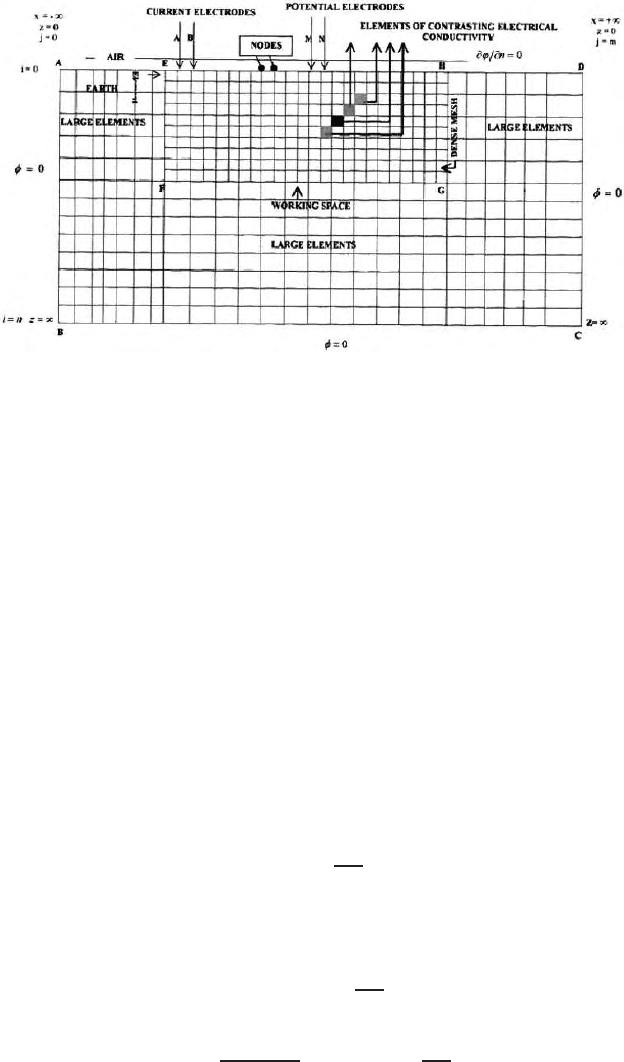
The whole 2D domain is discretized into number of cells or elements
(Fig. 15.1) of generally rectangular or square shapes in finite difference
domain. The intersection points of the grid lines are called nodes (F igs. 15.1
and 15.2). Finite difference equations are generated for each nodes to develop
a matrix equa tion The discreti zed half space is generally divided into two
parts viz, the working zone and the far zone. In the working area the geolog-
ical models are simulated. Dense mesh or grids of much smaller dimensions
are chosen so that in each cell the assumed linear or nonlinear variation of
potential is not a severe approximation. In DC flow field domain, variation of
potential follow 1/r law, which is depicted in s everal connecting elements or
cells. In general the law is higher the p otential gradient smaller should be the
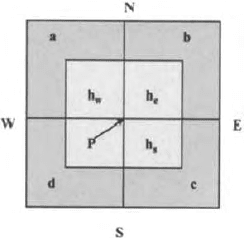
Fig. 15.1. A simplest discretized domain showing the cells, no des and boundaries
15.2 Finite Difference Formulation/Direct Current Domain 475
Fig. 15.2. Enlarged view of a finite difference cell with a node at the centre
grid size and finer should be the mesh. As one moves away from the source,
gradient of potential diminishes, mesh can also be coarser. The general rule is
finer the mesh more accurate will be the finite difference solution, larger will
be the matrix size, higher will be memory allocation in a computer, higher
will be the computation time and more accurately the differential equation is
changed to a difference equation. Depending upon the computational infras-
tructure available one has to make a suitable compromise on the degree of
refinement of the mesh. With the refinement in matrix, the size of the matrix
increases at an alarming rate. To reduce a matrix size often blocks are made
of 4 or 9 or 16 cells having same physical property. For surface of compli-
cated geometry it is advisable to have finer mesh keeping in mind the limited
resolving power of the geoelectrical potentials in mapping the subsurface.
Some grid lines must pass through the assumed geological target such that
it’s effect enters into the mathematical solution. The topic of expanding grid
is discussed in the Sect. 15.3. In the far zone or non working zone the finite
difference cells are made coarser and coarser to make an expanding grid such
that the domain boundaries are pushed back to infinite distances from the
source such that potentials at those b oundaries become zero and Dirichlet’s
boundary condition is sa ti sfied in all the three boundaries (Fig. 15.3). These
boundary conditions will enter into the system matrix modifying some of the
boundary equations.
Difference equations are assembled to generate a matrix equation of large
size. These matrices are sparse matrices with nonzero main diagonal and four
nonzero side diagonals with two nonzero diagonals each in upper and lower
triangle in the matrix. For a 3D problem, the numb er of nonzero side diagonals
will be 3 each in upper and lower tr iangles. Therefore one generally gets penta
diagonal and hepta diagonal matrices for 2D and 3D problems respectively.
Sparsity in a matrix is a guiding equation dependent subject and cannot be
generalised in a few words. But sparsity remarkably reduces computer storage
and computation time because most of the elements are zeros. This matrix
equation is solved using one of the well known and widely used matrix solvers,
viz., Gauss elimination, Gauss Seidel iteration, Cholesky’s decomposition,
476 15 Numerical Methods in Potential Theory
Fig. 15.3. Shows finite difference mesh and dipole-dipole electrode configuration
measurements; working zone and far zone., domain boundaries; cells of different
physical properties and nodes
conjugate gradient minimisation, successive over relaxation (SOR), succes-
sive line over relaxation (SLOR), LU decomposition with backward forward
substitution etc. This is a big area of mathematics and is not discussed in
this book. The solutions of these equations generate potentials at each nodal
point per one source point. Since the principle o f superposition is valid in
direct current flow field, potentials at the nodal points can be computed for
any number of sources and sinks. Each cell can be assigned different electrical
conductivity, hence it can handle problems of any degree of complication in
subsurface geometry.
15.2.2 Formulation of the Problem
Deriva tion of finite difference equation in a Cartesian coordinate for surface
measurement is presented in this section. Flow of steady current in a non-
uniform medium can be given by
−∇.
J =
∂Q
∂t
. (15.1)
This is the continuity equation for time inva riant current density
J and volume
density of charge Q. The equation ca n be written as
−∇.
σ
E
=
∂Q
∂t
(15.2)
or
−∇.
1
ρ (x, y, z)
.∇φ(xyz)
=
∂Q
∂t
. (15.3)

15.2 Finite Difference Formulation/Direct Current Domain 477
Here ρ and φ are respectively the resistivity and scalar potential. Simply we
can write the (15.2) taking
∂Q
∂t
= q(x, y, z)as
∇. [σ∇φ]+q =0 . (15.4)
If we consider this equation in a two dimensional domain assuming there is
no variation in conductivity in the y direction, i.e.,
∂
∂y
[σ (x, y, z)] = 0, (15.5)
we can write (15.4) as
∂
∂x
σ (x, y)
∂φ
∂x
+
∂
∂z
σ (x, y)
∂φ
∂z
+ q (x, z) = 0 (15.6)
where q is the current density. Hence for an element p, (Fig. 15.2) the value
of q is I / area (a b c d), or
q=
I
1
2
(h
N
+ h
S
) .
1
2
(h
E
+ h
W
)
=
4I
(h
N
+ h
S
)(h
E
+ h
W
)
. (15.7)
I is the strength of the source. Here in D.C. resisitivity finite difference mod-
elling, when intervals of the grids are same, h
N
= h
S
= h
E
= h
N
= h,and
q=4I/2h.2h =
I
h
2
. This only happens when the elements are in the sub-
surface. When the source is on the sur face, h
N
= 0 and hence q =
2I
h
2
.The
effective strength of the source is doubled when it is placed on the surface of
the earth. In practice, the grid size for discretization may not be equal and
hence the generalised equation for q is
q =4I/ (h
E
+ h
W
) hs. (15.8)
15.2.3 Boundary Conditions
The numerical solution is obtained applying the following boundary
conditions:
(a) ϕ (x, y, z) must be continuous across each element boundary of the con-
trasting physical property distribution of σ (x, y).
(b) The normal component of J
= −σ∂ϕ
:
∂n
must be continuous across ea ch
boundary.
(c) φ
i,j
(= f (x, z)) along the subsurface boundaries AB, BC and CD are zeros
as the domain boundaries are pushed far away from the working area.
Dirichlets bou ndary conditions are satisfied.
(d)
∂φ
∂z
= 0 on the air earth boundary AD . Here the Neumann boundary
condition is satisfied (Fig. 15.3).
478 15 Numerical Methods in Potential Theory
(e) q
ij
= 0 every where except at the location of the current electrodes. Here
source and sink of +q and −q are inserted. These two are the only nonzero
elements in column vector B in the matrix equation Ax = B.
(f) The grid is chosen to be rectangular with arbitrary, irregular spacing of the
nodes in the x- and z- directions respectively. The nodes in the x-direction
are labelled j = 0, 1, 2, 3,...............m and those in the z-direction,
i=0, 1, 2, 3,.........n (Fig. 15.1).
(g) The left and right edges at infinite distances in the heterogeneous half
space are simulated by the lines j = 0 and j = m respectively. .
It is possible to choose appropriate boundary conditions at infinite dis-
tance from the source and can be brought nearer with finite choice of m
and n.
(h) The Dirichlet’s boundary condition for all J = 0, 1, 2, 3 ....nwithi=0at
x=±∞ and z = ∞ is done by extending the meshes far enough away from
the sources and the conductivity inhomogeneities such that the potential
distribution approaches asymptotically to zero.
(i) Electrical conductivity distribution σ ( x, z) is assigned in each cell depend-
ing upon the nature of the problem.
(j) φ
ij,
the potentials on any surface and subsurface node (i, j) are available
with regular or irregular grid spacing in the x- and z-direction.
(k) The Neumann boundary conditio n is satisfied on the surface.
15.2.4 Structure of the FD Boundary Value Problem
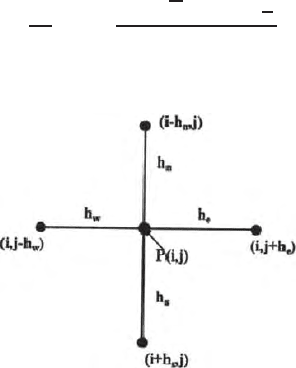
From the Fig. (15.4) [part of the grid system] we can generate the approximate
relation valid at the point P (i, j) and can write as
dφ
dx
i,j
=
φ
i,j+h
E
2
− φ
i,j−h
h
2
(h
E
+ h
w
) /2
. (15.9)
Fig. 15.4. Surrounding area of a node P
ij
with adjacent nodes
