Roy K.K. Potential theory in applied geophysics

Подождите немного. Документ загружается.

14.5 Deﬁnition of a Green’s Function 449

14.4 Adjoint and Self Adjoint Operator

In a matrix domain we can have a set of linear equations which can be

expressed in a matrix form as

n×m

m×1

n×1

(14.14)

for an n × m system where n and m are respectively the numb er of rows and

number of columns. Here A is a rectangular matrix, x is a column vector of

unknowns and b is a column vector of kn own quantities or par ameters. Its

adjoint system (Lanczos 1941) is

m×n

n×1

m×1

(14.15)

where A

is the transpose of A. A

is termed as the adjoint operator of A. If

=A=A

−1

, the matrix system is termed as a self adjoint matrix and the

operator A

is termed as the self adjoint operator. For a square symmetric

matrix we get the condition A = A

−1

For a linear o r linear diﬀerential op erator L, we deﬁne L

∗

as the com-

plex conjugate transpose of L. Taking into account the similarities in the

behaviours of a matrix and that of a linear or linear diﬀerential operator, we

deﬁne the adjoint operator as

(ψ, LΦ) = (L

∗

ψ, Φ) (14.16)

where L =

, the diﬀerential op erator. If L = L

∗

, the operator is a self adjoint

operator.

14.5 Deﬁnition of a Green’s Function

Green’s function is an inverse integral operator in a self adjoint system. It is

a response due to a source of unit strength or an unit impulse response. It

becomes a kernel function in Fredhom’s or Volterra’s integral equations.

The Green’s function is derived to ﬁnd the eﬀect of Delta function source

at a ﬁeld point. It’s form depends upon whether the point is in free space

or there is a sur face in the vicinity. Let us take a lin ear diﬀerential equation

written i n the general form as

L(r) φ(r) = f(r) (14.17)

where L(r) is a linea r, self adjoint diﬀerential operator, φ(r) is an unknown

function to be determined and f(r) is a known inhomogeneous or nonzero term.

The solution of this equation is

φ(r) = L

−1

f(r) (14.18)

450 14 Green’s Function

where L

−1

is the inverse of the diﬀerential operator and is termed as the

inverse integral operator. It is p o ssible to deﬁne L

−1

f(r) as

−1

f(r) = ∫ G(r, r

)f(r

)dr

(14.19)

where G(r, r

) is the kernel function associated with the diﬀerential operator

L. As mentioned Green’s function is a two point function and depends upon

the position of observation point a nd source point in a space domain The

self adjoint operator generates the solution of a linear diﬀerential equation

using Green’s function. Green’s function is also deﬁned as the response of a

linear system to a delta function input i.e., Green’s function of a sy stem is

the impulse response due to Dirac delta type of excitation i.e.,

LG(r, r

)=δ(r − r

). (14.20)

The response of the input δ(r − r

)isgivenbyG(r, r

)andthesource

function can be written as the combined eﬀect of this delta function with

another factor f(r

). This shows that the solution of LU = f is given by the

superposition of the Green’s function G(r, r

) with the factor f(r

). Thus we

can write

f(r) =



∞

−∞

δ(r −r

)f(r

)dr

. (14.21)

It shows that

φ(r) = ∫ G(r, r

)f(r

)dr

. (14.22)

Using Dirac delta function as an identity operator I and using the properties

of the Dirac delta function



∞

−∞

δ(r

)dr

= 1 (14.23)

we can rewrite equation (14.22) as

Lφ(r) = L



∞

−∞

G(r, r

)f(r

) dr (14.24)



∞

−∞

LG(r, r

)f(r

)dr



∞

−∞

δ(r −r

)f(r

)dr

=f(r). (14.25)

If φ(x, y) is a function of two variables x and y and L is a partial diﬀerential

operator, the Green’s function G(x, y, x

, y

) satisﬁes the equa tion

LG = δ(x − x

)(y−y

) (14.26)

14.6 Free Space Green’s Function 451

where δ(x − x

)(y− y

) represent the Diract delta function in two dimen-

sions. Let G(x, y, x

, y

) satisfy certain homogeneous boundary conditions on

a boundary in the x,y plane, then

Lφ =f(x, y) (14.27)

satisfy the same bounda ry conditions and ca n be expressed as

φ(x, y) = ∫∫G(x, y, x

, y

)f(x

, y

)dx

. (14.28)

14.6 Free Space Green’s Function

For Poisson’s problem ∆φ or ∇

φ =f(x)withφ(x) = 0 at x →∞,weget

∆G(x, y) = δ(x−y) where G(x, y) = 0 as |x−y|→∞. For a radially symmetric

space in a spherical coordinate system (see Chaps. 7 and 13)

∂

∂r



∂G

∂r



4πr

δ(r). (14.29)

The solution is

+B forr> 0. (14.30)

Here A and B are constants. S in ce G → 0asr→∞,B=0.Theoutward

normal to the surface is

∂G

∂n

∂G

∂r

. (14.31)

On the surface at r = R, one gets



2π

∂G

∂n



r=R

sin θ dθ dΨ = 1 (14.32)

where R

sin θ dθ dΨ is an elementary area on a s pherical surface (see

Chaps. 2, 3, 7, 13).

Thus,



2π

sin θ dθ dΨ = 1 (14.33)

⇒ A=

4π

φ =

4πr

4π [r − r

]

. (14.34)

452 14 Green’s Function

14.7 Green’s Function is a Potential due to a Charge

of Unit Strength in Electrostatics

Potential at a point due to a number of electrostatic charges distributed over

an entire space is obtained as a single algebraic superposition of potentials

produced at a point by each charge (see Chap. 4) . If q

, q

,..... q

are

located at distances r

, r

,.....r

respectively from the point P, the poten-

tial at P is given by

φ =

4π ∈



+ .....



4π ∈



i=1

(14.35)

where ∈ i s the electrical permittivity.

If the charges are distributed continuously throughout a region, rather

than located at discrete number of points, the regions can be divided into

elements of volume ∆v each containing charge ρ∆v, where ρ is the volume

density of charge, the potential is then given by

4π ∈

i=n



i=1

∆v

(14.36)

Equation (14.36) can be expressed in the integral form as

φ =

4π ∈



ρdv

(14.37)

The integration is performed throughout the volume where ρ has certain value.

Equation (14.37) can b e written as

φ =



ρ Gdv (14.38)

where

4π ∈ r

. (14.39)

The function G is a potential at a po int of an unit point charge and is referred

to as electrostatic Green’s function for an unbounded region.

If G(r, r

) is the ﬁeld at the observer’s point r caused by the unit p oint

source at the point r

, then the ﬁeld at ‘r’ caused by the source distribution

ρ(r

) is the integral of Gρ over the whole range of r

occupied by the sources as

shown in (14.38). Here G is the Green’s function. The inhomogeneous source

vector P is



ρ(x

, y

, z

) δ(x − x

)δ(y − y

)δ(z −z

) (14.40)

14.8 Green’s Function can Reduce the Number of unknowns 453

where

P(x

, y

, z



ρ(r

)δ(r −r

)δx

δy

δz

(14.41)

Potential function in a three-dimensional space, in terms of Green’s function,

can be written as

φ(x, y, z) =





G(x, y, z/x

, y

, z

)ρ(x

, y

, z

)dx

, dy

, dz

(14.42)

where G b ecomes a kernel function in an integral equation.

14.8 Green’s Function can Reduce the Number

of unknowns to be Determined in a Potential Problem

We can use Green’s function to ﬁnd the solution of Laplace equation ∇

φ =0

inside a required domain R bounded by a closed surface S (Fig. 14.1) when

the value of φ and

∂φ

∂n

are known over the surface. From Green’s third formula

(see Chap. 10), we get

4π





∂φ

∂n

− φ

∂

∂n





ds (14.43)

giving the value of φ at any point inside S in terms of the values Φ and

∂φ

∂n

the surface. It is well known that one gets unique solution of Laplace equation

in a bounded domain if φ and

∂φ

∂n

have prescribed values on the bounda ry. One

needs these two values at the boundary to determine φ inside. Green,s function

can be used to determine potential at a point on the boun d ary. Let φ be the

solution of Laplace equation inside the boundary S which takes the value



−



on S. Here r is the distance of the point P from the surface (Fig. 14.2). Let

G=Ψ+

. This G is the Green’s function for the point P and the surface S.

By deﬁnition, G vanishes at the boundary. One can frame a Green’s function

G=Ψ+

where Ψ is the solution of the Laplace equation inside the S. When

both φ and Ψ are harmonic we get





∂Ψ

∂n

− Ψ

∂φ

∂n



ds = 0 (14.44)

Adding this equation (14.44) to the Green’s third formula, we get

4π





Ψ+



∂φ

∂n

− φ

∂

∂n



Ψ+



4π





∂G

∂n

− φ

∂G

∂n



(14.45)

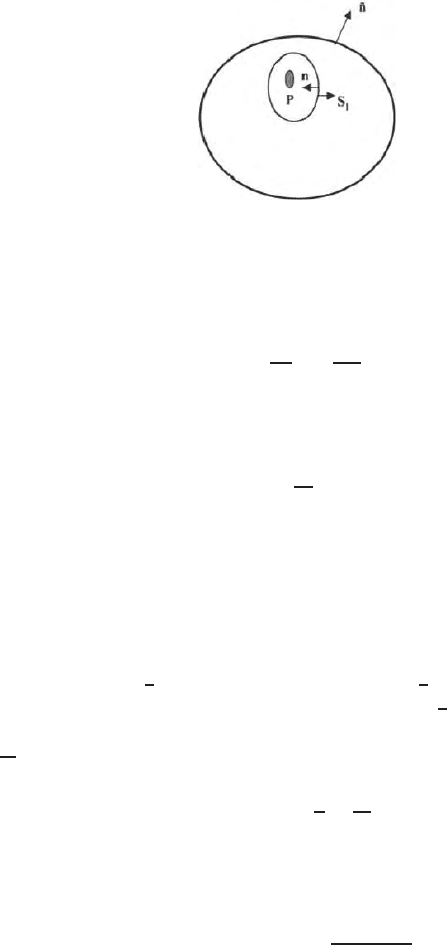
454 14 Green’s Function

Fig. 14.2. When the point P is inside the domain R; and inﬁnitesimally small circle

surround the point P to avoid singularity

where G vanishes at the boundary. Therefore, we get

= −

4π



∂G

∂n

ds. (14.46)

This is the expression f or the potential at any point inside S in terms of

Green’s function G. The properties of the Green’s function are G is harmonic

and its value vanishes on the boundary. In this section we have shown that

we can avoid determining both φ and

∂φ

∂n

on the boundary and can determine

only Green’s function to ﬁnd out the potential at any point inside the domain.

14.9 Green’s Function has Some Relation

with the Concept of Image in Potential Theory

When a source point P and an observation point Q a re within the region S, we

can write G(P, Q) =

+Ψ(P, Q) where Ψ(P, Q) = −

such that G (P, Q) = 0

on the surface as mentioned earlier. Potential at Q is

due to a unit source

of charge at P. The potential at Q (ξ, η, ζ) due to the image point P

′

of P

is −

. Green’s function for an inﬁnite plane is (Figs. 14.3, 14.4)

G(P, Q) =

−

. (14.47)

When the observation point is on the surface i.e., when r = r

′

,G(P, Q) = 0.

If the Green’s function is known, the Dirichlet’s problem can be solved. In

equation

4πφ

= −



φ(P, Q)

∂G(P, Q)

∂n

ds. (14.48)

We have

=(ξ − x)

+(η − y)

+(ζ −z)

(14.49)

and

′2

=(ξ

′

− x)

+(η

′

− y)

+(ζ

− z)

. (14.50)

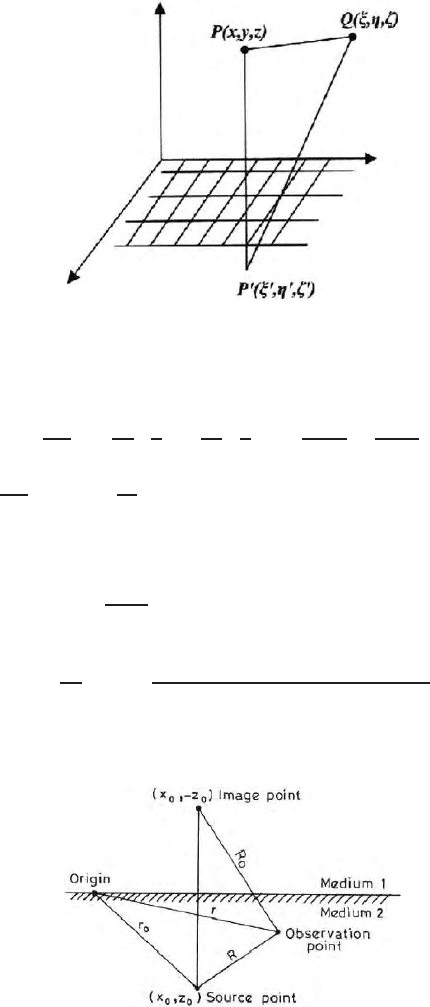
14.9 Green’s Function has Some Relation 455

Fig. 14.3. Concept of image in analytical continuation

Here

∂G

∂n



∂

∂z



−

∂

∂z



ζ −z

−

ζ +z

(14.51)



∂G

∂n



z=0

= −

. (14.52)

Therefore, potential at any point is

4πφ

=2z



∞

φ(Q)

⇒ φ

2π

∞



−∞

∞



−∞

φ(ξ

, η

)dξ

dη



(ξ

− x)

+(η

− y)



1/2

. (14.53)

Fig. 14.4. Shows the concept of image in Green’s Function domain in presence of

a boundary between the two media

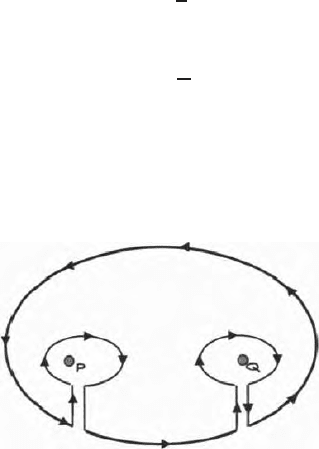
456 14 Green’s Function

This is the simplest example of application of Green’s function in Poten-

tial theory. Equation (14.53) shows that if a p otential is prescribed on the

boundary, we can ﬁnd out potential at any point in the region. Thus one gets

a scalar potential ﬁeld upward analytical continuation formula from Green’s

function.

Figure 14.4 shows the position of the observation point in the presence of a

source and its image and a plane horizontal boundary between a medium 1 and

2. Computation of potential at the observation p oint as shown in chapter 11

can also done in Green’s function domain.

Problems 1 and 2 in Sect. 14.14 are some of the examples.

14.10 Reciprocity Relation of Green’s Function

In this section we show that the principle of reciprocity is valid for Green’s

function and the symmetry exists in the behaviour of the Green’s function.

If P and Q are the two points inside a region bounded by a surface S and

G (P, Q) shows the value of the Green’s function at Q for point P and surface

S, then G(P, Q) = G(Q, P) (Fig. 14.5).

Applying Green’s theorem (10.8) to the region bounded by S, S

and S

where S

and S

are the surfaces of the spheres of inﬁnitesimal small radii r

and r

having their centers at P and Q. We put

φ =G

′

+Ψ

and

′

′′

′

+Ψ

′

where r and r

′

are the distances of the points of observation from the points

PandQ.HereG

′

and G

′′

are respectively the Green’s functions for P and S

as well as for Q and S. We have from Green’s theorem

Fig. 14.5. Reciprocity Relation of Green’s Function

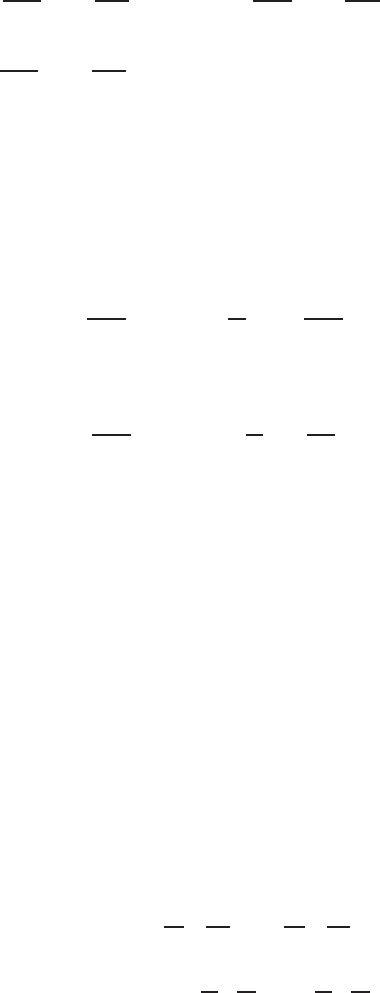
14.11 Green’s Function as a Kernel Function in an Integral Equation 457





′

∂G

′′

∂n

− G

′′

∂G

′

∂n



ds +





′

∂G

′′

∂n

− G

′′

∂G

′

∂n







′

∂G

′′

∂n

− G

′′

∂G

′

∂n





′

∇

′′

− G

′′

∇

′

)dv (14.54)

Since Ψ and Ψ

′

are the solutions of Laplace equation and since P and Q have

been excluded from the region of volume of integration, therefore ∇

′

0, ∇

′′

= 0. Otherwise also Green’s functio n is a harmonic function. The

right hand side of equation (14.54) is zero. By deﬁnition G

′

and G

′′

vanish

on the boundary S, so tha t the ﬁrst integral on the left is zero. In the second

integral on the left, we put ds

dω where dω is the element of the solid

angle. Hence



′

∂G

′′

∂n





+Ψ



∂G

′′

∂n

dω (14.55)

tends to zero, when r

→ 0 and Ψ is assumed to be ﬁnite. Again

−



′

∂G

′′

∂n

= −





+Ψ

∂Ψ

∂n



dω (14.56)

tends to zero as r

→ 0. The integral reduces to –4πG

′

where G

′

denotes

the value of the Green’s function at P for Q and S, i.e. G (Q, P). Simi-

larly the third integral r educes to G (P, Q) which is equal to G (Q, P).

Thus the principal of reciprocity is valid for Green’s function i.e., G(P, Q) =

G(Q, P). It is also mentioned as the symmetrical property of the Green’s

function.

14.11 Green’s Function as a Kernel Function

in an Integral Equation

In this section we shall show how Green’s function appears in an integral

equation in electrostatics or direct current ﬂow ﬁeld. This derivation is given

by Eskola (1979, 1992), Eskola and Hongisto (1981).

In direct current ﬂow ﬁeld, the govering equations are (i) Laplace equation

∇

φ = 0 and Poisson’s equation ∇

φ = ρ/ ∈. The boundary conditions are

= φ

and



∂φ

∂n





∂φ

∂n



(14.57)

on the surface S and φ

= φ

and



∂φ

∂n





∂φ

∂n



at the boundary

A (Fig. 14.6). The product Rφ is bounded as φ is a regular function. The

regularity condition i.e., RG is bounded as R tends to inﬁnity. (See Chap. 10).

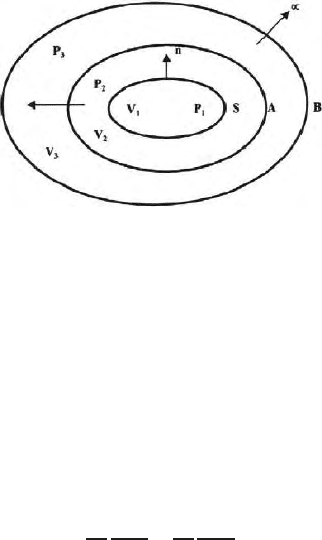
458 14 Green’s Function

Fig. 14.6. Bounded domain with the outer boundary goes to inﬁnity

The boundary value problems based on Laplace or Poisson’s equation can

be converted into an integral equation using Green’s theorem and Green’s

function. In Green’s function domain the basic equations are

∇

G(r, r

)=−δ(r −r

) (14.58)

where δ is the dirac delta function. The solution of which satisfy the boundary

conditions.

∂G

∂n

∂G

∂n

(14.59)

on the surface A (Fig. 14.6).

Green’s function from these t wo equations can be written as sum of the

two terms.

G=G

. (14.60)

Here

(r, r

)=1/ (4π(r −r

)) (14.61)

is a free space or whole space Green’s function. In

∇

G=−δ(r − r

). (14.62)

is a singular function at r = r

. This function is regular at inﬁnity and

together with its derivatives will automatically be continuous on A. The func-

tion G

is a nonsingular function and is a solution of the Laplace equation

∇

= 0 that satisﬁes boundary conditions (14.59) on the surface A. The

method of deducing an integral equation representation.

Φ(r) =



G(r, r

)ρ(r

)dv

(14.63)

from the diﬀerential equation and the boundary condition is based on the

application of Green second identity. Green’s formulae are valid for two scalar