Roy K.K. Potential theory in applied geophysics

Подождите немного. Документ загружается.

14.11 Green’s Function as a Kernel Function in an Integral Equation 459

functions as discussed in Chap . 10 which together with their ﬁrst and second

derivatives are continuous in a closed region and on the surface. Singularities

at points and along lines can occur and the problem is then treated by suitably

isolating the singularities. Substituting φ and G into Green’s second identity

and applying it to region v

and v

interior to the boundary A (Fig. 14.6).

We get





∇

− φ

∇



dv =





∂φ

∂n

− φ

∂G

∂n



(14.64)

where r

is in v

and r is in v

and the operations are performed with

respect to the variable R. Substituting Poisson’s equation ∇

φ = −

∈

and

∇

G=−δ(r − r

), the results in the previous equation acquires the form

∈



ρdv +





∂φ

∂n

− φ

∂G

∂n



dA. (14.65)

Applying Green’s second identity to the region v

exterior to the surface A

and keeping r

in v

, the volume integral on the left hand side of Green’s

identity vanishes because φ and G both satisﬁes Laplace equation in v

.The

integral over the outermost surface B, approaches zero as B recedes to inﬁnity.

Green’s second identity thus takes the fo rm





∂φ

∂n

− φ

∂G

∂n



ds (14.66)

Since φ satisﬁes boundary conditions (14.59), we can eliminate unspeciﬁed

values of φ and its normal derivatives on the boundary.

Multiplying equation (14.65) by

(Escola 1992) and adding it to equa-

tion (14.66), we get

φ =

∈



ρdv +





∂φ

∂n

− φ

∂G

∂n



−

∂φ

∂n

∂G

∂n

. (14.67)

Substituting the boundary conditions (14.59) , the surface integrals of (14.65)

vanishes. Interchanging the variables r as r

and using the reciprocity property

of Green’s function G(r, r

)=G(r

, r). The potential φ reduces to

φ(r)=

∈



G(r, r

)ρ(r

)dv

(14.68)

where the integration is around the volume v

(Fig. 14.6) and the surface S

ρ, the charge density in electrostatics and resistivity in direct current ﬂow

ﬁeld is around the source at r

460 14 Green’s Function

Thus we have seen in this section that Green’s function appears as a kernel

in an integral equation.

14.12 Poisson’s Equation and Green’s Function

Let

Lφ = f(r) (14.69)

in the domain R.

φ = k(r) on the boundary S. (14.70)

L is the Laplacian operator ∆ or ∇

. For an n dimensional problem G(r, r

)

is the Green’s function for the source point at r and the observation p oint at

where r = (r

, r

,...r

)andr

, r

...r

). Hence

LG(r, r

)=δ(r

− r

) δ(r

− r

) δ(r

− r

) ....+ δ(r

− r

) (14.71)

for an n dimensional hyperspace. This equation is valid for all the values of r

and r

in the domain R and G(r, r

) = 0 on the boundary for all r

on S and

all r in the domain R (Fig. 14.1). The n dimensional Laplacian operator is

∇

∂

∂r

∂

∂r

∂

∂r

...+

∂

∂r

. (14.72)

Since

∇(Ψ∆φ − φ∇Ψ) = ∇Ψ.∇φ +Ψ∇

φ −∇Ψ .∇φ − φ∇

Ψ (14.73)

when both Ψ and φ are harmonic and scalar potential functions (see Chap. 10),

we can write

Ψ∇

φ = φ∇

Ψ+∇(Ψ∇φ −φ∇Ψ) (14.74)

Integrating and applying Gauss’s divergence theorem, we can write





Ψ∇

φdv =





φ∇

Ψdv +





∂φ

∂n

− φ

∂Ψ

∂n



ds (14.75)

where dv and ds are respectively the elements of volume and surface. Equa-

tion (14.75) can be written as





G(r, r

′

)f(r)dv





k(r)δ(r − r

′

)dv

−



k(f)

∂G(r, r

′

)

∂n

(14.76)

Since Ψ = G(r, r

) is zero on the surface.

Hence

14.13 Problem 1 461

φ(r) =





G(r, r

′

)f(r)dv +



k(r)

∂G(r, r

′

)

∂n

ds (14.77)

For a three dimensional Euclid ean space

∇

G(r, r

)=δ(r

− r

)δ(r

− r

)δ(r

− r

) (14.78)

We can then summerise on the conditions for application of Green’s function

for solution of Poisson’s equation as

(i)

∇

φ = f(r) within the domain R (14.79)

(ii)

G(r, r

) = 0 on the surface S (14.80)

(iii)

∇

G(r, r

)=δ(r −r

) (14.81)

(iv)

φ = f(r) on the surface S (14.82)

(v)

G(r, r

) < 0 within the domain R

(vi)

φ(x) =





G(r, r

)f(r)dv +





k(r)

∂G(r, r

)

∂n

ds (14.83)

(vii) G is harmonic inside the domain and outside except on the surfa ce

where it becomes zero. G approaches zero also at inﬁnite distance from

the source.

(viii) It is also a regular function at inﬁnite distance from the source. In this

section it can be shown that Green’s function can be used for solution of

Poisson’s eq uations satisfying the Dirichlet, Neumann and mixed bound-

ary conditions.

14.13 Problem 1

A highly conductive body of conductivity σ

and of arbitrary shape is assumed

in a homogenous half space of conductivity σ

,whereσ

≫ σ

. The conductive

body is charged with direct current I. What will b e the potential at any point

in a medium or on the surface?

Highly conductive body has become a source of current as soon as it is

charged with direct current and the outer surface of the body b ecomes an

equipotential surface. The charged body in a medium 2 (earth )will have an

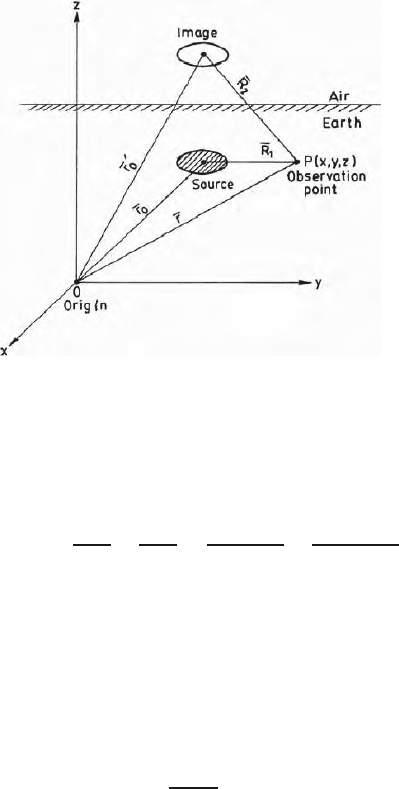
462 14 Green’s Function

Fig. 14.7. Source and its image for solution of a problem in Green’s function domain

image in medium 1(air). Figure 14.7 shows the geometry of the conductive

body, the source, its image in the air, the observation point and the assumed

origin of the problem. The Green’s function for this problems is

G(r, r



¯



¯



|(¯r −¯r





¯r −¯r





(14.84)

where

=¯r −¯r

and

=¯r −¯r

The potential at a point P(x, y, z) due to the stationary current is given by

φ(¯r) = φ

(¯r) +

4π ∈



G(r, r

)ρds (14.85)

where ρ is the volume density of charge, G(r, r

) is the Green’s function of

the problem, ∈

is the free space electrical permittivity and φ

(¯r) is the free

space potential in the absence of any kind of inhomogeneity in half space.

The integration is done over the surface S of the conductor. The boundary

conditions for this problem are

(i)

ρ =D

− D

(14.86)

(see Chap. 4)

14.14 Problem 2 463

where D

and D

are the normal components of the displacement currents.

Since



D=∈



E, we can write

ρ =∈

/σ

− J

/σ

) (14.87)

where J

and J

are the normal components of the current density vectors

and they are continuous across the boundary i.e., J

.Fromequa-

tion (14.87), we get

ρ =∈



−



(14.88)

Thus the equation (14.88) b ecomes after substituting the value of ρ

φ(¯r) = φ

(¯r) +

4π ∈

. ∈



G(r, r

)



−



ds (14.89)

Equation (14.89) can be rewritten as

φ(¯r) = φ

(¯r) +

4π



G(r, r

)Q J

ds (14.90)

where Q =

−

since

≈ 0forσ

≫ σ

Thus :

φ(¯r) = φ

(¯r) +

4πσ



G(r, r

ds (14.91)

(¯r) is the potential at a point P(x, y, z) due to an homgeneous half space

for a source at a distance ¯r. Green’s function G(r, r

) will vary from problem

to problem. Substituting the value of G(r, r

) for this problem from (14.84)

one will get an integral to be solved analytically or numerically using Gauss

quadrature or Simpson’s rule or Weddles rule. In case analytical solutions of

the integrals are not p ossible one has to choose one of the said numerical tools.

Author prefers 7 point Gauss Quadrature for getting a reasonably accurate

answer. It is a simplest example to show how Green’s function can be used

for solving problems in potential theory.

14.14 Problem 2

An homogeneous half space is divided into two compartments of resistivity ρ

and ρ

. A vertical wall separates the two compartments. (Fig. 14.8). Source of

current is in the medium 1. The source point S

has images at S

in medium

2andS

in medium 0 of resistivity ρ

(air). The image S

will have an image

in medium 0. Therefore, one vertical contact in the subsurface generates

three images. For solution of this problem in the Green’s function domain the

guiding equations are

(i)

∇

= −δ(¯r

′

−¯r

′

) (14.92)

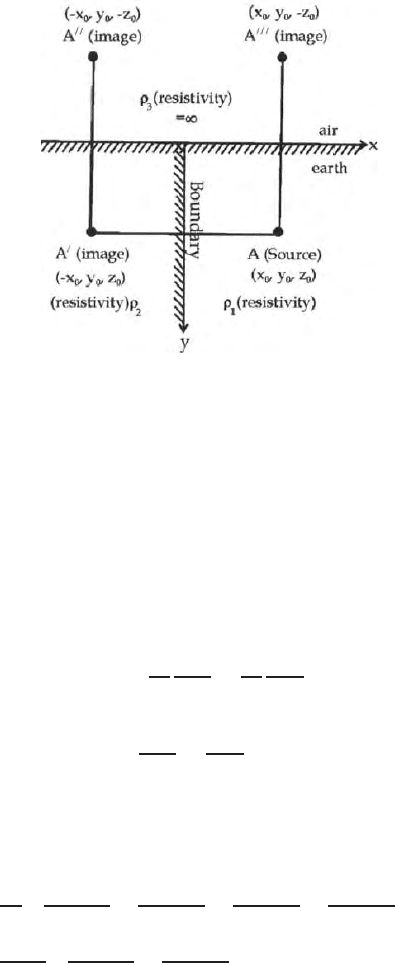
464 14 Green’s Function

Fig. 14.8. A source in a medium of resistivity ρ

faces an air-earth boundary along

the vertical z direction and vertical boundary between the two media of resistivities

and ρ

along the horizontal × direction

(ii)

∇

= 0 (14.93)

and the boundary conditions are

(i)

(14.94)

(ii)

∂G

∂n

∂G

∂n

(14.95)

On the vertical contact

∂G

∂n

∂G

∂n

= 0 (14.96)

On the ground surface

= 0 (14.97)

The Green’s function in the two media are

4π



|¯r

′

−¯r

|¯r

′

−¯r

|¯r

′

−¯r

|¯r

′

−¯r



(14.98)

1+k

4π



|¯r

′

−¯r

|¯r

′

−¯r



. (14.99)

Here the coordinates of the source and images are (Fig. 14.8)

14.15 Problem 3 465

¯r

=(x

, y

, z

)

¯r

=(−x

, y

, z

) (14.100)

¯r

=(−x

, y

, −z

)

¯r

=(x

, y

, −z

)

and k is the reﬂection factor (see Chaps. 8 and 11)

k=(ρ

− ρ

)/(ρ

+ ρ

14.15 Problem 3

A perfectly conducting body is placed in an homogeneous and isotropic earth.

Find the potential at any point on the surface or at any p oint in the half space.

A conducting homogeneous and isotropic earth is assumed as an half space

over which a non conducting half space ﬁlled with air (ρ

air

= ∞). A perfectly

conducting body is placed in a homogeneous earth. A d irect current source of

strength I is applied directly to the body. In the internal region V

= constant,

i.e., φ

= φ

. In the external region V

satisﬁes Laplace equation in all the

regions of uniform conductivity, i.e., ∇

= 0. Potentials satisﬁes all the

boundary conditions on all the surfaces of conductivity discontinuity i . e.,

(i)

= φ

(14.101)

(ii)

∂φ

∂n

= σ

∂φ

∂n

(14.102)

(iii) Rφ and RG are regular functions in the potential and Green’s function

domain at inﬁnity.

(iv) Both potential and Green’s function are harmonic functions both in the

internal and ext ernal region. On the boundary φ is a continuous function

but G is a singular function.

Starting equation of this problem in the Green’s function domain is

∇

G(¯r, ¯r

)=−4πδ(r −r

) (14.103)

It satisfy the boundary conditions speciﬁed above.

Applying Green’s second identity (see Chap. 10), we get





'

(¯r

)∇

G(¯r, r

) −G(¯r,¯r



∇

(¯r

)

(





(¯r)

∂

∂n

G(¯r, ¯r

) −G(¯r,¯r

)

∂

∂n

(¯r)

. (14.104)

466 14 Green’s Function

Since the potential must be continuous across the surface of the conductor,

the ﬁrst integral can be written as

4π



)

∂

∂n

G(¯r, ¯r

)dS

(14.105)

⇒

4π



∂

∂n

G(¯r, ¯r

)ds

(14.106)

⇒

4π



div grad G(¯r,¯r

)ds

(14.107)

applying Gauss’s divergence theorem. Therefore (14.107) can b e rewritten as

= −

4π





∇

G(¯r, ¯r

)=0. (14.108)

Since G is harmonic in the external region.

(¯r) = −

4π



G(¯r, ¯r

)

∂

∂n

(¯r

)ds

. (14.109)

Since



J=σ



EandI=





J.n .ds (see Chap. 6)

We can write



(¯r

)

∂

∂n

.φ

). (14.110)

14.16 Dyadics

Dyadic Green’s f u n ction are also called tensor Green’s function because it has

nine components similar to that of a 3 × 3 second order tensor. Tai (1971)

gave a detailed account about the properties of dyadics and the dyadic Green’s

function.

Dyad means a group of two quantities and a dyadic is a g roup of two

vectors i.e.,

−→



B. (14.111)

Use of dyadic Green’s function in solving geophysical b oundary value problems

using integral equation method are discussed in detail by Hohmann (1971,

1975, 1983, 1988), Weidelt (1975), Raiche (1975). Ting and Hohmann (1981)

Das and Verma (1981), Beasley and Ward (1986), Meyer (1976).

A vector can be written in the cartisian coordinate as

⇀



x

(14.112)

14.16 Dyadics 467

where D

s are scalar comp onents along the x, y, z directions and represent the

three unit vectors along the three directions for i = 1, 2, 3. For three distinct

vectors along the three directions, we can write

⇀



i=1



, for j = 1, 2, 3 (14.113)

and a dyadic function is denoted by



D and is deﬁned as denoted by

−→





j=1



(14.114)

where



are the three vector components of

−→



Dforj=1, 2, 3. We can write

−→



−→







(14.115)

where



are the nine scalar components of

−→



Dandx

x

are the nine pairs

of the unit dyadics. Each of these dyadics are formed by a pair of two unit

vectors in mutually orthogonal direction (Tai – 1971).

Therefore, we can write as

−→



⎡

⎣

xxA

xyA

xz

yxA

yyA

y

←

zxA

zyA

zz

⎤

⎦

. (14.116)

Important P roperties of the dyadic Green’s function are

(i)

−→



I=x

x

+ x

x

+ x

x

(14.117)

where

−→



I is the unit dyadic or idem factor. Here

−→



−→



−1

= I

−→



−1

−→



D = I (14.118)

where

−→



−1

is the reciprocal of the dyadic

−→



(ii) Dyadic is deﬁned by two vector

−→



B as mentioned where functions,

i.e.



Aand



B ar e respectively deﬁned as the anterior and posterior vectors

and its transpose is given by

−→



A (14.119)

468 14 Green’s Function

Green’s function is dyadic for a vector source and is nondyadic for a scalar

source. For vector source also th e Green’s function formula is derived to ﬁnd

the eﬀect of the Dirac delta function. In a similar way, as the scalar Green’s

function, its form depends upon whether the point is in the free space or there

is a surface is the vicinity.

For a time varying vector source, the electric and magnetic potentials

are vector potentials say which satisfy the Helmholtz electromagnetic wave

equation as

∇



A −γ



A=−



J (14.120)

where γ is the propagation constant. For a delta function source



J is r eplaced

by (u

)δ(r−r

)where(u

) are the unit vectors along the x,

y and z directions. For a spherically symmetric free spa ce the vector potential

−γ|r−r

4π |r −r

. (14.121)

This is considered as the vector Green’s function i.e.,



G(r, r

−γ|r−r

4π |r −r

(14.122)

where the vector potential is derived for a spherical l y symmetric free space

(Chap. 13).

For a general current distributions



J, the solution is obtained by a superpo-

sition integral using the conditions that x, y and z components of the current

densities J

respectively are associated with the unit vectors u

the Green’s function domain. This rule is readily taken into account by intro-

ducing the dyadic Green’s function which is the solution of

∇

−→



G(r,r

) −γ

−→



G(r,r

)=−

−→



I δ(r − r

) (14.123)

where

−→



G(r −r

) is the dyadic Green’s function,

−→



I is the idem factor or unit

dyadic (u

). For a spherically symmetric free space the solution

of (14.122) is

−→



G(r,r

−→



−γ|r−r

4π |r −r

. (14.124)

and the vector potential in dyadic space is given by



A(r) =





−→



G(r, r



J(r

)dv

(14.125)

We can write the three components of the dyadic Green’s function as