Романовский С.И. Седиментологические основы литологии

Подождите немного. Документ загружается.

•странно) его разработанностью применительно к задачам ритмо-

литологического анализа.

Назовем

лишь некоторые публикации, либо принадлежащие

перу «законодателей терминологических

мод»

(выражение

Н. Б. Вассоевича и И. Г. Гладковой

[45]),

либо те, в которых

интересующая нас проблематика освещена достаточно обсто-

ятельно: Ю. А. Жемчужников [111, 112, 113]; С. Н. Бубнов [331;

Л.

Б. Рухин

[258],

В. Е. Хаин [312, 316], Р. Шрок

[339],

Н. Ф. Балуховский [16], Г. А. Иванов

[129],

А. Б. Вистелиус

[51],

И. А. Одесский

[206],

Ю. И. Возовик [65], А. В. Зуб-

ков

[128],

П. Дафф, А. Халлам, Э. Уолтон [951, Г. Ф. Лунгерс-

гаузен

[183],

С. В. Калесник

[131],

А. В. Шнитников

[337],

В.

Штайнер [548] и, наконец, обстоятельный обзор Н. Б.

Вас-

соевича и И. Г. Гладковой [45] *.

Для того чтобы по возможности глубже уяснить

причины

такого положения дел, целесообразно соотнести все отмеченные

выше

понятия

с двумя уровнями познания: эмпирическим и теоре-

тическим.

На эмпирическом уровне исследованию подвергается кон-

кретная осадочная толща, которая рассматривается как реализа-

ция процесса осадконакопления. Причем знания самого процесса

(его

механизма, временной продолжительности и т. п.) не пред-

полагается. Если строго придерживаться такого подхода, то все

употребляемые при ритмолитологическом анализе

понятия

не

должны выходить за рамки их узко эмпирической трактовки

том смысле, что в их определении не должны фигурировать такие

понятия, смысл которых может быть уяснен только при разра-

ботке теоретических моделей. В частности, это касается

«вре-

мени»

в смысле прямого соотношения реализации процесса,

одной стороны, и условий протекания самого процесса —

о другой.

Действительно, рассмотрим некоторые подходы к определению

интересующих нас понятий, в которых это очевидное требование

не выполняется. «Ритм означает для всех

явлений

не просто

периодическое повторение, а именно равномерное повторение,

через равные промежутки времени» [111, с. 75]. Если же времен-

ные промежутки неодинаковы, то (по Ю. А. Жемчужникову)

это уже не ритмичность, а цикличность. Но как, не располагая

.моделью процесса осадконакопления, а имея дело лишь с его

реализацией (т. е. с разрезом), определить, одинаковыми или

неодинаковыми были временные промежутки, требующиеся

для формирования двух смежных ассоциаций пород, остается

неясным. Говоря же более строго, задача «восстановления»

Когда рукопись была в работе, нам стало известно, что в Новосибирске

на Всесоюзном совещании по

цикличности

геологических

явлений

было

сделано много интересных докладов, связанных с терминологией. В частности,

мы имеем в виду доклад Г. А. Иванова, А. В. Македонова, Н. В. Ивапова

и другие.

интересующих пас временных интервалов на чисто эмпириче-

ском уровне вообще неразрешима.

Более или менее сходных определений придерживался Л. П. Ру-

хни

[258],

который предложил, в частности, длительный по

вре-

мени формирования ритм именовать «периодом», в то время как

С.

В. Калесник [131] «периодом» называет ритмы одинаковой

продоляхителыюсти, а А. Б. Вистелиус [51, с. 1751 считает, что

«размер

ритма определяется его периодом... Чем больше период

ритма, тем он более высокого порядка». Ю. А. Жемчупши-

ков

[113],

А. В. Шниттшков

[337],

а также Н. Б. Вассоевич

и IL Г. Гладкова [45], по сути дела, отождествляют такие понятия,

как «ритмичность» и «периодичность», очевидно, не находя ре-

ального смысла для их разделения. Г. А. Иванов же 1129, с. 14]

поясняет: «Термины

«ритм»

и «ритмичность» более правильно

(в

каком смысле? — С. Р.) отражают периодическую и именно

ритмическую ... повторяемость явлений в природе, чем термины

«цикл»

и «цикличность». Г. Ф. Лунгерсгаузеп [183] настаивал

на том, чтобы синонимом периодичности считать не ритмичность,

цикличность. Наконец, Н. Ф. Балуховский [161, очевидно,

во

избежание разночтений предложил объединить два термина

«цикл»

и «период» и циклы продолжительностью 34—45 млн. лет

впредь именовать «циклопериодом» (? — С. Р.). Столь же не-

удачно, с пашей точки зрения, предложение И. А. Вылцана [721

о введении понятия

«ритмогамма».

Если следовать такому прин-

ципу конструирования понятий, то чем хуже, например,

«ритмо-

цикл»,

«ритмопериод» или «циклоритмоповтор»?

1973 г. с обстоятельным обзором и критикой современной

«термикклатуры»

(термин М. Г. Бергера), употребляемой при

анализе строения разрезов осадочных толщ, а также при изучении

процессов нефте- п газообразования, выступили IL Б. Вассоевич

и П. Г. Гладкова [45]. В их работе отстаивается по существу тезис

глобальной формализации понятийной базы, т. е. требование

того,

чтобы такие понятия, как

«ритм»,

«цикл»

«период»,

упо-

треблялись всегда в единственном смысле вне зависимости от того,

к каким геологическим дисциплинам и к какому классу задач

пределах этих

дисциплин

относятся указанные понятия.

Вообще

говоря, такое требование вполне законно, тем более

что эти понятия не являются геологическими, а заимствованы

из других наук, где они имеют, как правило, однозначное толко-

вание. II тем не менее обращение к опыту этих наук, к сожалению,

существа

дела не меняет:

«ритм»,

«цикл»,

«период» и другие род-

ственные им понятия, по-прежнему, остаются многозначными

и не имеющими ясного смысла.

Суть

дела, очевидно, заключается в том, что изначально эти

понятия являлись обычными знаками обиходной речи и как всякие

такого рода знаки имели лишь этимологическое толкование.

Когда

же эти понятия взяли на вооружение такие науки, как

механика

(«цикл»,

«период»),

математика

(«период»)

и др., то

рамках этих

дисциплин

они

получили

четкие определения,

и к тому же были развиты конкретные операциональные процедуры

соотнесения этих: определений с конкретным классом объектов.

Иными словами, было установлено взаимооднозначное соответ-

ствие

между определениями этих:

понятий

и соотносимыми с

ними

объектами.

геологии сложилась

иная

ситуация. Вначале была под-

мечена повторяемость отдельных объектов и

явлений

(ассоциаций

пород, чередования трансгрессивных и регрессивных этапов

развитии бассейнов осадконакопления и т. п.), а уж затем стали

приписывать выделенным объектам то или шиЗе наименование:

•«ритм»,

«цикл»,

«период» и т. д. Причем в обоснование, как пра-

вило,

приводится опыт обращения с этими понятиями в других

научных дисциплинах. Но там, как мы видим, эти понятия

вво-

дятся

(по определению), в геологии же их пытаются вывести путем

анализа

конкретных объектов, т. е. стараются установить одно-

значное соответствие между определенным классом геологических

объектов

и понятиями, которые в других науках связываются

объектами или явлениями другой природы, и перенести их

смысловую

нагрузку на геологические объекты. Такой анализ

ясности в словоупотребление пока не внес, да, вероятно, п в прин-

ципе

внести не может.

!Многие геологи, очевидно, не видя реальной возможности

что-либо изменить в сложившейся ситуации, вообще не признают

смыслового

различия таких понятий, как «ритмичность» или

«цикличность»,

считая, по всей вероятности, что оно по

крайней

мере

не влияет на существо дела. Такую позицию на протяжении

уже

многих лет занимает, например, В. Е. Хаин [312,

3161.

К нему

примыкают Н. В. Логвиненко и М. И. Ритенберг

[176],

а также

американские геологи П. Дафф, А. Халлам и Э. Уолтон [95].

Определения, четко соответствующие эмпирическому уровню

познания, можно найти в работах А. Б. Вистелиуса [51],

Р. Шрока

[3391,

Ю. И. Возовика [651, В. Штайнера [548] и дру-

гих геологов. Так, А. Б. Вистелиус [51, с. 175] пишет: «Ритм —

повторение определенных черт строения разреза через интервалы

более

или менее постоянной длины». Ю. И. Возовик [65, с. 8]:

«Ритм

— соразмерность, стройность, — характеризует законо-

мерное чередование соизмеримых элементов в системе». Р. Шрок

[339,

с.

36—37]:

«Ритмичность..., т. е. определенный литологи-

ческий

порядок, или порядок структуры (разреза. — С. Р.),

junoro

раз повторяющийся в одной

секции

или в бассейне отло-

жения».

Эмпирически сложившийся опыт геологии удачно выразил

В.

Штайнер

[548],

который под осадочными циклами предлагает

понимать закономерные повторения по вертикали симметрично

построенных

(курсив наш. — С. Р.) породных ассоциаций, а под

ритмами — последовательность несимметричных ассоциаций

пород.

Действительно, геологи, изучающие разрезы угленосной фор-

мации, устойчиво повторяющийся набор пород, который включает

породы как трансгрессивного, так и регрессивного ряда, привыкли

именовать «угленосными циклами». В то же время

типично

фли-

шевый ассортимент пород (многослой) включает в себя породы

только трансгрессивного ряда и с легкой руки II. Б.

Вассое-

вича [36] пока большинством геологов именуется «флишевым

ритмом».

конечном итоге дело не в том, существуют или не существуют

различия между понятиями

«цикл»

«ритм»

(их с равным успехом

моя-хно видеть или не замечать), а в том, в каком смысле эти поня-

тия используются в каждой конкретной задаче и соответствует ли

придаваемому этим понятиям смыслу интерпретация полученных

результатов

ритмолитологического анализа.

Легко понять, что последнее требование может быть достигнуто

только в том случае, если, во-первых, данные

понятия

будут

вве-

дены «по определению» и, во-вторых, на базе этих

понятий

будет

развита

конструктивная теория, позволяющая их использовать

рамках широкого класса задач, общих для большей части гео-

логических

дисциплин.

Если первое условие можно назвать необ-

ходимым, то второе уже достаточно для того, чтобы прекратить

многочисленные дискуссии по поводу выяснения «истинного»

смысла таких понятий, как

«повторяемость»,

«ритмичность» и

«цикличность».

Если исследование закономерностей строения разрезов ведется

на теоретическом уровне, то оно предполагает

наличие

модели

которой процесс слоенакопления реализуется по схеме пери-

одического процесса (в общем случае), что позволяет вычисленные

теоретическим путем характеристики процесса — амплитуду

период, фазу и частоту — сравнивать с эмпирическими оценками

этих характеристик на материале предварительно арифметизиро-

ванных разрезов осадочпых толщ. Иными словами, в такой поста-

новке подразумевается не «восстановление» характеристик про-

цесса

по его предполагаемым реализациям, что в общем виде

сделать невозможно, а задание или в крайнем случае подбор этих

характеристик, наилучшим образом (например, в смысле квадра-

тического отклонения) соответствующих эмпирическому мате-

риалу.

Ясно,

что для реализации этой схемы прежде всего необходимо*

знание геологической

специфики

исследуемого материала, т. е.

обоснованные предполояления о периодической (или квазипериоди-

ческой) структуре процесса, генерировавшего накопление сло-

истых толщ. Только в этом случае оправдай попек «скрытых

закономерностей» в строении разрезов и только при этом возможна

обоснованная интерпретация выявленных характеристик процесса

осадконакопления. При отсутствии же такой модели, построенной

пусть и на чисто геологическом уровне, найденные значения

параметров являются следствием аппроксимации временного ряда

(последовательность

арифметизированных характеристик

раз-

реза

трактуется как временной ряд) тем или иным аналитическим

выражением и никакой геологической интерпретации, строго

говоря,

не допускают.

Если

в исследуемых разрезах наблюдаются отчетливо выра-

вненные ритмичность (флнш) или цикличность (угленосная форма-

ция), то в первом приблил^ении можно полагать, что они явились

следствием периодического процесса,

все последующие постро-

ения

необходимо осуществлять, опираясь на это предполоях'ение.

Однако в общем случае наблюдаемая в разрезах ритмичность

далеко не всегда является реализацией периодического процесса.

Для того чтобы убедиться в справедливости высказанного поло-

жения, рассмотрим с этих позиций механизм флишевой седи-

ментации.

настоящее время, как известно, распространены две конку-

рирующие гипотезыфлишенакопления: осцилляционная Н. Б. Вас-

ооевича

[41] и мутьевых потоков Ф. Кюнена

[467].

Осцилляционная гипотеза предполагает квазипериодические

колебания земной коры, фиксирующие в разрезе правильную

ритмичность или квазиритмичность флигпа. Такая трактовка

значительно ослояшяет генетическую интерпретацию флишевой

седиментации, так как не удается выяснить

причину

отсутствия

этих правильных колебательных движений за пределами трога.

Правда,

автор гипотезы — Н. Б. Вассоевич — оставил одну

ч<степень

свободы» для тех, кто не полностью ее разделяет, пред-

положив, и не без оснований, что между отложениями смежных

ритмов могут быть значительные паузы в седиментации и их

продолжительность может быть более значительной, чем время,

течение которого образуются слои единичного флишевого много-

слоя.

Если эта мысль справедлива, то ее можно интерпретировать

двояко:

либо паузы на фоне восходящих колебаний, сопровожда-

ющиеся

частичным размывом ранее отложившегося осадка, либо

паузы

на фоне нисходящих двиячений земной коры (перерыв в осад-

конакоплении). Если согласиться со вторым предположением, то

следует считать флишенакопление не непрерывным (как утвер-

ждают

сторонники осцилляционной гипотезы), а дискретным

процессом.

Дискретность выражается в парциальном поступлении

материала

в зону аккумуляции. Механизм поступления, который

наиболее полно изучен, — мутьевые потоки.

Установленный IL Б. Вассоевичем факт ритмичного строения

разрезов

флиша в дальнейшем всеми без исключения геологами

интерпретировался как результат периодического характера фли-

шеобразующих

процессов. Иначе говоря, устанавливалось одно-

значное соответствие меязду ритмичным строением реализаций

(разрезы

флиша) и периодическим характером исходного процесса.

Однако мояшо легко показать, что такое соответствие осуще-

ствляется

далеко не всегда. Следующий отвлеченный пример

наглядно иллюстрирует эту мысль

[239].

Пусть в нашем распоряжении имеется п кубиков. Каждый

кубик условно означает

единичный

флишевыи миогослой со свой-

ственным данной свите набором пород и характерными текстурами.

Поскольку любая конкретная свита характеризуется прежде всего

постоянным и ограниченным набором пород, то перепумерация

кубиков (i = 1, п) не обязательна. Перед нами поставлена задача:

за

ограниченный отрезок времени T составить из этих кубиков

неупорядоченную последовательность (модель разреза флинта).

Очевидно, что эту задачу можно решать неоднозначно. Можно

каждый следующий кубик ставить в эту последовательность через

равные промежутки времени TIn (периодический процесс). Ту же по-

следовательность можно воспроизвести, укладывая кубики только

течение времени Т/2 с частотой Т/(2п). Возможен и такой вари-

ант, когда интервалы времени между укладкой

i-то

и i + 1-го ку-

биков сильно отличаются друг от друга (непериодический процесс).

Важно

подчеркнуть, что все три способа приводят к одной

и той же последовательности (к одному и тому же чередованию

пород в разрезе, характеризующемуся к тому же четко выражен-

ной ритмичностью). Обратную же задачу (восстановить, каким

из трех названных способов образована наблюдаемая в разрезах

флиша ритмичность) мы решить не в состоянии. Наиболее веро-

ятно, что флишепакоплеиие реализуется по схеме апериодического

процесса, как наиболее общей. По и это не более чем предполо-

жение.

При таком подходе накопление ритмов во флише можно трак-

товать

как нестационарный и неэргодический процесс, в котором

среднее по ансамблю (ритмичность) не соответствует среднему

по времени (периодичность). Таким образом, выявляемые в стро-

ении

геологических разрезов «скрытые закономерности» могут

соотноситься с характером тектонических и седиментологических

процессов только в том случае, если они получены на базе конкрет-

пой модели, постулирующей

периодический

режим исходного

процесса. В этом же смысле допустима и интерпретация «обнару-

женных»

циклов, или периодов, разного порядка.

Что

касается используемой при решении такого рода задач

терминологии, то важно, чтобы употребляемые при решении

конкретной задачи термины были строго определены. Тогда

рамках задачи они будут пониматься однозначно и не будет

возникать разночтений пи на этапе конструирования исходной

модели, ни при интерпретации полученных результатов.

Класс

же задач, /для которых определенная таким путем терми-

нология оказывается оправданной (без специальных оговорок),

расширяется по мере развития геологической теории, на которую

он опирается. Но даже в пределе, когда геологическая наука

достигнет высокой степени теоретического совершенства, можно

утверждать,

что и тогда процесс формализации

понятийной

базы

не завершится [208, 236].

Именно по этой

причине

современные дискуссии по поводу

.ГО

выяснения «истинного» смысла таких понятий, как

«цикл»,

«ритм»,

«период»

и т. п., оказываются, как правило, безрезультатными.

Не помогают ни логика, ни обращение к этимологии этих понятий,

ни

аппеляция

к историческому первоисточнику. Вопрос неизбежно

остается

открытым. Необходимость

7ке

в этих дискуссиях отпадет

сама

собой, когда за этими понятиями будет стоять конкретная

геологическая теория, позволяющая конструктивно их исполь-

зовать

для возможно более широкого класса задач, в рамках

которых могут быть получены нетривиальные результаты, не

допускающие к тому же двойственного толкования. Поэтому

единственно целесообразным, с нашей точки зрения, является

введение данных

понятий

«по определению», причем таким обра-

зом,

чтобы в рамках этих определений они не допускали двой-

ственного толкования. Такое требование можно выполнить, если

записать вводимые определения на формальном, в частности

математическом, языке, что мы и попытаемся сделать.

Пусть геологический разрез в отношении любой характери-

стики, закономерность колебания которой исследуется, предста-

вляется в виде последовательности {a,}, i •= 1, N. Последова-

тельность {а

(

} будем называть арифметизироваиным разрезом.

Тогда

интересующие нас

понятия

целесообразно определить

следующим образом.

Повторяемость.

Будем говорить, что арифметизированный

разрез

{а,-}

обладает свойством повторяемости в отношении хотя

бы одного элемента {а}, если существует такой набор целых чисел

s = l, п}, что = а.

Существенно в данном определении то, что повторяемость

определяется только в отношении отдельных признаков, характе-

ризующих разрез: повторение слоя песчаника через произвольный

интервал, максимумов гранулометрической кривой и т. д. На-

пример, последовательность

{1,

2, 5, 7, 1, 3, 4, 8, 9, 0, 1} обладает

свойством

повторяемости в отношении элемента

{1},

а последова-

тельность {1, 2, 0, 5, 6, 1, 2, 4, 3, 1, 2, 9, 1} — в отношении как

элемента

{1},

так и элементов

{1,

2}.

Ритмическая повторяемость (ритмичность). Будем говорить,

что арифметизированный разрез {a

} обладает свойством ритми-

ческой повторяемости в отношении хотя бы одного элемента {а},

если, во-первых, он обладает свойством повторяемости в отноше-

нии этого элемента, во-вторых, существует такое постоянное

число /, называемое шагом повторяемости, что

+ 1

= j

~\-

и, в-третьих, Uj Ф а, если ) Ф]

. Например, свойством ритми-

ческой повторяемости в отношении элемента {1} обладает после-

довательность

{1,

3, 5, 1, 2, 4, 1, 6, 7, 1, 8, 9}, а в отношении эле-

ментов

{1,

2} — последовательность {1, 2, 5, 6, 1, 2, 3, 4, I, 2,

7, 6, 1, 2, 8, 9}. Существенным в данном определении является то,

что из свойства ритмической повторяемости не следует, что еди-

ницей

такой повторяемости является ритм. Из приведенных нами

примеров видно, что, хотя лтежду ритмически повторяющимися

элементами {1} или

{1,

2} число других элементов постоянно

= const, сами эти элементы каждый раз различные. Поэтому

ритмически повторяющиеся элементы не могут разбивать всю

последовательность па ритмы, означающие как бы «вещественные»

единицы

ритмичности. На этом обстоятельстве вполне справедливо

настаивает

Н. Б. Вассоевич с соавторами [27, 45].

Действительно, в одной из работ указанных авторов читаем

[45,

с. 23]: «ритм не то, что повторяется, а то, как (курсив наш. —

С. Р.) повторяется, а то, что повторяется надо именовать циклом».

Правда,

получается, что у ритмично построенных разрезов еди-

ницей

ритмичности служит

цикл.

Это противоречит нашему опре-

делению ритмичности, из которого, как мы уже отметили, следует,

что ритмическая повторяемость не имеет вещественной

единицы

ритмичности, отличной от повторяющихся элементов разреза,

поскольку между

ними

включаются элементы, в общем случае

не характеризующиеся ритмической повторяемостью.

Циклическая

повторяемость

(цикличность).

Введем понятие

о разбиении арифметизированного разреза А =

{а,}

на р упоря-

доченных подмножеств вида A

= {a

s +1

, . . ., a

}, k = 1, р,

= N и U А

= А. А

будем называть циклом. Тогда разрез

будет обладать свойством

циклической

повторяемости, если

существует

такое разбиение, что, во-первых, первые Z

элементов

всех

подмножеств совпадают и, во-вторых, s

^ Z

, к = 1, р.

Примером

циклической

повторяемости является последова-

тельность вида {1, 2, 3, 4, 1, 2, 3, 1, 2, 3, 4, 1, 2, 3, 1, 2, 3,

4},

где I

= 3 и Z

= 4. В данном определении существенно

не только то, что

циклическая

повторяемость определяется с точ-

ностью до циклов, но и что в пределах каждого цикла фикси-

руется

четкий

порядок следования элементов. Число же эле-

ментов в повторяющихся циклах в общем случае может быть

различным.

Периодическая

повторяемость

(периодичность).

Арифметизи-

рованный разрез {a

} будет обладать свойством периодической

повторяемости в отношении упорядоченного набора элементов

если он обладает свойством

циклической

повторяемости при

условии, что Z

= Z

. Примером последовательности, обладающей

свойством

периодической повторяемости в отношении набора

элементов

{1,

2, 3, 4} будет последовательность вида

{1,

2, 3, 4,

1, 2, 3, 4, 1, 2, 3,

4}.

Ясно, что периодичность — наиболее жесткое

условие повторяемости, когда должны быть одновременно вы-

полнены условия ритмической и

циклической

повторяемости

Периодичность в явном виде в реальных разрезах не фиксируется.

Поэтому о периодической повторяемости имеет смысл говорить

только в том случае, если строение разреза исследуется аналити-

ческими методами. Тогда периодичность является результатом

аппроксимации числовой последовательности, которой закодиро-

ван

разрез, тем или иным аналитическим выражением, найденным,

например, с помощью методов гармонического анализа.

РИТМИЧЕСКАЯ

II ЦИКЛИЧЕСКАЯ ПОВТОРЯЕМОСТИ

ГЕОЛОГИЧЕСКИХ

ЯВЛЕНИЙ, ФИКСИРУЕМЫЕ

РАЗРЕЗАХ ОСАДОЧНЫХ ТОЛЩ

Геологи

со времен Н. А. Головкинского и И. Вальтера, т. е.

последней трети XIX в., прочно усвоили мысль, что вертикаль-

ные колебательные движения земной коры предопределяют напра-

вленное смещение фациальных зон накопления осадков, что

порождает

слоистое строение осадочных толщ. Правда, в насто-

ящее

время эта идея сохранила научную ценность только для

ограниченного числа стратифицированных осадочных образова-

ний, накапливающихся преимущественно в шельфовой зоне от-

крытых морей и реализующих слоистость осадочно-миграционного

типа (в терминологии Н. Б. Вассоевича

[38]).

Мутационная сло-

истость (ленточные глины, турбидиты и т. п.) формируется, как

известпо,

прп фиксированном положении береговой

линии,

т. е.

под влиянием преимущественно седиментологических факторов.

Однако если различные генетические типы слоистости вне

зависимости

от обстановок и условий их образования реализуются

под действием только тектонических и седиментологических (в ши-

роком

смысле) факторов, то класс процессов, приводящих к рит-

мичности и цикличности в строении разрезов осадочных толщ,

значительно шире и интерпретация условий возникновения за-

кономерной повторяемости определенной группы пород в разрезе

во

многом зависит от формационной принадлежности исследуемой

толщи и характера (масштаба) выделенной цикличности.

настоящее время более или менее однозначное толкование

получила цикличность тех осадочных толщ, в которых, с одной

стороны,

она проявлена с максимальной отчетливостью, а с дру-

гой — в значительной мере определяет и генезис самих осадочных

образований,

по поводу которого у геологов нет серьезных разно-

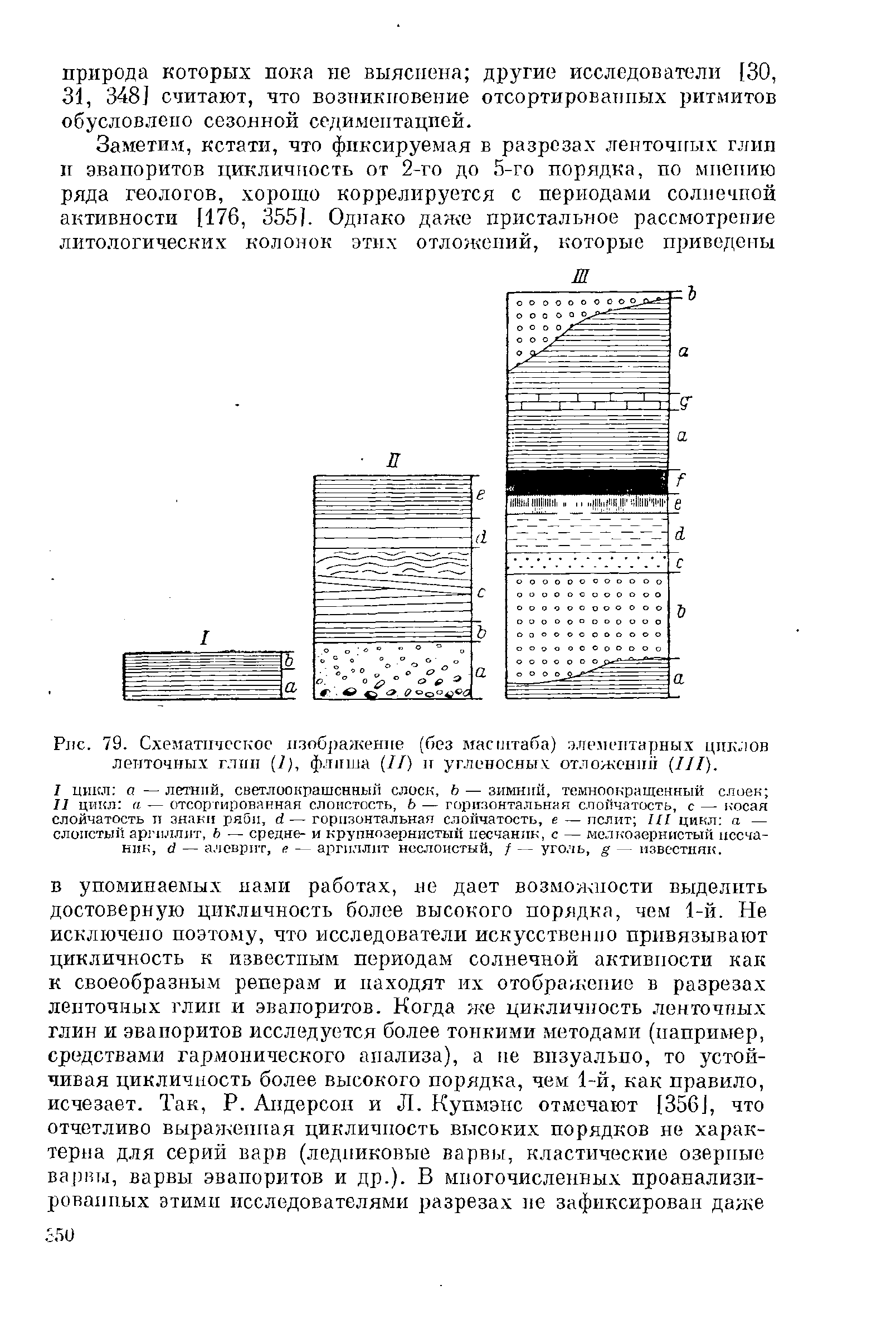
гласий. С этих позиций целесообразно выделить цикличность

озерных ленточных глин, а также флишевой и угленосной форма-

ций (рис. 79). Эти группы отложений выбраны не столько потому,

что они наилучшим образом иллюстрируют различные проявления

ритмичной и

цикличной

повторяемости в строении геологических

разрезов,

что само по себе немаловажно, сколько по

причине

принципиально разного толкования природы этой повторяемости,

фиксируемой в указанных образованиях.

Ленточная слоистость формируется в спокойной гидродинами-

ческой обстановке. В течение года накапливаются два слойка,

которые в совокупности образуют элементарный

цикл

(варв).

Таким

образом, циклическая повторяемость ленточных глин

обязана

чисто климатическим причинам — смене времен года,

которая фиксируется в виде светлоокрашенного (летнего) слойка

и темноокрашенного (зимнего). Некоторые геологи [355, 3561

выделяют

ленточные циклы более высоких порядков, связывая их

длиннопериодическими колебаниями климата (до 10—30 тыс. лет),

природа которых пока не выяснена; другие исследователи [30,

31,

348] считают, что возникновение отсортированных ритмитов

обусловлено сезонной седиментацией.

Заметил!, кстати, что фиксируемая в разрезах ленточных глин

и эвапоритов цикличность от 2-го до 5-го порядка, по мнению

ряда геологов, хороню коррелируется с периодами солнечной

активности [176, 355]. Однако даже пристальное рассмотрение

литологических колонок этих отложений, которые приведены

Рис. 79. Схематическое изображение (без

масштаба)

элементарных циклов

ленточных глин (I), фллша (ТУ) и угленосных отложении

(III).

цикл:

а —

летний, светлоокрашенный слоек,

b —

зимний, темноокращенный слоек;

II цикл:

а —

отсортированная слоистость,

Ь —

горизонтальная слойчатость,

с —

косая

слойчатость

знаки

ряби,

d —

горизонтальная слойчатость,

е —

пелит;

III

цикл:

а —

слоистый аргиллит,

Ь —

средне-

крупнозернистый песчаник,

с —

мелкозернистый песча-

ник,

d —

алеврит,

е. —

аргиллит неслоистый,

/ —

уголь,

g —

известняк.

упоминаемых нами работах, не дает возможности выделить

достоверную цикличность более высокого порядка, чем 1-й. Не

исключено поэтому, что исследователи искусственно привязывают

цикличность к известным периодам солнечной активности как

к своеобразным реперам и находят их отображение в разрезах

ленточных глин и эвапоритов. Когда же цикличность ленточных

глин и эвапоритов исследуется более тонкими методами (например,

средствами гармонического анализа), а не визуально, то устой-

чивая цикличность более высокого порядка, чем 1-й, как правило,

исчезает. Так, Р. Андерсон и Л. Купмэнс отмечают

[356],

что

отчетливо выраженная цикличность высоких порядков не харак-

терна для серий варв (ледниковые

варвы,

пластические озерные

варвы,

варвы эвапоритов и др.)- В многочисленных проанализи-

рованных этими исследователями разрезах не зафиксирован даяче