Равич-Щербо И.В. Психогенетика

Подождите немного. Документ загружается.

значения пробанда по исследуемому признаку на коэффициент род-

ства; А

—

константа регрессионного уравнения.

Решение этих уравнений позволяет оценить следующие парамет-

ры: В

, представляет собой показатель среднего сходства между МЗ и

ДЗ близнецами;

—

оценку удвоенной разницы между средними в

группах МЗ и ДЗ близнецов (с учетом ковариации между значениями

МЗ и ДЗ пробандов); В

оценивает долю дисперсии, объясняемую сре-

довыми влияниями, общими для членов близнецовой пары

или С

); В

, отражает разницу h

- h

, где h

— коэффициент наследу-

емости в широком смысле и h

— коэффициент наследуемости в оп-

ределенной группе (например, коэффициенты наследуемости IQ в

группах здоровых людей и людей, страдающих ФКУ, отличаются друг

от друга; В

показывает разницу коэффициентов наследуемости, по-

лученных в генеральной популяции и специфической выборке); и,

наконец, В

оценивает коэффициент наследуемости (h

), т. е. показа-

тель того, насколько индивидуальные различия в исследуемой выбор-

ке объясняются наследуемыми влияниями.

Интересной особенностью ДФ-метода является то, что он позво-

ляет тестировать гипотезу о сходстве или различии этиологии нор-

мально распределенных и экстремальных значений. Сравнение рег-

рессионных коэффициентов

позволяет проверить гипотезу о

том, сходны ли этиологии девиантных и «средних» значений, напри-

мер, по тесту на математические способности. Если этиология неспо-

собности к математике отличается от этиологии средних математи-

ческих способностей, то

и В

должны статистически надежно отли-

чаться друг от друга. Если же дети, которые имеют трудности в

овладении математикой, представляют собой не отдельную группу, а

край нормального распределения, то

статистически отличать-

ся друг от друга не должны,

Разные формулы для вычисления коэффициентов наследуемости

характеризуются разного рода допущениями и ограничениями. В не-

скольких исследованиях было продемонстрировано, что применение

разных формул на одном и том же эмпирическом материале дает раз-

ные результаты. Поэтому интерпретация данных, полученных одним

методом близнецов, должна проводиться с учетом всех ограничений,

свойственных этому методу. Ф. Фогель и А. Мотульски [159] отмечают,

что даже при сильно упрощающих допущениях (например, отсутствия

ассортативности, доминирования и т.д.) все равно остаются система-

тические ошибки, которые невозможно полностью проконтролиро-

вать. Они рекомендуют вычислять из одних и тех же эмпирических

данных альтернативные оценки и сравнивать, насколько хорошо они

совпадают.

Метод приемных детей.

При допущении, что среда семей-усыно-

вителей не коррелирует со средой тех биологических семей, из кото-

рых данные дети усыновляются, корреляции детей с их биологичес-

201

кими родителями представляют собой «чистые» генетические корре-

ляции (т.е. прямую оценку h

или

а с родителями-усыновите-

лями — «чистые» средовые корреляции (с

или V

Однако в том

случае, если среды биологических и приемных семей похожи, допу-

щение о «чистоте» полученных оценок генетической и средовой со-

ставляющих чаще всего неправомерно (по крайней мере в тех случа-

ях, когда корреляция сред неизвестна). Методологически адекватным,

хотя практически и не всегда возможным решением в подобной ситу-

ации служит получение нескольких оценок генетического и средово-

го компонентов при разных значениях корреляции сред.

Таким образом, главной причиной беспокойства при использова-

нии метода приемных детей является допущение об отсутствии кор-

реляции между биологическими и приемными семьями. Кроме того,

исследователи должны убедиться в том, что семьи-усыновители реп-

резентативны общей популяции, т.е. не отличаются от среднепопуля-

ционной семьи по уровню благосостояния, образования и т.п. Если

семьи-усыновители нерепрезентативны, закономерности, полученные

в результате их анализа, не могут считаться справедливыми для гене-

ральной популяции.

АНАЛИЗ ПУТЕЙ

Приведенная выше логика разложения фенотипической диспер-

сии на ее составляющие, реализованная в нескольких эмпирических

методах, представляет собой один из способов определения коэффи-

циента наследуемости того или иного признака. Но понятие наследу-

емости можно также проанализировать при помощи «анализа путей».

Анализ путей в последние десятилетия широко используется и в

психогенетике, и в науках о поведении вообще. Он был предложен

генетиком С, Райтом еще в 30-х годах и затем им же и другими иссле-

дователями детально разработан. Четкое изложение его основ и пра-

вил использования содержится в упоминавшемся труде М. Нила и

Л. Кардона [342], которые характеризуют этот метод следующим

образом.

Диаграмма путей — эвристичный способ наглядного графическо-

го представления причинных и корреляционных связей (путей) меж-

ду переменными, позволяющий дать полное математическое описа-

ние линейной модели, которую применяют исследователи. Тем са-

мым диаграмма путей способствует ее пониманию, верификации или

представлению результатов. В целом путевые модели — «экстремально

обобщенный» способ анализа, один из многих мультивариативных

методов (к ним же относятся методы множественной регрессии, фак-

торный и дискриминантный анализы и т.д.).

Существуют определенные правила построения диаграмм пу-

тей (рис. 8.4). Прямоугольники (или квадраты) обозначают наблюда-

202

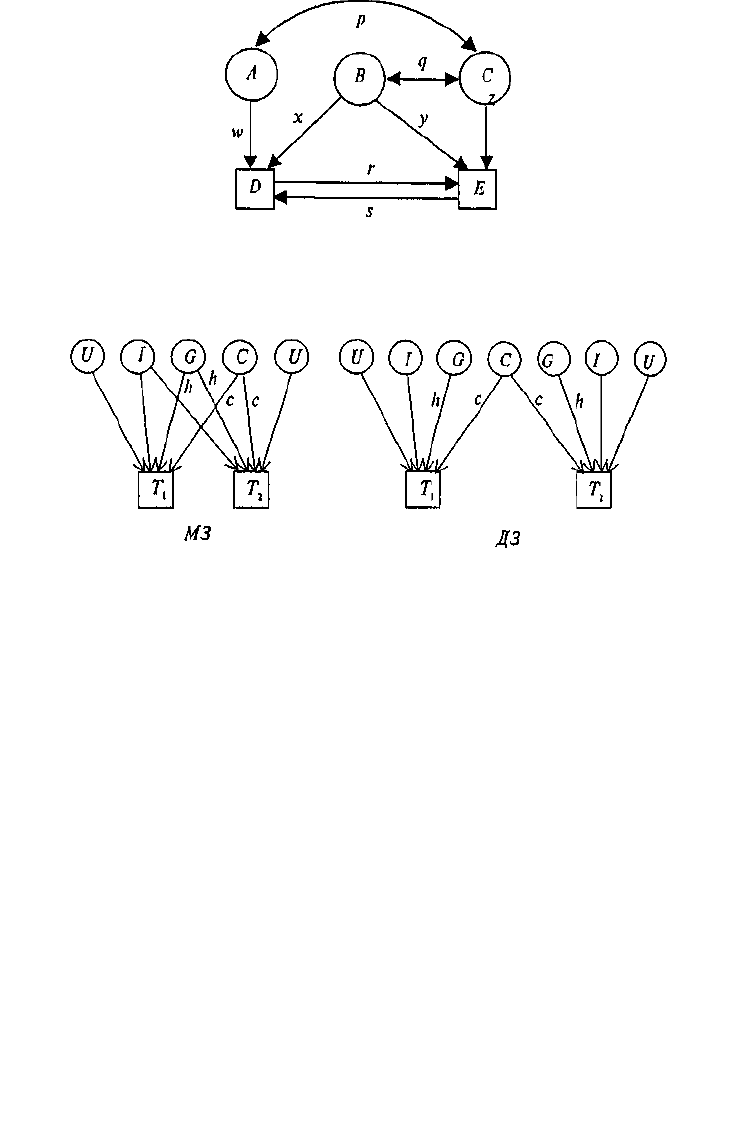
Рис. 8.4.

Диаграмма путей, объединяющая три латентных

(А, В, С)

и две

наблюдаемых

и Е) переменных.

q —

корреляции; r, s,

w, х, у, z

— путевые коэффициенты.

Рис. 8.5.

Диаграмма путей для корреляций совместно живущих пар

МЗ

ДЗ

близнецов.

— близнецы одной пары.

G —

генотип;

С—

общая среда;

U —

индивидуаль-

ная (уникальная) среда; I— эпистаз. Пути h,

с —

влияния

G, С

на исследуемую

черту.

емые переменные; круги (или эллипсы) — латентные, неизмеряе-

мые переменные (на рис. 8.4.

Е; А, В,

С соответственно).

Связи между переменными обозначаются стрелками: постулиро-

ванные исследователем причинно-следственные — направленной в

одну сторону («путь» от причины к следствию); наблюдаемые ассо-

циации — двусторонней. На рис. 8.4 первые —

w, x, у, z, r, s

(путевые

коэффициенты); вторые —

(коэффициенты корреляции). Ина-

че говоря, модель выделяет зависимые переменные

Е),

подле-

жащие объяснению или прогнозированию, и независимые

(А, В, С),

действие которых должно объяснить или предсказать зависимые пе-

ременные и их связи. Есть и другие, более детальные, правила офор-

мления и чтения путевых диаграмм, но мы их рассматривать не будем.

На рис. 8.5 даны модели путей для корреляций совместно живу-

щих пар МЗ и ДЗ близнецов по экстраверсии, из которых следует, что

203

корреляция МЗ близнецов

может быть выражена через сумму

путей, связывающих их, т.е.

и сс

;

иначе говоря, r

МЗ

= h

+с

. Для ДЗ

это будут пути h х 1/2 х h и cc

т.е. r

ДЗ

= 1/2 h

+ с

. Вычитая, получим

МЗ

— r

ДЗ

= h

+ с

— 1/2 h

— с

= 1/2 h

; чтобы получить полную генетичес-

кую дисперсию (а не половину ее), удваиваем разность корреляций

= 2(r

MЗ

— r

ДЗ

)

и получаем описанный выше коэффициент наследу-

емости, справедливый для близнецовых исследований. Аналогичным

образом могут быть построены путевые диаграммы для семейных и

любых других данных.

Единицы измерения, используемые в анализе путей, отличаются

от тех, которыми мы оперировали тогда, когда рассматривали по-

нятие наследуемости на примере разложения фенотипической дис-

персии. Если при разложении дисперсии мы пользовались квадратич-

ными единицами (например, h

, V

то в данном случае наследуе-

мость описывается на языке стандартных отклонений. Тогда путевые

коэффициенты являются коэффициентами регрессии, полученными

для переменных не в исходных единицах, а для стандартизованных

переменных.

Несмотря на широкое использование этого метода и его достоин-

ства, которые заключаются прежде всего в наглядной демонстрации

представлений о компонентах, влияющих на исследуемый признак,

он имеет и своих критиков. Так, Ф. Фогель и А. Мотульски «не уверены

в том, что этот метод биометрического анализа внесет существенный

вклад в наше понимание генетических факторов» [159]. Одно из глав-

ных сомнений вызывает тот факт, что в диаграмму путей и, следова-

тельно, в дальнейший математический анализ закладываются уже

имеющиеся у исследователя предположения о влияющих на признак

факторах, их причинно-следственных отношениях и т.д., и результат

анализа зависит, таким образом, от корректности заранее имеющих-

ся исходных позиций.

АНАЛИЗ МНОЖЕСТВЕННЫХ ПЕРЕМЕННЫХ

До сих пор наши рассуждения концентрировались в основном на

одном фенотипе, т.е. нашей конечной переменной являлся какой-то

конкретно взятый фенотип. А если мы заинтересованы в одновремен-

ном изучении двух фенотипов, которые теоретически могут быть свя-

заны между собой? Например, связана ли вариативность в популяции

по таким высоко коррелирующим признакам, как вербальный и не-

вербальный интеллект? Насколько вероятно предположение о том,

что вариативность по этим двум признакам может быть объяснена

действием одних и тех же генетических и средовых влияний? Иными

словами, если два признака коррелируют на фенотипическом уровне,

то эта корреляция может быть результатом действия как генетичес-

204

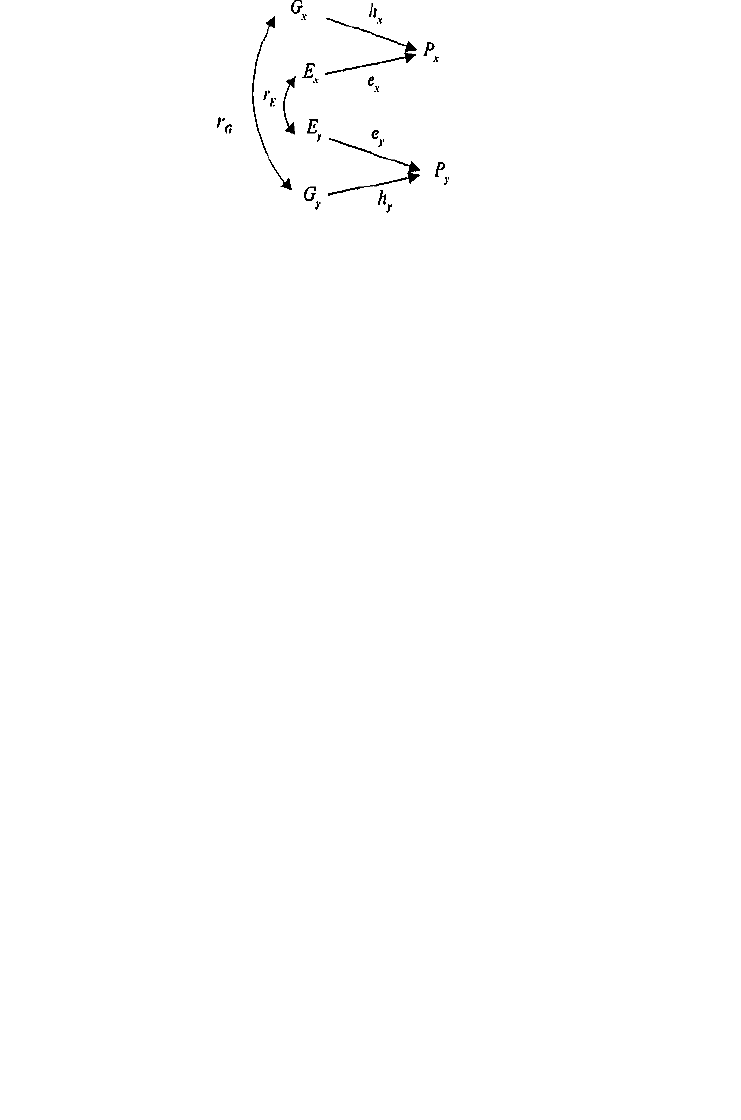
Рис. 8.6.

Диаграмма путей фенотипической корреляции двух призна-

ков

демонстрирующая роль генетической r

и средовой r

со-

ставляющих.

ких, так и средовых факторов, и задача может заключаться в том,

чтобы понять происхождение не только самих фенотипов, но и их

корреляции.

Среди генетических причин, которые могут привести к появлению корре-

ляции между признаками на фенотипическом уровне, следует указать на так

называемый эффект

плейотропии,

или множественного влияния одних и тех

же генов на разные признаки. Кроме того, различные популяционные про-

цессы, например неслучайное скрещивание и смешивание популяций, также

могут привести к возникновению корреляции между фенотипами.

Примером средового влияния на формирование фенотипической корре-

ляции может служить дефицит питания: недоедающие дети обычно значи-

тельно ниже своих сверстников как по весу, так и по росту, т.е. связь этих двух

характеристик обеспечивается одним средовым фактором.

Значимость такого рода одновременного моделирования множе-

ственных переменных трудно переоценить. Существуют целые классы

поведенческих признаков, которые высоко коррелируют между собой

(например, различные показатели когнитивной сферы, показатели

эмоционально-волевой сферы и т.п.). Предположение о том, что ва-

риативность по высоко коррелирующим психологическим признакам

может объясняться действием одних и тех же генетических и/или сре-

довых факторов кажется весьма правдоподобным.

Математическое описание множественных моделей достаточно

просто, Рис. 8.6 представляет собой иллюстрацию того, как модель

путей, рассмотренная нами, может быть разработана для одновре-

менного анализа двух коррелирующих признаков. Подобно тому как

фенотипическая вариативность отдельно взятого признака

(Р

)

отра-

жает вариативность генотипов

)

и сред (e

), фенотипическая кор-

реляция между

Y (rР

)

может быть результатом набора генети-

ческих (h

) и средовых

(е

)

путей, где r

и r

представляют

205

собой генетическую и средовую корреляции, соответственно. В ре-

зультате

+ е

ОЦЕНКА СОСТАВЛЯЮЩИХ ФЕНОТИПИЧЕСКОЙ ДИСПЕРСИИ

МЕТОДОМ ПЕРЕБОРА (ПОДБОРА) МОДЕЛЕЙ (МПМ)

Некоторые корреляции родственников (например, корреляции МЗ

близнецов, разлученных при рождении, или приемных сиблингов —

усыновленных детей-неродственников, выросших в одном доме) сами

по себе дают информацию, которой достаточно для получения отве-

тов на центральные вопросы психогенетики о том, насколько вариа-

тивность данного признака объясняется разнообразием сред и гено-

типов, наблюдаемых в данной популяции. Подобное может быть сказано

и о тех методах психогенетики, которые сопоставляют корреляции,

полученные у двух типов родственников, например корреляции МЗ и

ДЗ близнецов, приемных детей — с биологическими и приемными

семьями.

Однако в современных исследованиях предпочтение при анализе

психогенетических данных отдается не прямым оценкам составляю-

щих фенотипической дисперсии, а применению метода перебора

(подбора) моделей. Этот метод представляет собой специфическую

адаптацию метода структурного моделирования к задачам генетики

количественных признаков. МПМ отличается несколькими преиму-

ществами: 1) более точной оценкой искомых параметров; 2) воз-

можностью оценивать более сложные генетические модели, напри-

мер учитывать половые различия и моделировать ГС-корреляции и в-

заимодействия; 3) возможностью сводить в одном анализе данные,

относящиеся к разным типам родственников, и получать, благодаря

этому, относительно несмещенные оценки параметров и 4) возмож-

ностью тестирования нескольких альтернативных моделей с целью

выбора той, которая наилучшим образом соответствует исходным дан-

ным.

В рамках генетики количественных признаков применение метода

перебора моделей сводится к решению систем уравнений для обна-

ружения такого набора параметров (т.е. подбора такой модели), ко-

торый наилучшим образом соответствует набору исходных данных

(корреляций родственников). Главное преимущество МПМ заклю-

чается в том, что он позволяет тестировать все те допущения,

которые не учитываются в традиционных методах генетики коли-

чественных признаков. Например, обсуждая метод близнецов, мы

указывали на то, что одним из допущений этого метода является

допущение об отсутствии ассортативности. МПМ позволяет срав-

нить две модели (учитывающую ассортативность и не учитываю-

206

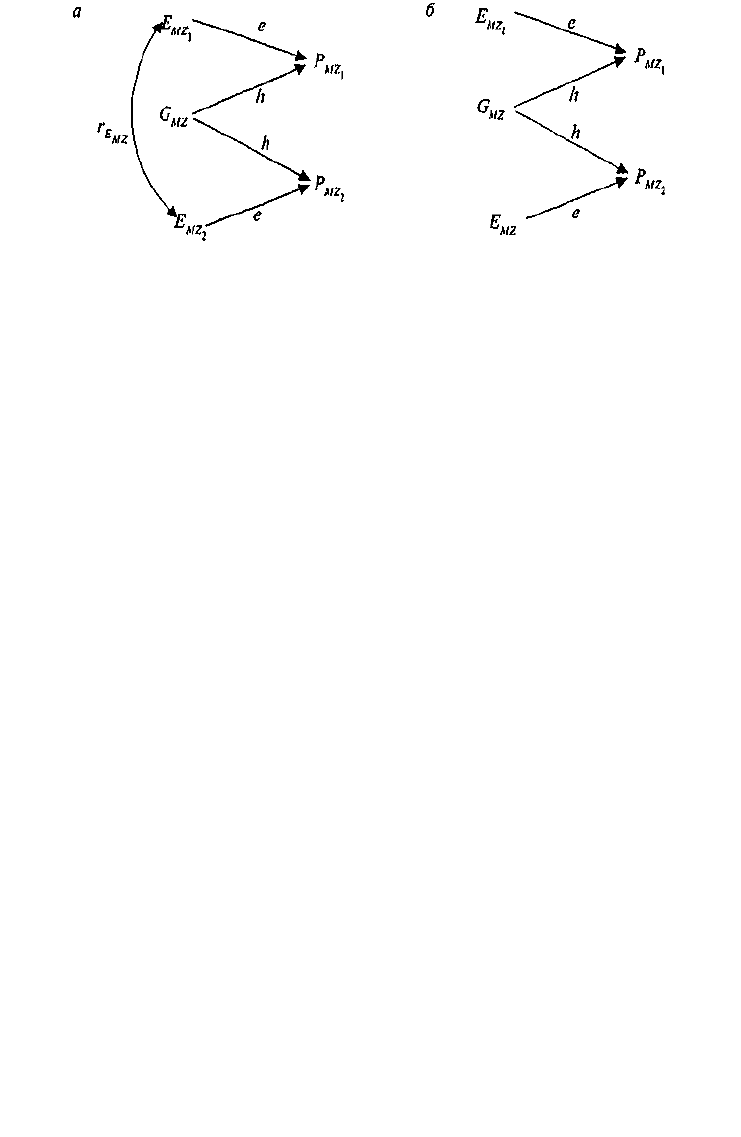
Рис. 8.7.

Диаграмма путей фенотипических корреляций по исследуемому

признаку для двух типов МЗ близнецов:

(а)

выросших вместе и

(6)

разлу-

ченных при рождении [по: 364].

Обозначения — в тексте.

щую ее) и выбрать ту, которая наилучшим образом соответствует

эмпирическим данным.

В качестве еще одного примера применения МПМ рассмотрим

анализ родственных корреляций на основе модели, приведенной

на рис. 8.7. Эта модель описывает фенотипическое сходство МЗ двух

типов — выросших вместе

(а)

и разлученных при рождении

(б).

Каждая из моделей содержит: две измеряемых переменных — фе-

нотипические значения близнецов,

MZ1

МZ2

и две латентных,

неизмеряемых переменных — эффекты генотипа

(G),

и эффекты сре-

ды

(Е).

Среды близнецов, выросших вместе, коррелируют

E MZ

Путь

от латентной переменной — генотипа

(G)

к измеряемой перемен-

ной — фенотипу

(Р)

обозначается h; путь от латентной переменной

среды

(Е) к

измеряемой переменной фенотипа

(Р)

обозначается

е.

Задача моделирования заключается в том, чтобы решить систему

уравнений и оценить два неизвестных параметра —

и h. Применяя

правила анализа путей, запишем следующую систему уравнений:

.)(

;)(

hhhrб

erheerhra

EMZEMZMZ

=×=

+=⋅⋅⋅=

Эта система содержит два уравнения и два неизвестных и решает-

ся алгебраически.

Итак, мы проиллюстрировали простое приложение МПМ. На пер-

вом этапе с помощью диаграмм путей записывается система уравне-

ний, описывающих фенотипические корреляции для всех типов род-

ственников, данные которых анализируются. Затем исследователь фор-

мулирует набор альтернативных моделей, среди которых и ведется

поиск модели с наилучшим соответствием эмпирическим данным.

207

Например, исследователь может протестировать соответствие полу-

ченным данным следующих трех моделей, согласно которым феноти-

пическое сходство родственников по определенному признаку объяс-

няется: 1) только аддитивной генетической составляющей; 2) только

доминантной генетической составляющей; 3) наличием и аддитив-

ной, и доминантной генетических составляющих. Модель наилучшего

соответствия выбирается на основе значения χ-квадрата и других ста-

тистических показателей, оценивающих степени соответствия модели

исходным данным.

Как уже указывалось, перебираемые модели могут быть очень раз-

ветвленными и сложными; они могут включать в себя множественные

фенотипы, измеренные у нескольких типов родственников лонгитюд-

ным методом (т.е. несколько раз за время исследования) и т.д.

Результаты применения МПМ могут быть использованы только

при тестировании альтернативных моделей. Иными словами, МПМ

не дает «доказательств» правильности тестируемой научной гипоте-

зы; он позволяет лишь выбрать наиболее адекватную материалу гене-

тическую модель. МПМ является элегантным и сложным статисти-

ческим методом, применение которого требует наличия определен-

ных навыков*.

СТРУКТУРНОЕ МОДЕЛИРОВАНИЕ

Структурное моделирование —сложный современный метод, требующий

и больших объемов выборок, и специальной квалификации исследователя, и

наличия соответствующих компьютерных программ. Детальное изложение его

не входит в задачи данного учебника, мы даем краткую характеристику его

возможностей, чтобы читатель, столкнувшись в литературе с этим типом ана-

лиза, смог адекватно понять его смысл.

Статистические методы моделирования с помощью линейных структур-

ных уравнений (МЛСУ)**, описывающих латентные переменные, были разра-

ботаны на основе приемов статистического анализа множественных пере-

менных, используемых биологами, экономистами, психологами и социолога-

ми, МЛСУ предполагает формулирование набора гипотез о влиянии одних

переменных (независимых) на другие (зависимые) переменные. Соответствие

подобного набора гипотез, т.е. теоретической модели, и реальных данных,

собранных при работе с конкретной выборкой, т.е. эмпирической модели,

формализуется с помощью статистического алгоритма, оценивающего сте-

пень их согласованности (меру соответствия).

* Полное описание спецификации МПМ в рамках количественной генети-

ки выходит за пределы данного учебника. Подробное изложение этого метода да-

ется в руководствах Лоэлина [320J, а также Нила и Кардона 1342]. На русском

языке пример применения МПМ в рамках психогенетики приведен в работе

Е.А. Григоренко и М. ЛаБуды 144].

** История возникновения и этапы детальной разработки МЛСУ описаны

Бентлером [189; 190], а в работах Боллена [198] и Бентлера и его коллег [191]

содержится современное техническое описание МЛСУ.

208

МЛСУ особенно полезно при статистическом анализе большого количе-

ства переменных, интеркорреляции которых известны. Задачами его являют-

ся: суммирование этих переменных, определение отношений между ними, оцен-

ка качества измерительных инструментов, контроль ошибки измерения (как

для измеряемых, так и для латентных переменных) и нахождение соответ-

ствия между измеряемыми и латентными структурами. Правомерно будет

сказать, что в ситуациях, когда набор переменных неточно измеряет латент-

ную структуру, являющуюся предметом исследования, т.е. практически в лю-

бом случае, когда больше чем одна наблюдаемая переменная используется

для представления латентной структуры, МЛСУ с латентными переменными

следует применять как наиболее адекватный метод статистического анали-

за. Учитывая, что в психологии большинство латентных структур измеряется

именно посредством не одной, а нескольких переменных и не может быть

представлено без ошибки измерения, возможность и необходимость приме-

нения МЛСУ в этой области знаний становится очевидной.

Моделирование с помощью структурных уравнений представляет собой

метод, родственный методу систем регрессионных уравнений, который ис-

пользуется при формулировании, детализации и тестировании теории или

гипотезы. Структурные уравнения соотносят зависимые переменные и на-

бор детерминирующих (независимых) переменных, которые в свою очередь

могут выступать в роли зависимых переменных в других уравнениях. Подоб-

ные линейные уравнения в совокупности с уравнениями, детализирующими

компоненты дисперсии и ковариации независимых переменных, составляют

структурную модель. Составление и запись уравнений, детализирующих ком-

поненты дисперсии и ковариации независимых переменных, осуществляют-

ся с помощью матричной алгебры.

Статистической основой МЛСУ является асимптотическая теория, подра-

зумевающая, что оценка и тестирование моделей осуществляются при нали-

чии относительно больших по численности выборок испытуемых. Использо-

вание МЛСУ требует больших затрат компьютерного времени, поэтому пользо-

ватели при тестировании моделей предпочитают использовать стандартные

статистические пакеты типа LISREL [295] и EQS [189]. Эти пакеты, несмотря

на различия в деталях, основаны на одних и тех же общих математических и

статистических подходах, применяемых к анализу систем линейных структур-

ных уравнений. Основополагающая математическая модель [189] относится

к классу ковариационных структурных моделей, включающих как множествен-

ную регрессию, анализ путей, одновременный анализ уравнений, конфирма-

торный факторный анализ, так и анализ структурных отношений между латен-

тными переменными. Согласно модели Бентлера-Викса, параметры любой

структурной модели могут быть представлены в виде регрессионных коэф-

фициентов, дисперсий и ковариации независимых переменных. Статистичес-

кая теория позволяет оценивать эти параметры с использованием мульти-

факторной нормальной теории, а также более общих теорий — эллиптичес-

кой и арбитрального распределения, основываясь на обобщенном методе

наименьших квадратов или теории минимального χ-квадрата.

* * *

В данной главе мы рассмотрели несколько краеугольных понятий

генетики количественных признаков. Ее центральным допущением

является представление о том, что фенотипическая вариативность

признака может быть представлена в виде независимо действующих

14-1432

209

генетической (аддитивной, доминантной и эпистатической) и средо-

вой (общей и индивидуальной) составляющих и составляющей, опи-

сывающей взаимодействия между генами и средой (ГС-корреляции и

ГС-взаимодействия). На этом строятся существующие в количествен-

ной генетике математические методы. Используя принцип разложе-

ния фенотипической дисперсии, можно определить так называемый

коэффициент наследуемости, который говорит о том, какой процент

фенотипической дисперсии объясняется вариативностью генотипа в

популяции, Коэффициент наследуемости может быть определен не-

сколькими способами, каждый из которых имеет свои достоинства и

недостатки, поэтому использование того или иного способа должно

определяться задачами работы, типом и объемом эмпирического ма-

териала. Одновременно генетико-математические методы позволяют

надежно выделить доли дисперсии, определяемые различиями в об-

щесемейной и индивидуальной среде. Надо лишь иметь в виду, что

содержательный анализ любого средового компонента требует при-

влечения собственно психологических знаний и иногда специального

подбора экспериментальных групп.