Raabe J. Hydro power - the design, use, and function of hydromechanical, hydraulic, and electrical еquipment
Подождите немного. Документ загружается.

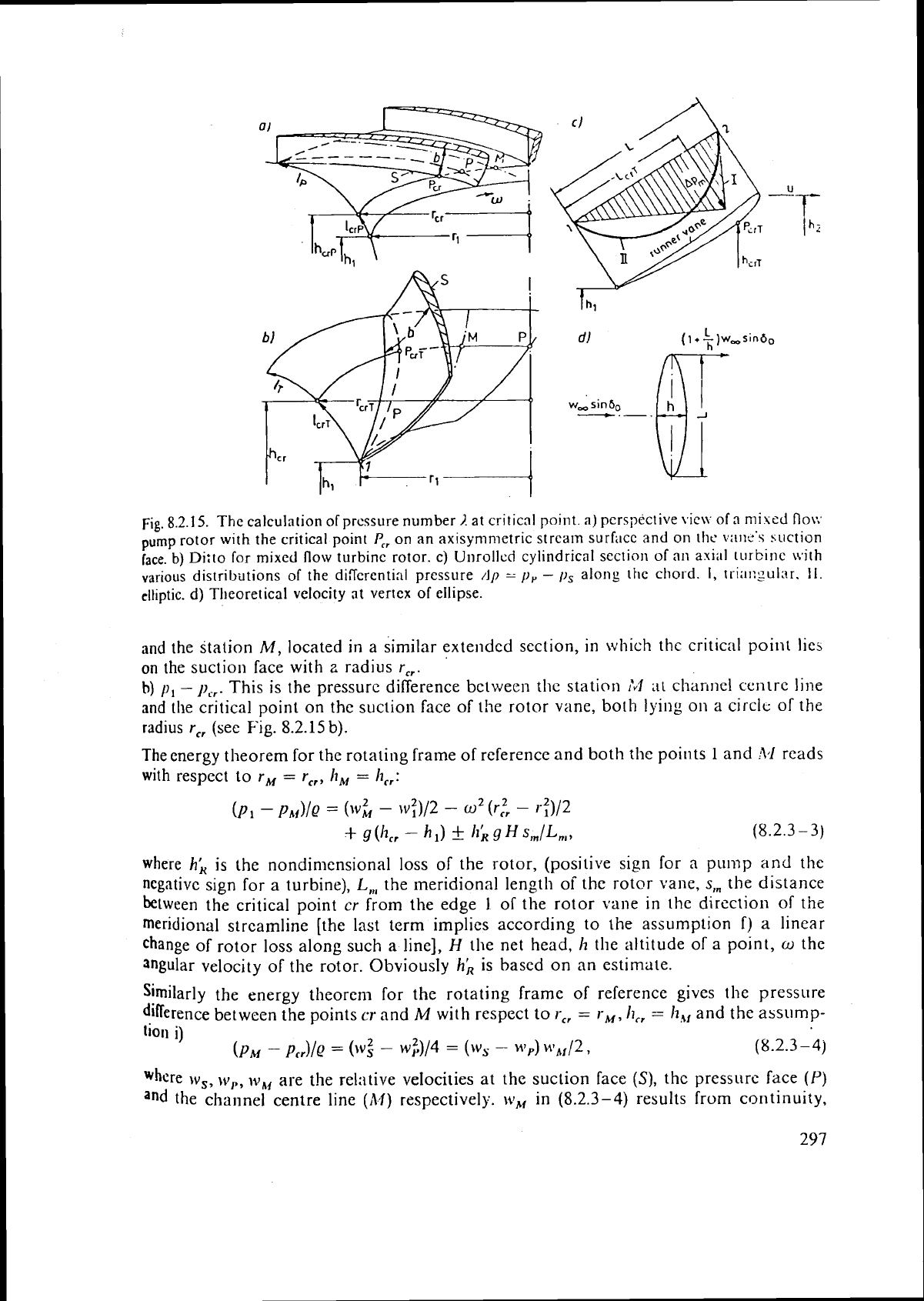
Fig.
8.2.1
5.
The calculation of prcssure number
I.
at
critical point.
a)
pcrspective
\,ic\v
of
n
nii~cd
Roc
pump
rotor
with
the critical point
PC,
on
an
axisymn~etric stream surfi~c~ and on
tht.
v;~rle's
suction
face.
b)
Di:to for mixed flow turbine rotor. c) Ui~rollcd cylindrical section of
an
axial
turbine
tvith
various
distribiltions of
the
diflerentinl pressure
/1p
-
p,
-
p,
along
the
chord.
I,
tria~:gul:tr.
11.
elliptic.
d)
Theoretical velocity
at
vertex of ellipse.
and
the station
M,
located in a similar extended section, in which thc critical point lies
on
the suction face with
z
radius r,,.
'
b)
p1
-I),,.
This is the pressure difference between the station
1'4
at channel centre line
and
the critical point on the suction face of the rotor vane, both lying on a circle of the
radius r,, (see
Fig.
8.2.15
b).
Thecnergy theorem for the rotating frame of reference and both tlie points
1
and
:!.I
reads
with respect to r,
=
r,,,
It,
=
h,,:
where
hi
is the nondimensional loss of the rotor, (positive sign for
a
pimp
and
the
ncgntivc sign for a turbine),
L,,,
the meridional length of the rotor vane,
s,,
the distance
between the critical point
cr from the edge
I
of the rotor vane
in
the
direction
of the
meridiol~al streamline [the last term implies according to the assumption
f)
a
linear
change
of rotor loss along such
a
line],
H
the net head,
h
tlie altitude of a point,
o
the
angular velocity of
the rotor. Obviously
hk
is based on an estimate.
Similarly the energy theorem for the rotating frame of reference gives the pressure
difference between the points cr and
M
with respect to
I-,,
=
r,,
I?,,
=
h,
and the
assump-
ti011
i)
(P,
-
P,,)/@
=
(1~;
-
~314
=
(kvs
-
M'~) ~'~~/2,
(8.2.3
-4)
where
lv,,
1vP,
w*,
are the relative velocities at the suction face
(S),
the pressure face
(I-')
and the ci.lanneI centre line
(,\.sf)
respectively.
w,
in (8.2.3-4) results from continuity,

applica-l
13
;in
clcnierl t.~ry turhinc ivith loc;ll il~c;~tltl~
(span)
h,
local co~it~.;\ctio~~ ~~clTi~i~~~
(1).
and tllc s~l;~iion
fro111
tllc vclr~city tri;iliglc.
I\.,,,
=
\v
sin
11,
by
ivhcrc thc val~rcs with :hc subscript c-r arc due to tllc critical poirlt.
-I'hc liclocity Jiffcrencc
\cs
-
~v,,
in
(8.2.3-3)
fc~llows from the cipplicntion
of
Stokes*
i
hcoses~i
to
thc
cIcln~~tt;isy
p~i~~;iIIcl~~gs;~rn-likc
I)ou;~dary
(scc
Fig.
5.2.2
a)
in lllc slream
surface of the rotor.
It
is fi)rn~ctl by arcs of acijaccnt prlrnllel circles, that extend from
a
strcarnlinc clcmtnt clohc to tile suction klse of tl~c rotor
vane
to
;III
elenicnt closc to the
prcssuru fr~cc.. P11t.s~ htreamli~ie elct~iients arc
:~t
the
displncemcnt thickness of the
bound,
;
arq'
layer from the vane Llcc. -Pl;us the arc of thc p:lrailcl circle is
:!
pitch multiplied with
a
contractioli f.~ctor
(P
that accounts for thc obstruction of the
flow
by
thc
boundary
:.
1:ijt:rs
and
b~
the vane.
Stokes'
theorem
(Cap.
5.2.2)
gives with respcct to the assumptions
11)
!O
C)
2
n
7
-
2
(w,
r
4')
\s,
-
\\.,
=
sin
/I
cos
11
(1,
@r.
$.
a~
svherc
r
is
the
1-o:or
\.;\nc i~iirnber,
~v,,
the pitch-a\,erageii whir! component of the relati
vclocit!.
:ir!ci
thc +-sign and --sign for turbine ancl
pump
rcspcctively.
The folloi\.ir~~ relri tion
holds
t
ri~c between
\v,,
and the pi tcll-averaged tneridional comp
nent of the rclativs velocity
N~,,,:
w,
=
nv,,
cot
/I.
Hence
i
t
I.
(1))
-
?
(\t-,,,
cot
[j
r
(D)
(?\v,
@
dfi
-
-.
-
-
.
.
-
-
--
- -
).(p cot
p--
-
-
i
I.
c'r
21.
sin2
,!I
ar
a@
+
\\.,,,COt
/3@
+
\I.,,,
cot
/,'r-.
at-
i~!scrtinz this
in
(8.2.3
-
6)
yieltls
2
n
2
n
-
-
-
-
I\.,
-
\\.,
=
--
@
2
or
sin
p
cos
ri
+
--
sin
/?
co
3
w,,,
+
r~Pcotp--
+
w,,I-cotp7
.
21.
.
;@I
CI'
According to acsum~tion h) thcse pnrtia! derivatives
in
t~
first order approximation
bc
obtained l'rom tile vr~!ues
/I,,
/jl,
w,,,,,
I\*,,,
at
stations with ri~ditis
r,
and
r,.
respecti
\vhich
arc know~i from tile velocity trianzles of the ele~nelitary turbines c
from
the coiltraction coefficients
0,
and
@,, which have to be estimated forth
Thus
FB
2,
b)
--
dwln
Wrn~
-
I'm
I
3)
7
=
---
-
c)
--
=
--
(
'r r2
-
rl
dr
r2
-
rl
Inserting
(8.2.3
--
9)
i11
(8.2.3-S),
this and
w,,
from
(8.2.3-5)
in
(8.2.3-4),
and
then
(8.2
nrld
(8.2.3--4)
in
(5.2.3-2),
and
this
in
(8.2.3-
1)
yields with respect to the assum
d)
by
which
\cl
=
11,
:cos
/I,
and
c,,
=
0,
298

ds,
sin
/I,
r,
h,
)
-
-
(QCr
sin
pCr
re,
)
1
-
[(
-
I]
cos2
/il
Ilk
S,
r2
cos
/IZ
+
-+
-----
--------
(";
L,,, )(t+,Kl12
\~llll
cr
P2
-
fi
1
cot
p,,
--
--
tv,
sin2!,,-
1
the positive sign fcr a pump, the ne~ativc sign for
a
turbine.
Example: Pump:
a,
sin
p1
r,
b,/(@,,
sin
P,,
rcr
b,,)
=
I,]
;
rrr
=
1
P,
=
PC.,
=
20';
1,;
=
0,l; s,,,,/Ln,
=
0,l;
h,,/N
=
0,Ol;
GI/@,,
-
1.2;
z
=
6;
Qe,
=
0,833;
r,/i-,
=
2;
xlrz
=
1;
p,,
=
20";
D2
-
PI
=
0,087;
Q),
-
dll
=
-
0,3; \v1,,,/\v
,,,,
=
1.1.
This gi1.e~
j.
=
0,429.
Strictly speaking, the critical point makes
i
a
minimum
3s
a
function of
I-,,
and
8.2.3.4.
Axial
n~ccllines
I.
Critical point on thc suction face. Iil gcncral
r-,,
=
r,.
I-Ience
(8.2.3-3)
(PI
-
~.,,)/e
=
OV;,
-
\v:)/2
+
g
(her
--
A,)
k
11;
g
H
s,/L,,
.
(S.2.3
-
I
1
j
With
b,
=
b,,, rcr
=
r,
Eq.
(8.2.3
-
5)
is sintplificd to
wA,
=
\v1
(@,
(sin
fl
,/sin
per)
.
(8.2.3
-
123
An
application of
Stokes'
theorem to obtain
p,
-
pcr
in
(8.2.3-4)
according to
(8.2.3-6)
does not work since
/I
=
90:'.
Assuming
a
linear \.ariation of pressure along the cil-cum-
fcrence according to assumption i), the differential pressure
Ap
bctlveen pressurc and
suction face at the critical point depends as follows on
p,
-
]I,,
'To
simplify the task, the following two cases arc distinguished:
Case a): Triangular distriburion of the
dinerential pressure along the blade
due
lo
an
angle of attack (see Fig.
8.2.15
c). Hence
where
CAG
is tlle lift coefficient of the blade in cascade,
tiv,
the undisturbed trelocity
(obtained from the \relocity triangles
as
nl,
=
(w,
+
,v2)/2).
Wit11 the relatiorls of
U[iucrs-
fdd
C,,
=
(2
t/L)
Ac,/\o,,
of
Elrler
Ac,,
=
g
H
1,;
'/I(,
the blade tip velocity
11
2
lv,
,
h,
=
0,
the
blade tip velocity coefficient
Ktc
=
u/J=
and
(8.2.3-2),
the relations
(8.2.3-
11)
(8.2.3-
14)
yield

Case b): Elliptic distril)utic)n of the diffcscntinl prcssure ;11011g
tllc
bl:~dc due to
a
vanishi
angle of incidence on
;I
blade section with circular skcleton. klencc (Fig. N.2.1Sc)
2
AP
=
(21x1
,o
[A,
,v,.
In this case
h,,
-
It;
s,
2
t
rlT
'
2
.
=
(1
sin
1
y
-
1
+
(N
+
-
+
--)($)
-
@cr
sin
Bcr
Lm
nL
The --sign before
12;
and the exponent of
rl,
holds true for a pump, and the
a turbine.
Example:
Kaplan turbine, case
a:
Ku
=
1,53;
P1
=
20,5"; hit
=
0,03; sm/L
=
0,2;
/1,
=
22
Q,,
=
0,85;
@,
=
0,9; t/L= 1;
h,,
=
1,5
m;
Kc,
=
0,572; q,
=
0,95. This results
In
I.,
=
0,156.
In an
examplc for case b): h,,
=
0,SS; s,/L,,
=
0,5. This lesscns the term (kc
L,)
(cos
PI
i~tr),
from 0,023 to 0,0174. Also the last term
(2
t/n L) (cos
reduced
iroln
0,354 to 0,226. Thus
Rb
=
0,023.
At a value
I.,
=
0,156, a draft tube efficiency of q,
=
1
-
[,
=
0,85 gives a cavitati
index
a
a
=
~,Ku~
+
(A
+
tl,)Kc;
=
0,7.
The plant, having barometric pressure head of
B'
=
9,5 m, a critical pressure
hea
It,,
=
0,25 m and a head of
H
=
27
m,
requires a suction head
hS=B1-h,,-OH=- 10,52m.
Usually the essential pitting
by
cavitation in the outermost part of a runner
from the
ttvo modes of operation
a
and
b,
described above. Since the outer1
tar? turbine of a high specific speed Francis turbine runner
(n,
>
200) is nearly o
caaxial cylinder, the
preceding considerations and hence the validity of equat
(5.2.3-
17)
can also
bc
extended into this type.
11.
Critical point at the inlet edge of rotor: The solution of this case can
approximately for semiaxial machines, when operating with a critical point on
t
inlet edge. In this case the distribution of the differential pressure alon
triangular
like. Hence the solution for
R,
(8.2.3-
15) can be applied. Since t
bzsed more on an estimate: a more exact approach is presented, which contains also
cascade factor and the curvature of the inlet edge.
Denoting the velocity peak at the critical point by
rv,,,,
1,
follows from the ene
theorem between the points 1 and
cr
lying now on a streamline along the contour
of
blade by
1.
=
(w,,/w,)~
-
1
=
k2
(KUJK~V~)~
-
1,
where
Kw,
=
IV,/(~~H)'~~,
Ku
=
u/(~~H)"~ follow from the velocity triangles and
k
=
w,",,/u,
may
be
approximated by the following simple hydrodynamic model for the blade
straight cascade.
300

bs is wcll-known,
the
critic:{! point ivith its velocity pc;lk at the inlet cdgc of
n
hl;\dc
reslllt~ froril tl~c ;~nglc of attack
6,.
the zcro
lift
directio~l of the b1:lcie ni;tkes
\\,irli
tile
,,,,,iist~rrbed velocity
IV,
due to thc vclocity triangles. Jlcllce the pl;~nc potcntinl
flon.
,rou~~d the vane hi~s
a
circulation, sce
(5.2-38)
,v~lere
Ac,,
is the difference of the whirl
components
of thc absolute velocity at
the
stiltions
1
and
2
due to the velocity triangles,
r
thc pitch of the straight c;~scadc formed
by
thc rotor
\rallcs by unrolling its cylindrical scction into a plane.
consider
a
model of a single plate, chord length
L,
for the vane.
As
is rell-known. its
prcssLrre centre is
a
distance
1.14
from the leading edpe. Moreover. a str;\ipht vortex
filament with the circulation
I'
at this point of
lift
aitack is
21
hydrod!.narnic cqiiivalen~
,f
the plate
[5.14].
r
induccs at the inlet edge the velocity
TO
this must be added the velocity originating from the shnrp cur1:ature
l;R
at the
head.
For this purpose, an ellipse of chord
L
as its major axis, a~?d the rnaxilnum profile
thickness
11
as the niinor axis, in
a
flo~v with undisturbed velocity
11..
sin
(j,.
normal to
the chord, is chosen as a model. Accordingly the velocity at the vertex
or
the rnajcr axis
15.31
(Fig.
8.2.1
5
d)
w,
=
w,
sin
8,
(1
+
L/h),
(8.2.3
-
22)
where
6,
is the angleof attack,
w,
the undisturbed vclocity.
Since the velocity peak
\r,
is niore induced by the curv;iturc
1,'R
of the inlet cdge at
the
vertex
of
the ellipse than by thc tl~ickncss ratio hi:,, thc know11 curvature
I
R
at tl:c vertex
of
an ellipse is remenibered as
1/R
=
2
12/h2.
(See Hiittc
I.
des Ingcnieurs Taschenbucl?.
M;ithematik p.
139.
Berlin: Ernst
1955).
Hcnce
11
=
(2
RL)'
'.
Thus
I\.,,
reads In term\ of
the v;!ne's inlet ct1rvatur.e
As
is well-known
[6.3],
the physical angle of attack
5,
follows from the
lift
coefficient in
the cascade
c,,
and the cascade lactor
x
(sec
6.2
-
50)
by
sin
6,
=
[,,/(2
n
x).
'
1
Introducing the relation of Rr1uer..?feltl(6.3-
4)
fsr
c,,,
Etrler's equation
,I(.,
=
<IF!
11,
and
the cocfficient of the bl:lde speed
Ku
=
uj(2
Ii)'12
yield
where
II
is the periplieral blade tip velocity,
t/L
the pitch to chord ratio,
rl,,
the peripheral
cfliciency of the miicl~ine, with the negative exponent for a pump and
t
IIC
positive for a
lurbinc.
Sllb~titutin~ also for
in
(8.2.3-21).
Esler.'s equation and employing the blade tip speed
cmfficient
KII
result
in
Sun1lniag itp
,v,-
alld
ir,
gives the desired rrlaximum velocity

\\',rill,
=
)?II
t
\VR
.
I4cltcc
thc dc\ircd cocfficiclit
1,
(8.2.3
I9),
also
ticctlc~f for
;i
k
=
(1,'n)(r/l,)(tl,?
','h'[r2)
(
1
+
(1/2x)[I
+
(1.12
R)'/*]).
Examl~lc:
Knplon
turbine:
t/L
=
1.2:
KII
=
1.4;
L/11
-.
200;
x
=
1;
=
?On;
11.
=
0,
Kc,
-=
0.5;
K\r.,
=
1,15
yield;
k
=
1,2;
1.
=
0,24.
Plc~~cc
a
machine i~ith thc draft
tu
efficiency
tl,
=
0.88
has
a
=
0,75.
8.2.4.
Fundarllentals
of
pitting
rate
as
function
of
velocity
8.2.4.1.
'Introduction
Ercsion (pitting)
by
cavitation occurs usually downstream of the rear of
a
s
attachcd sheet-like cavity (Fig.
8.2.16).
According to tests of
KIIII~~
[8.6],
the pitting
for soft
aiurnin~~m
may vary,
(8.2-22),
undcr a definite modest cavilation degree
(in
neighbourhood of the critical cavitation index
a)
with up to the sixth power
of
velocity, hence
n
>
6
in
(8.2-22).
With a rising degree of cavitation (falling
a)
this power rnay drop to zero. The
same
occurs when
a
increases abovc its critical value.
Allowing cavitation erosion and its regular repair is common practice to savc excavati
to excessive subrncrge~cc. hlodcrn sets
especially
in developing countries are often planned
larger
output 1h:l.n
necessary
in thc first pcriod of the plant's
operation.
Usua!ly under this
needed
rer\
ice anaj from thc bep, the ~nachillc cnvitates.
Ir.
1
5ccu11d
stas:: sonletimcs ;he unit power is enlarged
by
lifting the head of the plant
by
means
lifting
the
crebt height of its dani
12.341.
At the same spccd, this increases as well the rclative vel
ant1
;~lso the ansle of
incidence
and hcncc the susccptibllity to pitting. Here again the proble
zc..lu=nce of repairs ariscs.
0-
----
cl
P
.
.-I;
b
wd
!
//I//./
I
fd
-.-.
.-
2
Fig.
S.2.1b.
Erosion due to a bubble moving around a quasi resting wall-attached cavity
a)
matic view with re-entrant jet and important stations
the bubble
passes.
b)
Strearn tube
elem
the screenirig section ahead of the profile. c) Detail of re-entrant jet
of
local depth
b.
302
1'
\
.I-
///I
/////
'r
'
Ll
Li

~llercfore in the lollowing
8
theoretical approach
is
made
to help understi~nd the linkage
bclwccn pitting ratc and relative velocity.
8.2.4.2.
Asslrnlptions
aho~~t
wall-attached cavity and
its
erosion
consider a wall-attached static cavity with a re-entrant jet (Fig. 8.2.16a).
A
stream tube
of
cross sectional area
A,
before the body at station
1
in part encloses the cavity along
the path marked by the stations 1,
3,
5,
7.
This stream tube is ~trranged around and 2long
a
streamline tliat inlersects the stagnation point
7
downstream of the rear of the cclvit~..
This stagnation point results from
a
splitting of the flow in this stream tube at the point
7
inlo the re-entrant jet and
a
branch oriented downstream lollowing its original direc-
tion.
A
vapour bubble moves along this stream-tube slipping against the liquid and hence
with an added Inass especially near the stagnation point with its stream\vise pressure
gadient. One consequericc of this pressure gradient is the propulsion of the re-entrant jet
the wall shear force acting on it.
Thus the sudden deceleration of this bubble together \\.it11 its added mzss before the
point
7
results in a strong pressure rise along the streamline towards this
point.
In consequence of the momcntum theorem (here the so-called "Rocket effect" after
Chir~cholle
[S.113]),
the pressure increase is amplified by tlie sudden shrinkage of the
bubble
~lolume, when approximating to the stagnation point
7.
This shrinkage results from the compression of the bubble by the rising pressure around
it
but mainly by the sudden condensation of its dominating vapour content. when the
prcssure rises above the steam pressurc of the liqt!idI Thispulsating pressure
due
to the
implosior? of tlie bubble in
7,
causes pitting. According to experience pitting rate is
greates: around the stagnation point
7,
past the rear of the static cavitj.
The pitting might occur esclusivcly in the above cited stream tube that crosses the
stagnation point
7.
8.2.4.3.
licalization
of
the approach
The
unit volume entcrinz the above stream tube of cross section
A,
at station
0
before
the body (Fig.
8.2.16a), velocity
w,,
may have
z,
spherical nuclei, radius
R,.
Ncnce
tht:
time, the unit volume needs, to pass the section
t
=
l/(\v,
A,).
Assume that all the nuclei passing
A,
also collapse at station
7.
Thus the collapse rate
of
bubbles there
i
=
z0/t
=
zO
A,
\ti,.
(8.2.4
-
2)
The
crosion rate (pitting rate) is assumed proportional to
i
and the pressure
pi,
irlduccd
by
tlie bubble collapse. Hence
where
C,
is
n
parameter due to the wall material and cavitaiion degree, e.g. expressed in
terms oflo
-
a,,(.
Knowing how
pi
depends on
\v,
will answer the problem of erosion rate
n't,.,
as a function of the flow
w,.
For this purpose the following considerations are made.

Tlic b~15blc iliiploding
::t
7,
undcr khc extcrnal pi-cssu~.~ p7 froni its initial radius
d,
-
0.
to
its
final
rildi~~s 11::s ttlc irnplo\ioo ra:c
R,.
Siiicz tlic volumc r.ltio dtle to bu
shrink;~gc
by
condcns;ltio~l, is proport~on:il to
(R,/R,)'
aiid
131
tl~
ardcr
01
lo5, unity
be ~leglcctcd in proportion to it.
I
lcncs
Ruylci,qlt's
fornii~la (8.2-20) brillgs
~i
=
[(2/3)
(p71eL) (R,lRi)31
'I2
Imagine that
Ri
ib siiddenly stopped, then the water hammer-induced pre~surep~(g.2-~
becomes
Pi
=
QL
0,
Ki
where a,
=
(QJE~)"~, EL the bulk modulus of liquid, a, the speed of sound of the
pu
liquid, surrounding the bubble.
Assume that the gas remaining within the bubble of radius
R, behaves isentropicall
between
7
and station
3
at the entrance of the critical zone (Fig. 8.2.16 a), radius
vapour pressure
p,, and expressing an eventual gas diffusion into
the
bubble betwee
arid
3
by a factor
%(>
I),
R,
reads
Ri
=
R
,
whert:
x
is the adiabatic exponent.
The
pressurep, at
7
under which the bubble, radius
R,,
implodes is assumed to origin
from the sudden cessation of the velocity \v7, due to the bubble's added liclui
proportional to
R:.
Hence
JOLI~OY.V~Y'S
water hamlncr shock (8.3- 54), now
mass large compared
with that of the gas remaining (being proportional t
coilsequently in
a
two phase mixture environment, having the velocity of sound,
differing from that of the liquid,
a,, results in
p7
=
gaw,,
where
Q
is the density of the two phase mixture.
Kow
the momentum theorem is applied to the bubble between tile st:~tions
~vhirh
the bubbIe has the velocities
\v6
and
\v7
(Fig. 8.2.16a). Its added liquid
m
being proportional to
R:
and
R;,
now only relevant (as the mass of the bubble
co
is ncg!igible compared with them). Hencc with
tv,
=
k,
IV,
W7
=
k6
\\lo
(R~/R?)~.
Assumi~ig the bubble to cover the cavity section from
5
to
6
(Fig. 8.2.16
a),
len
the mean velocity
kc
tr*,, its travellirlg time interval needed is t,
=
L,/(k,
\v
fi:rther the bubble to have ther: the maximum growth rate from
(8.2-
13) tin
pressure, which depends on
boo
after Parkill
[S.112]
yielding the bubble growth rate
(8.2-14) and neglecting the initial bubble radius
R,
at
5
against
R,
t,
=
L,l(k, 1~0)
R
=
R,,,
tc
=
[(2/3)
C2
w$/@]
'I2
[L,/(k,
wo)].
Imazine that In the so-called screening section (Fig.
8.2.16
b)
from station 1 to
3,
len
La.
tke radius of the nucleus considered decreases in consequence of screening fr
R,
=
R,
at the inlet
1
to
R,
at the exit
3.
By
a
simple consideration after Raabe
[8.
R3
=
C3/\~0,
where
C,
=
(3/2)'12
n
to
R:
v
ra/(k,
rp
La dRlan),
304

,"hzrc
zo
is the nu!nber of nuclci pcr
111tit
VO~~II~IC
;110ng
L,,,
KI
the r:ldius
of
~~uclclls
entzring
the
~ection
I-.,,,
\*
IIIC
kincnlaric viscosity of thc liqtli(t.
i-,
the mean sadius of
slrcnrnli~~c curvnturc in
I.,,,
(].'is.
8.2.16
a).
k,
(
<
I)
tt~c factor. that relatc~ thc bubblc
velocity
in
the
screcrlitt:: scction to
w,
by
I\),,
=
kt,
H.,,
cp
thc portion of silrfacz
/J
in tile
]iCI~lid plla~i illong a main stream line
in
the screening scction and pcrpcnclicuiar to the
elclllc~it
(711
(Fig. 8.2.
I6
b).
~hrough the litter surface passes the cross
flow
of nuclci, which are screcncd tonlards the
cclltre
of
curvati~re
P
in the screening section (Fig. 8.2.16 b).
~:'H/?II
is the gradie~~t
of
the
bubble rndius,
tilt
nuclei have towards the point
P.
Inserting
R6
fl-orn (8.2.4-9) into (Y.2.4--S), thcn
\I?,
forp, into (X.2.4-7), then
p7
for
R~
into
(82.4-4), the11
R3
from (8.2.4-
10)
into
(8.2.4-6), then
Ri
into (8.2.4-4) and finally
di
fl.0111
(8.2.4-4) i:tto (8.2.4-
5)
gives
an implicit rc1;ition for the prcssure
11,
due to bubble
implosion in
7.
Explicitly written down, tlie lattei gives
8.2.4.4.
El-osion
rate as
a
fi~nction
of
thc vclocity
lo,
Inserting (8.2.4.- 11) into
(8.2.4
-
3)
gives the erosion
rate
as a function of the \,elocity
\\,,
For
an
interpretation of the last relation the celerity
(=
vclocity of sound) of tlic t\vo
phase misti~rt.
'a'
in the =&ding section
Id,,
(Fig.
5.2.1Gi~)
hiis to be
presented
in tcr-ms
of the velocity
\\lo.
For
this purpose the follo~tting approximate sclation
was
clerived
by
Rcrnl~c
[8.75]
where (Fig. 8.2.16 b)
k,
clctermines the nican velocity of the re-entrant
jet
by
r~,
=
k,\v,,
r'.,
is the mcan dcptll of this flow branch,
I.,,
tlie mean radius of curiarure
this
flow branch has,
r.
the void f'raction of the mixture there.
11
the polytropic cxponcnt the
g:iscous phase has acc~rtling to its equatio:t
of
'itatc
pr:"
=
conht.
Assu~ning
1.1
==
3,3
after the test of
Plrrkii~
[S.
1
123,
x
=
1,4 for air, thc exponent
oT
the
\..t.locity
\\I,
in (8.2.4-
13)
becomes
11
=
5,63. This corresponds nearly to the lal.~est value
of
this exponent according to the tests
of
Knul~l)
[5.6].
For
a
growing degree of cnvitiition (i.e.
with
decreasing
a)
in
coilscqilcnCc of
rhe
thcn
rising
tu:.bidity
of
Ihc
mixture, having
a
void fractioii rising propnrtiorlal to
\i3,
\vitllin
thc
zonr
of pitting. many of
Ihc
bubbles cntraiiicd
may
bc rcpclled from tlic \+,all.
.TIlus
concrury
to
thc u,sulnplio~l
above
the
nunibcr of collapsing bubble
ITI;~~
be constant. Thcrcby ihc cxponcnl drops
by
1
to
4.03.
11
may
be st~pposcd also
that
the tirrbidity around tl~e cavit) incrc;lscs
with
thc \fclocity.
and
hcncc
btinlulates gas diffusion illto
the
bubblc, for which
;!
is
proportional to This drops
thc
cxponcnt
by
thc
1~~111
(3/?)[2%,'(2
x
-
I)]
=
33,
so
that
tlicn
rl
bccomcs
2,l.
Assuming tl;c celcrity
'tr'
of
thc rnixture to
be
invcrsciy proportion;~l to the void fraction
3
and
this
10
be
prol~ortion;:I to the
velocity
rv,,
(by
stiniul;~ting thc con\fuctivc tiiffusion). the exl)oncnt
11
nlity
drop
again
by
thc tcrln
(li2)j.?;cl12
x
-
I)]
=
0,7S
resulting
in
11
=
1.31.
For
n
very largc Jcprcc of

ciivititticn (d~tc
to
it
cnvit:ttion iridex
far
below tlic critie~l), the dist;!ncc.bztwcc~i n~lj;~cellt implo
htthblcs bccomcs
$0
sni;lll, (hilt t!ic cclcrity of thc liqrlid
tr,.
=
,/p,.lll,.
rcs;>or\siblc for
tllc
iln
prcssurc of tllc ir~iplo~lirig birl~l~lc l1;1s to
be
suhstit\~t!:d
by
that of
111~
t~iisturc
'11'
(8.2.4-
14)
Assuming then
'ti',
;IS
previc~usly, to bc irlvcrscly prol)ortionnl to
\yo,
the zsponcnl
tt
dro
the term
2
z/(Z
z
-
I)
=
1,5, which Ic;tcls finally to
rr
abc)ut xro. 'Therchy the decrcasc oft
w,
according to the tcsts of
Ktrcrpp
[8.(1]
can bc rcalizcd on tllc basis of
IC~ISO~~~~C
physical
stio\\~n abovc. Usu;~lly
a
wall-attacliccl cavity with
rc-entrant
jet consists of a scqucucc of alter
cavitics originating from the wall
and
then tlctaching tlicnisclvcs ant1 then ccdlapsing. Herc the
cyc niny only observe thc maximum
-
cavity Icngtli. The cavity starts from its fixed hc:ld and its
0-ows with time rlnpsctl
I
by
Jar
(rr
=
thermal diTl'itsivity). Its growt!~ ends when thc jct cuts
c'.
cavity hcad frorn thc wall. As the vclocity of the rc-cntrant jct incrcascs with
NPSH,
the
cavity Icngth
L
observable is dccrcosi!ig with
hrPSII
increasing.
The frcqucncy of this
alternation is
controlled
by a ccrtain
Strolrllal
nurnbcr formcd by
L
and thc undisturbc
8.3.
Water
hammer
8.3.1.
Celerity,
fundamentals
of
method
of
characteristics
in
c,
p-plane
Consider
a
real compressible iiquid, density
Q,
bulk modulus
E,.,
within
a
straight
pi
having a constant cross sectional area
A,
diameter
D,
with a thin wall, thickness
s
compared with
D,
of elastic material, modulus of elasticity
E
(Fig.
8.3.1
a).
A
press
p~ilse
with
cross sectional-averaged value
tlp
propagates along the pipe axis
s-direction rzlative to the liquid with celerity
n.
-
dD/2
a)
b)
p-
Fig.
8.3.1.
Plicnomena in
32
I.
6fJjf
front, along
of
sound) rnovirlg the
tr:
pipc
:I)
with lncrernen axis celerity seen (vel
A+dA
x
obscl-vcr in the wavc front.
b)
ocdc
r---
dilatation due to pressure in
w
rnent.
Sirnr~itaneously disturbances of fluid density and velocity with
thc
cross section
averaged
values
cl,o
and
dc
also propagate themselves in the x-direction with cel
Ail
disturbances are assumed as time-independent.
Moreover an increment of the pipe's cross section
dA
propagates together
with
pressure pulse
dp
with celerity
n
in the x-direction. First the problem rises to obtain
celzrity as
a
function of the known properties of the liquid and pipe.
Obviously an observer moving relative to the fluid with cclcrity sees
a
stcady motion. Accordin
GLlli/ei's
principle
of
relativity such
a
coordinate system is equivalent to
a
stationary on
latter is
an
incrtial frame of reference uniformly and rcctilinearily moved. Hence assuming
the theorems of rncclianics (mass conservation, momentum thcorem) can bc applied to the fram
reference, that moves with celerity
a.
Obviously the above consideration about the equivalence of both the systcn~s of
reference
sc;od, if the fluid nioves with constant velocity or is
at
rest.
The
latter is assumed since a co
rnotion of the fluid, according to
Girlii'ei's
principle, cannot contribute anything to a phen
of ~liechanics like celerity.
Locating now the observer in the wave frmt of the pressure pulse, in which all the
val
p.
Q,
c,
A
experience
a
steplike increment
by
dp,
d~,
dc,
dA
(Fig.
8.3.1
a)
that
lasts
attcnuatedly, the followil~g is observed.
306
