Пьянков В.П. Тексты лекций по элементарной математике
Подождите немного. Документ загружается.

В.П.Пьянков Избранные разделы элементарной математики
4.1. При каких значениях р уравнение
0),( pxf
имеет оба корня на промежутке
);(
];(),;(),;[
?
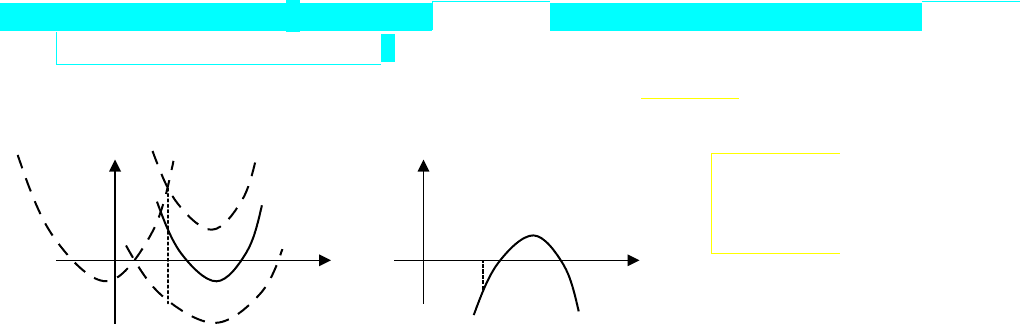
Сделаем рисунок, соответствующий условию с промежутком
);(
.
Этому условию равносильна система
B
x
D
fA
0
0)(
)3(
)2(
)1(
,,
,,
(Знаки неравенств справа в скобках
соответствуют другим видам
промежутков.)
Неравенство (1) необходимо для того, чтобы отмести трехчлены, у которых корни располагаются по разные
стороны от точки α (на рис. параболы вида 1). Неравенство (2) – для того, чтобы отбросить трехчлены, у
которых нет корней (параболы вида 2). Неравенство (3) – для того, чтобы отмести трехчлены, у которых
61
A>0
α
3
х
у
2
1
A<0
α
х
у

В.П.Пьянков Избранные разделы элементарной математики
корни находятся левее точки α (параболы вида 3). Неравенство (2) учитывает случай, когда корни
одинаковые. Если из текста задачи ясно, что корни разные, то надо писать
0D
.
Пример [4], №6.55. При каких значениях k корни квадратного уравнения
023)2(
2
kkxxk
действительны и оба больше 0,5? Ответ:
)2;17/16[k
.
Пример. При каких значениях параметра k уравнение
023)2(
2
kkxxk
имеет только корни,
большие 0,5? Ответ:
]2;17/16[k
.
При такой формулировке задачи надо рассмотреть еще линейный случай, получающийся при
2k
, в
котором уравнение имеет единственный корень
5,03/2 x
.
Пример. При каких значениях параметра k уравнение
023)2(
2
kkxxk
не имеет корней,
меньших либо равных 0,5? Ответ:
]2;0(k
.
Такое может быть, 1) когда уравнение имеет только корни, большие 0,5, т.е. при
]2;17/16[k
, либо,
2) когда оно вообще не имеет корней, т.е. при
0D
,
0171617 kk
;
)17/16;0(k
.
62
В.П.Пьянков Избранные разделы элементарной математики
4.2. При каких значениях р уравнение
0),( pxf
имеет два положительных
(отрицательных) корня?
Это частный случай предыдущего. Для него требуемую систему можно составить, используя условия
теоремы Виета:
ACxx /
21
,
ABxx /
21
.
Неравенство (1) – условие одинаковости знаков корней. Неравенство (2) – условие
существования корней. Его надо включать в систему, т.к. при выполнении условия
(1) корни могут и не существовать. Условие (3) совместно с другими условиями
гарантирует положительность (отрицательность) корней.
Пример. [8], №9.101. При каких значениях параметра р оба корня квадратного трехчлена
59)1(2
2
pxpx
отрицательны? Ответ:
);6[]1;9/5( k
.
Пример. При каких значениях параметра k уравнение
023)2(
2
kkxxk
имеет только
положительные корни? Ответ:
);2[]16;( k
.
Опять же при такой формулировке надо рассмотреть еще линейный случай, получающийся при
2k
.
63
0)(/
0
0/
AB
D
AC
)3(
)2(
)1(
В.П.Пьянков Избранные разделы элементарной математики
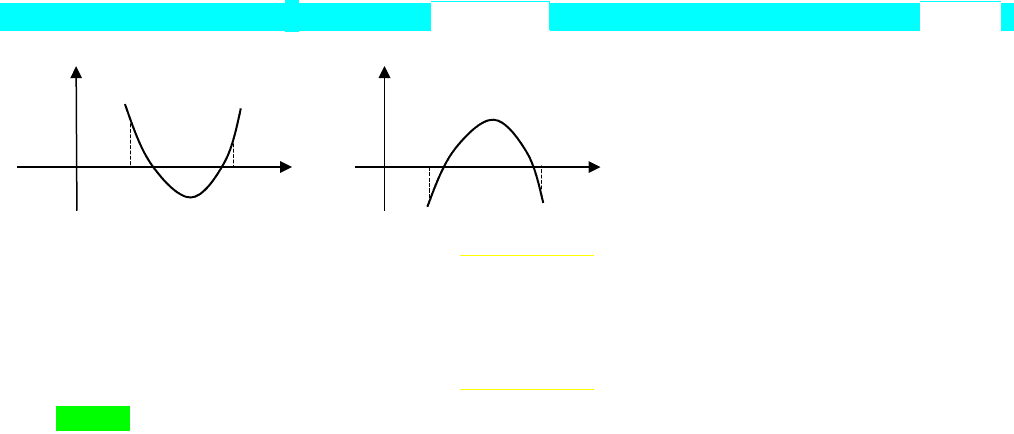
4.3. При каких значениях р уравнение
0),( pxf
имеет оба корня на промежутке
);(
?
Условию равносильна система
B
x
D
fA
fA
0
0)(
0)(
Пример [4], №6.58. Найти все значения n, при которых корни уравнения
02)1(
2
xnnx
будут действительны и оба по модулю меньше 1.
64
A>0
β
α
х
у
β
A<0
α
х
у

В.П.Пьянков Избранные разделы элементарной математики
Решение.
1
2,1
x
)1;1(
2,1
x
. Значит, условиям задачи равносильна система
11
0
0)1(
0)1(
B
x
D
fn
fn
, где
2)1()(
2
xnnxxf
.
1
2
1
1
08)1(
0)21(
0)21(
2
n
n
nn
nnn
nnn
2/)1(
2/)1(
016
0
0)32(
2
nn
nn
nn
n
nn
nn
nn
nn
n
21
21
016
0
2
1
3/1
016
0
2
n
n
nn
n
223
223
1
n
n
n
Ответ:
);223[ n
Примечание. Если в условии задачи п. 4.3 записан промежуток другого вида
);[
,
];(
или
];[
, то система претерпевает изменения аналогично тому, как указано в пункте 4.1.
В заключение напомним о «прямом» способе. Не следует забывать о нем. Иногда с его помощью
получаются простые системы.
65

В.П.Пьянков Избранные разделы элементарной математики
Оценки ограниченности функций
Ниже записана сводка оценок, наиболее часто применяемых при доказательстве неравенств и
решении уравнений с ограниченными функциями. Эти оценки являются неравенствами, справедливыми на
некоторых промежутках изменения переменных. Причем в случае нестрогого неравенства на промежутке
обязательно имеется такое значение переменной, при котором выполняется равенство (достигается граница
оценки).
Алгебраические оценки
1) Квадратный трехчлен всегда ограничен сверху или снизу. Он в вершине параболы имеет минимум
(максимум), если 1-й коэффициент положителен (отрицателен).
2)
0
2
cba
0a
и b,с
R.
Конечно, в сумме может быть иное число неотрицательных слагаемых (например, несколько
квадратов), степень с другим четным показателем или корень иной четной степени.
Равенство нулю суммы неотрицательных слагаемых может быть только тогда, когда все
слагаемые обращаются в ноль:
66
0
0
0
c
b
a
В.П.Пьянков Избранные разделы элементарной математики
3)
ABBA 2
22
А,В
R. Причем равенство выполняется только при
BA
.
ABBA 2
22
А,В
R. Причем равенство выполняется только при
BA
.
Это следствия из очевидного неравенства
0)(
2
BA
.
4) Неравенство Коши между средним арифметическим и средним геометрическим двух чисел:
ab
ba
2
а0, b0. Причем равенство выполняется только при
ba
.
Это неравенство получается из предыдущего, если сделать замену
22
; BbAa
.
5) Неравенство для суммы обратных положительных чисел:
2
1
1
a
aaa
0a
. Равенство выполняется только тогда, когда
1a
.
Это неравенство получается из предыдущего, если сделать замену
ab 1
.
67

В.П.Пьянков Избранные разделы элементарной математики
Для отрицательных чисел:
2
1
a
a
0a
. Равенство выполняется, когда
1a
.
Обобщение:
02
1
a
a
a
. Равенство выполняется, когда
1a
.
6) Неравенство Коши для n чисел
n
n
n
aaa
n
aaa
...
...
21
21
0,...,0 ,0
21
n
aaa
.
Равенство выполняется только тогда, когда
n
aaa ...
21
.
7) Неравенство Коши-Буняковского в векторном виде:
bababa
;
в обобщенном развернутом виде:
22
2
2
1
22
2
2
1
......
nn
bbbaaa
nn
bababa ...
2211
22
2
2
1
22
2
2
1
......
nn
bbbaaa
Rbbbaaa
nn
,...,,,,...,,
2121
68
В.П.Пьянков Избранные разделы элементарной математики
В векторном виде неравенство легко доказывается, т.к.
cos baba
,
1cos1
.
Равенство справа или слева выполняется только тогда, когда
ba
||
, т.е. когда координаты
вектора
a
(числа
n
aaa ,...,,
21
) пропорциональны координатам вектора
b
(числам
n
bbb ,...,,
21
). Равенство слева (справа) выполняется в случае, когда
ba
– векторы
направлены в разные стороны (
ba
– в одну сторону), т.е. когда коэффициент
пропорциональности координат не положителен (не отрицателен).
Еще справедливо более сильное неравенство:
nn
bababa ...
2211
22
2
2
1
22
2
2
1
......
nn
bbbaaa
Rbbbaaa
nn
,...,,,,...,,
2121
.
69

В.П.Пьянков Избранные разделы элементарной математики
Сравнение функций с аргументом и между собой
Напомним, что графики взаимно обратных функций симметричны относительно прямой
xy
. Если
они пересекаются или соприкасаются, то только на ней.
1) При
1p
xx
p
1 0;x
,
xx
p
) ;1[ x
.
При
10 p
наоборот:
xx
p
1 0;x
,
xx
p
) ;1[ x
.
Равенства только в точках
0x
,
1x
(см. рис.)
2) Если
445,1
1
e
ea
, то
) ;0( log xxx
a
,
xa
x
Rx
.
При этих значениях а графики
xy
a
log
,
xy
и
x
ay
не
имеют общих точек.
При
e
ea
1
графики касаются в точке
718,2ex
.
70
x
1
1
y
y=x
p
при 0<p<1
0
y=x
p
при p>1
y=x
