Пташкина-Гирина О.С.; Щирый В.Д. Гидравлика. Учебное пособие

Подождите немного. Документ загружается.

силы, имеющие потенциал. Наибольшее значение из них имеют

силы тяжести и силы инерции.

3.3. Основное уравнение гидростатики.

Эпюры гидростатического давления

Это уравнение есть уравнение равновесия жидкости, нахо-

дящейся под действием только сил тяжести.

В уравнении Эйлера (3.11) проекции ускорений для земных

условий равны:

Х, У = 0; Z = -g.

Тогда уравнение (3.11) можно представить в виде

сgdz

−

(3.12)

Уравнение (3.12) является дифференциальным уравнением

равновесия жидкости, находящейся под действием сил тяжести.

Преобразуем его. Поскольку

, то

Zd =













, т.е. в любом

случае













всегда остается величиной постоянной, но запишем

ее по-иному:













= idem; (3.13)

idem – здесь и в дальнейшем употребляется только в смысле «од-

но и то же», т.е. имеющее одно и то же значение в рассматривае-

мой области (в объеме или на линии) лишь в данный момент

времени, в отличие от const, означающей постоянство величины

во времени. В выражении (3.13) Z – геометрический напор;

пьезометрический напор;













- гидростатический напор.

Проиллюстрируем величину













рисунком 3.10.

Рис.3.10

Для точек 1 и 2 в сосуде

; (3.14)

так как Z

– Z

=h, то







γ+=

−

hpp

(3.15)

Уравнения (3.13), (3.14) или (3.15) называются основным

уравнением гидростатики.

Вывод: потенциальная энергия в любой точке покоящейся

жидкости является величиной постоянной.

Эпюры гидростатического давления есть графическое выра-

жение закона изменения давления по глубине жидкости.

Рассмотрим несколько типовых случаев.

1. Сосуд с вертикальными плоскими стенками заполнен

жидкостью на глубину h и открыт сверху, т.е. на поверхности

действует атмосферное давление р

ат

(рис.3.11).

Рис.3.11 Рис.3.12

Согласно уравнению гидростатики атмосферное давление

передается равномерно по всей глубине h, а давление от столба

жидкости - по линейному закону: p = γh. Так как сосуд окружает

среда с атмосферным давлением, то действие атмосферного дав-

ления через жидкость на стенки компенсируется давлением из-

вне, т.е. силовое воздействие на стенки сосуда окажет только

давление столба жидкости.

Гидростатическое давление направлено по нормали к стен-

кам сосуда согласно его свойству.

2. Сосуд с вертикальными плоскими стенками заполнен

жидкостью, на поверхности которой создано избыточное давле-

ние р

(рис.3.12). В этом случае силовое воздействие на стенки

оказывает как избыточное давление на поверхности, так и давле-

ние от столба жидкости.

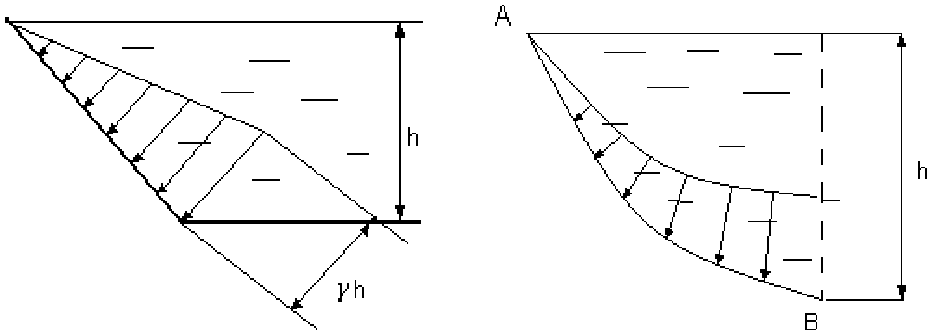
3. Сосуд с наклонной плоской поверхностью, открытый

сверху (рис.3.13).

Рис.3.13 Рис.3.14

Построение эпюры аналогично предыдущим случаям.

4. Сосуд, стенка (стенки) которого имеет криволинейную

поверхность, например АВ (рис.3.14).

Для построения эпюры гидростатического давления, дейст-

вующего на поверхность АВ, необходимо через определенный

интервал по глубине h провести касательные плоскости к кривиз-

не поверхности и к ним по нормали линии действия давления. За-

кон изменения давления в этом случае повторит форму криволи-

нейной поверхности.

3.4. Сила гидростатического давления

на плоские поверхности

Давление, созданное в жидкости, действуя на поверхности

различных устройств и их элементов, создает силу. Плоскими по-

верхностями могут быть стенки различных резервуаров, тела

плотин, клапаны, щиты и затворы.

Определим величину силы, действующей на плоскую по-

верхность, и точку ее приложения.

Рис.3.15

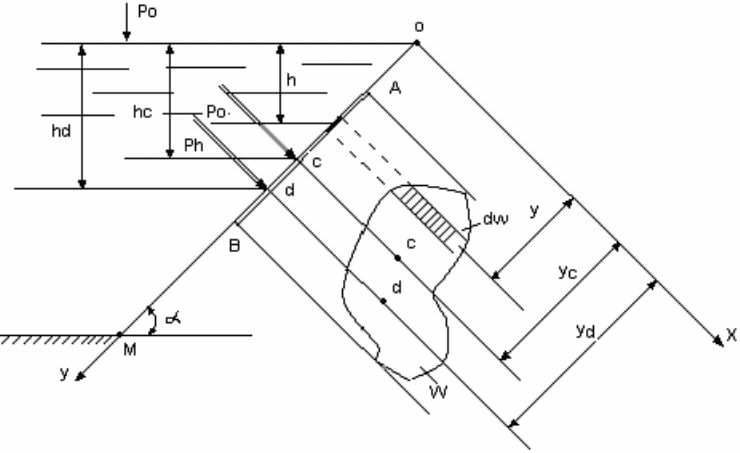
Представим (рис.3.15) сосуд, наполненный жидкостью и

имеющий плоскую стенку ОМ под углом α к горизонту. В плос-

кости этой стенки наметим оси координат ОУ и ОХ. Ось ОХ на-

правим перпендикулярно к плоскости чертежа.

На стенке сосуда наметим некоторую плоскую фигуру АВ

любого очертания, имеющую площадь ω. Из точки О проведем

ось ОХ, нормальную к направлению АВ, т.е. ось ОХ совместим с

плоскостью чертежа. Будем мысленно вращать фигуру АВ во-

круг оси ОУ так, чтобы эта фигура совместилась с плоскостью

чертежа.

Выделим на площади фигуры бесконечно малую поверх-

ность в виде полоски dω, погруженную на глубину h. При этом

расстояние полоски от оси ОХ равно y. Гидростатическое давле-

ние в области бесконечно малой плоскости согласно основному

уравнению гидростатики будет

hpp

Тогда сила давления на элементарную площадку

(

)

dhpdP

. (3.16)

Интегрируя выражение (3.16) в пределах площади ω и заме-

нив h = у·sinα, получим

∫∫∫

ωωω

ydsinpdsinydpP

. (3.17)

Интеграл

∫

представляет собой статический момент

площади фигуры АВ относительно оси ОХ. Из механики извест-

но, что

∫

= y

ω, (3.18)

где у

– расстояние центра тяжести площади фигуры АВ относи-

тельно оси ОХ.

Подставив (3.18) в (3.17) и заменив y

sinα = h

, получим си-

лу, действующую на площадь ω:

(

)

hpP

(3.19)

Это означает, что сила давления P жидкости на плоскую фи-

гуру, погруженную в жидкость, равна произведению этой площа-

ди ω на гидростатическое давление в ее центре тяжести (p

+γh

Из формулы (3.19) следует, что сила Р состоит из двух сил:

силы р

ω и силы γh

ω. Сила p

ω создает равномерную нагрузку и

приложена в центре тяжести фигуры площадью ω. Сила γh

ω соз-

дает неравномерную нагрузку и поэтому точка ее приложения не

совпадает с центром тяжести фигуры. Эта точка называется цен-

тром гидростатического давления; обозначается она буквой d.

Для нахождения точки приложения силы γh

ω применим теорему

механики о моменте равнодействующей силы: момент равнодей-

ствующей силы относительно оси ОХ равен сумме моментов от

элементарных сил:

∫

yydsinysiny

. (3.20)

Интеграл

∫

представляет собой момент инерции I

пло-

щади ω относительно оси ОХ. Из механики известно, что

yII ω+=

, (3.21)

где I

- момент инерции площади относительно оси ОХ, проходя-

щей через центр тяжести.

Подставим выражение (3.21) в (3.20):

. (3.22)

Из выражения (3.22) следует, что центр гидростатического

давления y

находится ниже центра тяжести на величину эксцен-

триситета

3.5. Сила гидростатического давления, действующая

на криволинейные поверхности

В технике, в частности машиностроении, приходится встре-

чаться как с простыми, так и со сложными криволинейными по-

верхностями, подверженными гидростатическому давлению

(сферические крышки резервуаров, стенки круглых трубопрово-

дов, цилиндрических баков, цистерн и т.д.).

Если при определении силы полного гидростатического дав-

ления, действующего на плоские фигуры, по существу произво-

дится простое сложение параллельных сил, то при решении ана-

логичной задачи для криволинейных поверхностей приходится

суммировать силы, имеющие различные направления. Это об-

стоятельство значительно усложняет задачу, требуя применения

специальных расчетных приемов.

Принцип, положенный в основу существующих решений,

заключается в определении составляющих сил полного гидроста-

тического давления по нескольким направлениям, с последую-

щим геометрическим сложением этих частных сил.

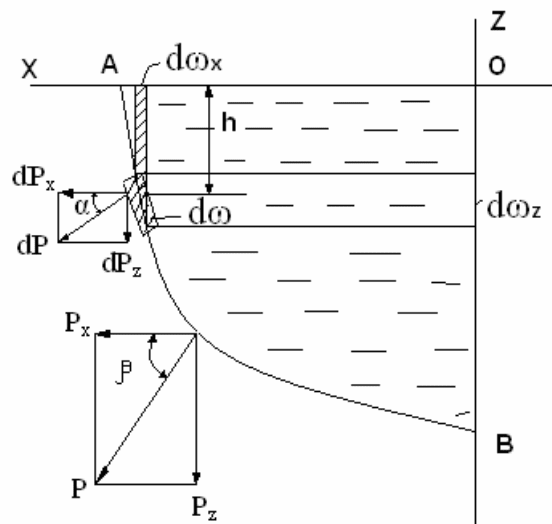
Рассмотрим криволинейную поверхность АВ, подвержен-

ную действию избыточного гидростатического давления только

от столба жидкости (рис.3.16).

Рис.3.16

Выделим на этой поверхности бесконечно малую полоску

площадью dω, центр тяжести которой погружен в жидкости на

глубину h. На эту элементарную полоску нормально к криволи-

нейной поверхности действовует сила dР=γhdω, которую можно

разложить на горизонтальную и вертикальную составляющие:

dР

и dР

. Сила dР наклонена к горизонту под углом α. Тогда

dР

=dР·cosα, dР

=dР·sinα,

или dР

=γhdω·cosα; dР

= γhdω ·sinα.

Из рисунка видно, что dω·cosα является площадью проекции

элементарной полоски dω на вертикальную плоскость, т.е.

dω·cosα = dω

. Следовательно, dР

= γhdω

Тогда горизонтальная составляющая силы избыточного дав-

ления на рассматриваемую криволинейную поверхность

∫

гhdщ

Здесь

∫

является статическим моментом всей площади

вертикальной проекции криволинейной поверхности ω

относи-

тельно свободной поверхности жидкости, совпадающей с осью

ОХ:

∫

Таким образом

= γh

. (3.23)

Другими словами, горизонтальная составляющая Р

выража-

ется произведением площади проекции криволинейной фигуры

на вертикальную плоскость на гидростатическое давление в цен-

тре тяжести этой площади.

Точка ее приложения, т.е. расстояние от свободной поверх-

ности до центра давления определяется аналогично, как и для

плоской поверхности.

Обращаясь теперь к определению вертикальной составляю-

щей элементарной силы избыточного гидростатического давле-

ния, можем написать:

dР

= dР·sinα = γhdω·sinα; dω·sinα = dω

Совершенно очевидно, что hdωх = dW – элементарный объ-

ем, заштрихованный на рисунке, а γdW = dG, т.е. весу жидкости в

этом объеме.

Тогда

.д.

гW

гhdщsinб

∫ ∫

∫

(3.24)

Объем W

т.д.

, являющийся суммой элементарных объемов,

называется объемом «тела давления» - это объем, ограниченный

криволинейной поверхностью, свободной поверхностью и верти-

кальными проектирующими поверхностями.

Суммарная сила Р определяется как

PPP +=

, (3.25)

а ее направление – углом β, величина которого может быть опре-

делена из выражения

tg =β

. (3.26)

3.6. Закон Архимеда. Основы теории плавания

Применим описанный выше прием нахождения вертикаль-

ной составляющей силы давления жидкости на криволинейную

поверхность для доказательства известного закона Архимеда.

Предположим, что в жидкость погружено тело АВСД, огра-

ниченное любой криволинейной поверхностью (рис.3.17). Проек-

тируя тело на вертикальную плоскость и пользуясь формулой

(3.23) нетрудно понять, что горизонтальные силы давления слева

и справа уравновешиваются, поскольку площадь проекции одна и

та же, т.е.

BCD

BAD

ω=ω

, тогда

BCD

BAD

PP =

Рис.3.17

Для определения вертикальной силы давления на погружен-

ное тело рассмотрим отдельно вертикальные составляющие на

нижнюю поверхность АДС и верхнюю АВС.

Вертикальная составляющая силы избыточного давления

жидкости на верхнюю часть поверхности тела

ABC

направлена

вниз и равна весу жидкости в объеме АА

′

СВА.

Вертикальная составляющая силы давления жидкости на

нижнюю часть поверхности тела

ADC

направлена вверх и равна

весу жидкости в объеме АА

′

СДА.

Отсюда следует, что вертикальная равнодействующая силы

давления жидкости на тело будет направлена вверх, она равна ве-

су жидкости в объеме, равном разности указанных двух объемов,

т.е. в объеме тела:

WPPP

ABC

ADC

Арх

γ=−=

. (3.27)

В этом и заключается закон Архимеда, обычно формулируе-

мый так: на тело, погруженное в жидкость, действует выталки-

вающая сила, равная весу вытесненной этим телом жидкости.

На законе Архимеда основана теория плавания тел, в кото-

рой в качестве первых задач определяются плавучесть и остойчи-

вость.

Плавучестью тела называется его способность плавать в по-

лупогруженном состоянии.

В зависимости от соотношения между весом плавающего

тела G и подъемной силой Р

возможны три состояния тела, по-

груженного в жидкость. Подъемная сила при этом приложена в

центре погруженной части тела, называемом центром водоизме-

щения.

1. G>Р

– тело тонет.

2. G<Р

– тело плавает в полупогруженном состоянии.

3. G=Р

– тело в погруженном состоянии.

В первом случае тело тонет, т.к. равнодействующая сила G и

направлена вниз.

Во втором случае равнодействующая сил G и Р

направлена

вверх, поэтому тело всплывает. Однако оно поднимается над по-

верхностью воды лишь до тех пор, пока новая подъемная сила Р

не будет равна весу тела, т.е. G=Р

В третьем случае, когда первоначально G=Р

(довольно ред-

кий случай), тело может находиться в устойчивом, неустойчивом

или безразличном равновесии.

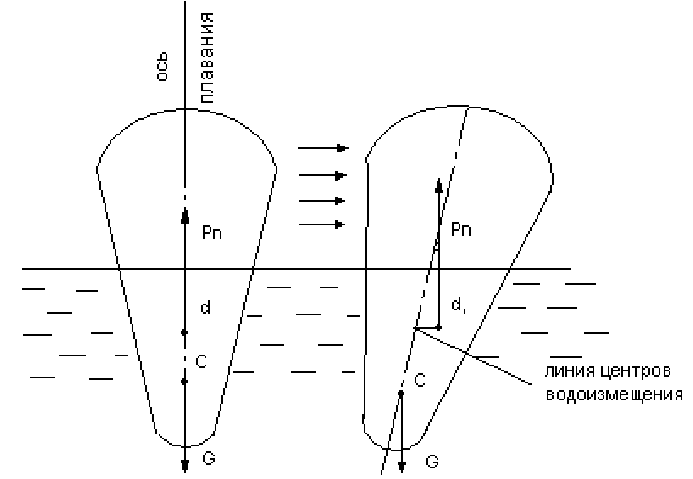
При воздействии на плавающее тело внешних сил, например

ветра, навала судов, оно будет отклоняться от положения равно-

весия (давать крен).

Рис.3.18

Каждое плавающее тело должно обладать остойчивостью.

При этом различают остойчивость статическую и динамическую.

Рассмотрим только статическую остойчивость.