Пташкина-Гирина О.С.; Щирый В.Д. Гидравлика. Учебное пособие

Подождите немного. Документ загружается.

, который равен относительному изменению объема W при из-

менении температуры на один градус:

∆

=β

, 1/град (2.9)

При нагревании жидкости в герметичном объеме в послед-

нем повысится давление на величину ∆р:

Дtв

Дp =

, Н/м

(2.10)

Значение коэффициента температурного расширения β

за-

висит от давления, действующего на рассматриваемый объем

жидкости. В частности, у воды он увеличивается с возрастанием

давления при повышении ее температуры от 0 до 50

С и умень-

шается с возрастанием давления при дальнейшем повышении ее

температуры. У большинства других жидкостей коэффициент β

уменьшается с увеличением давления при любой температуре.

При гидравлических расчетах водопроводных сооружений

температурным расширением воды можно пренебречь из-за не-

значительного изменения температуры и давления воды, а при

расчете тепловых сетей температурное расширение воды учиты-

вают.

Для воды, например, осредненное ориентировочное значе-

ние коэффициента температурного расширения β

равно 14·10

-6

1/град.

2.4. Вязкость жидкостей

При движении жидкости в трубах и открытых руслах каж-

дый слой ее частиц скользит по другому, т.е. внутри жидкости

происходит процесс, аналогичный трению. Силы, возникающие в

результате скольжения слоев жидкости, называют силами внут-

реннего трения, или силами вязкости.

Свойство жидкости оказывать сопротивление касательным

усилиям называют тангенциальной вязкостью.

Рассмотрим движение жидкости, при котором скорости от-

дельных ее частиц параллельны оси трубы. Опыт показывает, что

такое движение жидкости существует в природе (оно называется

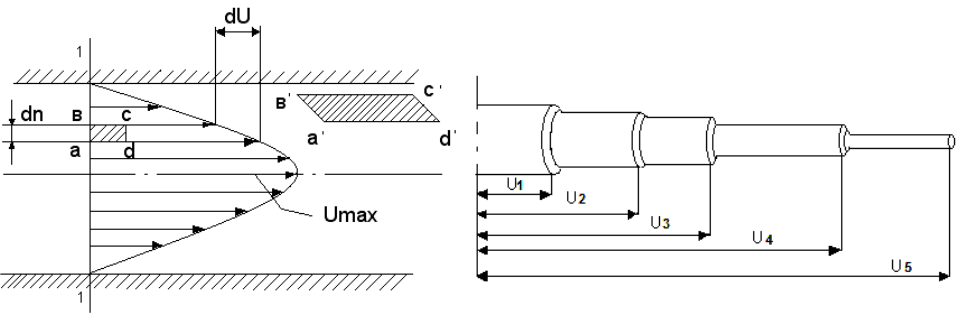
ламинарным и в дальнейшем будет подробно изучено). Скорости

частиц, расположенных в некотором поперечном сечении трубы

1-1, отличаются друг от друга (рис. 2.1).

Скорость жидкости у стенки равна нулю, возрастает по на-

правлению к оси трубы, достигая на оси наибольшего значения

max

. Поток жидкости может быть представлен как движение от-

дельных бесконечно тонких цилиндрических слоев жидкости, пе-

ремещающихся с различными скоростями, увеличивающимися к

оси трубы.

Рис.2.1

Вследствие молекулярного движения молекулы жидкости

пересекают слои жидкости, движущиеся по отношению друг к

другу с относительной скоростью, благодаря чему на поверхно-

сти соприкасающихся слоев жидкости возникают силы трения.

При этом слои жидкости, движущиеся быстрее, увлекают за со-

бой слои, движущиеся медленнее, тормозят движение слоев,

движущихся быстрее. В таком движении частицы жидкости в ви-

де прямоугольника a, b, c, d деформируются в параллелограмм

, c

, d

. Деформация объема является обязательным условием

возникновения сил трения.

Исаак Ньютон в 1687 году сумел установить, что силы внут-

реннего трения, возникающие между соседними движущимися

слоями жидкости, прямо пропорциональны скорости относитель-

ного движения и площади поверхности соприкосновения, вдоль

которых совершается относительное движение, зависят от рода

жидкости и не зависят от давления.

Гипотеза Ньютона подвергалась многократной опытной

проверке и полностью подтвердилась. Чрезвычайно ценные ис-

следования для доказательства этой гипотезы были выполнены

крупнейшим русским ученым, профессором Н.П. Петровым

(1836-1920 гг.), создателем гидродинамической теории смазки.

Гипотеза Ньютона стала законом жидкостного трения. В ма-

тематической форме он выражается следующим образом

T µω=

, (2.11)

где Т – сила внутреннего трения, Н;

– градиент скорости,

имеющий положительный или отрицательный знак в зависимости

от характера изменения скорости по сечению; dU – разность ско-

ростей движения соседних соприкасающихся слоев жидкости в

предположении, что эти слои являются бесконечно тонкими, м/с;

dn – расстояние между осями соседних слоев, м; ω – площадь со-

прикасающихся слоев, м

; µ - динамический коэффициент вязко-

сти, Па·с.

Силу трения Т, отнесенную к единице площади ω, называют

касательным напряжением:

µ=τ

. (2.12)

Жидкости, подчиняющиеся выражениям (2.11) и (2.12), при-

нято называть ньютоновскими.

Наряду с динамической вязкостью µ в гидравлических рас-

четах применяют кинематическую вязкость:

=ν

,м

/с (2.13)

Единицей измерения кинематической вязкости является

стокс 1 Ст = 1 см

/с. Сотая часть стокса называется сантистоксом

(сСт). Приборы для измерения вязкости называются вискозимет-

рами. Динамическую вязкость можно определить ротационными

вискозиметрами.

На практике часто сравнивают время истечения жидкости со

временем истечения воды. Это отношение называют условной

вязкостью (ВУ) и измеряют в градусах Энглера:

воды

жидкости

Е =

. (2.14)

Но величина условной вязкости безразмерна и при решении

задач неудобна, поэтому существуют эмпирические формулы пе-

ресчета. Одна из них

0731

ºЕ -

0631,0

, см

/с (2.15)

В США и Англии получили распространение единицы изме-

рения вязкости в секундах Редвуда (

´´

Re) и Сейболта (

´´

S), во

Франции – градусы Барбье (

В).

Вязкость жидкостей существенным образом зависит от тем-

пературы. Она уменьшается с ее ростом. От увеличения давления

вязкость также зависит, увеличиваясь с его ростом. Причем эта

зависимость для разных температур будет различной.

В пределах относительно небольших давлений (0…40 МПа)

вязкость, например, минеральных масел изменяется с изменени-

ем давления практически линейно (примерно в три раза). В пре-

делах давления 0…150 МПа вязкость повышается в 17 раз,

0…400 МПа – в сотни раз. При давлениях порядка 150…2000

МПа минеральные масла затвердевают.

Кроме ньютоновских жидкостей, существуют жидкости

аномальные (структурные), которые не подчиняются закону

Ньютона, и поэтому их называют неньютоновскими. Это осадки

сточных вод (гели), цементные, глинистые и меловые растворы,

парафинистые нефти вблизи температуры их застывания, разно-

образные коллоидные растворы (белок, крахмал, клей), нефтяные

эмульсии (смеси с водой), суспензии (шламы, гидроторф, озер-

ный ил, битумы), молочные продукты, кормовые смеси, различ-

ного рода пасты.

Перечисленные аномальные жидкости подчиняются закону

Шведова – Бингама

фф +=

, Н/м

(2.16)

где

- начальное напряжение сдвига; µ

′

- структурная вязкость.

Жидкости, подчиняющиеся выражению (2.16), называются

еще бингамовскими, или вязко-пластичными. Для повышения

достоверности расчетов таких жидкостей начальное напряжение

сдвига

, как правило, определяют экспериментально.

3. ГИДРОСТАТИКА

В гидростатике рассматривается жидкость, находящаяся в

общем случае в состоянии относительного покоя, т.е. при отсут-

ствии взаимного перемещения отдельных ее частиц. При этом

жидкость перемещается как твердое тело.

Частным случаем относительного покоя является «абсолют-

ный» покой, под которым подразумевается покой относительно

земли. Приведем несколько примеров.

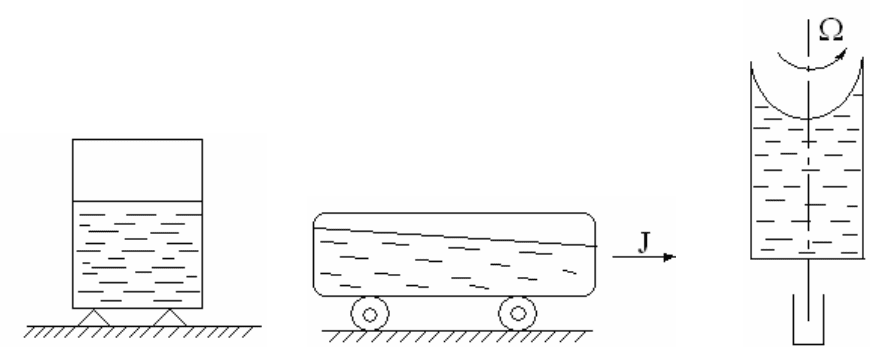
1. Абсолютный покой – жидкость находится в покое в ре-

зервуаре, неподвижном относительно земли (рис. 3.1).

2. Относительный покой: а) жидкость находится в покое от-

носительно железнодорожной цистерны, которая вместе с жидко-

стью движется прямолинейно с некоторым ускорением J

(рис.3.2); б) жидкость находится в покое относительно резервуа-

ра, который вместе с жидкостью вращается с постоянной угловой

скоростью Ω (рис.3.3).

Рис. 3.1

Рис. 3.2

Рис. 3.3

На жидкость, находящуюся в относительном покое, дейст-

вуют массовые силы (сила тяжести и сила инерции переносного

движения), а из поверхностных сил - только силы давления.

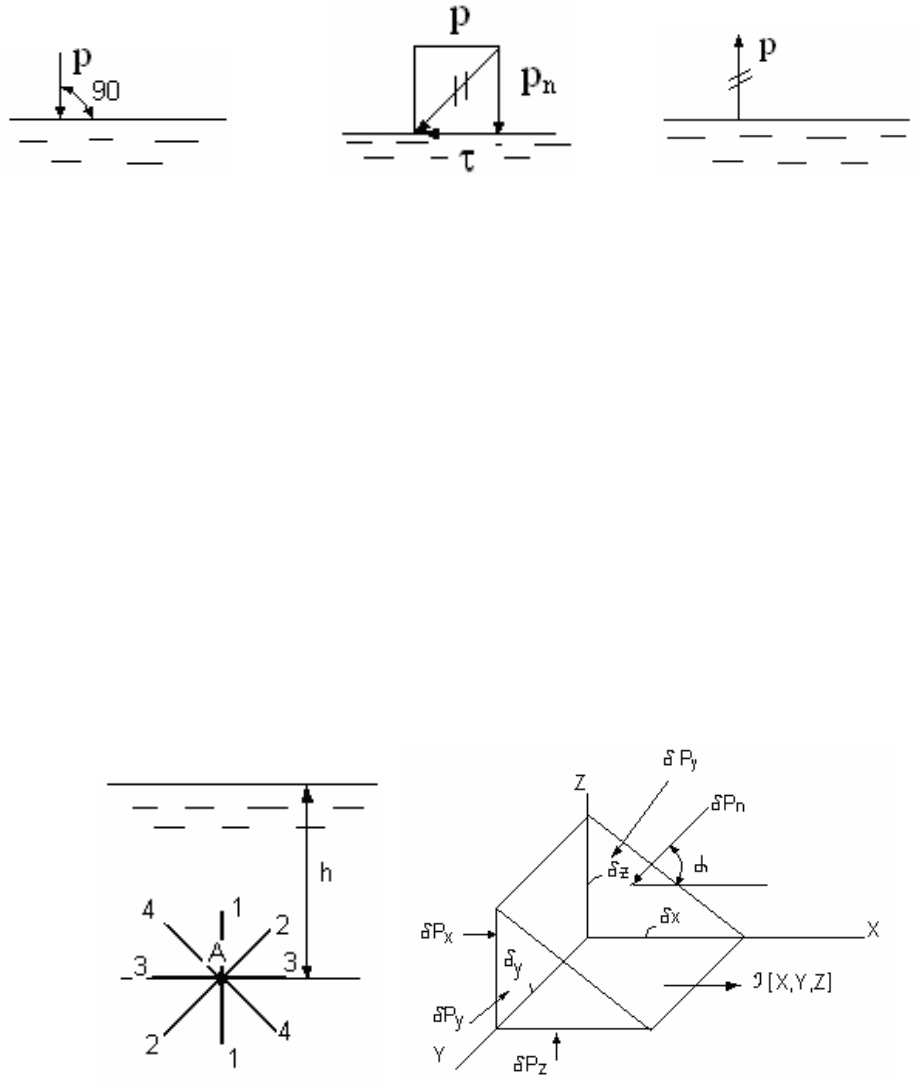
3.1. Свойства гидростатического давления

Гидростатическое давление направлено всегда по внутрен-

ней нормали к площадке, на которую оно действует (рис.3.4).

Доказательство ведется от обратного утверждения.

Рис.3.4

Рис.3.5

Рис. 3.6

Допустим, гидростатическое давление направлено не по

нормали к площадке (рис.3.5). В этом случае его можно разло-

жить на нормальную р

и касательную составляющие τ. Появле-

ние касательной составляющей станет нарушением условия отно-

сительного покоя, т.е. частицы жидкости якобы будут переме-

щаться друг относительно друга.

Допустим, гидростатическое давление направлено по внеш-

ней нормали к площадке (рис.3.6). Это значило бы, что жидкость

сопротивляется растягивающим усилиями, что нарушило бы

принятую ранее аксиому.

Гидростатическое давление в любой точке покоящейся жид-

кости не зависит от направления площадки, для которой оно вы-

числено.

Рис. 3.7 Рис. 3.8

Проиллюстрируем это свойство. В жидкости на глубине h

мысленно возьмем точку А (рис.3.7). Можно предположить, что

давление в этой точке будет совершенно одинаковым для на-

правления площадок 1-1, 2-2, 3-3 и т.д., проходящих через эту

точку. Докажем это очевидное свойство.

Для этого в жидкости, находящейся в покое, разместим оси

координат и выделим в этих осях элементарный объем в виде

прямоугольного клина (рис.3.8), стороны граней которого по

осям равны δх, δу, δz. Применим принцип отвердевания, т.е.

мысленно представим, что бесконечно малый объем превратился

в твердое тело. В этом случае при рассмотрении тела в покое

можно применить законы механики твердого тела, т.е. если тело

находится в равновесии (покое), то сумма проекций всех сил на

соответствующие оси равна нулю, т.е. ΣP

= 0, ΣP

= 0.

На выделенный объем действуют массовая сила, вызванная

ускорением J, проекции которого на соответствующие оси будут

равны X, Y, Z, и поверхностные силы на соответствующие грани

δP

, δP

. Направление грани с индексом «n» в системе

координат взято произвольно.

Составим уравнение проекции сил на ось Х:

ΣР

= δР

- δР

·cosα + ХδМ = 0. (3.1)

Ввиду малости размеров граней клина будем считать, что

давление на каждую из них будет одинаковым и каким-то сред-

ним, тогда

дxдyдz

Xс

cos

дyдz

cosб

n ср

рдyдz

xср

=+−

Сократив на δу·δz, получим:

0Xссд

n ср

хср

=+−

В пределе, когда размеры клина будут приближаться к нулю,

ср x

и р

ср n

будут стремиться к значениям гидростатического дав-

ления в точке в направлениях оси Х-Р

и наклонной грани n – P

и вследствие этого при переходе к пределу при δх = 0 получаем:

– р

= 0 или р

= р

Составив уравнение проекции сил на оси y и z, найдем, что

= р

; р

= р

, откуда

= P

. (3.2)

Последнее равенствопоказывает, что гидростатическое дав-

ление в точке покоящейся жидкости имеет значение, не завися-

щее от направления площадки, для которой оно вычислено.

Но гидростатическое давление в различных точках не будет

одинаковым. Для разных точек давление будет являться непре-

рывной функцией координат.

3.2. Дифференциальные уравнения равновесия жидкости

(уравнения Леонарда Эйлера)

Целью вывода этих уравнений будет ответ на вопрос: каки-

ми по своей природе должны быть силы, под действием которых

жидкость будет находиться в равновесии? Для вывода этих урав-

нений в жидкости, находящейся в покое, условно разместим сис-

тему координат и выделим элементарный объем в виде прямо-

угольного параллелепипеда с ребрами δx, δy, δz (рис.3.9).

Рис.3.9

Применим принцип отвердевания. В этом случае при рас-

смотрении тела в покое можно применить законы механики твер-

дого тела, т.е. если тело находится в равновесии, то сумма проек-

ций всех сил на соответствующие оси равна нулю:

ΣР

= 0; ΣР

= 0. (3.3)

На выделенный объем действует массовая сила, вызванная

ускорением J, проекции которого на соответствующие оси будут

равны X,Y,Z, и поверхностные силы δР

Рассмотрим условие равновесия по оси Х. Допустим, на ле-

вую грань параллелепипеда действует элементарная сила δР

, на

правую δР

ΣР

= δР

-δР

+ХδМ=0. (3.4)

Ввиду малости размеров граней параллелепипеда будем счи-

тать, что давление на каждую из них будет одинаковым и каким-

то средним, тогда

дz

дy

дx

дz

дy

дz

дy

ср

⋅

−

⋅

(3.5)

Выразим давления

ср

через давление р в центре па-

раллелепипеда.

Так как жидкость является сплошной средой (т.е. средой без

пустот и переуплотнений), то изменение давления на каком-то

элементарном перемещении является непрерывной функции ко-

ординат:











∂

−=

дx

ср

дx

ср

, (3.6)

где

∂

- градиент гидростатического давления, т.е. частная про-

изводная от давления по оси Х.

Подставим выражение (3.6) в (3.5)6

0zyxXzy

pzy

p =δδρδ+δδ













∂

+−δδ













∂

−

Сократим на δх·δу·δz, т.е. на объем δW, и переходя к преде-

лу:

=ρ+

∂

−

. (3.7)

Аналогично рассуждая, но проектируя силы на оси Y и Z,

получим еще два уравнения равновесия.

Общепринятая форма записи этих уравнений выглядит так:











∂

−

∂

−

∂

−

(3.8)

Уравнения (3.8) представляют собой общие дифференциаль-

ные уравнения равновесия жидкости, из которых следует, что при

перемещении в жидкости давление зависит от плотности и уско-

рения.

Для лучшего понимания смысла полученных уравнений и

практического пользования удобнее вместо системы уравнений

(3.8) получить одно эквивалентное им уравнение. Для этого ле-

вую и правую части уравнений умножим соответственно на dx,

dу, dz и сложим













∂

=++ dz

ZdzYdyXdx

, (3.9)

где

dy;

dx;

∂

- частные дифференциалы давления; они по

соответствующим осям определяют изменение (увеличение или

уменьшение) давления при переходе на расстояние dx, dy, dz.

Так как гидростатическое давление есть функция только ко-

ординат, выражение в скобках уравнения (3.9) представляет со-

бой полный дифференциал гидростатического давления:

∂

. (3.10)

В связи с этим получим одно дифференциальное уравнение

для жидкости, находящейся в относительном покое:

(

)

ZdzYdyXdxdp

. (3.11)

Плотность жидкости ρ в уравнении (3.11) можно принять

постоянной величиной, поэтому уравнение (3.11) может иметь

смысл только в том случае, если его правая часть также является

полным дифференциалом. Для этого необходимо, чтобы сущест-

вовала некая функция U = f(Х,Y,Z), частные производные кото-

рой по осям x,y,z были бы равны:

∂

Такая функция называется потенциальной, или силовой, а

силы, которые этой функцией выражаются – силами, имеющими

потенциал.

Следовательно, жидкость находится в равновесии под дей-

ствием сил, имеющих потенциал. Из механики известны многие