Презентация - Загиров Н.Н., Иванов Е.В. Механика сплошных сред. Теория обработки металлов давлением
Подождите немного. Документ загружается.


Задача Задача –– построить эпюру нормальных напряжений, построить эпюру нормальных напряжений,
действующих на контактной поверхности.действующих на контактной поверхности.
Запишем Запишем систему дифференциальных уравнений систему дифференциальных уравнений
теории пластичноститеории пластичности::
1. 1. Дифференциальные уравнения равновесия Дифференциальные уравнения равновесия
(с учетом того, что (с учетом того, что σσ
xyxy
= = σσ
yxyx
) упростятся:) упростятся:
0=
∂
σ
∂
+
∂
σ∂
y
xy
x
xx
0=
∂
σ
∂
+
∂
σ
∂
y
yy
x
xy
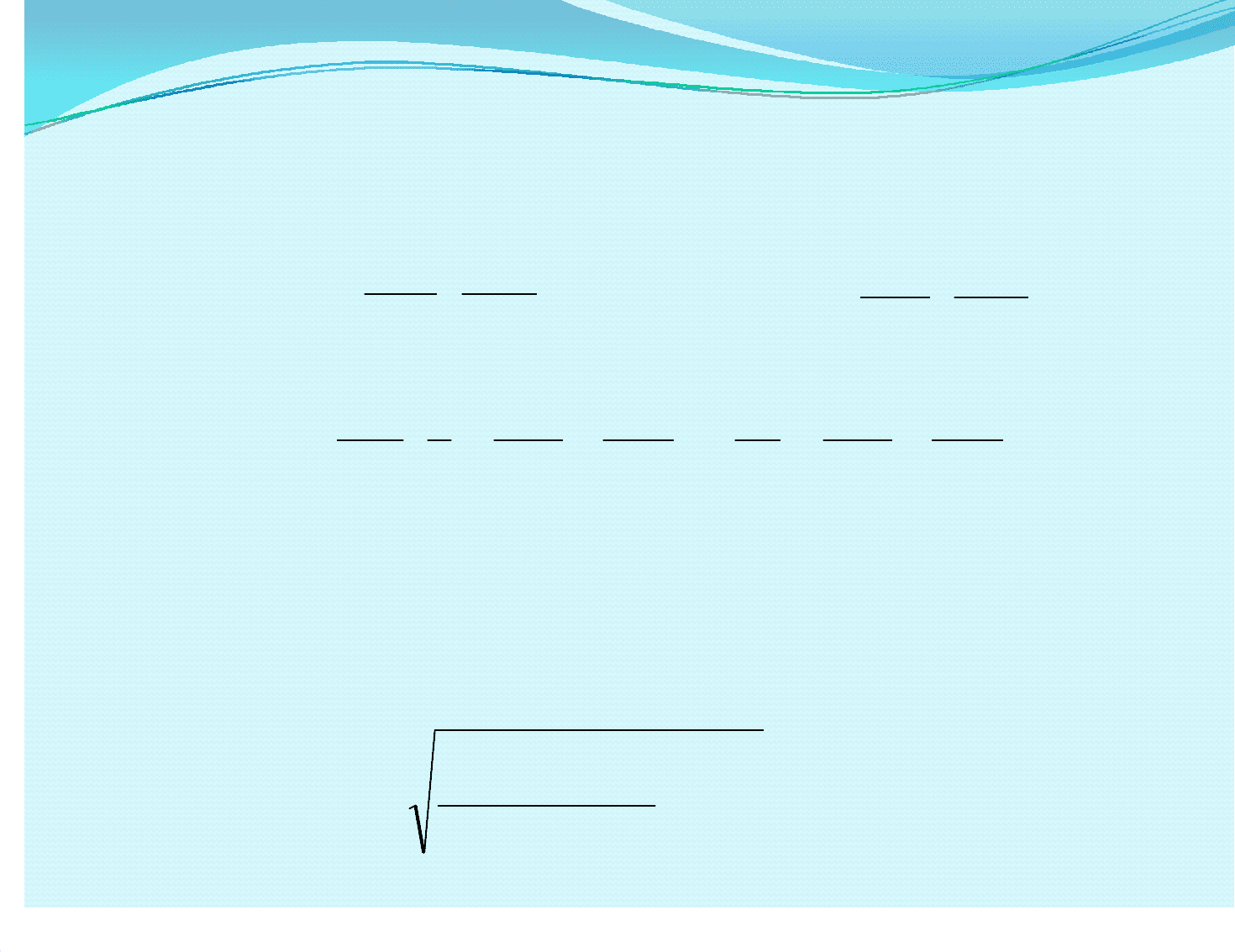
2. 2. Физические уравнения связи напряжений и Физические уравнения связи напряжений и
деформаций (при деформаций (при ТТ = = ττ
SS
) преобразуются к виду) преобразуются к виду
x
H
xS
xx
∂
ϑ
∂
⋅
τ
=σ−σ
2
yH
y
S
yy
∂
ϑ
∂
⋅
τ
=σ−σ
2
∂
ϑ∂
+
∂
ϑ∂
⋅
τ
=
∂
ϑ∂
+
∂
ϑ∂
⋅⋅
τ
=σ
xyHxyH
y
xS
y
xS
xy
2
1
2
из первого уравнения вычитают второе, из первого уравнения вычитают второе,
возводят оба оставшихся уравнения в квадрат возводят оба оставшихся уравнения в квадрат
и складывают их:и складывают их:
(
)
Sxy
yyxx
τ=σ+
σ−σ
2
2
4

из первого уравнения вычитают второе и делят из первого уравнения вычитают второе и делят
на третье:на третье:
xy
yx
y
x
y
x
xy
yyxx
∂
ϑ∂
+
∂
ϑ∂
∂
ϑ
∂
−
∂
ϑ∂
=
σ
σ−σ
2
3.3. Условие несжимаемости примет видУсловие несжимаемости примет вид
0=
∂
ϑ
∂
+
∂
ϑ∂
yx
y
x

Сформулируем граничные условия:Сформулируем граничные условия:
При При xx= = bb ;;
0
=
σ
=bxxx
0=σ
=bxxy
при при yy= = hh
ϑ−=ϑ
=hyy
при при yy= = ––hh
ϑ=ϑ
−= hyy
Предположим, что рассматривается случай, Предположим, что рассматривается случай,
когда на контакте действуют максимальные когда на контакте действуют максимальные
касательные напряжения (касательные напряжения (ττ = = ττ
SS
), тогда), тогда
Shyxy
τ−=σ
=
Shyxy
τ=σ
−=
;;
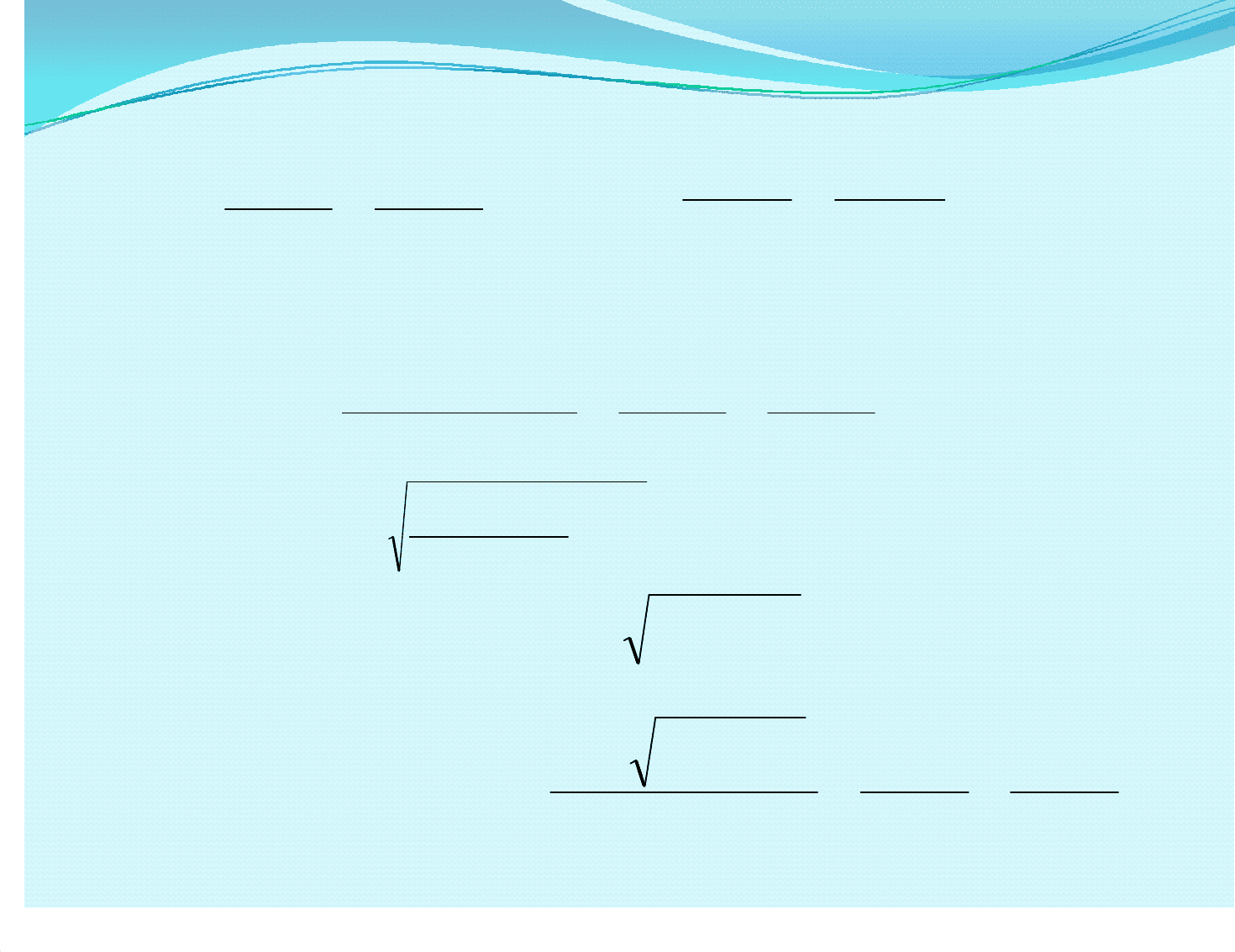
Продифференцируем уравнения равновесия по Продифференцируем уравнения равновесия по
переменным переменным yy ии xx соответственно соответственно
0
2
2
2
=
∂
σ∂
+
∂∂
σ∂
y
yx
xy
xx
0
2
2
2
=
∂∂
σ∂
+
∂
σ∂
xy
x
yyxy
;;
Вычитаем из первого уравнения второе:Вычитаем из первого уравнения второе:
(
)
0
2
2
2
22
=
∂
σ∂
−
∂
σ∂
+
∂∂
σ−σ∂
xy
yx
xyxyyyxx
Из уравнения определяем разность:Из уравнения определяем разность:
(
)
Sxy
yyxx
τ=σ+
σ−σ
2
2
4
22
2
xySyyxx
σ−τ=σ−σ
и подставляем в (1) :и подставляем в (1) :
(1)(1)
(
)
0
2
2
2
2
2
222
=
∂
σ∂
−
∂
σ∂
+
∂∂
σ−τ∂
xy
yx
xyxy
xyS

Предположим, что Предположим, что σσ
xyxy
, действующая внутри тела, , действующая внутри тела,
не является функцией от не является функцией от xx, т.е. , т.е. σσ
xyxy
≠≠ ff((xx), тогда), тогда
0
2
2
=
∂
σ∂
y
xy
Осуществим интегрирование выраженияОсуществим интегрирование выражения
()
xf
y
xy
1
=
∂
∂σ
в результате получим:в результате получим: σ
xy
= f
1
(x) ⋅ y + f
2
(x), (2)
где fгде f
11
, f, f
22
–– произвольные функции интегрирования, произвольные функции интегрирования,
которые находятся из граничных условий:которые находятся из граничных условий:
–τ
S
= f
1
(x)⋅h + f
2
(x);
τ
S
= –f
1
(x)⋅h + f
2
(x).
Если их сложить, то Если их сложить, то ff
22
((xx) = 0) = 0, а если вычесть, то , а если вычесть, то ff
11
((xx) = ) = ––ττ
SS
/ / hh..

После подстановки в После подстановки в (2)(2) имеемимеем
σ
xy
= –τ
S
⋅ y / h.
Подставляем в первое дифференциальное Подставляем в первое дифференциальное
уравнение равновесия, находимуравнение равновесия, находим
0=
τ
−
∂
∂σ
h
x
Sxx
⇒
()
yx
h
S
xx 1
ϕ+
τ
=σ
,,
а подставив во второе дифференциальное а подставив во второе дифференциальное
уравнение равновесия, имеемуравнение равновесия, имеем
0=
∂
∂σ
y
yy
σ
yy
= ϕ
2
(x).
⇒
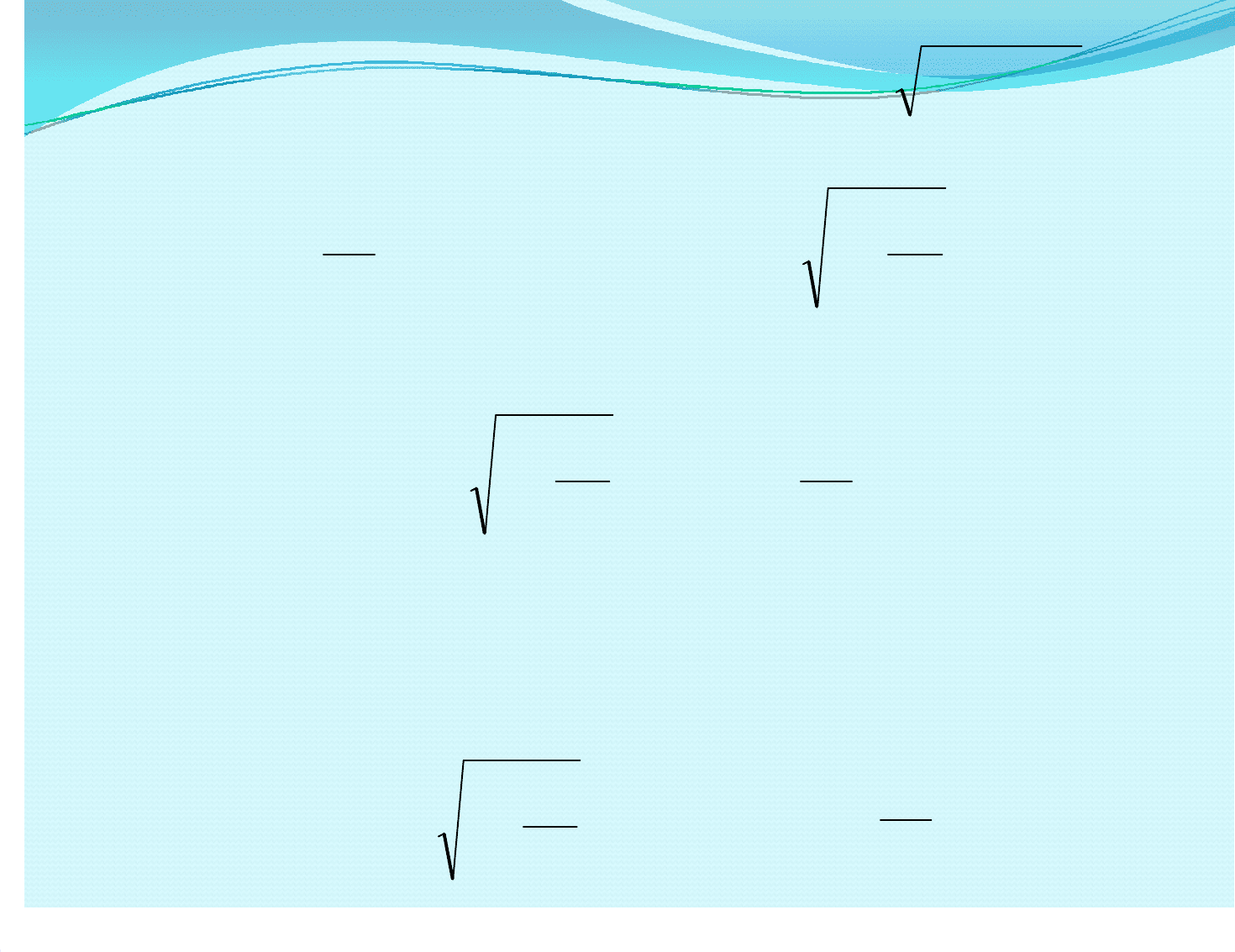
Подставив в выражениеПодставив в выражение
22
2
xySyyxx
σ−τ=σ−σ
составляющие составляющие σσ
хххх
,, σσ
yyyy
и и σσ
хyхy
, получим, получим
() ()
2
2
21
12
h
y
xyx
h
S
S
−τ=ϕ−ϕ+
τ
..
Разделяем члены с одинаковыми переменными:Разделяем члены с одинаковыми переменными:
() ()
Cx
h
x
h
y
y
S
S
=
τ
−ϕ=−τ−ϕ
2
2
2
1
12
,,
где где СС –– некоторая постоянная величина.некоторая постоянная величина.
Приравняв отдельно правую и левую части Приравняв отдельно правую и левую части
постоянной постоянной СС, найдем, найдем
()
C
h
y
y
S
+−τ=ϕ
2
2
1
12
;;
()
Cx
h
x
S
+
τ
=ϕ
2
..
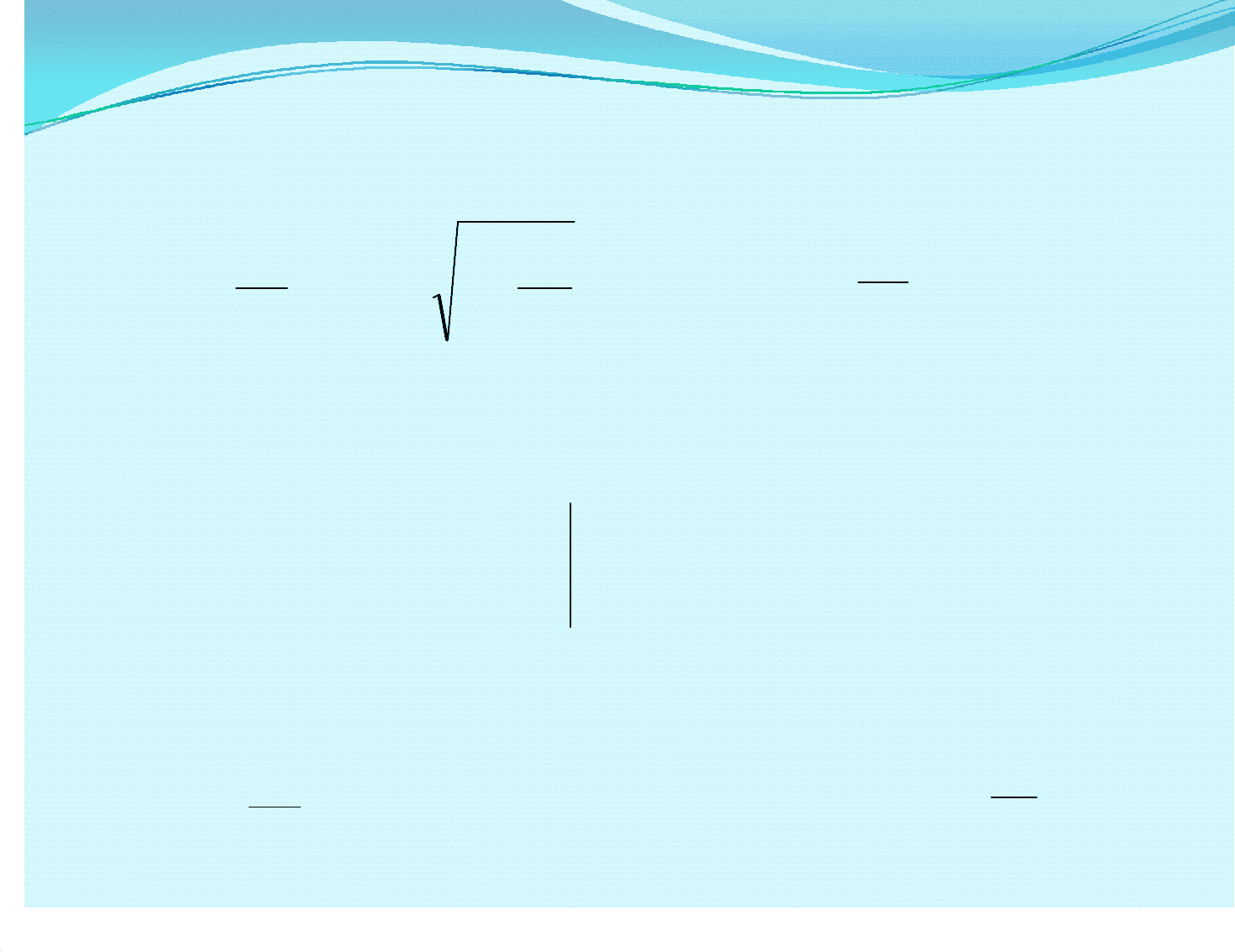
После подстановки функций После подстановки функций ϕϕ
11
((yy) ) и и ϕϕ
22
((xx) в ) в
выражения для выражения для σσ
xxxx
и и σσ
yyyy
имеемимеем
C
h
y
x
h
S
S
xx
+−τ+
τ
=σ
2
2
12
Cx
h
S
yy
+
τ
=σ
;;
Постоянную интегрирования Постоянную интегрирования СС найдем, найдем,
используя граничное условиеиспользуя граничное условие
0
0
=σ
=
=
y
bxxx
Подставив его в формулу для нахождения Подставив его в формулу для нахождения σσ
xxxx
, получим, получим
Cb
h
S
S
+τ+
τ
= 20
отсюдаотсюда
b
h
C
S
S
τ
−τ−= 2
В итогеВ итоге
−
⋅τ−τ⋅−=σ
−τ+
−
τ−τ−=σ
h
xb
h
y
h
xb
SSyy
SSSxx
2
122
2
2
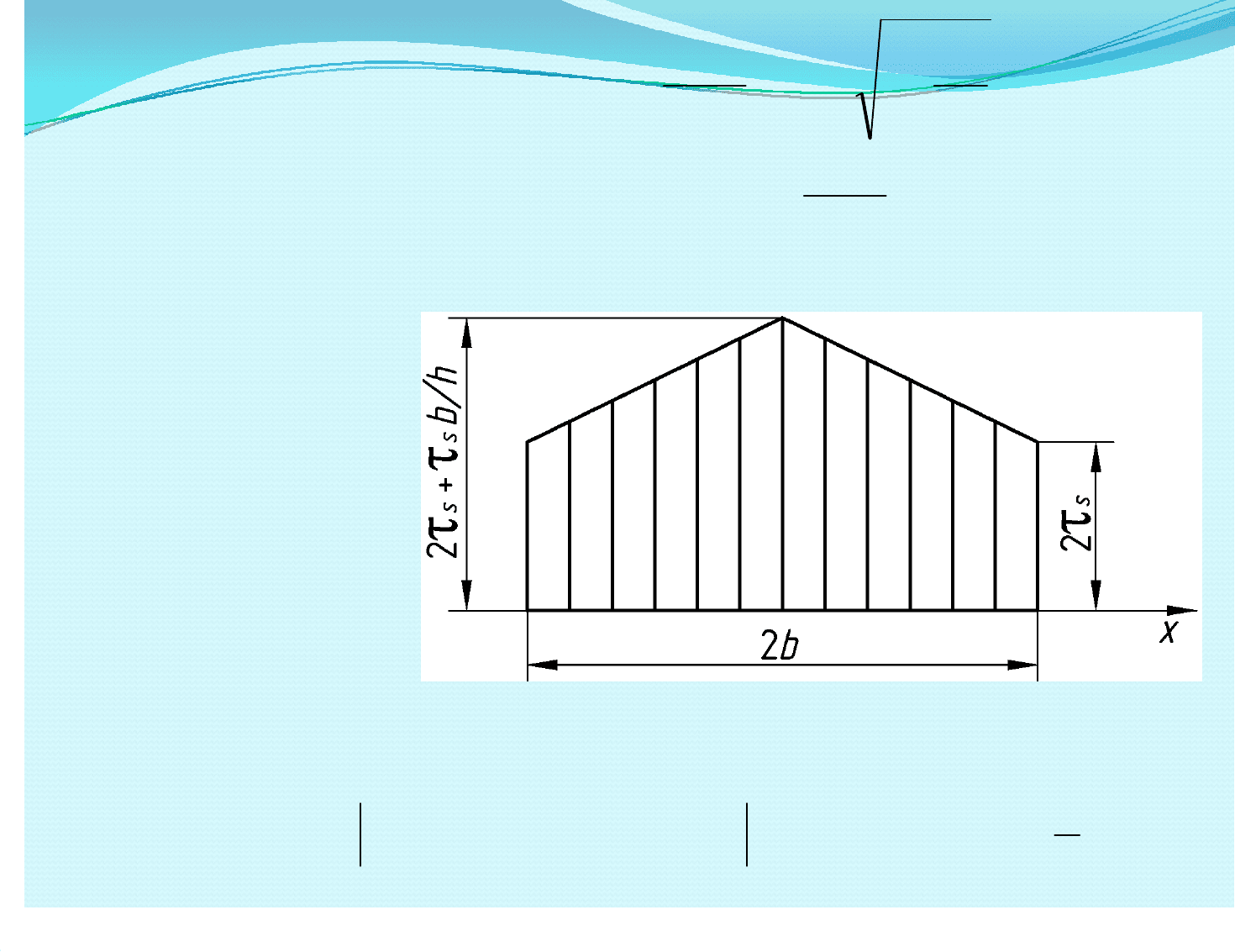
Эпюра нормальных Эпюра нормальных
напряжений, напряжений,
действующих надействующих на
контактной контактной
поверхности,поверхности,
рис. 37.2.
эпюра имеет две характерные точки:эпюра имеет две характерные точки:
Syy
bx
τ−=
=
σ 2
h
b
x
SSyy
τ−τ−=
=
σ 2
0
;;
