Power electronic handbook

Подождите немного. Документ загружается.

886 M. F. Rahman et al.

in the rotor and by having three-phase windings in the stator

that are supplied from an inverter.

The arrangement just mentioned is very similar to a con-

ventional synchronous motor. This is particularly so when the

stator windings and the rotor mmf are sinusoidally distributed.

Several rotor conﬁgurations of the PM synchronous motor

have been developed, of which the important ones are

indicated in Figs. 33.45–33.47.

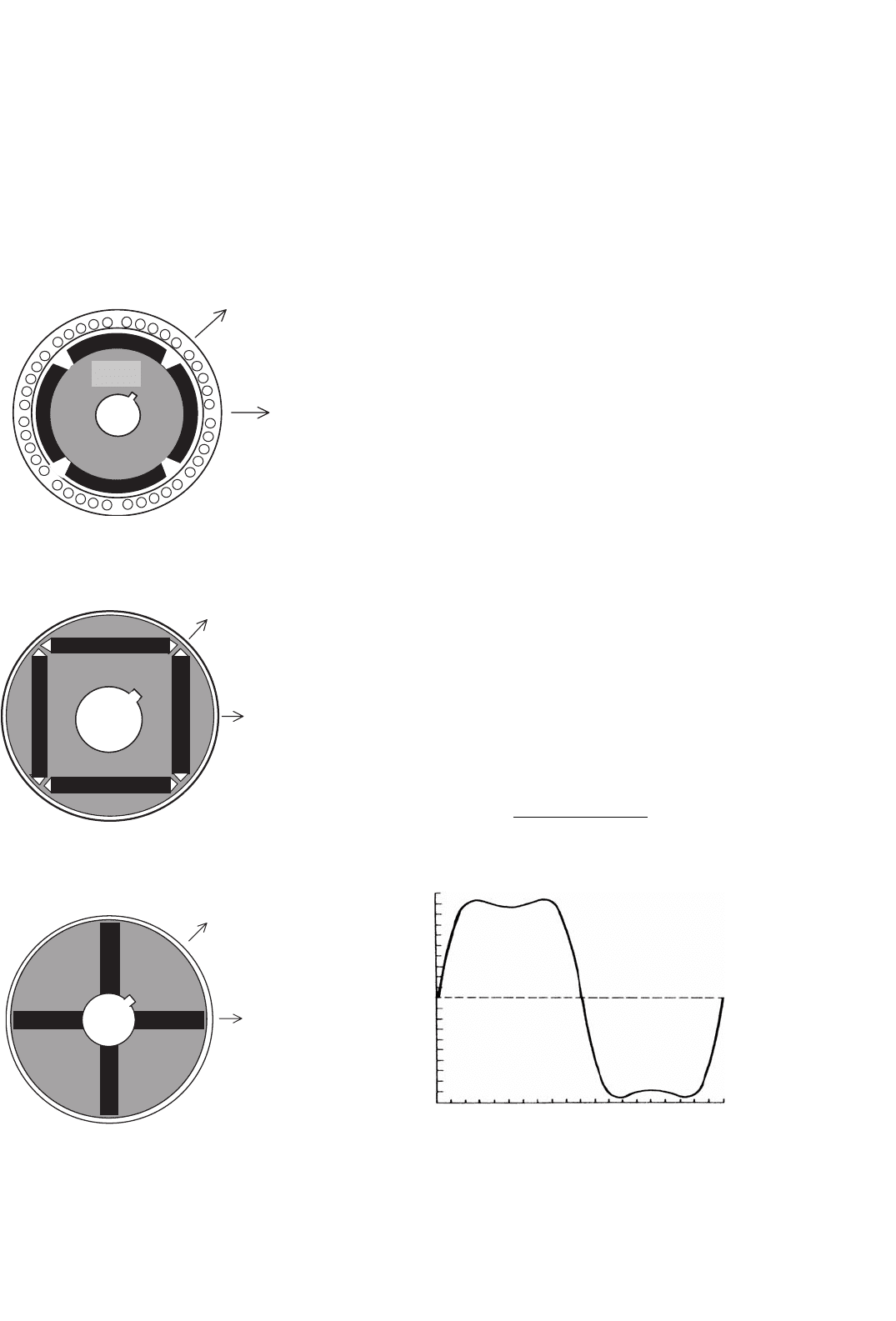
rotor

q-axis

d-axis

FIGURE 33.45 Schematic of the cross section of a surface-magnet

synchronous motor.

q -axis

d -axis

FIGURE 33.46 Schematic of the rotor cross section of an interior-

magnet motor.

d -axis

q-axis

FIGURE 33.47 Schematic of the rotor cross section of a circumferential-

magnet motor.

33.5.2 The Surface-magnet Synchronous Motor

The surface-magnet motor comes with the rotor magnets

glued onto the surface of the rotor. An additional stainless steel

(i.e. nonmagnetic) cylindrical shell may be used to cover the

rotor in order to keep the magnets in place against centrifugal

force in high-speed applications. Since the relative permeabil-

ity of the magnetic material is very close to unity, the effective

airgap is uniform and large. The airgap is normally about

8 mm. Consequently, the synchronous inductances along the

rotor d- and q-axes, as indicated in Fig. 33.45, are equal and

small (i.e. L

= L

). The armature reaction in this type

of motor is small.

The three-phase winding in the stator has sinusoidal dis-

tributed windings. In another form, the motor may have

trapezoidal distributed winding, and the rotor mmf is also

uniformly distributed. Such a motor, often called a brushless

dc (BLDC) motor because of its similarity to the inside-out

conventional brushed PM DC motor, develops a trapezoidal

back-emf waveform as indicated in Fig. 33.48, when it is driven

at a constant speed. The back-emf waveforms have ﬂat tops

for nearly 120

◦

in each half-cycle followed by 60

◦

of transition

from positive to negative polarity of voltage and vice versa.

These motors are very suitable for variable-speed applications

such as spindle drives in machine-tool and disk drives.

33.5.2.1 Control of the Trapezoidal-wave Motor

Neglecting higher-order harmonic terms, the back-emf in the

motor phases may be as indicated in Fig. 33.49. Each back-

emf has a constant amplitude (or ﬂat top) for 120

◦

(electrical)

followed by 60

◦

of transition in each half-cycle. The developed

torque at any instant is given by

T =

Nm (33.71)

EMF, V

−18

−36

0 90 180

θ, degree

270 360

FIGURE 33.48 Back-emf of a trapezoidal waveform motor.

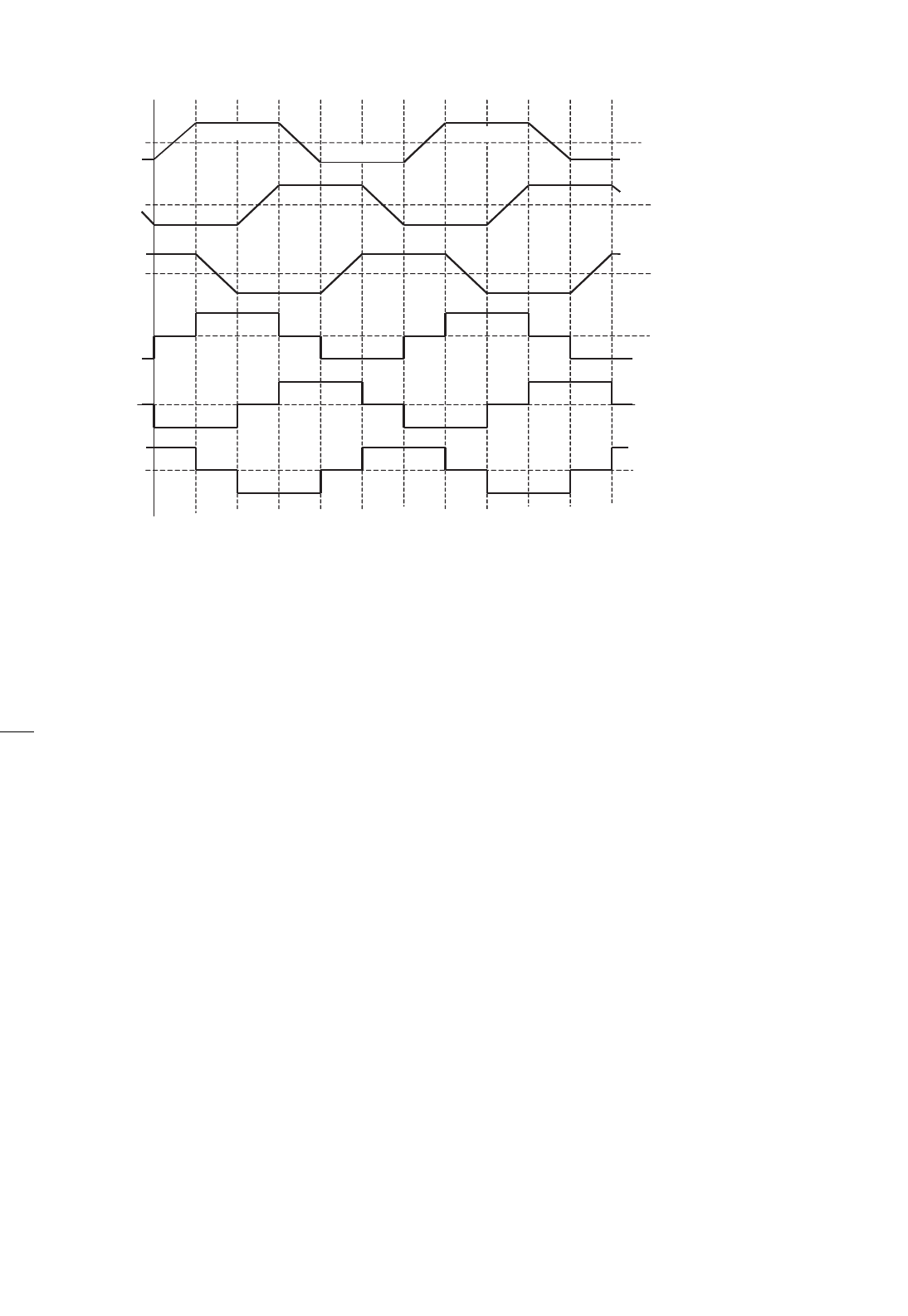
33 Motor Drives 887

1261

23 34

4534

1261

56 56

60°

60° 60°

60°

120°

FIGURE 33.49 Back-emf and current waveforms and on-states of transistor switches in the trapezoidal-waveform motor.

It is readily seen that the ideal current waveform in each

phase needs to be a quasi-square waveform of 120

◦

of con-

duction angle in each half-cycle. The conduction of current in

each phase winding coincides with the ﬂat part of the back-emf

waveforms, which guarantees that the developed torque, i.e.





x=a

·i



, is constant or ripple-free at all times. With such

quasi-square current waveforms, a simple set of six opto-

couplers or Hall-effect sensors would be required to drive the

six inverter switches indicated in Fig. 33.36. The output cur-

rent waveforms for the three-phase inverter and the switching

devices that conduct during the six switching intervals per

cycle are also indicated in Fig. 33.49. Since only six discrete

outputs per electrical cycle are required from the rotor posi-

tion sensors, the requirement of a high-resolution position

sensor is dispensed with. Continuous current control for each

phase of the motor, by hysteresis or PWM control, to regulate

the amplitude of the motor current in each phase is normally

employed. The operation of the BLDC motor drive is described

in detail in Section 33.6.

Even though careful electromagnetic design is employed in

order to have perfect trapezoidal back-emf waveforms as indi-

cated in Fig. 33.49, the back-emf waveforms in a practical

brushless dc motor exhibit some harmonics, as indicated in

Fig. 33.48. If ripples in the back-emf waveforms are signif-

icant, then torque ripples will also exist when the motor is

driven with quasi-square phase current waveforms. These rip-

ples may become troublesome when the motor is operated at

low speed, when the motor load inertia may not ﬁlter out the

torque ripples adequately.

A second source of torque ripple in the permanent-magnet

brushless dc (PM BLDC) motor is from the commutation of

current in the inverter. Since the actual phase currents cannot

have the abrupt rise and fall times as indicated in Fig. 33.49,

torque spikes, one for each switching, may exist.

Even though the PM BLDC motor does not have sinusoidal

back-emf and inductance variations with rotor angle, the anal-

ysis of Section 33.4 in terms of the fundamental quantities

will often sufﬁce. The switching of the inverter using the six

rotor-position sensors guarantees that the current waveform in

each phase always remains in synchronism with the back-emf

of the respective phase. Since the quasi-square phase current

waveform in each phase coincides with the ﬂat part of the

back-emf waveform of the same phase, the angle γ is clearly

zero for such operation. Thus, considering fundamental quan-

tities, the motor back-emf and the torque characteristics can

be expressed by

E = K

ω V (33.72)

T = K

I cos γ = K

I Nm (33.73)

where K

and K

are equal in consistent units. Note that E

and I are now RMS values of the fundamental components of

these quantities.

888 M. F. Rahman et al.

33.5.2.2 Sensorless Operation of the PM BLDC Motor

In spindle and other variable-speed drive applications, where

the lowest speed of operation is not less than a few hundred

revs/min, it may be possible to obtain the switching signals for

the inverter from the motor back-emf, thus dispensing with

rotor-position sensors. The method consists of integrating the

back-emf waveforms, which are the same as the applied phase

voltage if the other voltage drops are neglected, and comparing

the integrated outputs with a ﬁxed reference. These compara-

tor outputs determine the switching signals for inverter. It

may be noted that the amplitude of the back-emf waveforms

is proportional to the operating speed, so that the frequency

of the comparator outputs increases automatically with speed.

In other words, the angle γ and the current waveform rel-

ative to the back-emf waveform in each phase remains the

same regardless of the operating speed. Integrated circuits are

available from several suppliers, that perform this task of sen-

sorless BLDC operation satisfactorily, covering a reasonable

speed range.

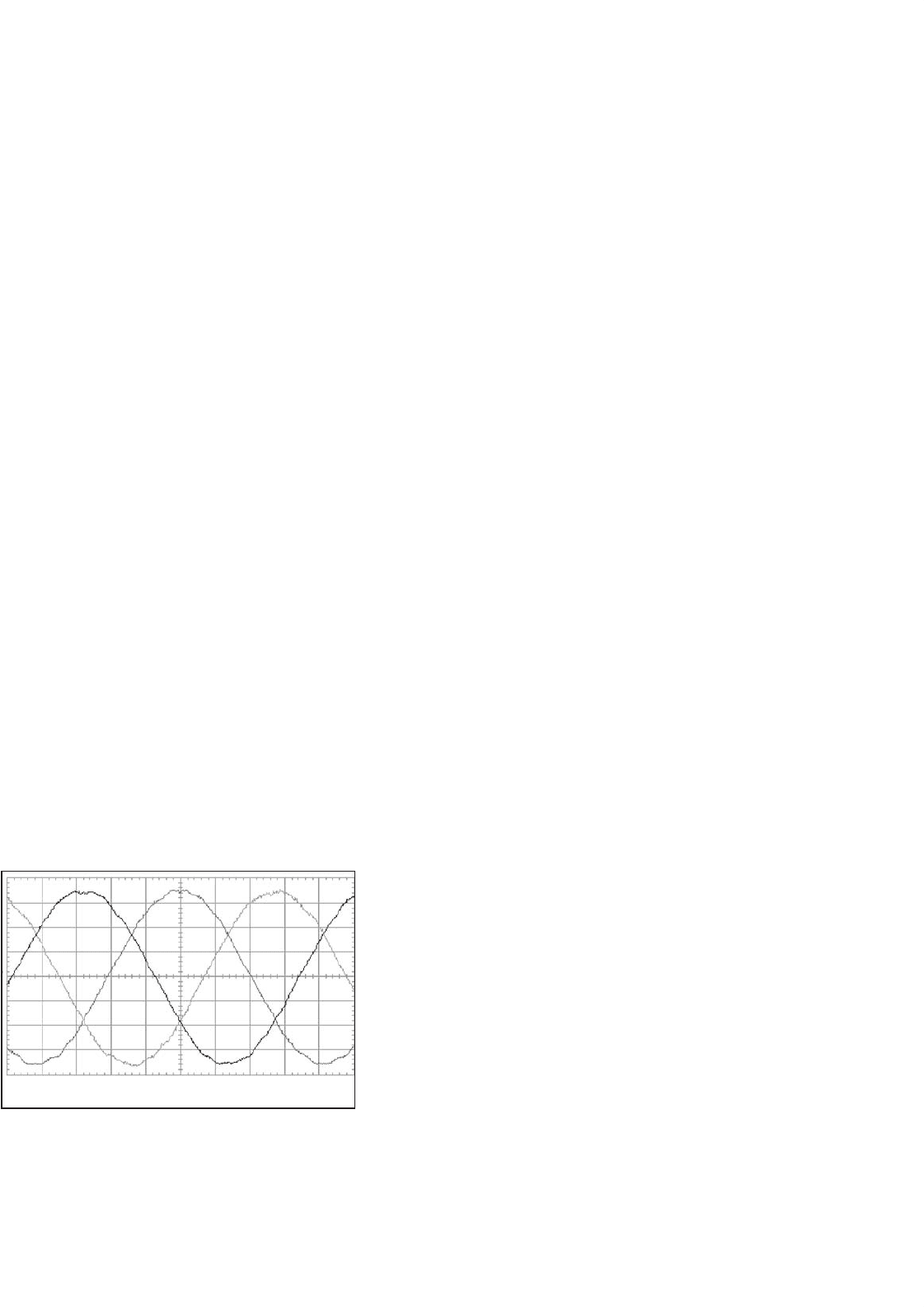
33.5.3 The PM Sinewave Motor

The PM sinewave motor, which may also have magnets on the

rotor surface or buried inside the rotor (as in the interior-

magnet motor of Fig. 33.46), has sinusoidally distributed

windings. The airgap ﬂux distribution produced by the rotor

magnets is also sinusoidal, arranged through magnet shaping.

Consequently, the back-emf waveform of each phase is also

a sinusoidal waveform, as indicated in Fig. 33.50, when the

motor is driven at a constant speed.

It should be noted, however, that with magnets mounted

on the rotor surface, the effective airgap is large and uniform

so that L

= L

. Because of the large equivalent air-

gap, these inductances are also small, and consequently, the

armature reaction is small. As a result, this motor essentially

operates with ﬁxed excitation, and there is hardly any scope

100 V/div 5 ms/div

FIGURE 33.50 Back-emf waveforms of a sinewave PM motor.

Speed = 1815 rev/min.

for altering the operating power factor or the rotor mmf, once

the motor and its drive voltage and current ratings have been

selected.

The PM sinewave interior-magnet motor, which comes with

magnets buried inside the rotor as indicated in Figs. 33.46 and

33.47, has an easier magnetization path along the rotor q-axis,

so that L

> L

. The small airgap implies that the inductances

and L

may not be small, and hence may allow considerable

scope for ﬁeld weakening.

If the sinewave motor is supplied from an SPWM inverter,

the analyses and vector diagrams of this motor are not different

from those in Section 33.4 for the nonsalient-pole and salient-

pole synchronous motor drives. The surface-magnet motor is

more akin to the nonsalient-pole motor, since L

= L

whereas the interior-magnet motor is more akin to the salient-

pole motor because of the d- and q-axes inductances being

unequal. Thus, the equations in Section 33.4 will apply equally

well for this motor, both in the steady state and dynamically

and for both voltage- and current-source supply.

33.5.3.1 Control of the PM Sinewave Motor

The sinusoidal back-emf waveforms imply that the three-phase

motor must be supplied with a sinusoidal three-phase currents

if a dc-motor-like (or vector-control-like) torque characteristic

is desired, as was found in Section 33.4. For such operation, the

phase currents must also be synchronized with the respective

phase back-emf waveforms, in other words, with the rotor dq-

reference frame. This implies the operation with a speciﬁed γ

angle. Two implementations are possible.

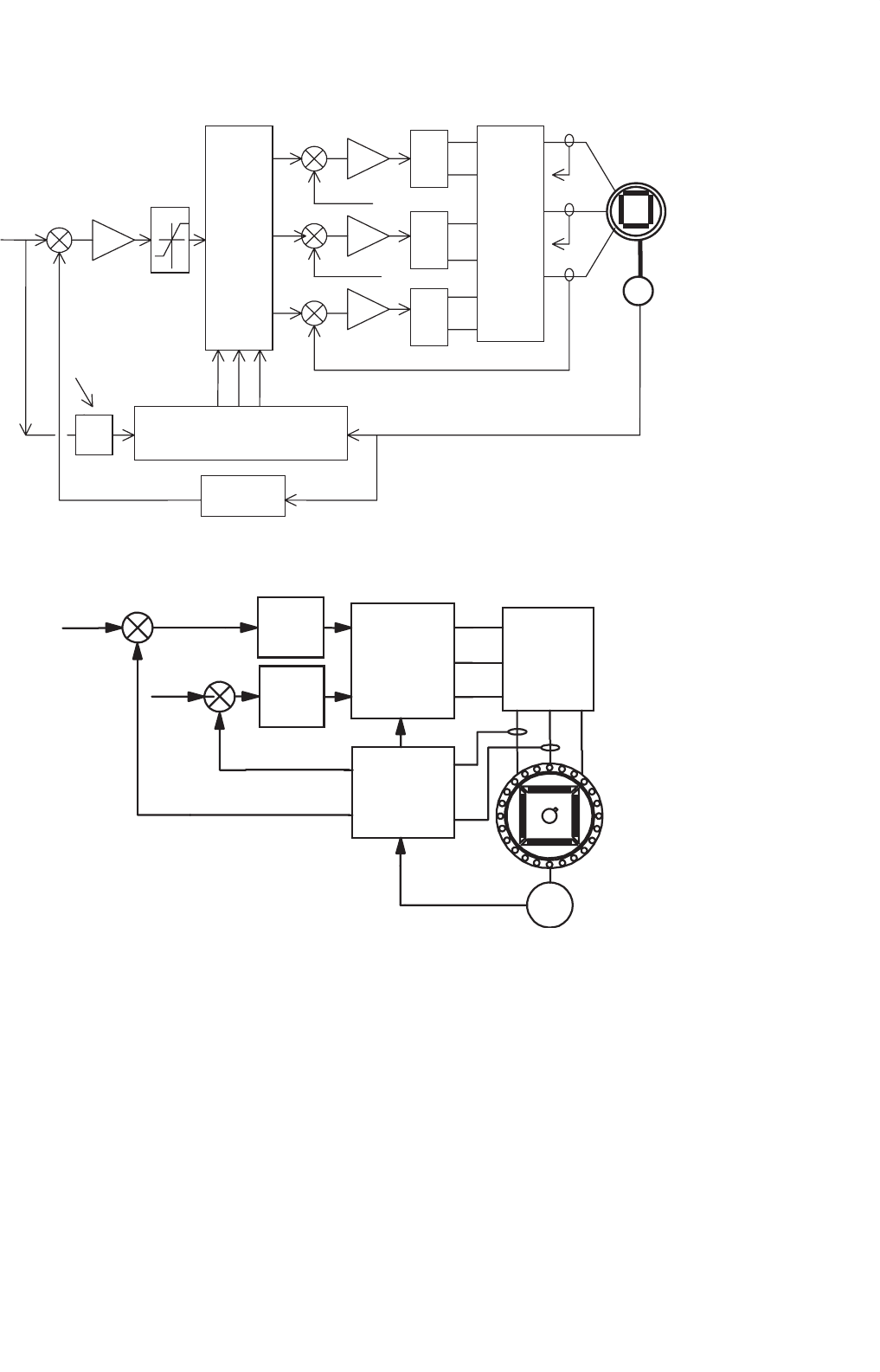
In one scheme, the stator currents are regulated in the stator

reference frame and the stator current references are produced

with reference to the rotor position, as indicated in Fig. 33.51.

The rotor position θ is continuously sensed and used to pro-

duce three sinusoidal current references of unit amplitude.

The phase angle γ of the references relative to the respec-

tive back-emf waveforms is usually derived from the speed

controller, which deﬁnes the ﬁeld-weakening regime of the

drive. The operating power factor of the drive may also be

addressed using the γ angle control, as explained in Section

33.4.5. The amplitudes of these references are then multiplied

by the error of the speed controller in order to produce the

desired torque reference. In this way, both the RMS value I

of the phase current and its angle γ with respect to E

can be

adjusted independently (which is equivalent to independent

dq-axes current control). Three PWM current controllers are

indicated, but two sufﬁce for a balanced motor. Other types of

current controllers, such as hysteresis controllers, may also be

used.

In the second scheme, the motor currents are ﬁrst trans-

formed into the rotor dq-reference frame using continuous

rotor position feedback and the measured rotor d- and q-

axes currents are then regulated in the rotor reference frame,

as indicated in Fig. 33.52. The main advantage of regulating

33 Motor Drives 889

Current Controllers

Current Reference Generator

and g adjustment

sin(Pq

+g)

sin(Pq

+g - 4p/3)

Spillover

Field

Weakening

ref

−

Speed Controller

Speed

Calculator

cref

bref

aref

Encoder

Motor

−

FIGURE 33.51 Speed-controlled drive with the inner torque loop via current control in the stator reference frame.

∗

q-axis

current

controller

d-axis

current

controller

inverse

d-q

transformation

d-q

transformation

INVERTER

−

FIGURE 33.52 Block diagram of a current-controlled drive.

the stator currents in the rotor reference frame, compared to

the stator reference frame as in the ﬁrst scheme, is that cur-

rent references now vary more slowly and hence suffer from

lower tracking error. At constant speed, the stator current ref-

erences are in fact dc quantities as opposed to ac quantities,

and hence the inevitable tracking errors of the former scheme

are easily removed by an integral-type controller. The other

advantage is that the current references may now include feed-

forward decoupling so as to remove the cross-coupling of the

d- and q-axes variables as shown in the motor representation

of Fig. 33.52. The latter scheme is currently preferred, since it

allows more direct control of the currents in the rotor reference

frame.

It should be noted that continuous transformations to and

from rotor dq-axes are required; hence the rotor-position sen-

sor is a mandatory requirement. Rotor-position sensors of

10–12 bit accuracy are normally required. This is generally

viewed as a weakness for this type of drive.

The general torque relationship of a sinewave motor sup-

plied from a current-source SPWM inverter is given by

890 M. F. Rahman et al.

Eq. (33.69) which is rewritten here.

T =



+(L

−L



(33.74)

Precise control of the developed-torque control requires

that both i

and i

be actively controlled in order to regulate

it to the level determined by the error of the speed controller.

For the surface-magnet synchronous motor, the large effective

airgap means that L

≈ L

, so that i

should be maintained

at zero level. This implies that the i

current reference in

Fig. 33.52 should be kept zero. For the interior-magnet motor,

> L

, so that i

and i

have to be controlled simultaneously

to develop the desired torque. A few modes of operation are

possible.

33.5.3.2 Operating Modes

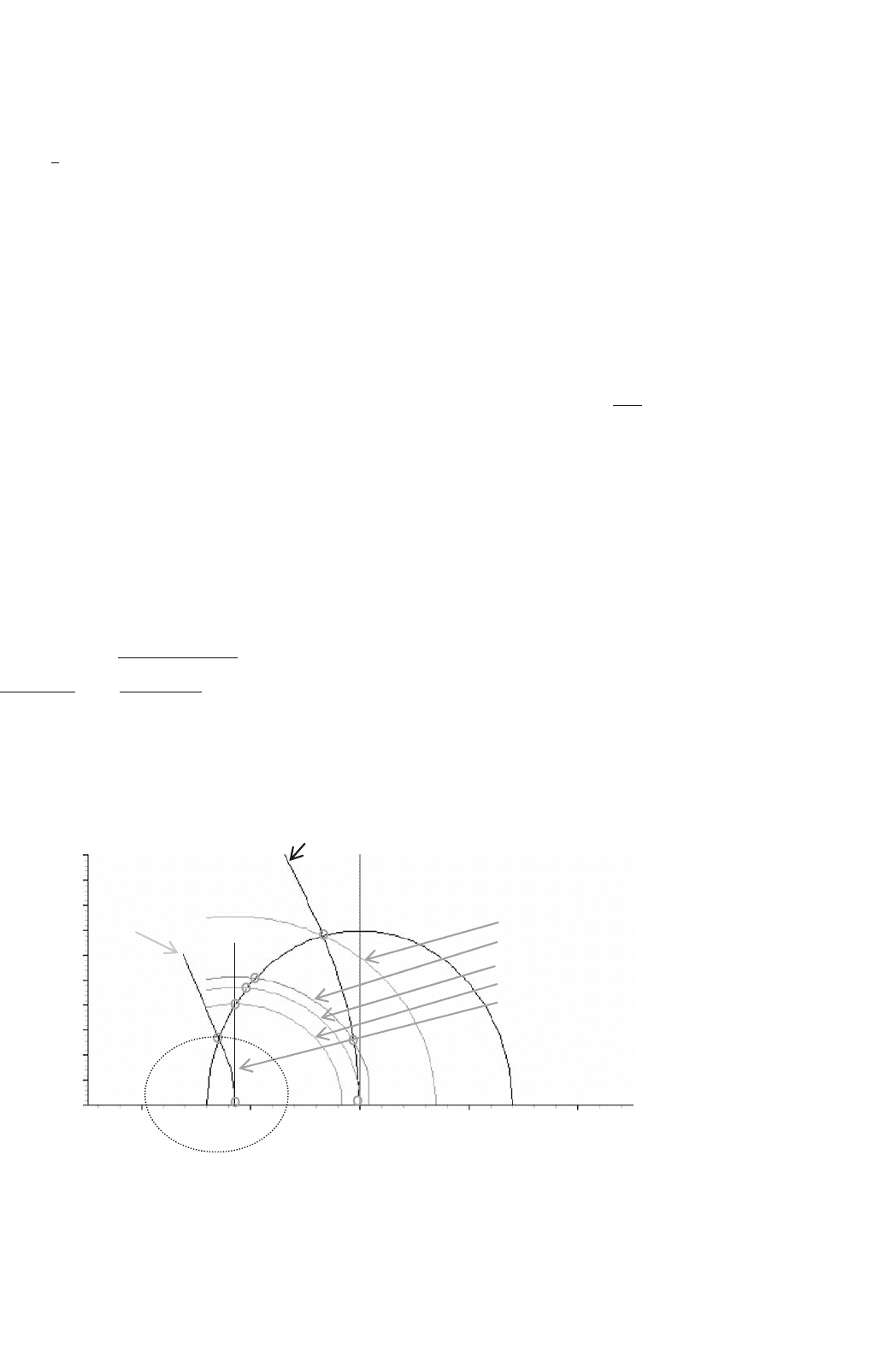
33.5.3.2.1 Operation with Maximum Torque per Ampere

(MTPA) Characteristic In this mode of control, the devel-

oped torque T per ampere of stator current is the highest for

a given rotor excitation. The combination of i

and i

that

develops the maximum torque per ampere of stator current

is indicated in Fig. 33.53. The reference signal for the inner

torque loop normally determines the i

reference; while the i

reference is given by

2(L

−L

)

−







4(L

−L

)

(33.75)

It should be noted that with i

= 0, this mode of operation

is achieved for the surface-magnet motor.

, A

Voltage limit

trajectory

Maximum torque per

ampere trajectory

Voltage limited

maximum output

trajectory

1.8

1.6

1.4

1.2

0.8

0.6

0.4

0.2

−2 −10 1 2

w = w

w = 1500 rpm = w

base

w = 2400 rpm = w

w = 2800 rpm = w

w > 2800 rpm

w = 2200 rpm

FIGURE 33.53 i

–i

Trajectories for the maximum torque per ampere characteristic and for maximum voltage and current limits of an interior

PM motor.

33.5.3.2.2 Operation with Voltage and Current Limits The

maximum current limit of the motor/inverter, I

smax

, is nor-

mally imposed by setting appropriate limits on i

and i

such

that

 I

s max

(33.76)

Equation (33.75) deﬁnes a circle around the origin of the

–i

plane.

The available dc-link voltage to the inverter places an upper

limit of the motor phase voltage, V

smax

, given by

= V

≤ V

max

(33.77)

)

+(L

+λ

)

≤





(33.78)

where the stator voltages v

and v

are expressed in the rotor

reference frame, as in Eq. (33.68). Equation (33.78) is obtained

from the voltage equation of Eq. (33.68) when the phase

resistance R is neglected. Equation (33.78) deﬁnes elliptical tra-

jectories that contract as speed increases. All the three modes

of operation are included in Fig. 33.53.

33.5.3.2.3 Operation with Field Weakening This mode of

operation is normally required for operating the motor above

the base speed. A constant-power characteristic is normally

desired over the full ﬁeld-weakening range. For a given rotor

excitation of λ

and developed power of P

, the developed

torque T and the net rotor ﬂux linkage required for constant-

power operation can be determined. From this, the limiting

values for i

and i

, which further constrain the allowable i

–i

trajectory is also indicated in Fig. 33.53, can be determined.

33 Motor Drives 891

Trajectory

Generator

∗

FIGURE 33.54 i

and i

trajectory generation satisfying the desired

operating modes.

The operating modes described in the preceding section are

normally included in a trajectory controller that generates the

references for i

and i

continuously, as indicated in Fig. 33.54.

33.6 Permanent-magnet Brushless DC

Motor Drives

33.6.1 Machine Background

Anyone studying electric machines would be aware that the

classical synchronous machine offers the possibility of the very

highest efﬁciencies. These machines have the power-carrying

conductors in the stationary part, therefore there is no need to

transfer high power through a brush system. The ﬁeld is pro-

vided on the rotating part either by an electromagnet, which

does require some very low-power brushes or at best, by a

permanent magnet with no power requirements at all.

This is clearly better than the traditional dc machine with

high-power brushes and rotating conductors, with those con-

ductors having a very poor path for heat to get away under

overload conditions. You might ask, “why did we use so many

of them?” It was of course because the dc machine offered the

ability to control the speed fully and easily, which the syn-

chronous machine, when running from the mains at a ﬁxed

frequency, was deﬁnitely not capable of. Thus, for example, all

electric trains and trams built up to the 1980s, many of them

still in service, use brushed dc motors.

The induction machine, the work horse of industry is quite

efﬁcient, but because of the need to carry magnetizing current

in the stator as well as load current, and the existence of slip, it

cannot be as good as the synchronous machine. It also innately

has a very limited speed range.

All this changed with the advent of inexpensive, reliable

power electronics. Quite suddenly power electronics engineers

had the ability to vary both the frequency and the amplitude

of an ac supply and thus to provide the holy grail of variable-

speed ac motors. This was ﬁrst applied to induction machines,

with the simplest form of open-loop control. The complexity

of control for synchronous machines added substantially to the

cost and was not so appealing. Today the thought of putting a

digital signal processor (DSP) or a microcontroller in a small

motor controller is no longer as daunting as it was ten years

ago, so the distinction between the complexity of a controller

for induction machines and synchronous machines has almost

disappeared.

Whilst power electronics radically changed our attitudes to

electric machine design and operation, there was a second very

important development which arrived on the scene at almost

the same time; the appearance of very powerful rare earth

permanent-magnet materials.

The ﬁrst rare earth magnet material was Samarium Cobalt,

used in very special applications such as space and defence,

but it was then, and still is, very expensive. Neodymium–Iron–

Boron (Nd–Fe–B) came next with even higher energy product.

Energy product is a measure used to quantify the effectiveness

of magnets. Nd–Fe–B began expensively, but has continued to

drop in price at a spectacular rate and recently became cheaper

than ferrites in term of dollars per unit of energy product.

Thus all the machines discussed here are permanent–magnet

(PM) machines, in general using Nd–Fe–B magnets.

33.6.1.1 Clarifying Torque Versus Speed Control

As is well understood, given a ﬁxed magnetic ﬂux level, the

magnitude of the current in a motor determines the magnitude

of the torque out of the machine. In a general application

if a torque is set, the speed is determined by the load. This

is what happens when driving an automobile. The throttle

or accelerator varies the torque. The speed can be very slow

or very high for the same foot position, depending on the

road conditions and vehicle motion history, even if the vehicle

is in the same gear. This principle of torque control rather

than speed control is fundamental to the operation of electric

machines. When speed control is required in PMBDCMs, it

is usual to implement torque control, with an extra outside

control loop, like a cruise control in an automobile, to use the

torque control to deliver speed control. So from here on the

discussion will describe torque control for the variable-speed

motor.

33.6.1.2 Permanent-magnet AC Machines

There are two quite different types of permanent-magnet

ac machines, actually looking very similar in their physi-

cal realization but dramatically different in their electrical

characteristics and in the way in which they are controlled.

33.6.1.2.1 Permanent-magnet Synchronous Machines

These are simple extensions of the classical synchronous

machine, where all of the voltages and currents are designed

to be sinusoidal functions of time, as they are in the syn-

chronous machine when used as a supply generator. These

machines are known as permanent-magnet synchronous

machines (PMSMs) or brushless ac machines and are discussed

elsewhere in this book. Whilst the application of sinusoidal

waveforms everywhere is comforting to many and does result

892 M. F. Rahman et al.

in less acoustic noise, less “stray losses” etc. there is in gen-

eral a requirement to know the exact rotor angular position

at every instant of time, with an accuracy in the order of one

degree. This knowledge is then used to shape the current wave-

forms to be sure that they are in phase with the back-emf of

the windings. Whilst much research is going on to run these

machines without position sensors, the reality in the workplace

today is that you need to include a relatively expensive shaft

position encoder with your PMSM, if you wish to control it

electronically.

33.6.1.2.2 Permanent-magnet Brushless DC Machines A

very much simpler possibility has emerged, which also gives

the beneﬁts of smooth torque and rapid controllability. This

results in smaller minimum machine size, yielding maximum

machine power density.

For this variant, the current waveforms and the back-

emf waveforms are trapezoidal rather than sinusoidal. In this

case, the machine is known as a permanent-magnet brush-

less dc machine (PMBDCM), with waveforms as shown in

Fig. 33.55.

33.6.1.3 Brief Tutorial on Electric Machine Operation

The operation of electric machines can be explained in a variety

of ways. Two possible and different methods are by:

(1) Using an understanding of the interaction of magnetic

ﬁelds and the tendency of magnetic ﬁelds to align.

This tendency to align is what provides the force that

time

angleBr

360°180°

FIGURE 33.55 Phase currents as functions of time and the ﬂux density

on the surface of the rotor as a function of angular position for a typical

PMBDCM.

makes a compass needle swing around, until it aligns

with the earth’s magnetic ﬁeld.

(2) Using the physical principle that “a current carrying

conductor in a magnetic ﬁeld has a force exerted on

it.” This force is commonly known as the Lorentz

force.

The difference between the two explanations is that the ﬁrst

method gives better “physical pictures.” However when one

gets a little more serious, wanting to put in numbers, the force

equations, whilst not greatly more difﬁcult, are a little more

challenging as they involve vector cross products.

With the second method, once the principle is accepted,

there is a particularly simple scalar version of the force equa-

tion that very rapidly and simply gives numeric answers.

The directions of the force, current, and motion are all

orthogonal, i.e. at right angles and a formal exposition would

again use a vector cross product. However, provided the rules

learned in high school science are applied, the scalar version,

F = BLI can be used, where F is the force in newtons, B is

the ﬂux density in Tesla, L is the length of the conductor in

meters, and I is the current in amperes.

Let us try both the methods, on the simple machine of

Fig. 33.56.

The rotor is a magnet with a north and a south pole, and

there is a coil of wire in the slots in the stator. Current is

shown going into the conductor called a at the top of the sta-

tor and coming out of the conductor called a



at the bottom.

To simulate a real machine more closely, one should imagine

putting a one turn “coil” of wire into the slot, with a connec-

tion made at the back of the machine to connect the top wire

to the bottom, so that by applying a positive voltage to the top

wire and a negative voltage to the end of the coil (the bottom

wire), current will ﬂow in at the top and out at the bottom as

discussed previously.

FIGURE 33.56 A simple motor with a single coil in the stator and a

permanent-magnet rotor.

33 Motor Drives 893

Method 1 If the current is put into the top and comes out

of the bottom as marked, then according to the right-hand

rule (if you forget, then look at the Institution of Electrical

and Electronic Engineers (IEEE) logo), magnetic ﬂux will be

forced to go through the center of the coil from right to the

left, creating a north pole on the left. The ﬂux will then double

back through the iron frame of the motor to arrive back at the

South pole on the right.

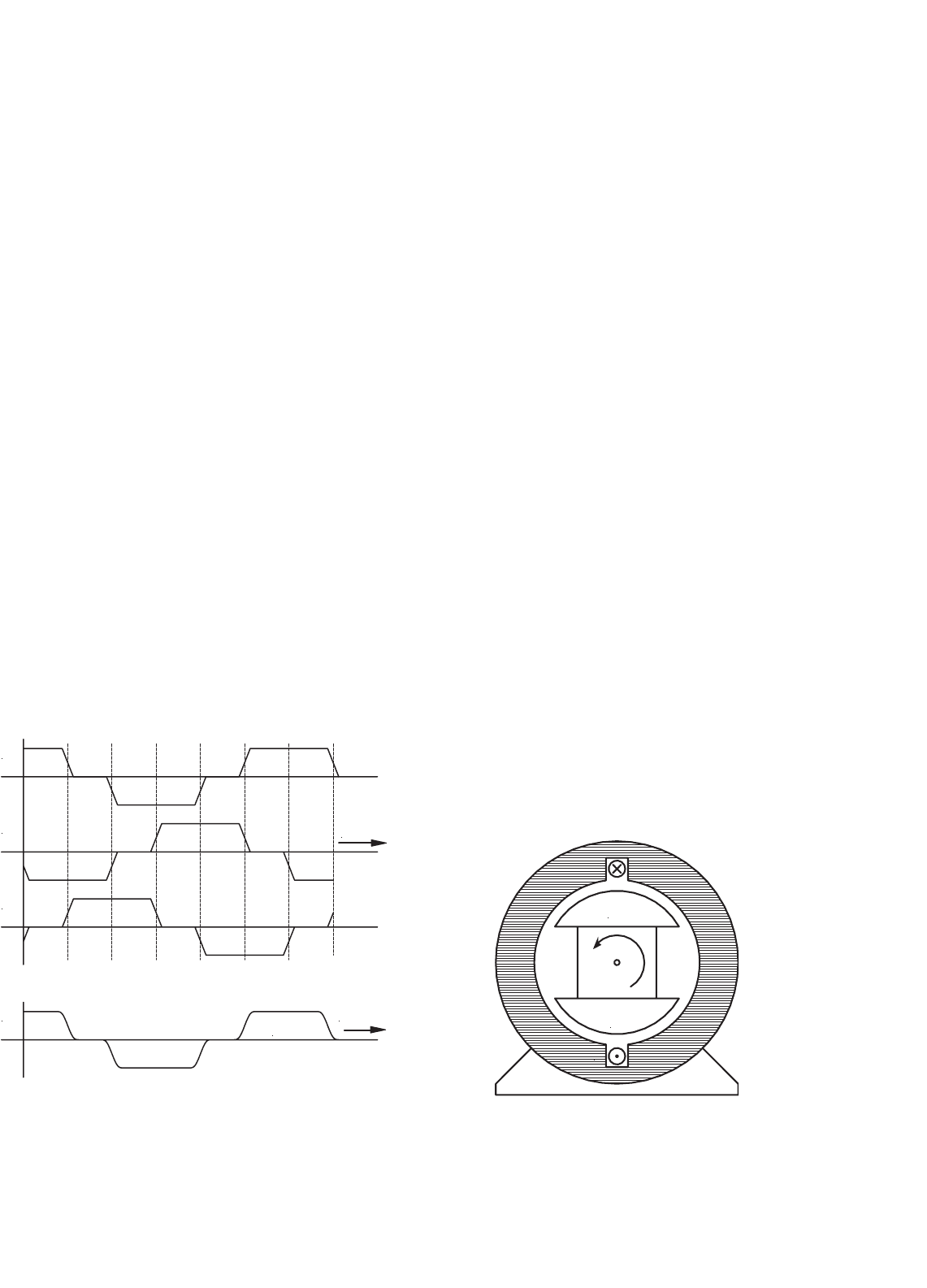
Figure 33.57 shows a computer generated magnetic ﬁeld

plot. This was produced using ﬁnite element analysis and mod-

eling the stator as electrical steel, the volume in the center as

air and injecting current into the coil.

If the permanent-magnet rotor is then put inside the

stator of Fig. 33.57, the rotor will align by rotating 90

◦

counterclockwise.

FIGURE 33.57 A computer generated magnetic ﬁeld for current in the

windings and a stator made of electrical steel.

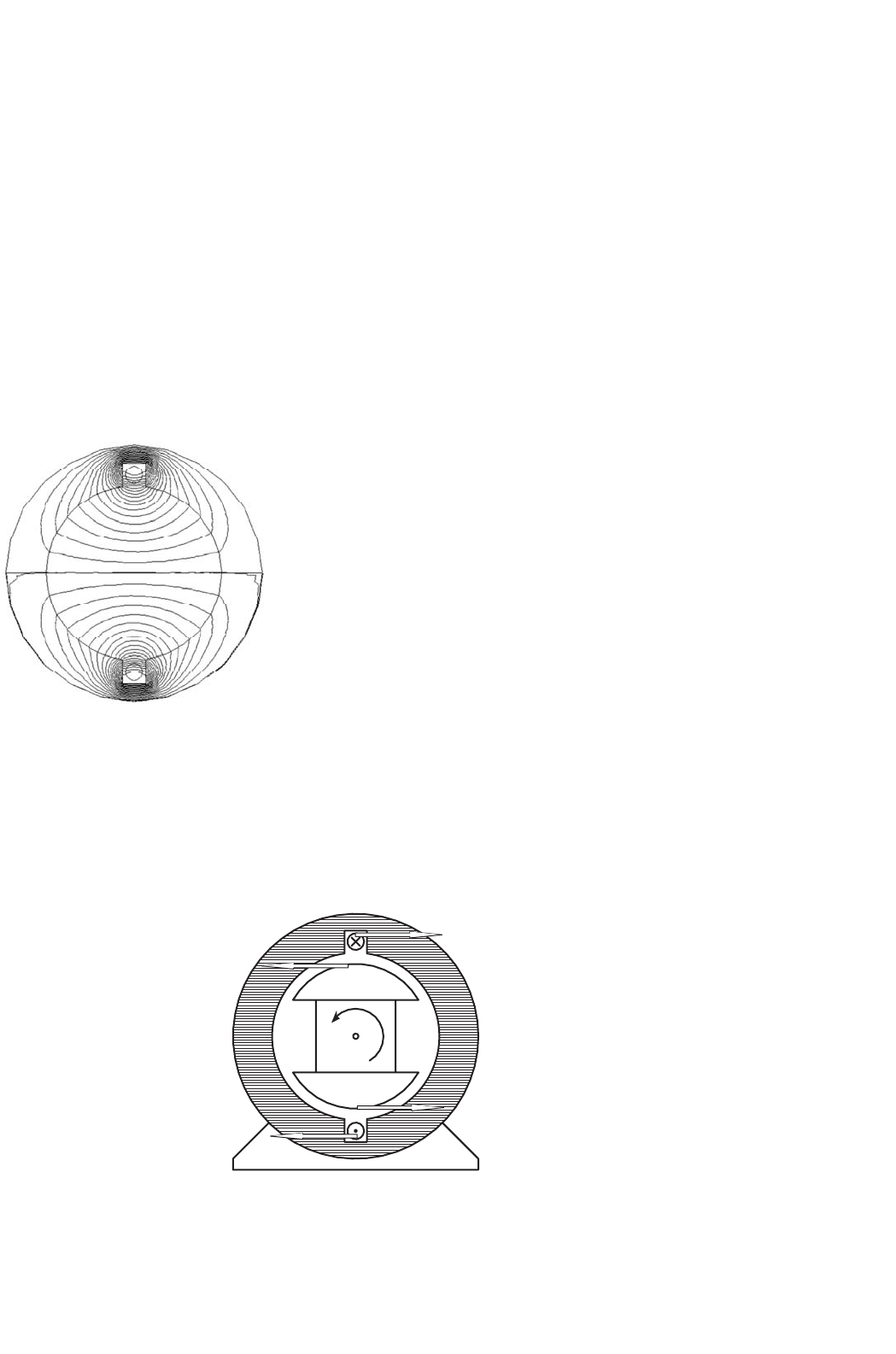
Method 2 In this case, looking at Fig. 33.58, the conductor

a will be immersed in a quite dense ﬁeld produced by the

magnets, with the ﬂux lines going up the page in the rotor,

Force on conductor a

Reaction force on magnet N

Force on conductor a′

Reaction force on magnet S

FIGURE 33.58 Lorentz forces on conductor and rotor of a simple machine.

across the airgap into the steel of the stator, heading down the

stator to jump back across the lower airgap to return to the

south pole. If a current is directed into the upper conductor

and out of the bottom as before, it will produce force. Applying

the direction rules associated with the Lorentz force, the force

on the conductor will be to the right at the top and to the left

at the bottom. Invoking Newton’s third law, that action and

reaction are equal and opposite, it is clear that if the wire is

ﬁxed, as it is, then there will be a force on the rotor to the left

at the top and to the right at the bottom, thus the rotor will

move counterclockwise as before.

33.6.2 Electronic Commutation

If the rotor of Fig. 33.58 moves, then to keep it rotating in the

same direction, sooner or later the current in the conductors

must be reversed. The time at which that needs to be done is

when the rotor has moved to an almost aligned position, so it is

not really a matter of time, but a matter of rotor position. Since

the rotor is a permanent magnet, it is a very simple matter

to determine at least where the physical pole edges are, using

simple, reliable and inexpensive Hall effect (HE) sensors. These

are small semiconductor devices which respond to magnetic

ﬂux density. (There are many ways to sense the position of the

rotor; however the remainder of this exposition will stay with

the HE sensor for simplicity.)

A very simple motor, relying on the inertia of the rotor for

continuous rotation, could have a control circuit which sensed

when the rotor magnet was horizontal and then reversed the

current in aa



of Fig. 33.58.

The traditional “H” bridge switching circuit shown in

Fig. 33.59 does that very effectively. Switch drive logic must

ensure that either S1 and S4 are on, or S2 and S3 are on and

never S1 and S2 simultaneously, or S3 and S4 simultaneously.

This simultaneous operation would provide a short circuit.

When this happens due to errors in the switch drive signal it

is called “shoot through.” There are generally important parts

894 M. F. Rahman et al.

a′

−

FIGURE 33.59 An “H” bridge circuit that can reverse the current

through aa



, as drawn with mechanical switches.

of the switch drive signal logic, discussed later, which try to

make this impossible in normal operation.

In real motors, the permanent-magnet rotor ﬁeld does

not change instantaneously from north to south as the rotor

rotates, so there would be reasonably large angles over which

the torque could not be effectively produced. Also more coils

are put in so that the space of the machine frame is used more

efﬁciently.

The use of three “phases,” as in Fig. 33.60, is very common.

There are many things which balance naturally in a three-phase

system and it is the simplest system with which it is possible

to develop constant and unidirectional torque at all times and

positions.

A very common method has developed, known as “six step

switching.” In this system, three phases are used. They are

connected in star and there is a space between each of the

a′

b′

c′

FIGURE 33.60 The physical layout of a three-phase PMBDCM.

magnet poles on the rotor and the two phases are activated

at any one time, the third “resting” as the space between the

magnet poles passes over it.

While the motor in Fig. 33.60 looks just like a three-phase

synchronous machine, its operation is rather different.

As stated above, the windings are invariably star connected,

as shown in Fig. 33.61.

b′

a′

c′

FIGURE 33.61 The schematic connection of the windings shown in

Fig. 33.60.

Six Step Switching Explained

Consider the coil aa



, as shown in Fig. 33.60 and also diagram-

matically in Fig. 33.61. Current driven into the a terminal,

coming out of the a



terminal, will produce, as discussed

before, ﬂux from left to right, as shown here.

Obviously if the current direction in aa



is reversed, the ﬂux

will be

Similarly if current is driven into b and out of b



ﬂux will result

And if it is reversed,

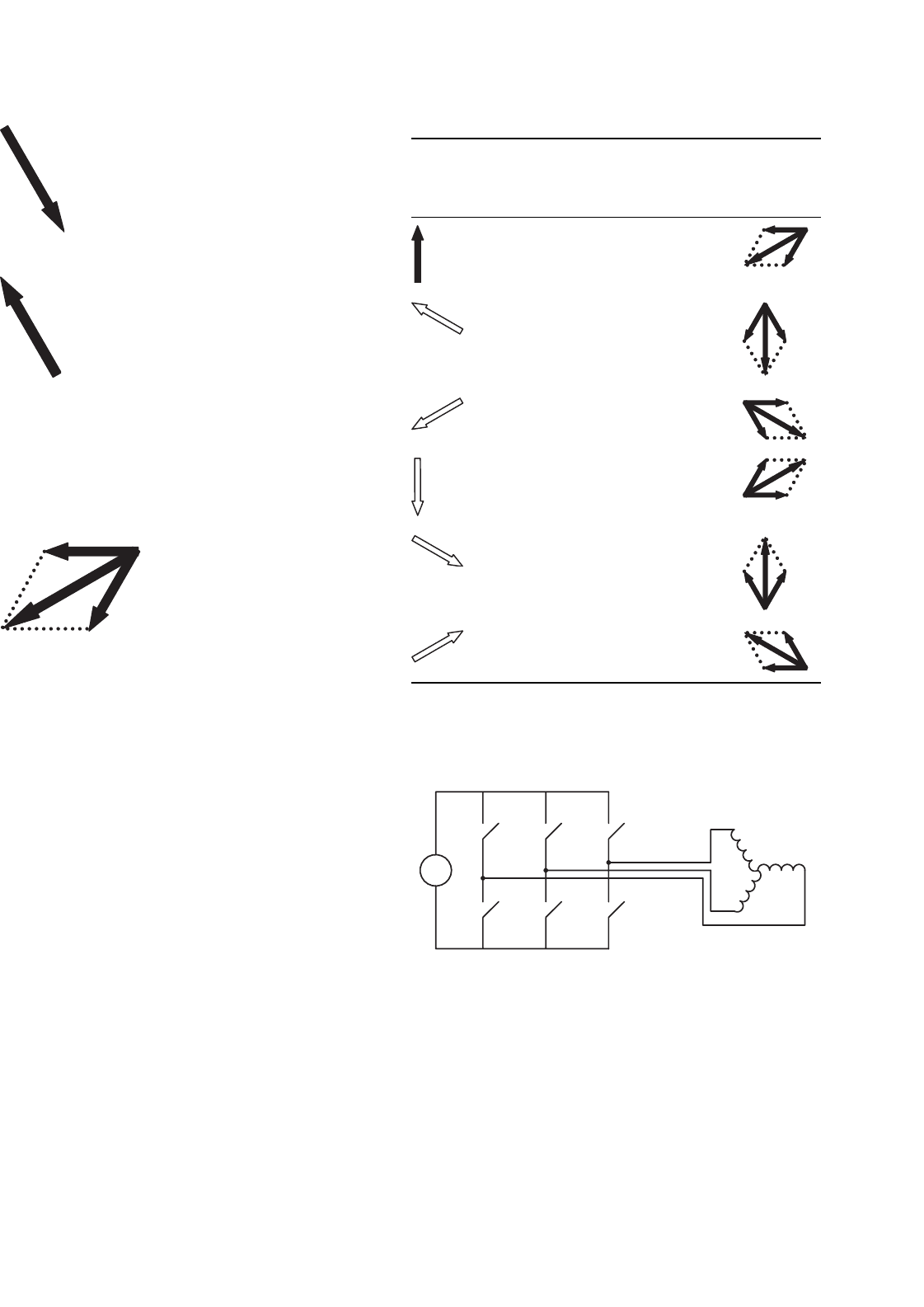
33 Motor Drives 895

Finally, if current is driven into c and out of c



, ﬂux will result

And if it is reversed,

The permanent-magnet rotor would tend to align with the

ﬂux arrow shown in each of the states above, as discussed

under machine operation, Method 1.

Now if the motor is wired in star as shown in Fig. 33.61,

and a steady current is driven into a and out of b, the ﬁrst and

the fourth cases above occur at the same time. They add to

produce a resultant,

and the rotor will tend to align with this resultant.

The Hall effect sensors are positioned so that just as the rotor

gets to within 60

◦

of being aligned, another arrangement of the

windings is energized, and the ﬁeld jumps forward another

◦

, so the rotor is 120

◦

away from being aligned. The rotor is

always an average of 90

◦

away from its desired position!

If a controller has input power from positive and negative of

a dc supply and outputs to the terminals a, b, and c only, then

the sequence of connections shown in Table 33.2 will produce

the resultant ﬂux directions as shown, providing continuous

rotation.

The switching of Table 33.2 is simply achieved by a vari-

ant of the “H” bridge, as shown in Fig. 33.62. This process of

switching current into different windings is called commuta-

tion and is the equivalent of the sliding brush contacts in a

traditional brushed dc machine.

33.6.3 Current/Torque Control

You may have noted that the discussion has been about current

in the windings rather than the voltage across them. In very

simple small brushless DC machines, like the one in the mufﬁn

fan in your computer power supply, voltages are connected

directly to the windings. For these small motors, the resistance

of the windings is relatively high and this helps limit the actual

current that ﬂows and swamps inductive effects.

TABLE 33.2 The sequence of connections which results in counterclock-

wise continuous rotation of the rotor of the PMBDCM of Fig. 33.60

When rotor gets

to this position,

connections are

made as at right

Terminal a Terminal b Terminal c Flux directions

Current in Current out Zero

Zero Current out Current in

Current out Zero Current in

Current out Current in Zero

Zero Current in Current out

Current in Zero Current out

a′

−

b′

c′

FIGURE 33.62 The switching circuit used for commutation of a

PMBDCM.

There is an extra difﬁculty that must be addressed with high-

performance, high-efﬁciency, well-made machines, and it adds

another layer to the control of the motor. Such machines can

easily be designed with very low resistance windings. It is not

uncommon to have windings for a 200 V machine at the 20 kw

level with the winding resistances less than 0.1 .