Понетаева Н.Х., Патрушева Н.В. Начертательная геометрия в примерах и задачах
Подождите немного. Документ загружается.


68
Угол
ϕ
между вырожденной проекцией В*
2
А
2
С*
2
и осью ОХ определяет натуральную величину угла
наклона плоскости треугольника ABC к горизонтальной плоскости проекций.
Чтобы произвольно расположенную плоскость перевести в горизонтально проецирующее положение, за
ось вращения нужно выбирать фронтально проецирующую прямую. Плоскость вращением переводится в
положение, когда ее фронталь перпендикулярна горизонтальной плоскости проекций П
1
.
Пример 4.8
Определить угол
ψ
наклона плоскости
α
, заданной следами, к фронтальной плоскости проекций П
2
.
Рис. 4.21
Для определения угла
ψ
=
α
^П
2
плоскость
α
повернем вокруг фронтально проецирующей оси I ⊥
П
2
в положение горизонтально проецирующей плоскости
α
*.
Сначала выполнено вращение фронтального следа
α
П2
в положение
α
*
П2
⊥OХ при помощи
перпендикуляра I
2
К
2
, опущенного из I
2
на
α
П2
. Кроме следа
α
П2
вращаем вокруг оси фронталь AM плоскости
α
,
пересекающую ось I. Когда фронтальный след
α
П2
занял положение, перпендикулярное оси ОХ,
горизонтальная проекция A
1
M
1
фронтали AM вырождается в точку А
1
=М
1
. Соединив эту точку с новой точкой схода
следов
α
*
х
, получим новый горизонтальный след
α
*
П1
.
Угол
ψ
между новым горизонтальным следом и осью координат ОХ определяет натуральную величину
угла наклона плоскости
α
к фронтальной плоскости проекций П
2
.
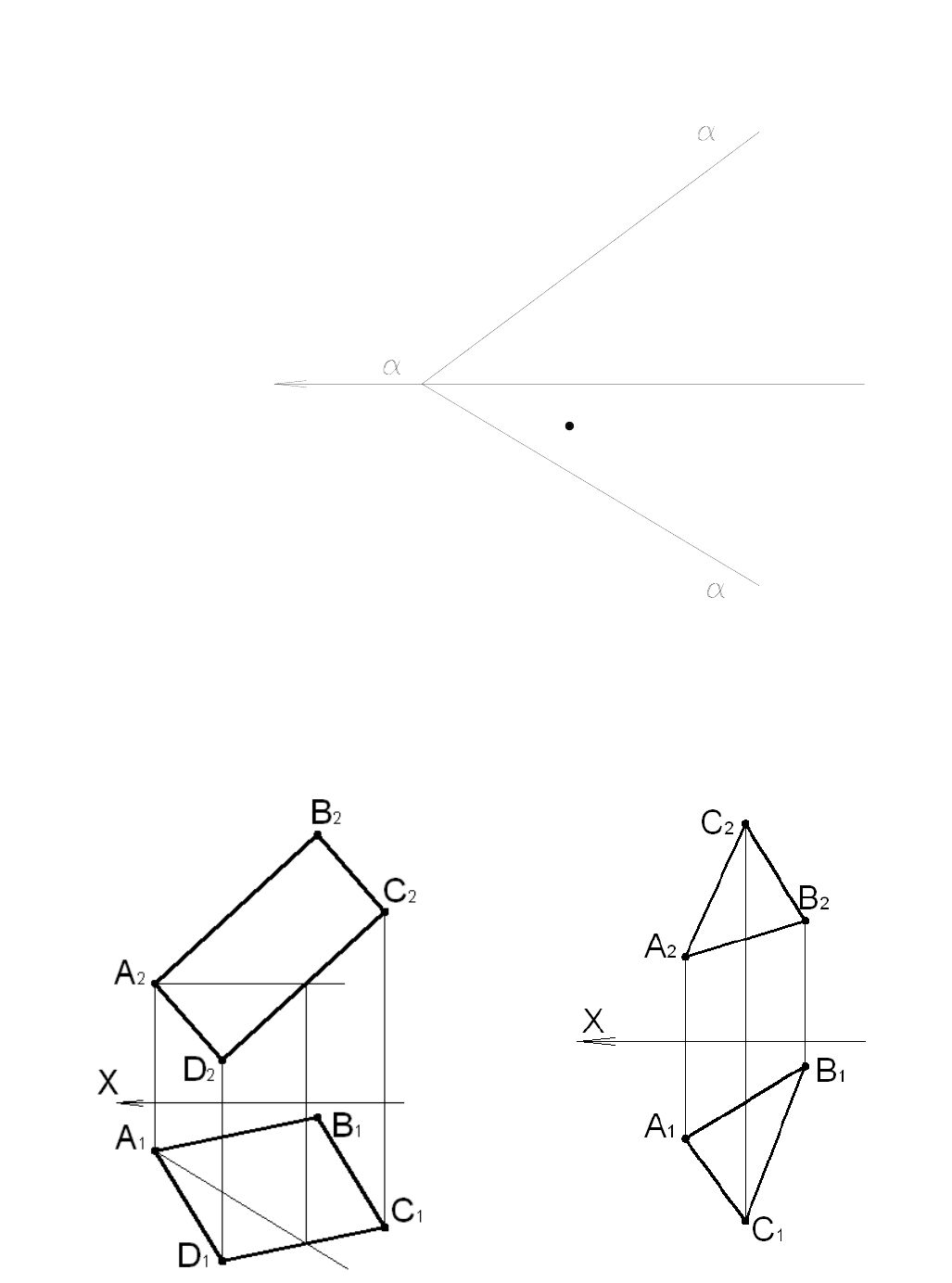
Задача 4.9
Определить натуральную величину отрезка AB и углы его наклона к плоскостям проекций П
1
и П
2
Рис. 4.22
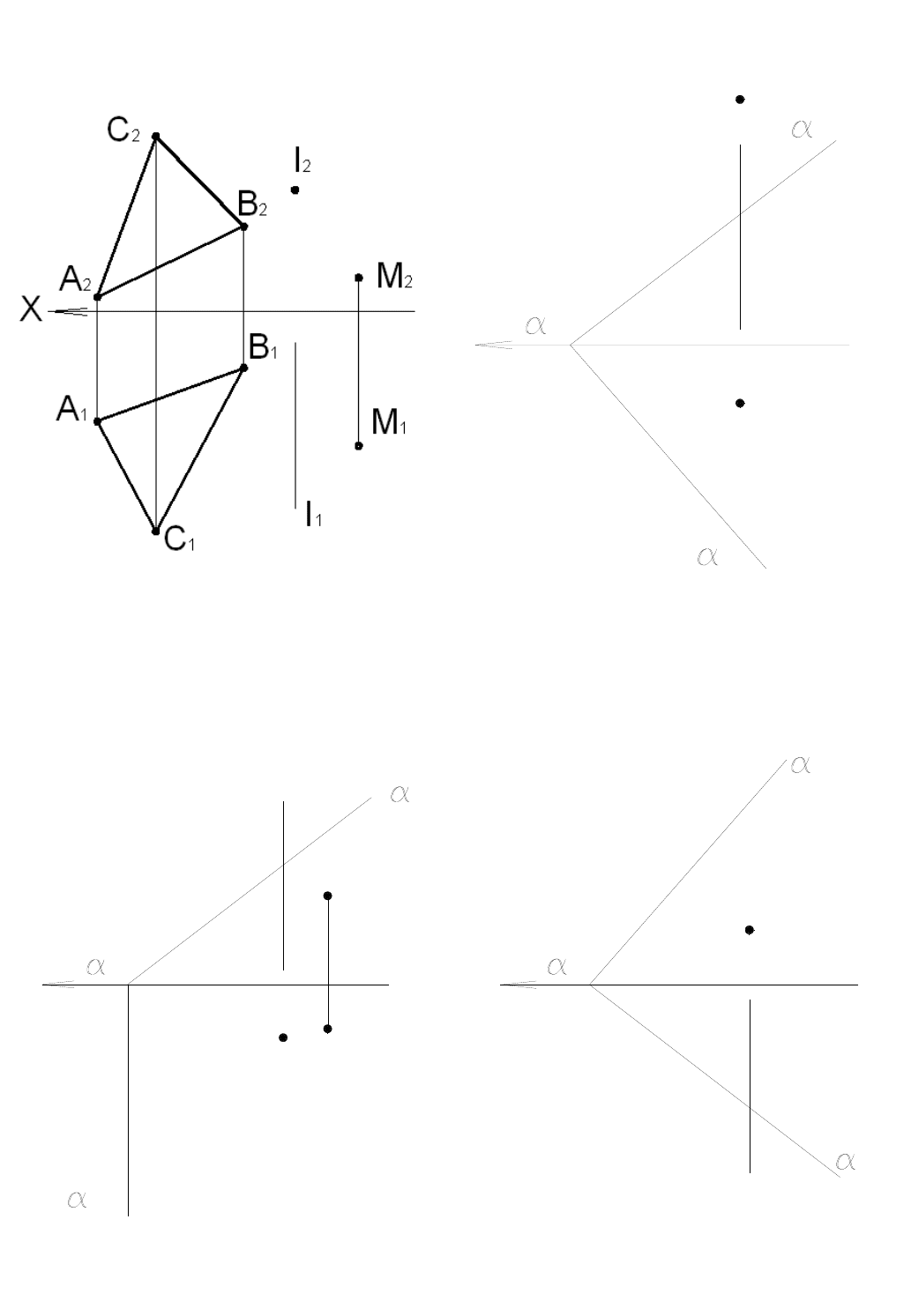
69
Задача 4.10
Построить проекции точки M, повернутой вокруг
оси I до совмещения с плоскостью
ΔABC.
Задача 4.11
Определить расстояние от точки A до плоскости
α
вращением вокруг оси I.
Рис. 4.23 Рис. 4.24
Задача 4.12
Повернуть плоскость
α
вокруг оси I до
совмещения с точкой A. Новое положение
плоскости задать тремя точками.
Задача 4.13
Определить угол наклона плоскости
α
к П
2
.
Рис. 4.25 Рис. 4.26
X
П1
П2
X
A2
I1=A1
I2
X
П1
П2
X
A1
I2
A2
I1
X
П1
П2
X
I2
I1
70
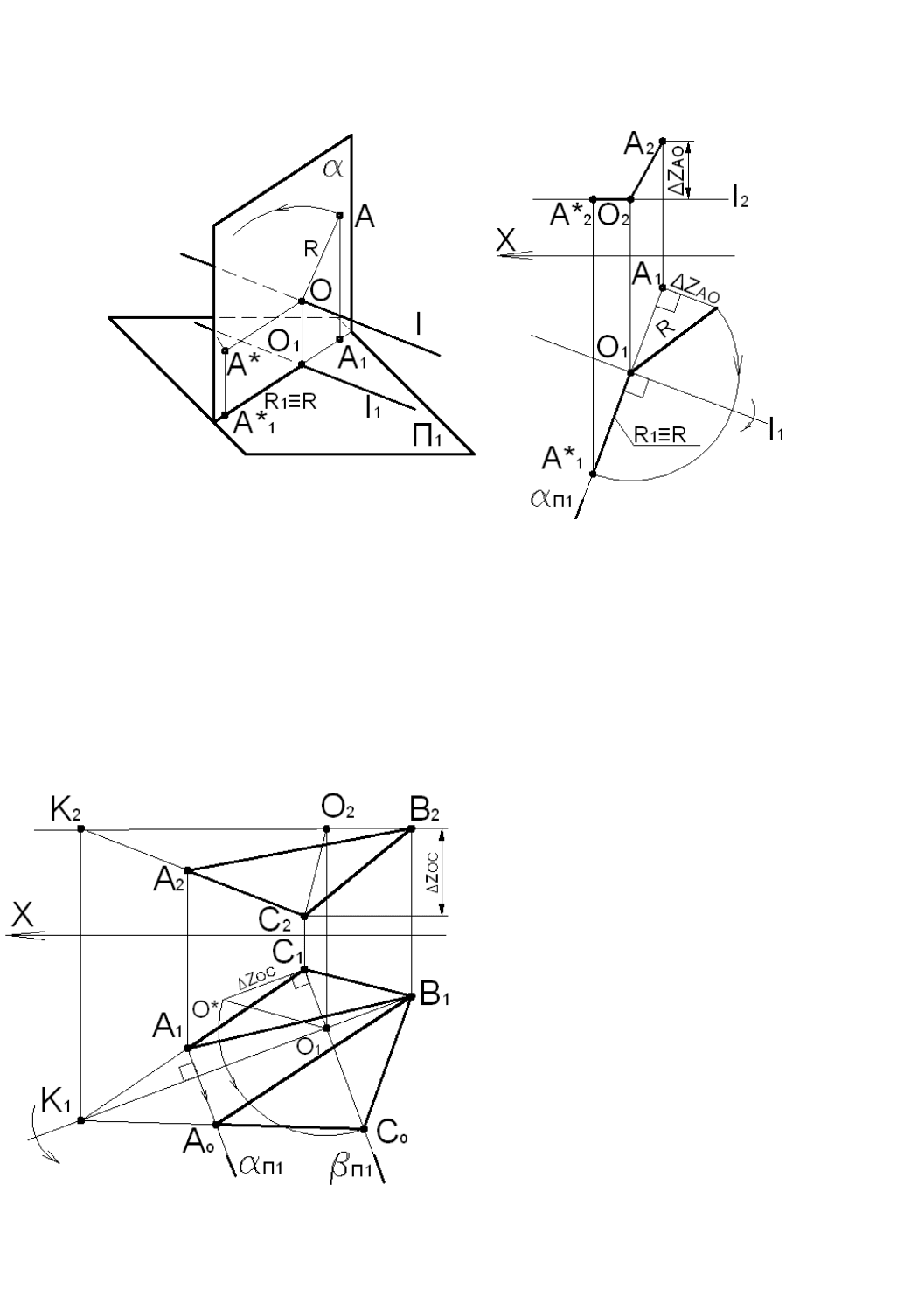
4.4. Вращение вокруг прямых уровня. Совмещение
Пример 4.9
Повернуть точку А вокруг оси, параллельной горизонтальной плоскости проекций (горизонтали) так,
чтобы радиус вращения занял положение, параллельное горизонтальной плоскости проекций П
1
.
Рис. 4.27
Точка А вращается в горизонтально проецирующей плоскости
α
, перпендикулярной оси вращения I:
А∈
α
,
α
⊥ I ∧ I|| П
1
,
α
⊥П
1
. Горизонтальный след
α
П1
плоскости
α
проходит через A
1
и перпендикулярен
оси вращения: А
1
∈
α
П1
,
α
П1
⊥ I
1
. Центр вращения О является точкой пересечения оси вращения с плоскостью α:
O=l ∩
α
. Радиус вращения точки A: AO ⊥I, |AO| = IRI.
Если повернуть АО до положения, параллельного плоскости П
1
то проекция R, на плоскость П
1
будет
равна натуральной величине |АО|. На основании теоремы о проекциях прямого угла горизонтальная проекция
точки A может перемещаться только по перпендикуляру к горизонтальной проекции горизонтали. A*
1
O
1
=IAOI=R.
Натуральная величина радиуса вращения R равна гипотенузе вспомогательного прямоугольного
треугольника, один катет которого равен горизонтальной проекции А
1
О
1
радиуса АО, а другой – разности
удалений точек А и О от плоскости П
1
- DZ
A0
.
А*
1
и А*
2
- новые горизонтальная и фронтальная проекции повернутой точки А.
Пример 4.10
Найти натуральную величину
треугольника ABC способом вращения
вокруг горизонтали. Горизонталь провести
вне треугольника ABC.
В плоскости треугольника через вершину
В проводим горизонталь ВК. Фронтальная
проекция горизонтали В
2
К
2
параллельна оси ОХ.
Точка К одновременно принадлежит стороне АС:
ВК‖П
1
.
ВК ∈ DАВС, B
2
K
2
‖OX, К
2
∈ А
2
С
2
, K
1
∈ A
1
C
1
.
Точки А и С вращаются в горизонтально
проецирующих плоскостях
α
и
β
,
перпендикулярных оси вращения ВК:
α
⊥BK,
β
⊥BK,
α
П1
⊥ B
1
K
1
,
β
П1
⊥В
1
К
1
.
Точка В не меняет своего положения.
Когда треугольник займет положение,
параллельное горизонтальной плоскости проекций,
радиусы вращения точек А и С станут
параллельны П
1
.и спроецируются на плоскость
проекций в натуральную величину.
Рис. 4.28
71
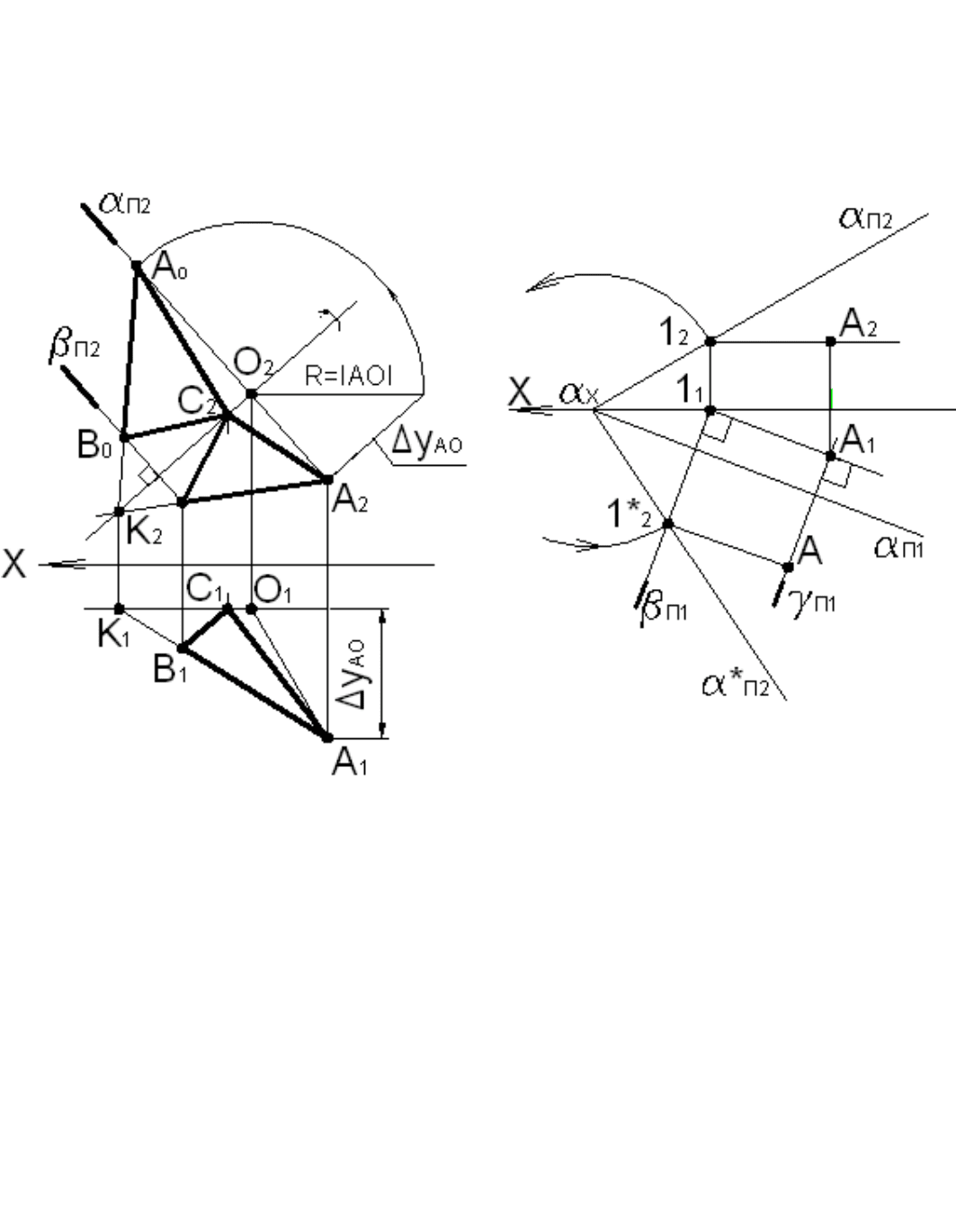
Центром вращения точки C является точка O = ВК ∩
α
, радиусом вращения – отрезок |OC| = R.
Натуральную величину IOCI определяем, используя способ прямоугольного треугольника.
От центра вращения О точки С по направлению следа
α
П1
откладываем длину радиуса вращения и
отмечаем новую горизонтальную проекцию С
о
точки С . Новую проекцию A
о
точки A определяем из условия, что
точка А принадлежит прямой СК и плоскости
β
, в которой она вращается: А
O
∈К
1
C
O
∧ А
о
∈
β
П1
Рис. 4.29 Рис. 4.30
А
0
В
1
С - натуральная величина треугольника ABC.
На рис. 4.29 приведен пример определения натуральной величины треугольника ABC, решенный
способом вращения вокруг фронтали СК. Для определения натуральной величины треугольник
поворачивается вокруг оси, параллельной фронтальной плоскости проекций П
2
, до положения, параллельного
плоскости проекций П
2
.
Если за ось вращения принять нулевую линию уровня (след плоскости), то такое вращение будет
называться совмещением.
На рис. 4.30 плоскость общего положения
α
с принадлежащей ей точкой А совмещена с горизонтальной
плоскостью проекций П
]
вращением вокруг горизонтального следа
α
П1
.
Чтобы построить совмещенное положение A, принадлежащей плоскости
α
, достаточно построить
совмещенный след
α
*
П2
и провести совмещенную горизонталь, которой принадлежит точка А. Для
построения совмещенного следа
α
*
П2
определено совмещенное положение 1*
2
точки 1∈
α
П2
. Через точку 1
проведена горизонтально проецирующая плоскость
β
, в которой вращается точка 1. Расстояние отточки
схода следов
α
х
до точки 1
2
истинное, поэтому точка 1*
2
определена на пересечении дуги из центра
α
х
радиусом R =
α
x
1
2
и горизонтального следа
β
П1
плоскости
β
, 1 ∈
β
.
Искомая точка A определяется в пересечении совмещенной горизонтали А -1*
2
и горизонтального следа γ
П1
плоскости
γ
, в которой вращается точка А.
72
Пример 4.11
В плоскости
α
задана точка A. Построить прямоугольный треугольник ABC, сторона которого
АС составляет с горизонтальным следом плоскости угол 30º. Катет │AC│=35 мм, катет │AB│=20
мм.
Рис. 4.31
Совместим плоскость
α
общего положения с горизонтальной плоскостью проекций, то есть будем
вращать плоскость
α
вокруг горизонтального следа
α
П1
.
Проведем через точку А горизонталь плоскости. Выберем точку 1, лежащую на фронтальном следе, она
совпадает со своей фронтальной проекцией 1
2
(1
1
– горизонтальная проекция точки 1). Проведем прямую
1
1
2
1
перпендикулярно оси вращения – горизонтальному следу плоскости –
α
П1
. На этой прямой должна
находиться точка 1 (после совмещения плоскости
α
с плоскостью П
1
) на расстоянии, равном радиусу вращения
точки 1. Длину радиуса вращения можно определить как гипотенузу прямоугольного треугольника с катетами
2
1
1
1
и 1
1
1*.
Проведя из точки схода следов
α
х
дугу радиусом
α
х
1
2
до пересечения с прямой 1
1
2
1
, получаем новое
совмещенное с плоскостью П
1
положение точки 1 (точка 1*
2
). Через нее проводим совмещенный след
α
*
П2
.
Строим треугольник ABC в соответствии с условиями примера в натуральную величину. Чтобы
построить проекции треугольника, принадлежащего плоскости
α
, поступим следующим образом. Каждая
точка плоскости принадлежит горизонтали или фронтали плоскости, поэтому через точки A, В и C проводим,
например, горизонтали плоскости. Горизонталь плоскости, на которой расположена точка А, уже построена
(А1*
2
,1
1
A
1
, 1
2
А
2
). Горизонтали через точки B и C строим аналогично. По линиям проекционной связи находим
горизонтальные и фронтальные проекции вершин треугольника A, В и С.
73
Задача 4.14
В плоскости
α
построить равносторонний треугольник ABC, сторона которого АС принадлежит
горизонтали плоскости
α
. │АС│=30 мм. Использовать способ совмещения.
Рис. 4.32
Задача 4.15
Определить натуральную величину
параллелограмма ABCD. Использовать способ
вращения вокруг горизонтали.
Задача 4.16
Определить натуральную величину треугольника
ABC. Использовать способ вращения вокруг
фронтали.
Рис. 4.33 Рис. 4.34
X
П1
П2
X
A1

75
З
адача 4.17
П
ровести биссектрису угла B в треугольнике
A
BC. Использовать способ вращения вокруг
ф
ронтали.
Задача 4.18
Определить расстояние от точки A до прямой m.
Рис. 4.35 Рис. 4.36
Задача 4.19
В плоскости
α
построить квадрат ABCD, сторона которого AB составляет с фронтальным следом
плоскости угол 30
o
и равна 20 мм.
Использовать способ совмещения (вращения вокруг фронтального
следа).
Рис. 4.37
76
Задача 4.20
В плоскости
α
построить окружность радиусом R= 15 мм. Точка O – центр основания. Использовать
способ совмещения.
Рис. 4.38

77
Для самостоятельной работы
78
5. Поверхности
5.1. Поверхности вращения. Принадлежность точки поверхности
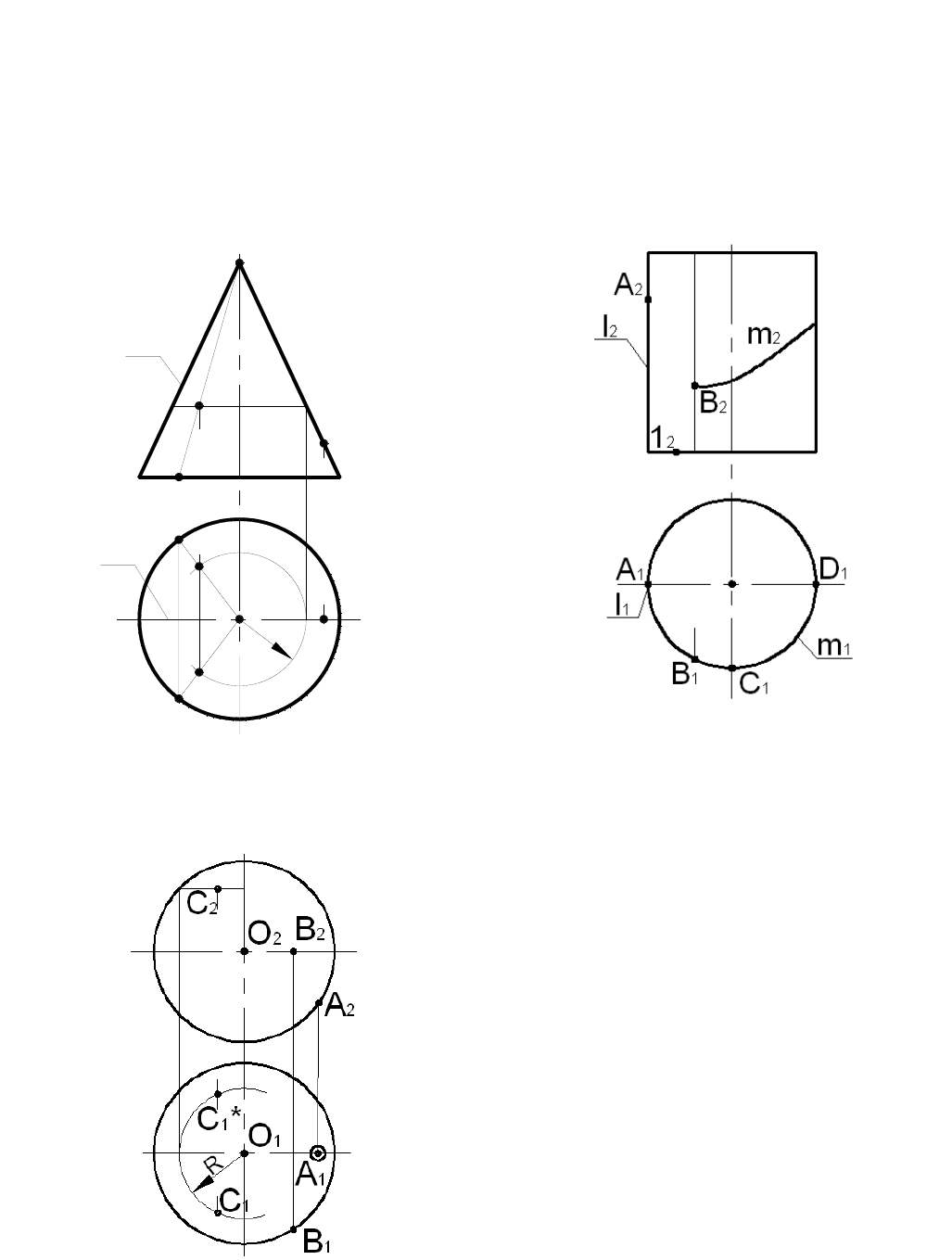
Поверхности вращения образованы вращением образующей вокруг неподвижной оси. Каждая точка
образующей описывает около оси окружность, и, следовательно, любая плоскость, перпендикулярная оси,
пересечет поверхность вращения по окружности – параллели. Параллель максимального радиуса
называется экватором. Плоскость, проходящая через ось поверхности вращения, пересекает поверхность по
меридиану. Главный меридиан получается при проведении через ось фронтальной плоскости уровня.
Точка, принадлежащая поверхности, расположена на некоторой линии, принадлежащей поверхности,
например, параллели или образующей.
Рис. 5.1 Рис. 5.2
Конус – образующая I пересекает ось вращения
в точке S. На рис по заданным проекциям А
1
и В
2
точек, принадлежащих конической поверхности,
надо было найти проекции А
2
и В
1
. Построение
выполнено при помощи крайней правой образующей
S – А и образующей S – 1, проведенной через точку
В. Можно построить недостающую проекцию точки В
и с помощью параллели радиуса R.
Цилиндр – образующая l параллельна оси
вращения. На рис.5.2 для построения проекций
точек кривой линии m, принадлежащей поверхности
цилиндра, использованы образующие цилиндра,
проходящие через точки кривой.
Сфера – центр O образующей окружности
находится на оси вращения. На рис. 5.3 по
фронтальной проекции найдены горизонтальные
проекции точек A, В, С, принадлежащих поверхности
сферы. Проекция точки А
1
построена по условию
принадлежности точки главному меридиану сферы.
Точка В принадлежит экватору сферы. Для
определения С
1
построена горизонтальная проекция
параллели, проходящей через точку С, – окружность
радиуса R.
Рис. 5.3
S2
S1
l2
R
R
B2
12
B1*
B
1
l1
A2
A1
11*
1
1
