Понетаева Н.Х., Патрушева Н.В. Начертательная геометрия в примерах и задачах

Подождите немного. Документ загружается.

120

8. Плоскость, касательная к поверхности

Плоскостью, касательной к кривой поверхности в точке поверхности, называется плоскость,

определяемая двумя пересекающимися касательными прямыми к этой поверхности в точке.

Рис. 8.1

В точке поверхности можно провести единственную касательную плоскость к этой поверхности.

Для построения касательной плоскости к поверхности в точке достаточно на поверхности провести

через эту точку две любые простейшие линии и к каждой из них провести касательные. Две касательные

определяют касательную плоскость.

Плоскость, касательная к поверхности вращения в заданной на ней точке, определяется двумя

прямыми, касательными к параллели и меридиану поверхности (рис. 8.1).

У линейчатых поверхностей (например, конуса и цилиндра) одной из множества линий,

проходящих через заданную точку, является прямолинейная образующая.

Рис. 8.2 Рис. 8.3

Поскольку касательная к образующей в точке сливается с самой образующей, то касательная

плоскость касается поверхности по прямой образующей.

Касательная плоскость может касаться кривой поверхности по кривой линии, например, по

верхней или нижней параллели открытого тора.

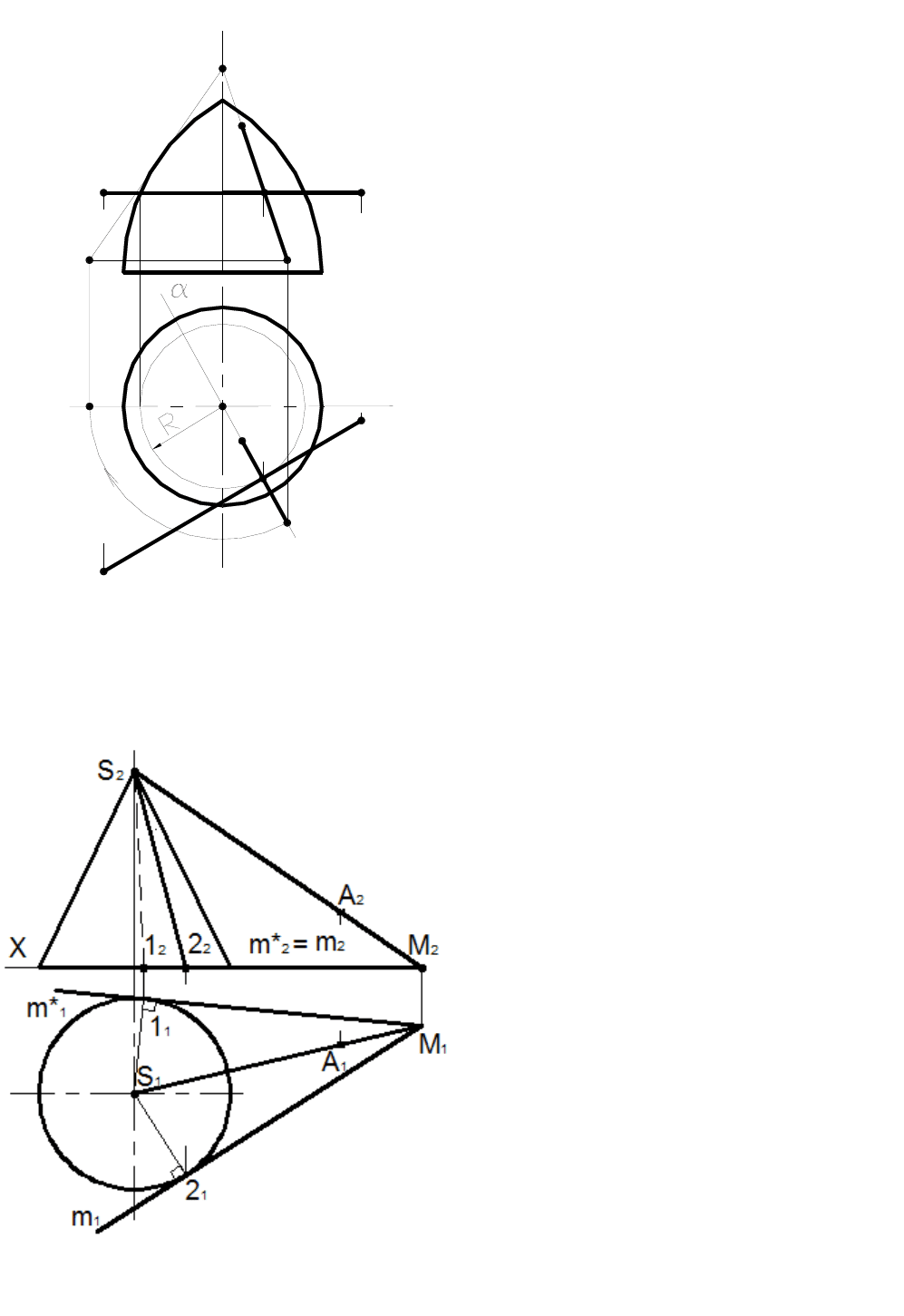
121

Пример 8.1

Построить касательную плоскость к

поверхности самопересекающегося тора в

заданной на поверхности точке K

(рис.8. 4).

Касательная плоскость определяется

касательной прямой АВ к параллели точки К и

касательной прямой CD к меридиану этой точки.

Меридиан точки К лежит в плоскости

проходящей через ось I поверхности и точку К.

Для определения фронтальной проекции C

касательной прямой CD, меридиональную

плоскость

путем вращения вокруг оси I

поверхности совмещаем с фронтальной

меридиональной плоскостью – главным

меридианом поверхности. Касательная CD

занимает новое положение C*

. S – точка

пересечения касательной с осью I. При обратном

вращении и восстановлении плоскости

точка S

не меняет своего положения, и, следовательно,

искомой фронтальной проекцией касательной

является C

. Касательная плоскость,

заданная АВ ∩ CD = K, является касательной

плоскостью к заданной поверхности в точке К.

Рис. 8.4

Пример 8.2

Построить плоскости, касательные к

поверхности конуса и проходящие через

внешнюю точку A (рис. 8.5).

Плоскости, касательные к конической

поверхности, проходят через вершину конуса, а их

горизонтальные следы касаются основания. Чтобы

касательная плоскость проходила через внешнюю

точку А, она должна содержать прямую SA.

Построив вспомогательную прямую SA,

определим ее горизонтальный след М, через

который проведем касательные прямые m и m*

окружности основания конуса. Касательные m и m*

будут являться горизонтальными следами двух

искомых касательных плоскостей (нулевыми

горизонталями), их фронтальные следы

совпадают с осью координат X.

Рис. 8.5

C*2

C*1

S1=I1

Ï1

122

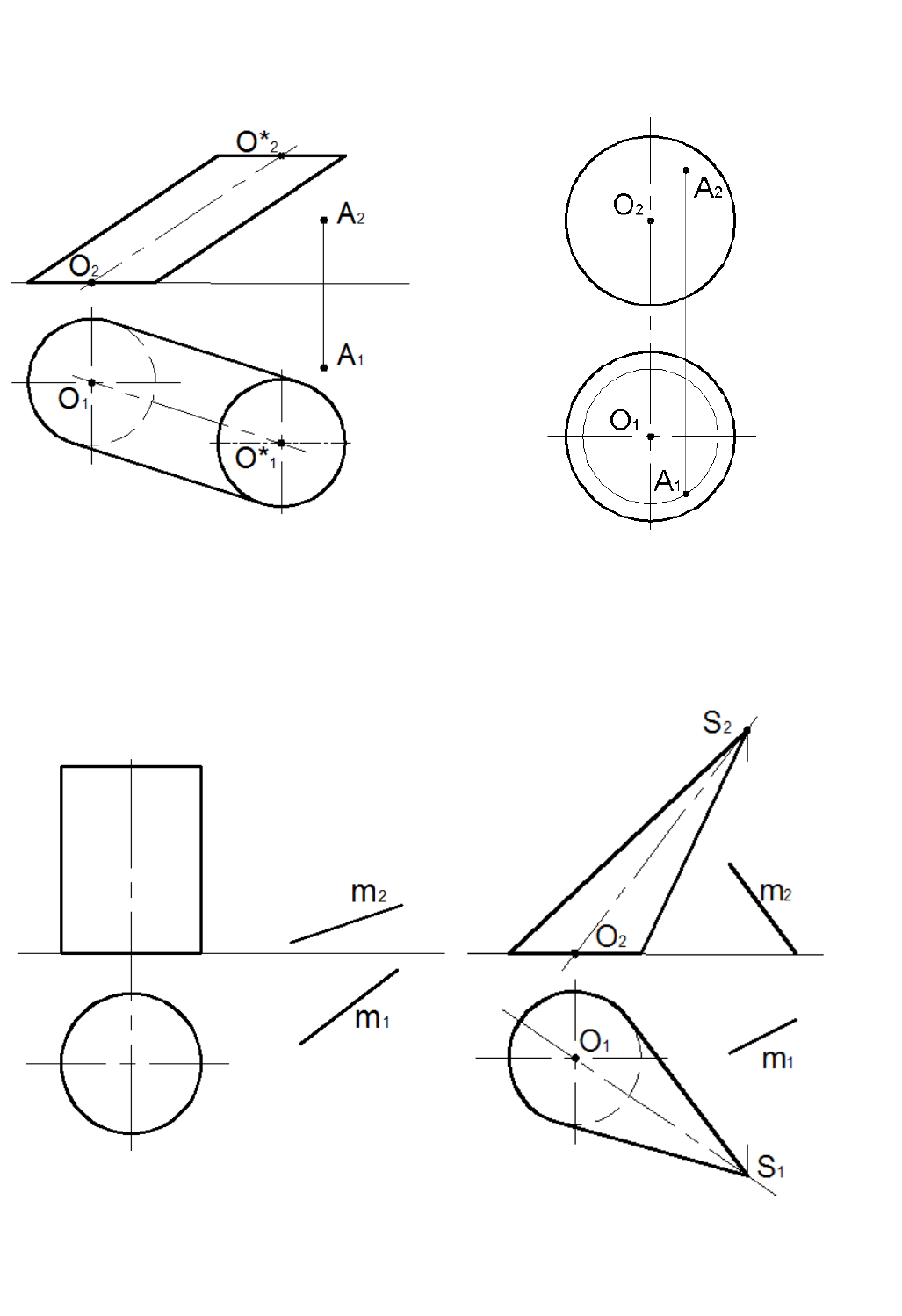
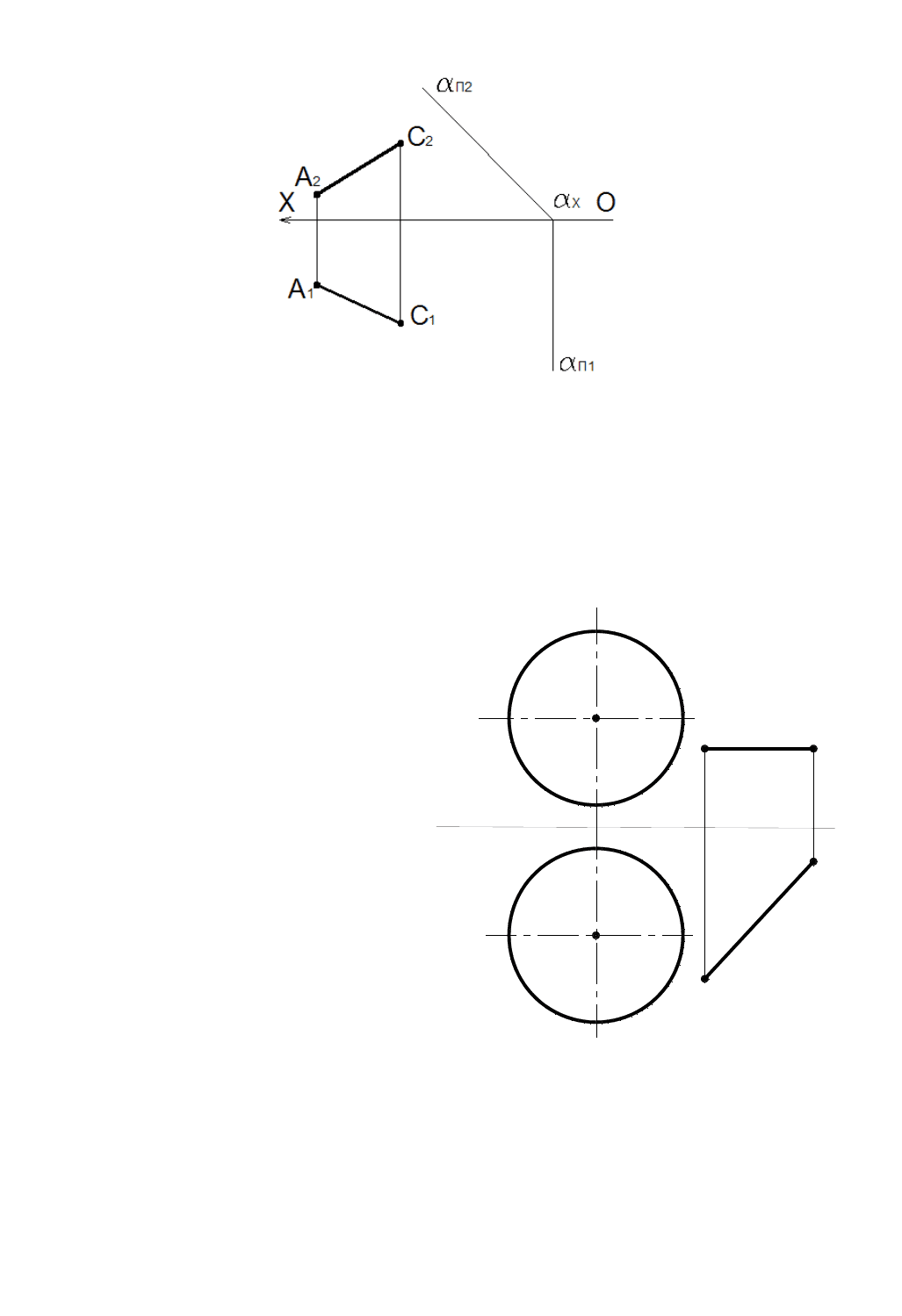
Задача 8.1

Построить плоскость, касательную к

поверхности цилиндра и проходящую через

внешнюю точку A.

Задача 8.2

Построить плоскость, касательную к сфере

в точке A.

Рис. 8.6 Рисс. 8.7

Задача 8.3

Построить плоскость, параллельную прямой

m и касательную к поверхности цилиндра.

Задача 8.4

Построить плоскость, касательную к

поверхности цилиндра и проходящую через

внешнюю точку A.

Рис. 8.8 Рис. 8.9

123

9. Комплексные задачи

Задача 9.1

В плоскости

(А, В, С) построить точку, равноудаленную от точек A, В, С.

Рис. 9.1

124

Задача 9.2

Найти на отрезке прямой АВ точку, равноудаленную от сторон линейного угла CDE.

Рис. 9.2

Задача 9.3

Построить проекции шара с центром на отрезке АВ, касающегося отрезка СD на расстоянии

20 мм от плоскости П

Рис.9.3

125

Задача 9.4

Построить проекции шара радиусом 40 мм, касающегося плоскости

в точке К. Построить проекции

сечения шара горизонтально-проецирующей плоскостью

(

= 45 º), проходящей через точку К.

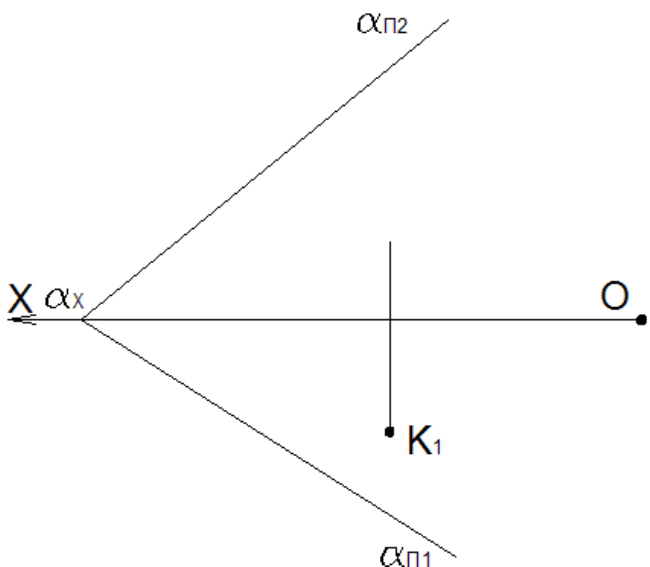
Рис. 9.4

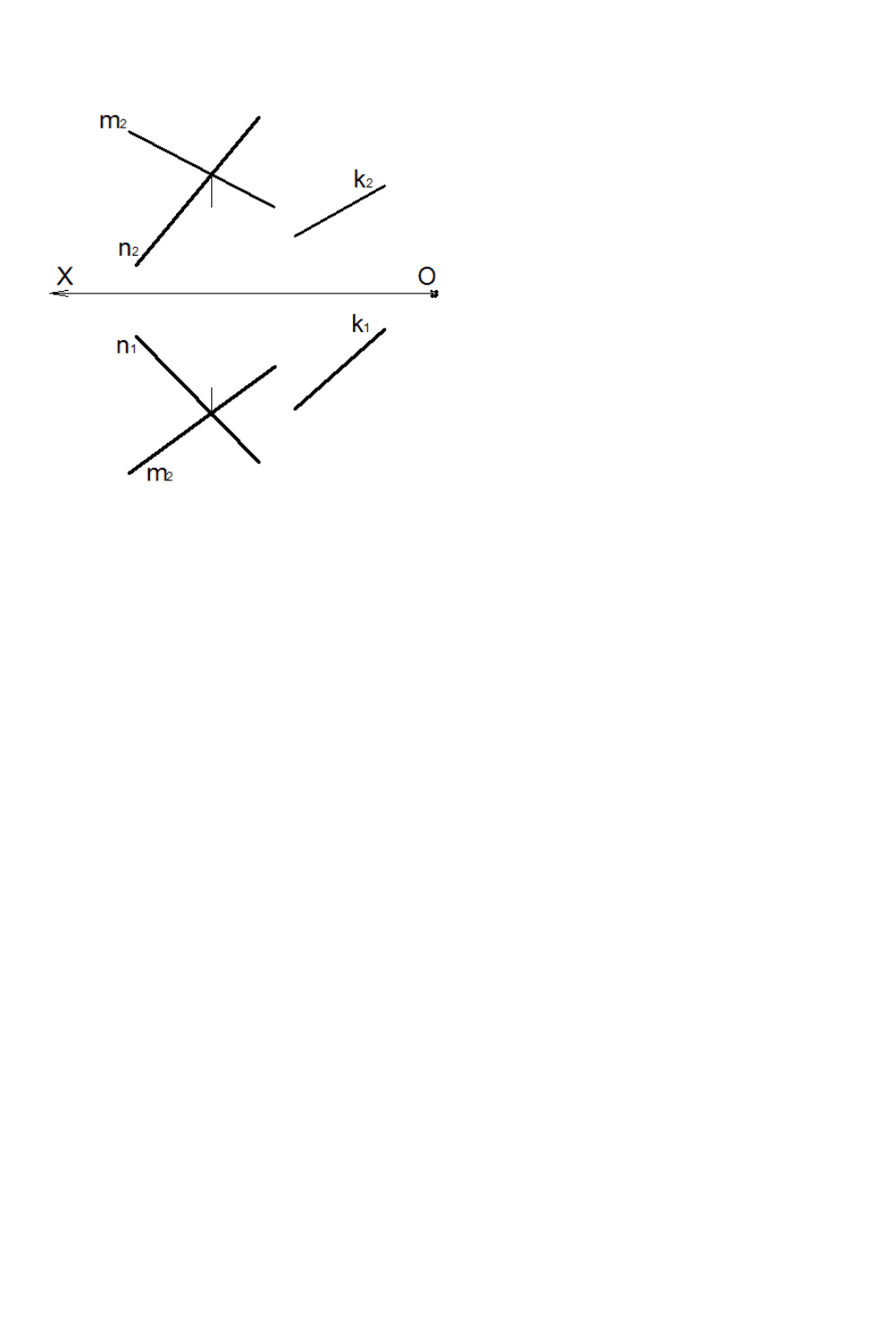
126

Задача 9.5

Провести плоскость, параллельную плоскости

, заданную пересекающимися прямыми

(m ∩ n)

так, чтобы отрезок прямой k, заключенный между двумя плоскостями, был равен 30 мм.

Рис. 9.5

127

Задача 9.6

Достроить проекции ромба ABCD, если диагональ BD параллельна плоскости

, а вершина B

расположена в плоскости П

Рис. 9.6

Задача 9.7

Через отрезок прямой АВ провести плоскость, которая пересекает сферу с центром в точке О по

окружности радиусом 15 мм.

Рис. 9.7

128

Задача 9.8

Через точку М провести плоскость, параллельную отрезку АВ и перпендикулярную плоскости

треугольника ADEF. Плоскость задать треугольником и определить его натуральную величину.

Рис. 9.8

129

Для самостоятельной работы