Понетаева Н.Х., Патрушева Н.В. Начертательная геометрия в примерах и задачах
Подождите немного. Документ загружается.

58
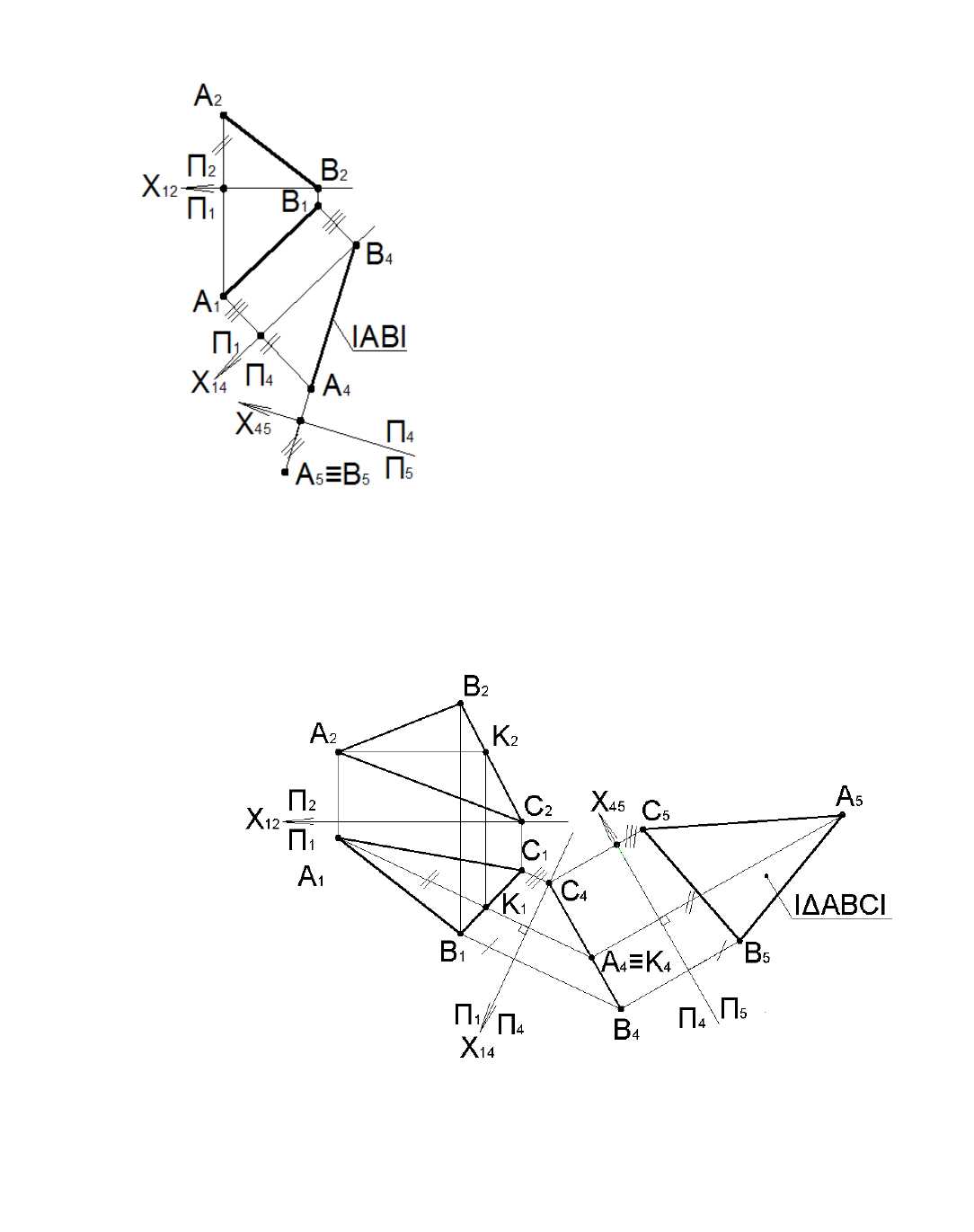
Пример 4.1
Перевести отрезок прямой АВ общего положения в проецирующее.
Первая замена плоскостей проекций.
Перейдем от системы плоскостей П
1
⊥П
2
к системе
П
1
⊥П
4
, заменив П
2
на П
4
так, чтобы АВ||П
4
Новая ось
Х
14
проведена параллельно проекции А
1
B
1
, при этом
П
4
‖АВ. Из А
1
и В
1
перпендикулярно Х
14
проведем
линии проекционной связи, на них отложим отрезки,
равные Z
A
и Z
B
. Получим новую проекцию, равную
натуральной величине отрезка А
4
В
4
=|АВ|.
Вторая замена плоскостей проекций.
Плоскость П
1
заменяем на П
5
так, чтобы отрезок АВ
стал проецирующим: АВ⊥П
6
. Для этого проведем
новую ось Х
45
перпендикулярно А
4
В
4
и на линии
проекционной связи, являющейся продолжением
проекции отрезка А
4
В
4
, отложим отрезки, равные
расстояниям от заменяемых проекций А
1
и В
1
до
заменяемой оси координат Х
14
. Так как эти отрезки
равны, то получаем одну точку А
5
=В
5
, являющуюся
проекцией отрезка AВ на плоскость П
5
.
Рис. 4.3
Пример 4.2
Найти натуральную величину треугольника ABC и угол наклона его плоскости к горизонтальной
плоскости проекций П
1
.
Рис. 4.4
Выберем новую плоскость проекций П
4
, перпендикулярную плоскости треугольника ABC, а на
комплексном чертеже – перпендикулярную горизонтали АК плоскости треугольника: П
4
⊥ ΔАВС, П
4
⊥ АК,
АК ∈ΔАВС, АК || П
1.
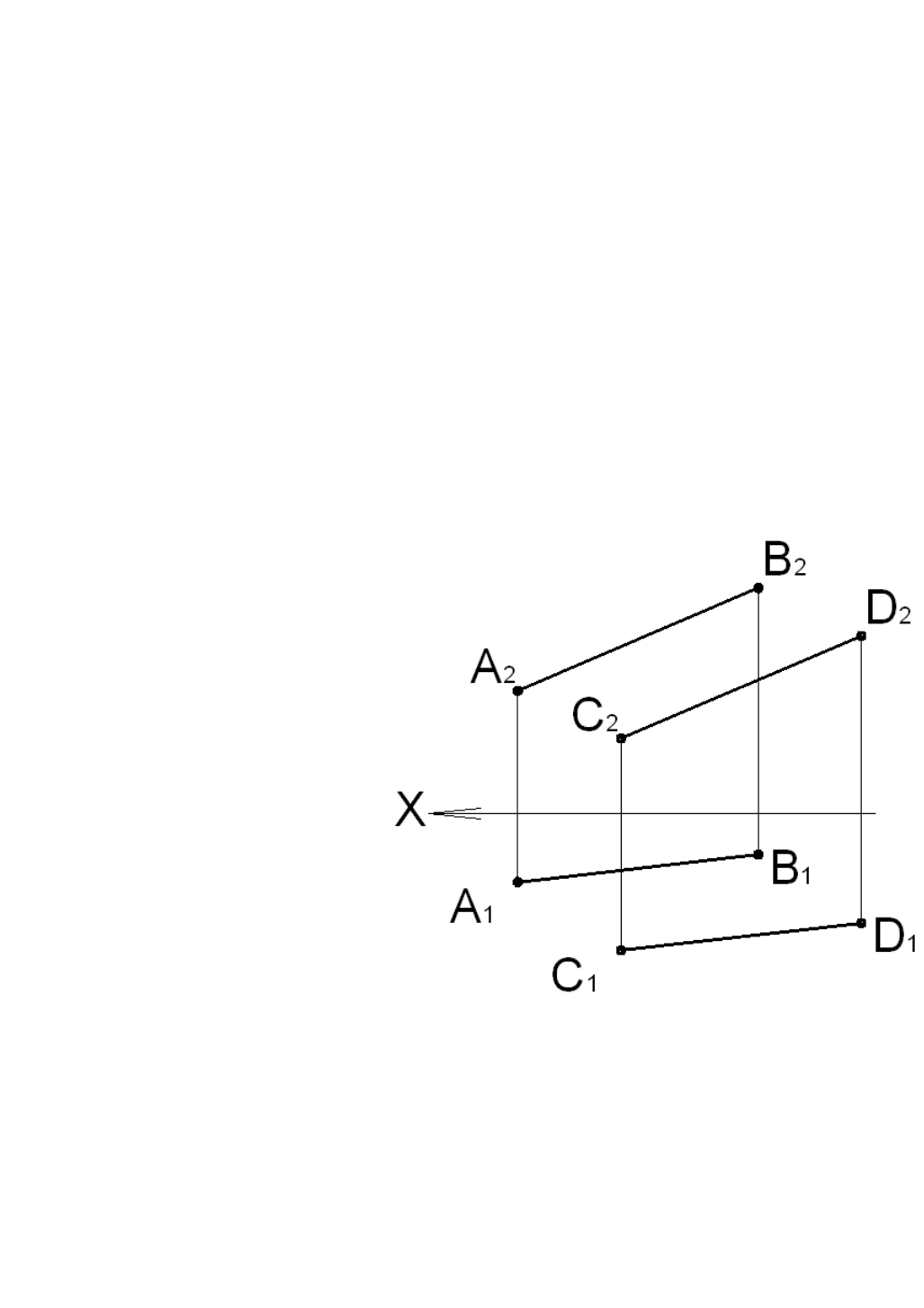
59
Проводим новую ось координат Х
14
перпендикулярно А
1
К
1
: Х
14
⊥ А
1
К
1
.Имеем систему взаимно
перпендикулярных плоскостей П
1
⊥ П
4
. Плоскость треугольника ABC по отношению к плоскости П
4
будет
проецирующей. Проводим линии проекционной связи от точек А
1
, В
1
, С
1
и откладываем координаты Z вершин
треугольника от новой оси Х
14
, получаем проекции точек А
4
, В
4
, С
4
. Проекция треугольника ABC на П
4
– прямая
С
4
В
4
, составляющая с осью Х
14
угол, равный натуральной величине угла между плоскостью треугольника и П
1
– угол
ϕ
.
Чтобы найти натуральную величину треугольника вместо плоскости П
1
вводим новую плоскость П
5
,
параллельную плоскости треугольника. Параллельно вырожденной проекции треугольника С
4
В
4
проводим новую
ось Х
45
. На линиях проекционной связи отложим от новой оси отрезки, равные расстояниям от заменяемых
проекций вершин A
1
B
1
С
1
до заменяемой оси Х
14
.
А
5
В
5
С
5
– натуральная величина треугольника.
Задача 4.1
Найти расстояние между параллельными прямыми АВ и CD.
Рис. 4.5
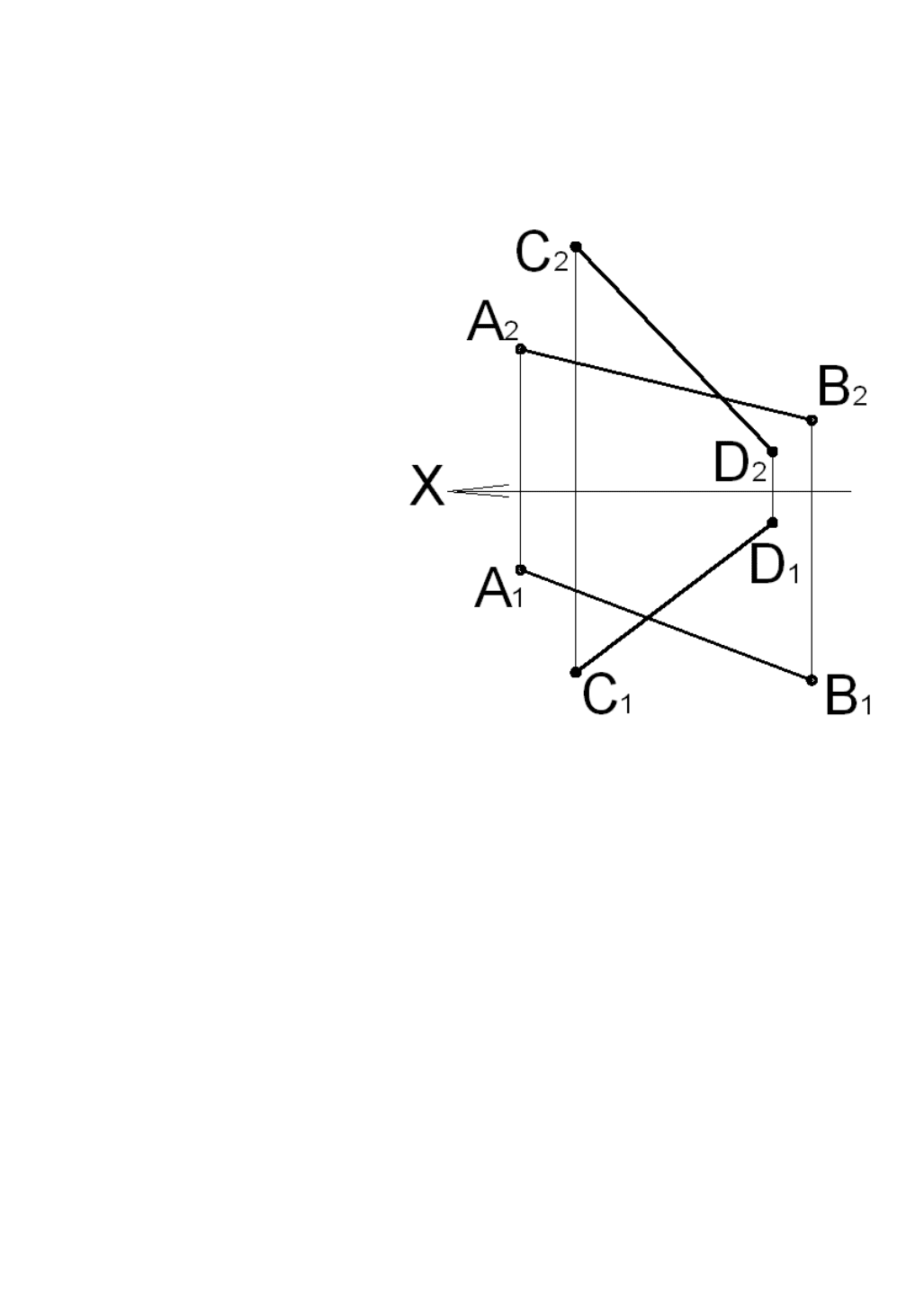
60
Задача 4.2
Найти расстояние между скрещивающимися прямыми АВ и CD.
Рис. 4.6
61
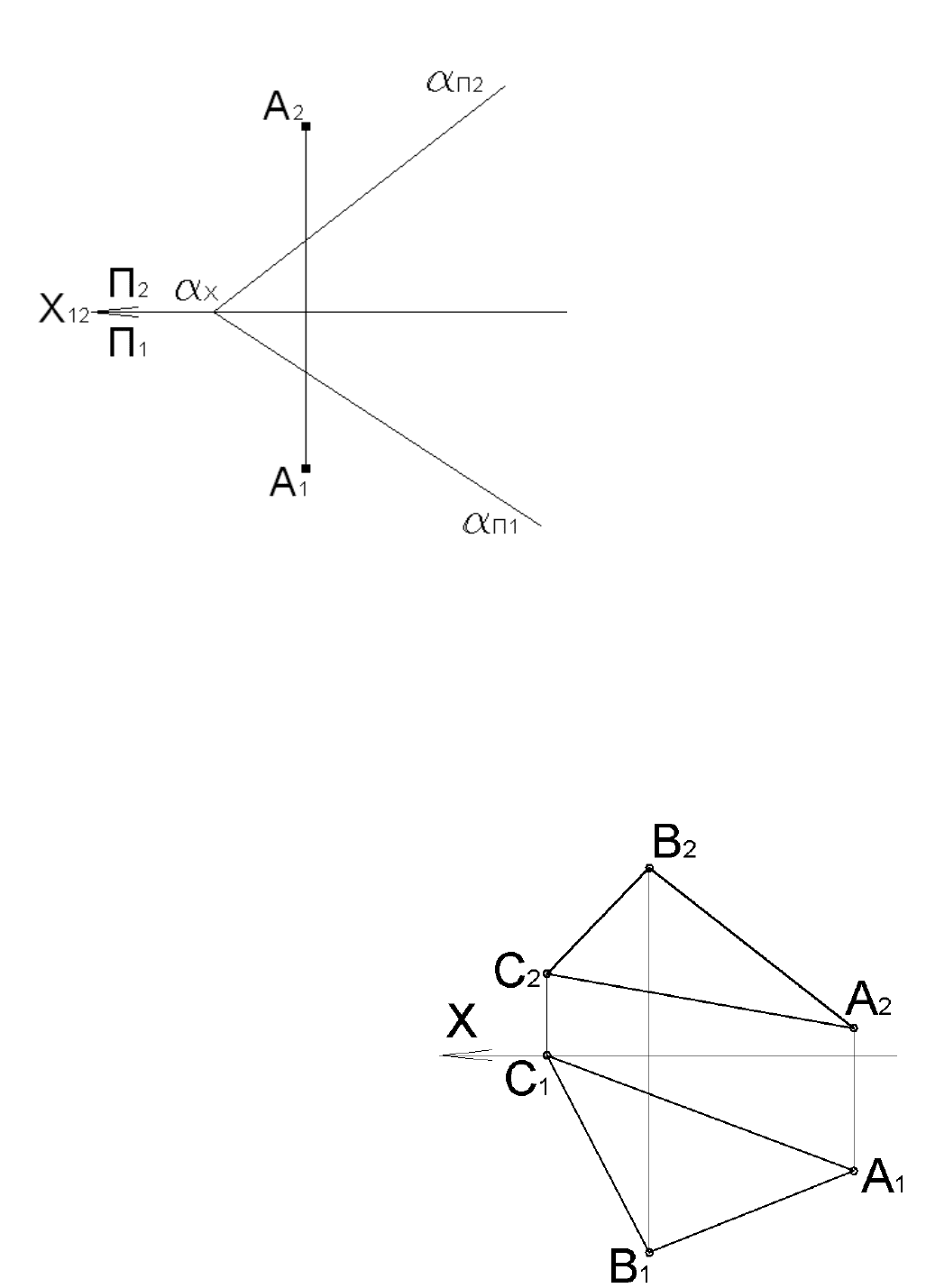
Задача 4.3
Найти расстояние от точки А до плоскости
α
.
Рис. 4.7
Задача 4.4
Найти точку M, принадлежащую треугольнику ABC, расположенную на расстоянии 10 мм от сторон АB и
BC.
Рис. 4.8
62
4.2 Плоскопараллельное перемещение
Плоскопараллельным перемещением в пространстве называется такое перемещение, при котором все
точки геометрической фигуры перемещаются во взаимно параллельных плоскостях без изменения вида и
размеров этой фигуры.
При перемещении величины проекций не изменяются, следовательно, сохраняется угол наклона
геометрической фигуры (прямых, плоскостей) к данной плоскости проекций.
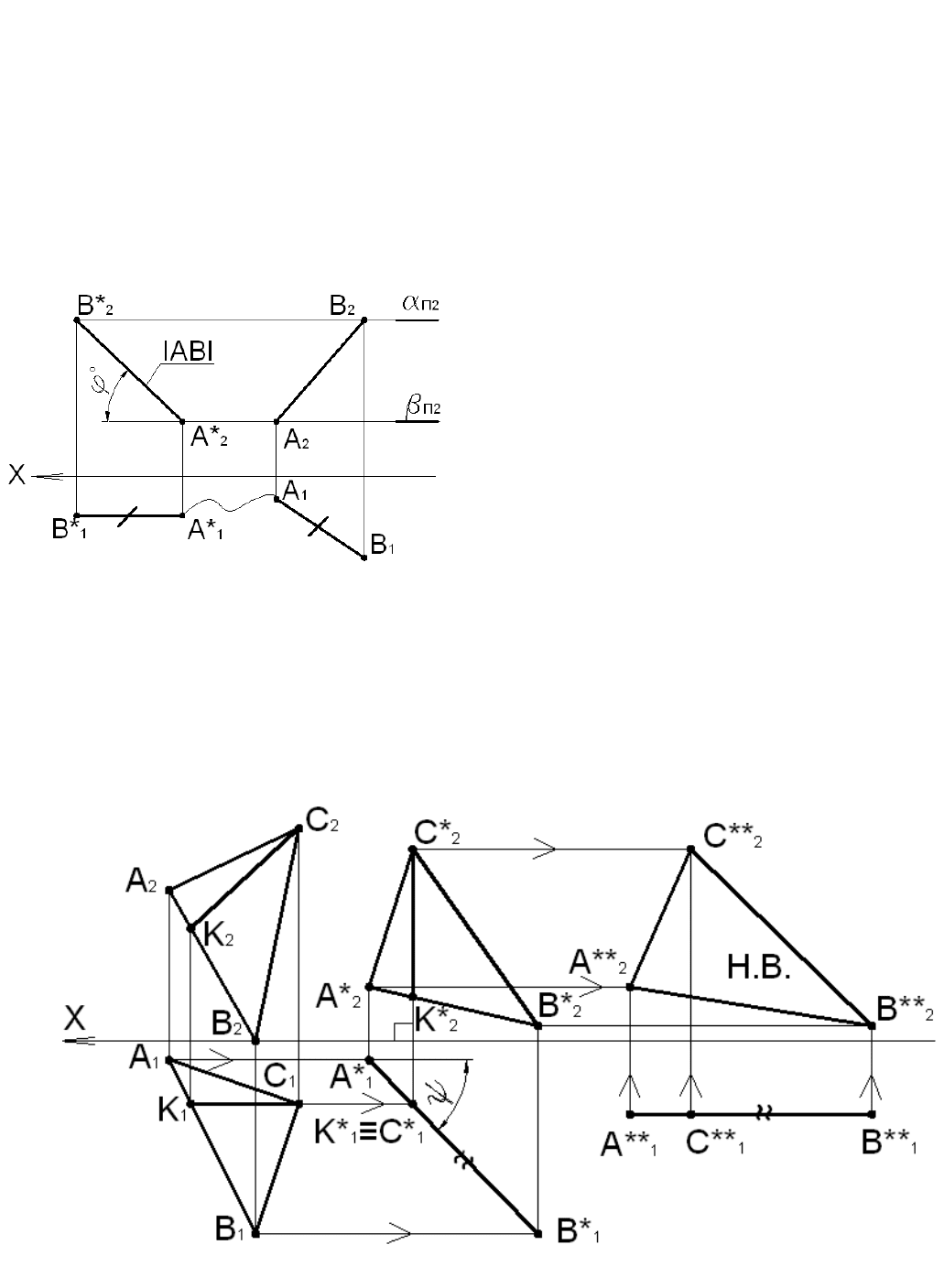
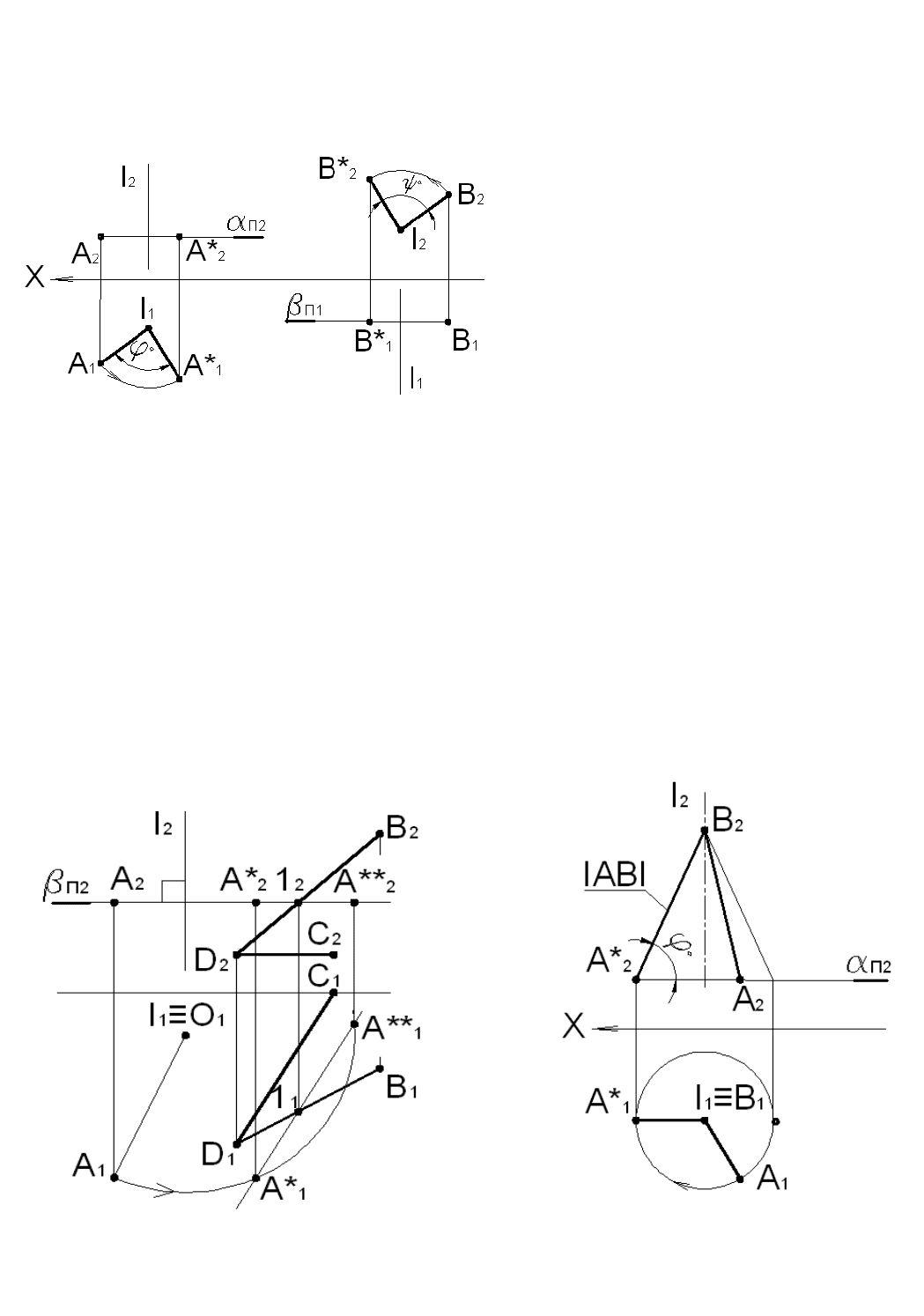
Пример 4.3
Прямую общего положения АВ преобразовать во фронталь и определить ее натуральную
величину и угол наклона к горизонтальной плоскости проекций П
1
.
Перемещением переводим отрезок прямой AB
В положение, параллельное фронтальной плоскости
проекций П
2
. Для этого в произвольном месте
чертежа горизонтальную проекцию А
1
В
1
отрезка AB
располагаем горизонтально, параллельно оси
координат ОХ;
A*
1
B*
1
‖OX, А*
1
В*
1
=А
1
В
1
.
Точки A и B отрезка перемещаются
соответственно в горизонтальных плоскостях αиβ:
А∈α ∧ α || П
1
, В ∈ β ∧ β || П
1
.
Фронтальные проекции A
2
и B
2
точек A и B
перемещаются по
α
П2
и
β
П2
(Z
A
= const, Z
B
= const).
Фронтальные проекции A*
2
и B*
2
смещенных точек
A* и B* находятся в проекционной связи с
проекциями A*
1
и B*
1
.
A*
2
B*
2
– новая фронтальная проекция отрезка
AB: A*
2
B*
2
= | AB|.
Угол наклона A*
2
B*
2
к оси OX является
натуральной величиной угла наклона отрезка AB к
плоскости проекций П
1
: A*
2
B*
2
^OX = AB ^ П
1
.
Рис. 4.8
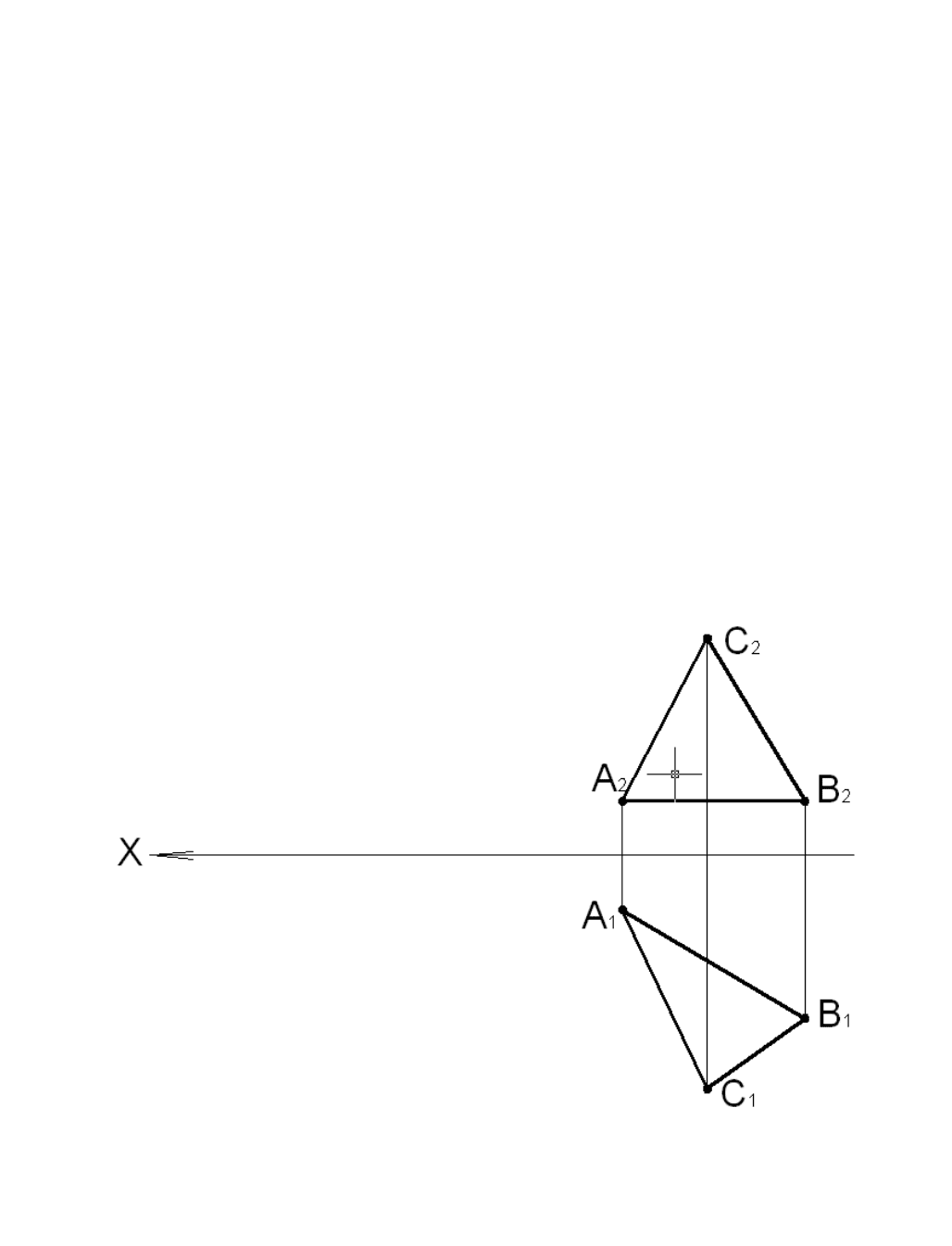
Пример 4.4
Определить натуральную величину треугольника ABC и угол его наклона к плоскости проекций П
2
.
Рис. 4.9
63
Задача решается двумя последовательными перемещениями. Первым перемещением треугольник
ABC приводится в положение, перпендикулярное горизонтальной плоскости проекций П
1
. Вторым
перемещением этот треугольник приводится в положение, параллельное фронтальной плоскости проекций П
2
.
Для этого в плоскости треугольника ABC проводим фронталь ВК. Перемещаем фронталь ВК в
положение горизонтально проецирующей прямой: ВК ⊥ П
1
. При этом плоскость треугольника станет
горизонтально проецирующей плоскостью. На чертеже проводим следующие построения. Фронтальную
проекцию В
2
K
2
располагаем перпендикулярно оси координат ОХ. Величина фронтальной проекции
треугольника при этом не меняется. Строим фронтальную проекцию треугольника А*
2
В*
2
С*
2
, учитывая
равенство сторон:
A
2
B
2
= A*
2
B*
2
, А
2
С
2
= A*
2
С*
2
, В
2
С
2
= В*
2
С*
2
.
Горизонтальной проекцией А
1
В
1
С
1
треугольника в новом положении является отрезок прямой А*
1
C*
1
, угол
наклона которого к оси ОХ является натуральной величиной угла наклона плоскости треугольника к плоскости
П
2
– угол
ψ
.
Чтобы получить натуральную величину треугольника, переместим вырожденную горизонтальную
проекцию треугольника (прямая А*
1
С*
1
,) на свободное место чертежа в положение, параллельное оси ОХ.
Плоскость треугольника станет плоскостью уровня. Фронтальные проекции точек при этом перемещаются
параллельно оси ОХ (сохраняется неизменной координата Z точек). На фронтальной проекции имеем
натуральную величину плоскости треугольника ABC:
А**
2
В**
2
С**
2
= | Δ АВС|.
Задача 4.4
Определить натуральную величину треугольника ABC и угол его наклона к горизонтальной плоскости
проекций П
1
.
Рис. 4.10
64
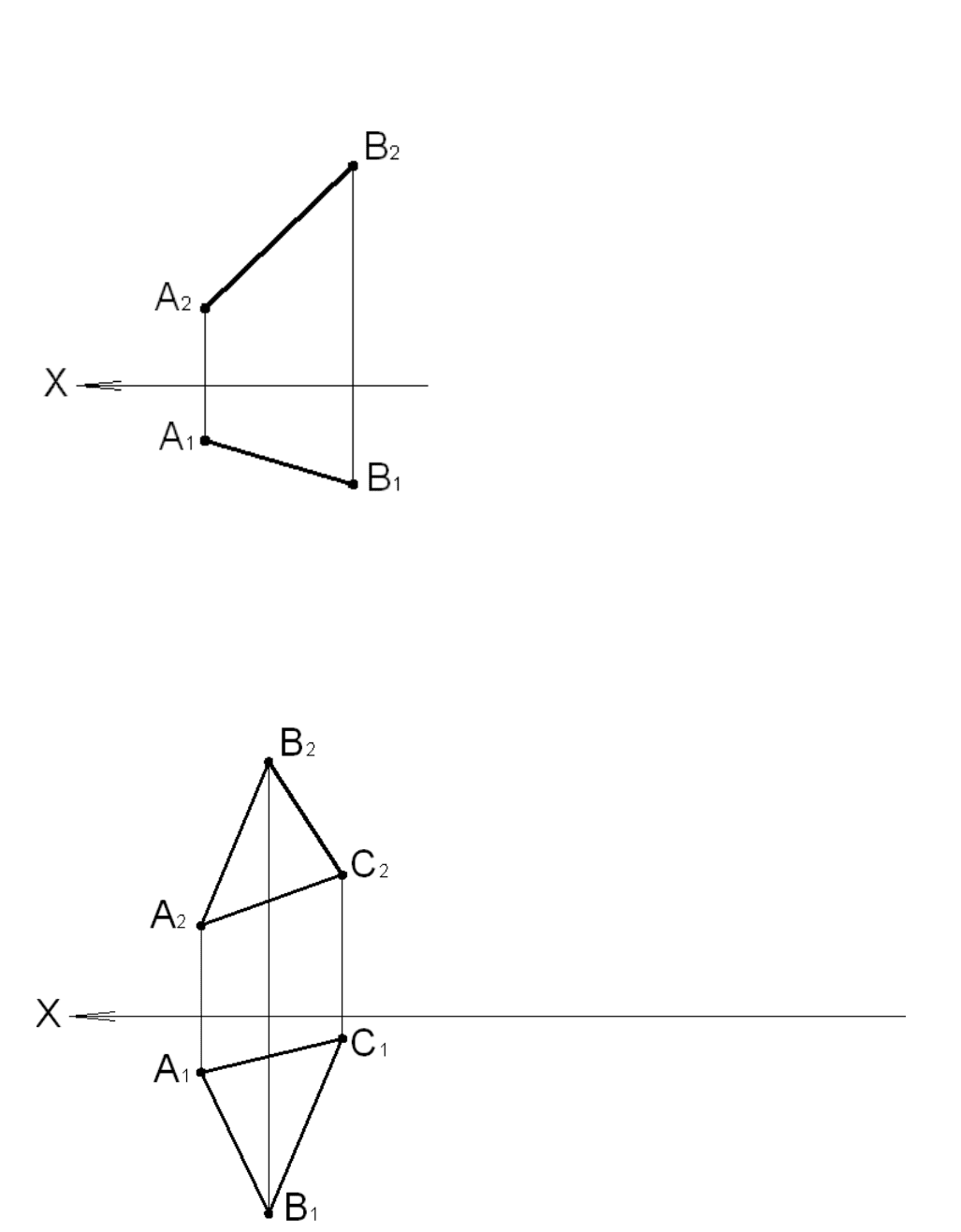
Задача 4.5
Найти натуральную величину отрезка прямой АВ и угол наклона отрезка к фронтальной плоскости
проекций П
2
.
Рис. 4.11
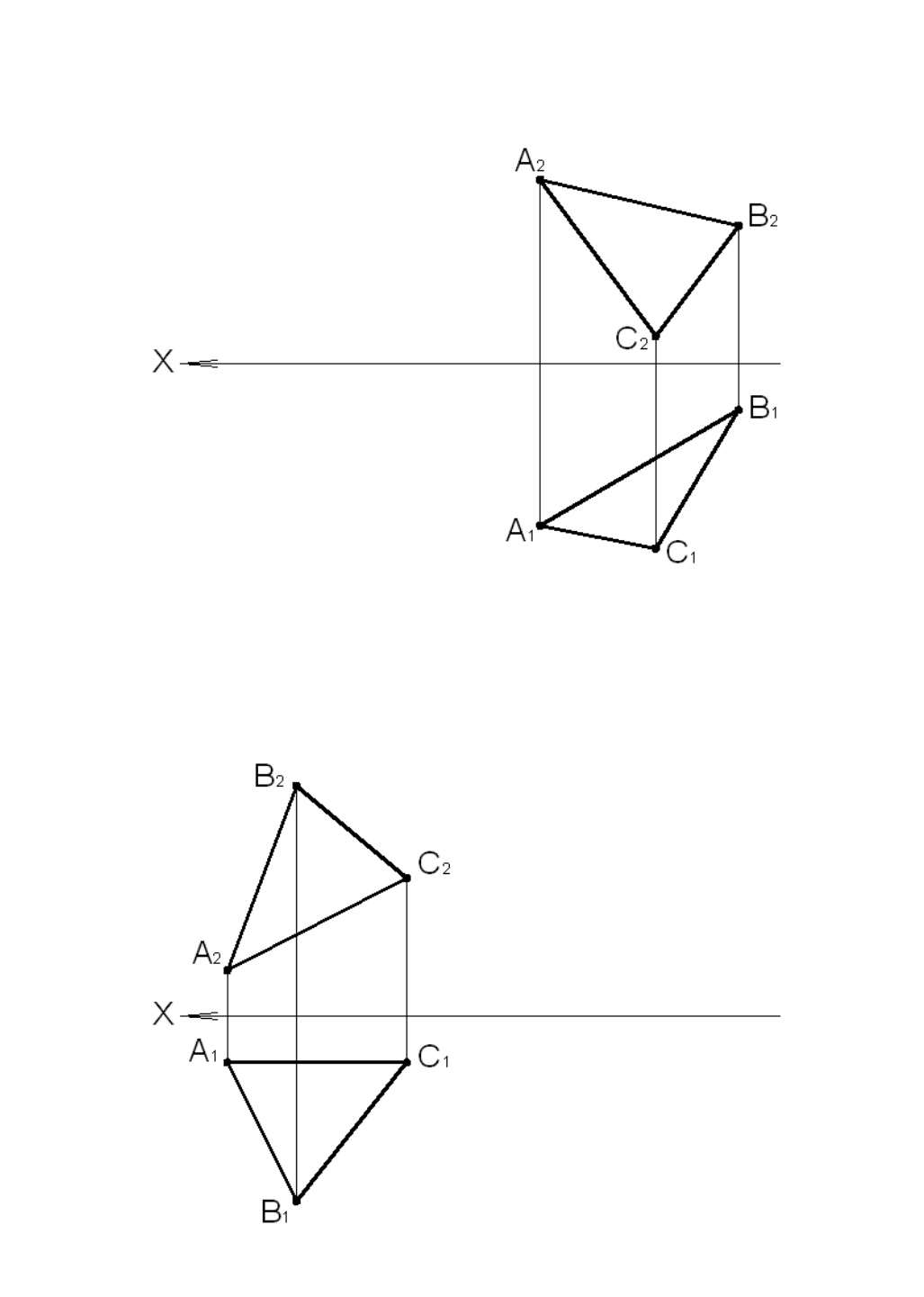
Задача 4.6
Найти расстояние от точки С до стороны АВ треугольника ABC.
Рис. 4.12
65
Задача 4.7
Определить центр описанной около треугольника ABC окружности.
Рис. 4.13
Задача 4.8
В треугольнике ABC найти точку М, удаленную от сторон АВ и ВС на расстояние 15 мм.
Рис.4.14
66
4.3. Вращение вокруг проецирующих прямых
Этот способ является частным случаем способа плоскопараллельного перемещения. В способе
плоскопараллельного перемещения точка описывает некоторую плоскую кривую, параллельную плоскости
проекций, а при вращении вокруг проецирующих прямых точка описывает дугу окружности, плоскость
которой также параллельна плоскости проекций.
При повороте точки А вокруг
горизонтально проецирующей оси I⊥П
1
, на
угол ϕ против часовой стрелки (рис.4.15) точка А
перемещается в плоскости
α
⊥I ∧
α
‖П
1
по
окружности радиуса R
A
=I
1
A
1
. Горизонтальная
проекция точки А
1
описывает дугу А
1
A*
1
окружности радиуса R
A
с центральным углом
ϕ
.
Фронтальная проекция точки А
2
движется по
прямой, параллельной оси координат OX
(Z
A
=const). Зная новое положение А*
1
определяем ее фронтальную проекцию А*
2
.
На рис. 4,16 показан поворот точки В
вокруг фронтально проецирующей оси на угол
ψ
против часовой стрелки:
I ⊥П
2
, В∈
β
⊥I ∧
β
||П
2
, R
B
=I
2
B
2
, Y
B
=const.
Рис. 4.15 Рис. 4.16
Пример 4.5
Точку А повернуть вокруг горизонтально проецирующей оси до совмещения c плоскостью, заданной
пересекающимися прямыми BD и CD -
α
(BD∩CD) (рис. 4.17).
При вращении вокруг горизонтально проецирующей оси точка А движется по окружности в плоскости
β
⊥I ∧
β
||П
1
.Центром вращения является точка O =
β
∩ l, радиус вращения – R
A
=O
1
A
1
.
Новые положения точек А *и А** определяются на пересечении дуги окружности и горизонтали, по
которой пересекаются плоскости
α
и
β
.
Вращение прямой вокруг оси, пересекающей эту прямую, сводится к вращению какой-либо одной ее
точки, поскольку точка пересечения прямой с осью вращения остается неподвижной.
На рис. 4.18 отрезок AB общего положения вращением
вокруг оси I
⊥
П
1
∧ B
∈
I приведен в положение,
параллельное фронтальной плоскости проекций П
2
:
A*
2
B
2
⎜⎜П
2
, A*
2
B
2
=⎮AB⎮.
Рис. 4.17 Рис. 4.18
Если ось вращения не пересекает прямую, то вращение осуществляется путем поворота двух точек
прямой на один и тот же угол и в одном и том же направлении
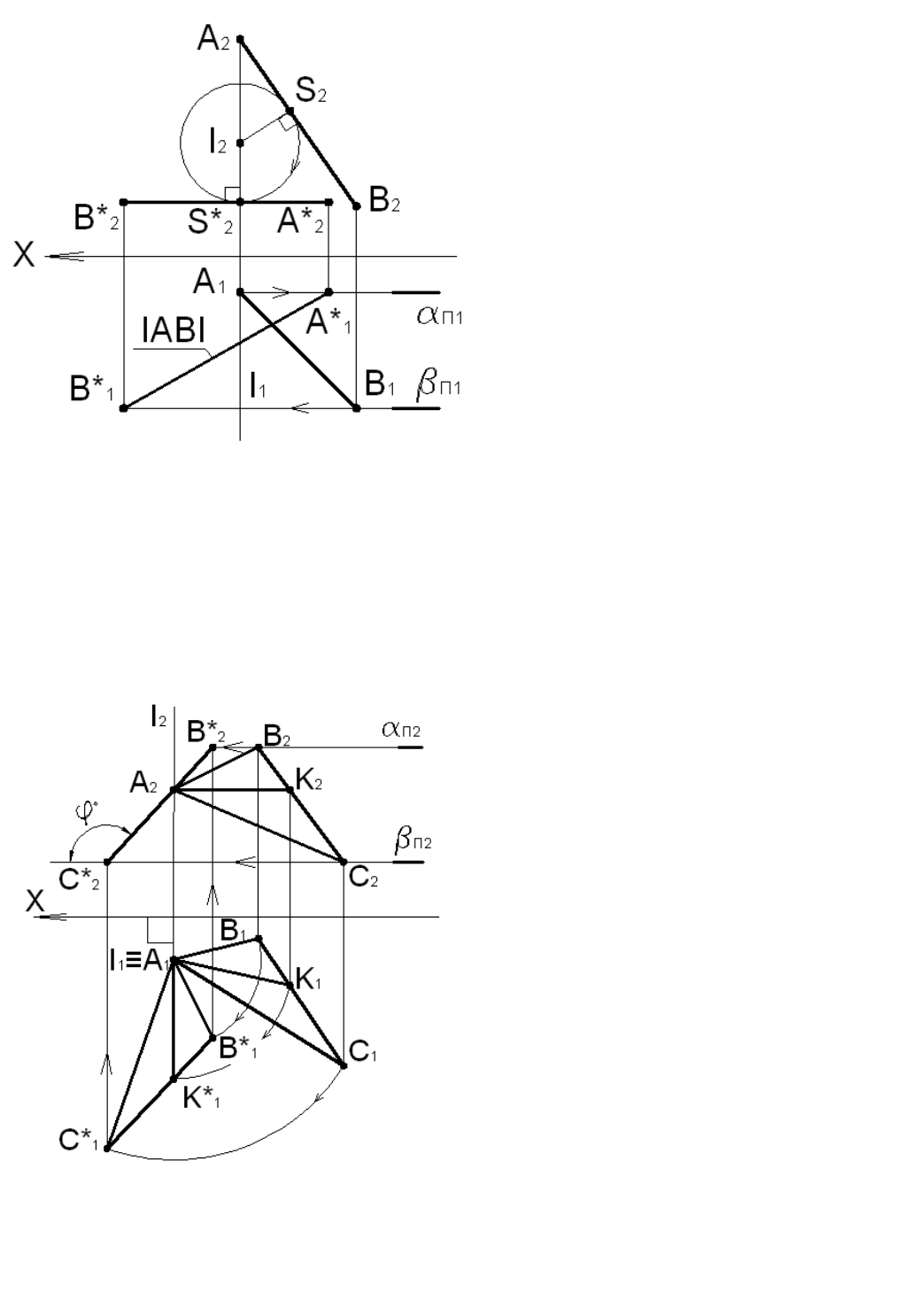
67
Пример 4.6
Отрезок АВ прямой общего положения
повернуть вокруг фронтально проецирующей
оси в положение горизонтали.
Проекция вращаемого отрезка на плоскость,
которой перпендикулярна ось вращения, не
изменяется. Поэтому можно вращать одну точку.
Удобно вращать точку S
2
– основание
перпендикуляра, опущенного из точки I
2
на
фронтальную проекцию прямой А
2
В
2
. I
2
–
фронтальная проекция оси вращения I
⊥
П
2
.
Когда радиус вращения I
2
S
2
⊥ OX, прямая AB
II П
1
∧ A*
1
B*
1
= I AB I.
Рис. 4.19
Вращение плоскости вокруг оси, перпендикулярной плоскости проекций, осуществляется путем
вращения на один и тот же угол и в одном и том же направлении трех точек и прямых, которыми задана
плоскость.
Пример 4.7.
Определить угол наклона ϕ плоскости DABC общего положения к горизонтальной
плоскости проекций П
1
Плоскость
Δ
АВС перпендикулярна
фронтальной плоскости проекций П
2
, если
горизонталь треугольника перпендикулярна
фронтальной плоскости проекций.
Проводим в плоскости треугольника ABC
горизонталь АК и вращаем треугольник вокруг
горизонтально проецирующей оси А ∈ I⊥П
1
. В этом
случае угол наклона плоскости DАВС к
горизонтальной плоскости проекций П
1
остается
постоянным
ϕ
=const, а угол наклона к П
2
меняется.
Повернем треугольник ABC так, чтобы
горизонталь АК заняла положение,
перпендикулярное оси координат ОХ:
АК∈DАВС^АК‖П
1
,А
1
K*
1
⊥ОХ.
Горизонтальная проекция треугольника,
переместившись на тот же угол, что и проекция А
1
К
1
горизонтали АК, займет положение А
1
B*
1
C*
1
.
Фронтальные проекции В
2
и С
2
перемещаются по
горизонтальным прямым – фронтальным следам
α
П2
и
β
П2
плоскостей движения точек В и С,
Z
B
=const, Z
C
=const. B
2
и С
2
определяем по линиям
проекционной связи на соответствующих следах
плоскостей
α
и
β
. Соединив B*
2
А
2
С*
2
, получаем
прямую, в которую выродился Δ ABC после
поворота.
Рис. 4.20
