Понетаева Н.Х., Патрушева Н.В. Начертательная геометрия в примерах и задачах
Подождите немного. Документ загружается.

110
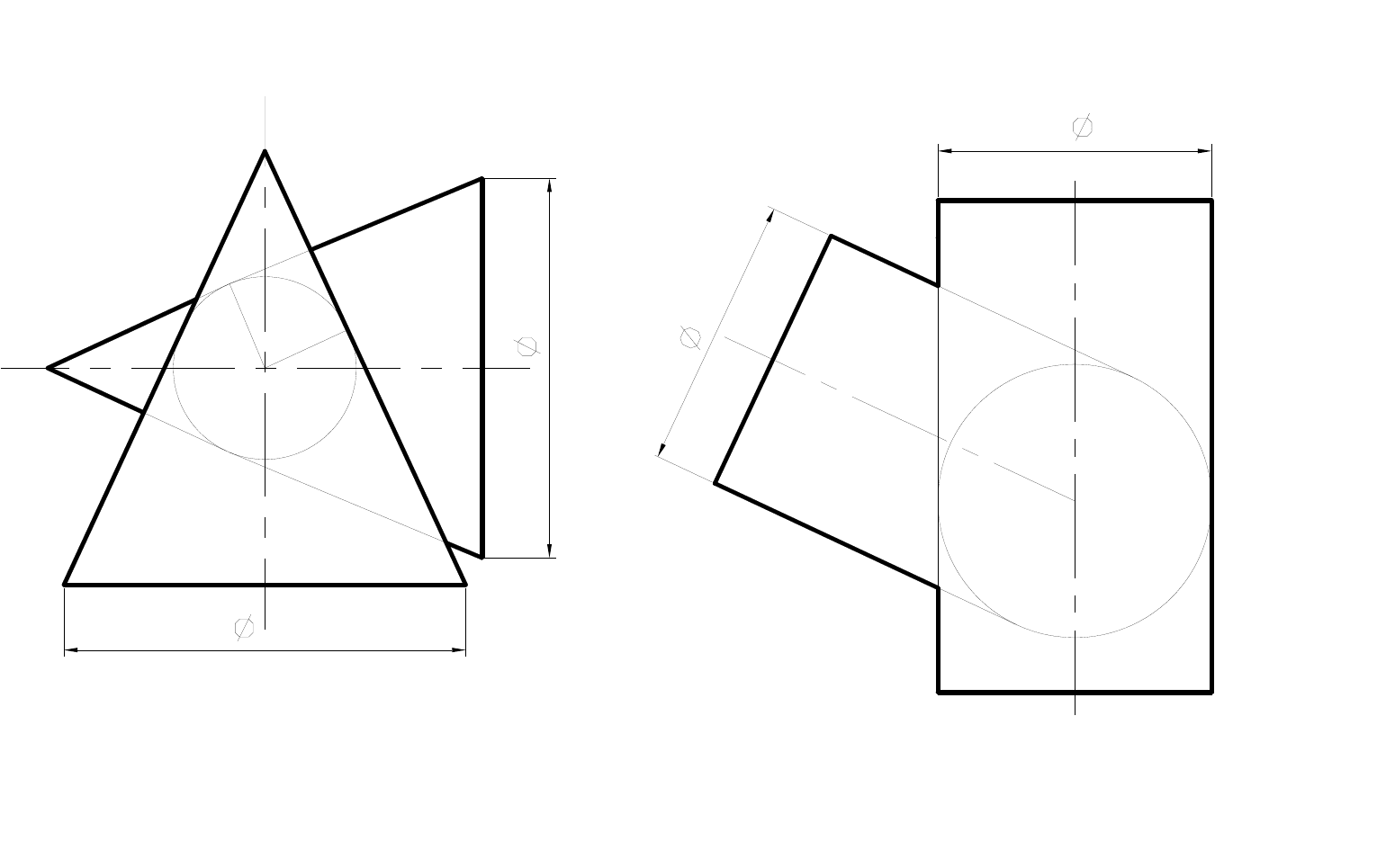
Задача 6.15
Построить проекцию линии пересечения конуса и цилиндра,
описанных около одной сферы.
Задача 6.16
Построить проекцию линии пересечения цилиндров, описанных около
одной сферы.
Рис. 6.23
Рис. 6.24
111
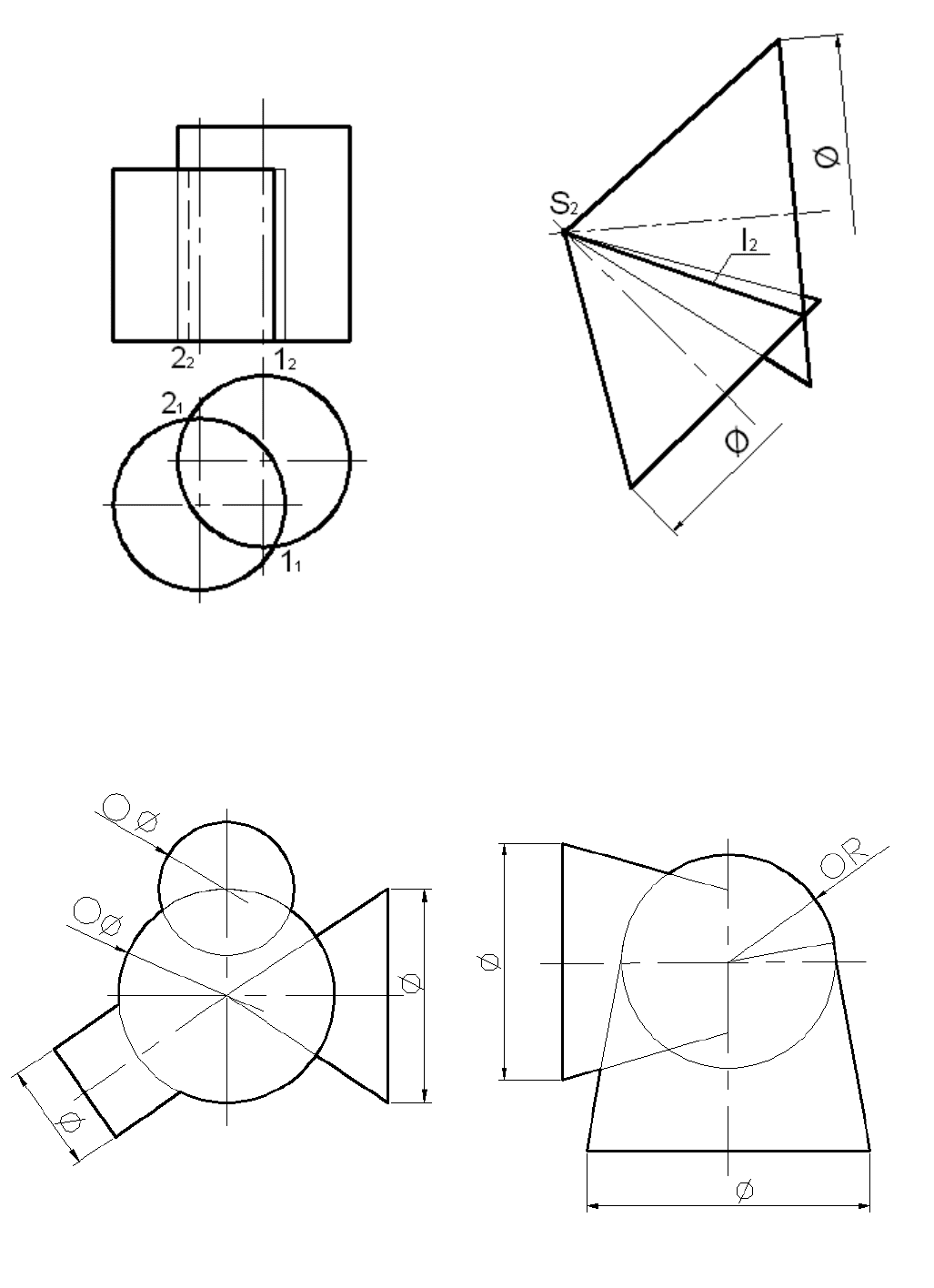
6.4.2. Цилиндры с параллельными осями
пересекаются по образующим.
6.4.3. Конусы с общей вершиной пересекаются
по образующим.
Рис. 6.25
Рис. 6.26
Задача 6.17
Построить проекцию линии пересечения
поверхностей с общей осью.
Задача 6.18
Построить проекцию линии пересечения
поверхностей
Рис. 6.27 Рис. 6.28
112
Для самостоятельной работы
113
7. Развертка поверхностей
Разверткой называется фигура, полученная при совмещении поверхности с плоскостью без складок
и разрывов.
Развертку боковой поверхности прямого кругового конуса заменяют разверткой боковой
поверхности прямой правильной многоугольной пирамиды, вписанной в конус.
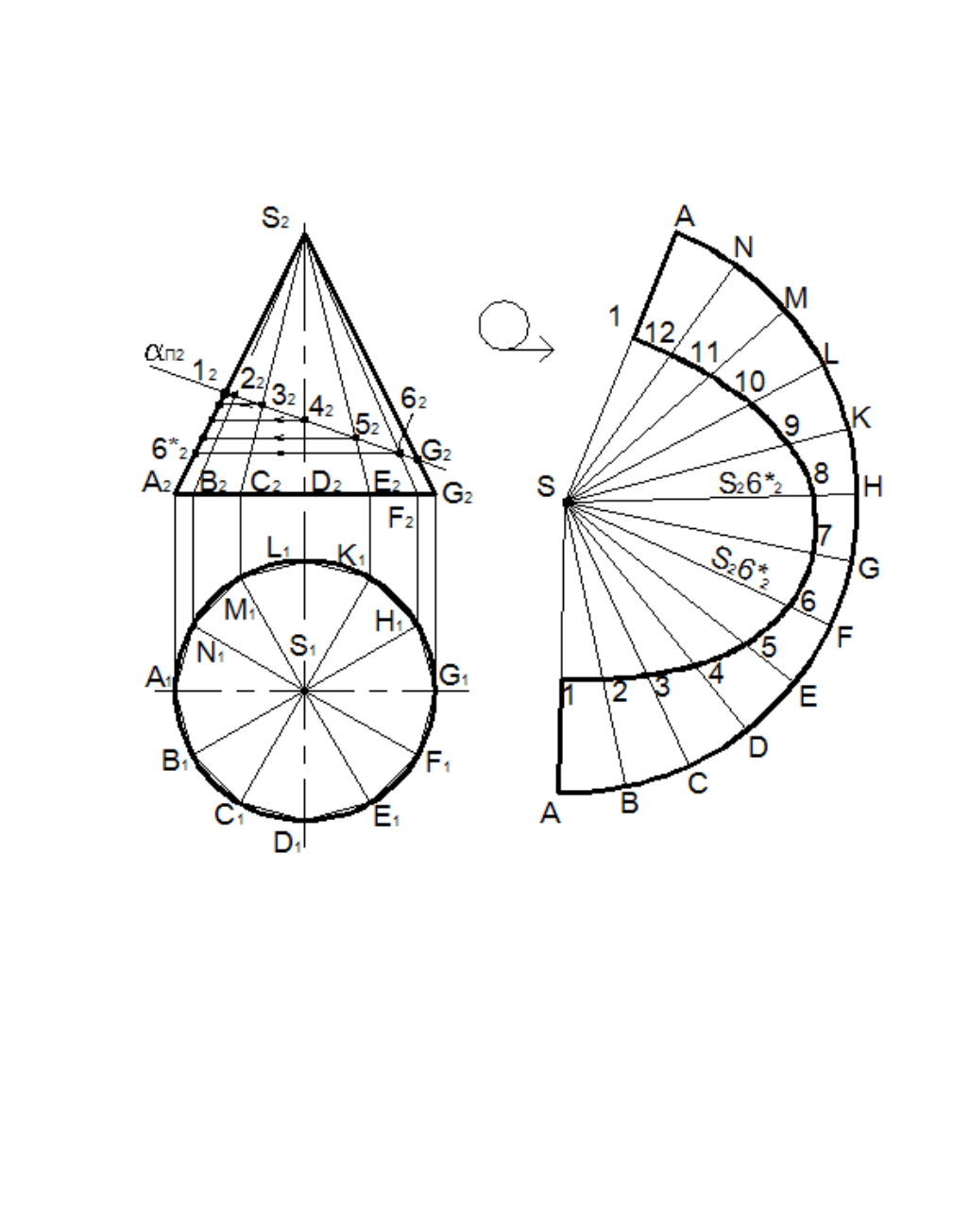
Пример 7.1
Построить развертку боковой поверхности кругового конуса, усеченного плоскостью
α
.
Рис. 7.1
Делим основание конуса на 12 частей и проводим через точки деления образующие конуса, находим
точки их пересечения с плоскостью
α
.
Строим развертку боковой поверхности полного конуса.
Из произвольной точки S на свободном поле чертежа проводим дугу радиусом, равным длине
образующей конуса. Засекаем последовательно от произвольной точки A 12 дуг, хорды которых равны
стороне 12-угольника, вписанного в основание конуса. Проводим образующие конуса. На каждой
образующей откладываем натуральную величину длины отрезка соответствующей образующей
конуса от его вершины до точки пересечения с плоскостью
α
. Натуральная величина отрезков образующих
находится вращением вокруг горизонтально проецирующей оси, совпадающей с осью конуса. Концы
отрезков соединяем плавной кривой. Развертка боковой поверхности конуса построена.
114
Развертку боковой поверхности прямого кругового цилиндра заменяют разверткой боковой
поверхности правильной многоугольной призмы, вписанной в данный цилиндр.
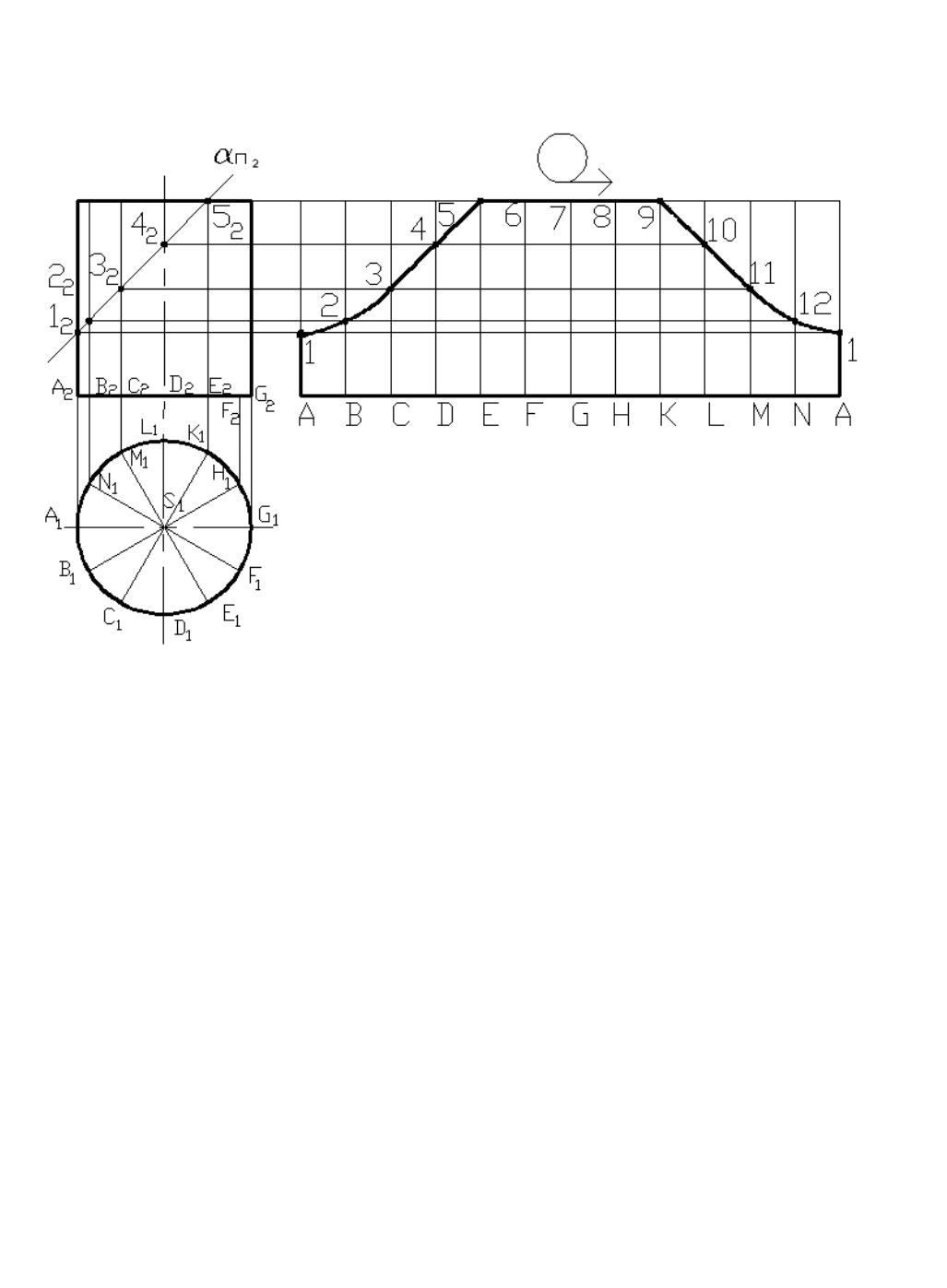
Пример 7.2
Построить развертку боковой поверхности прямого кругового цилиндра, усеченного плоскостью
α
.
Делим основание цилиндра на 12 равных частей и проводим через точки деления образующие
цилиндра.
На свободном поле чертежа проводим прямую, на которой откладываем последовательно от
произвольно точки A равные отрезки A – B, B – C,... Проводим через точки A, B,C,... перпендикуляры к
прямой и на них откладываем длины соответствующих образующих цилиндра.
Соединив концы образующих, расположенных на участке E – K прямой, а на остальных участках –
плавной кривой, получаем развертку боковой поверхности усеченного цилиндра.
Пример 7.3
Построить проекцию линии пересечения заданных поверхностей (рис. 7 3), используя способ
концентрических сфер. Построить развертку боковой поверхности конуса P
Применяя способ концентрических сфер, строим проекцию пинии пересечения заданных
концентрических поверхностей. Сфера минимального радиуса вписывается в больший конус.
Чтобы построить развертку конуса с линией пересечения заданных поверхностей, вынесем на
свободное поле чертежа две проекции конуса, развертку которого мы хотели получить.
Построим проекции S, и S,. вершины конуса S. Разделим окружность нижнего основания конуса на \2
равных частей. Проведем образующие конуса, проходящие через точки деления. Например, образующая
точки B имеет проекции B
1
S
1
и B
2
S
2
Точки линии пересечения поверхностей расположены на этих
образующих, это точки 1, 2, З…
Развертка конуса – это сектор окружности радиусом, равным длине образующей конуса. На дуге
окружности, проведенной из произвольной точки S. откладываем участки A – B, B – C, C – D и т.д., длины
которых равны длине соответствующих хорд A
1
B
1
, B
1
C
1
и т.д. окружности нижнего основания конуса. Через
точки A, B, C, D ... проводим образующие конуса, на которых откладываем длины образующих конуса.
Натуральную величину образующей A конуса определяем по фронтальной проекции конуса – отрезок
A
2
1
2
. Натуральную величину образующей B конуса находим, используя способ вращения вокруг оси,
перпендикулярной горизонтальной плоскости проекций П
1
и проходящей через вершину конуса S
Натуральная величина образующей – отрезок A
2
2*. Откладываем эту величину на развертке на образующей B
конуса. Натуральные величины остальных образующих находим аналогично.
Рис. 7.2
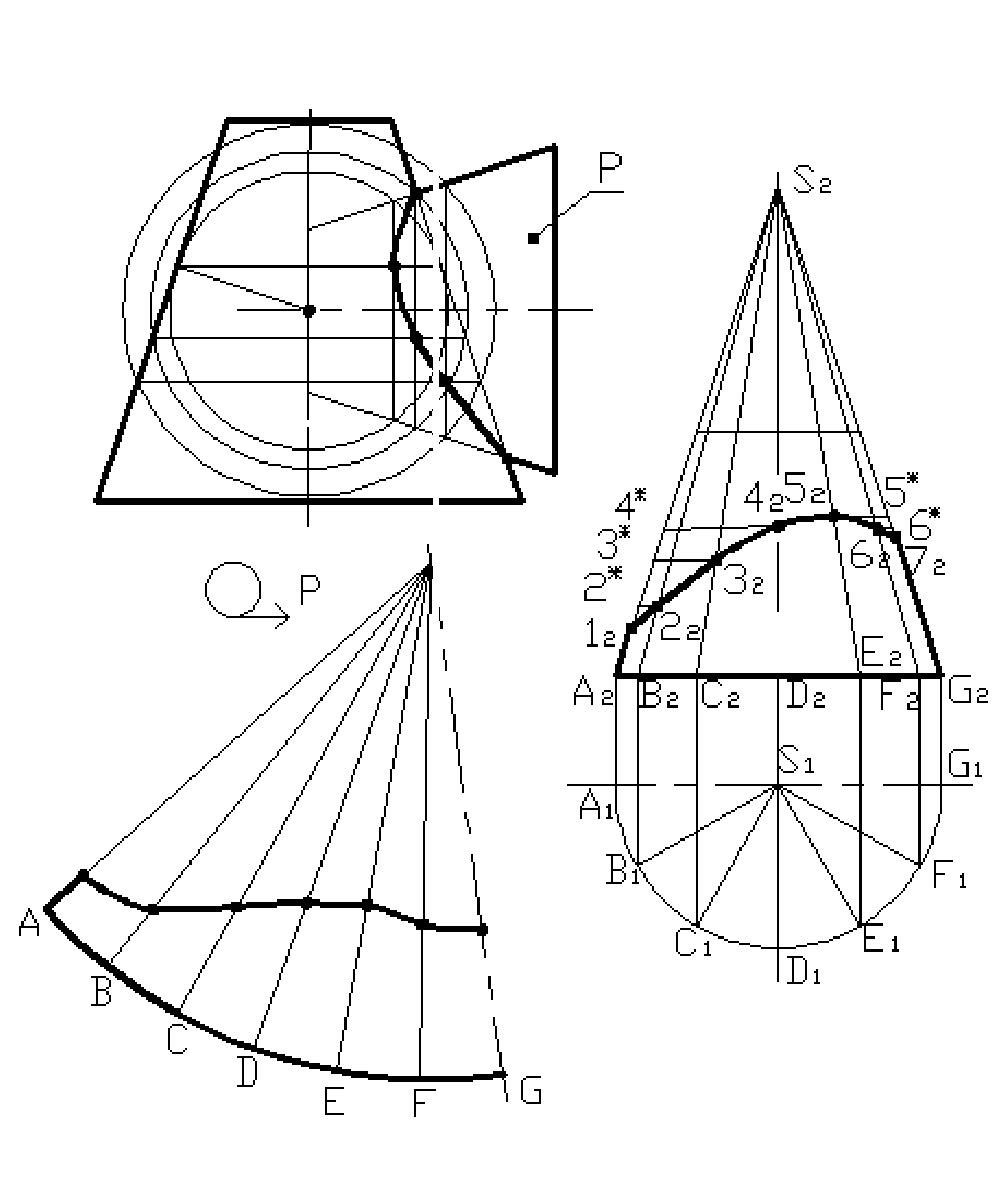
115
Рис. 7.3
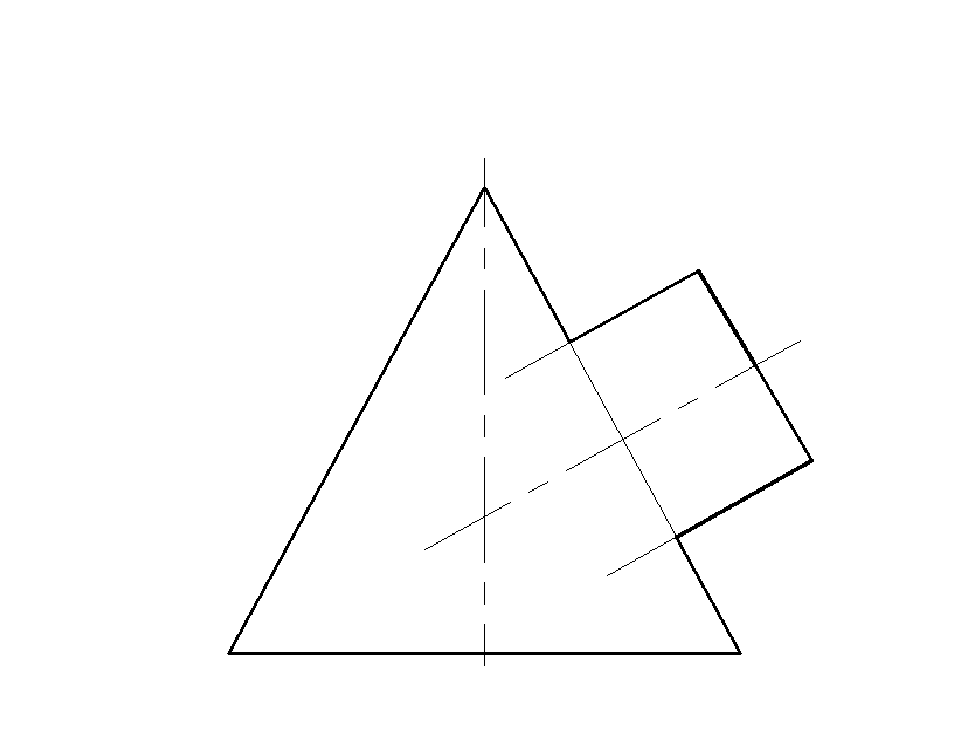
116
Задача 7.1
Построить проекцию линии пересечения конуса и цилиндра, используя способ концентрических сфер.
Построить развертку боковой поверхности цилиндра.
Рис 7.4
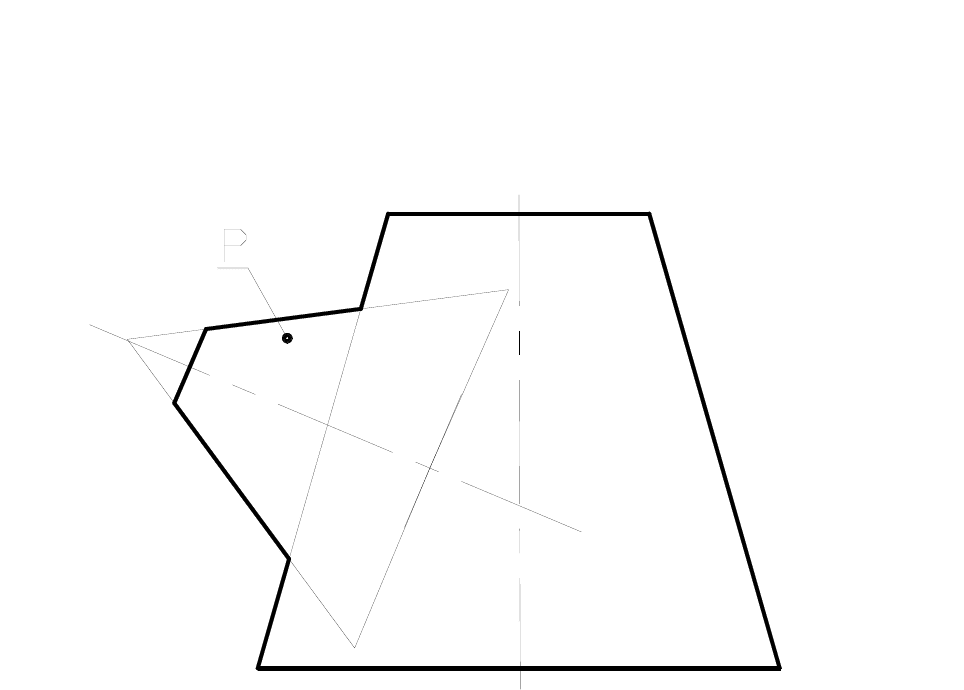
117
Задача 7.2
Построить проекцию линии пересечения конусов, используя способ концентрических сфер. Построить
развертку боковой поверхности конуса Р.
Рис 7.5
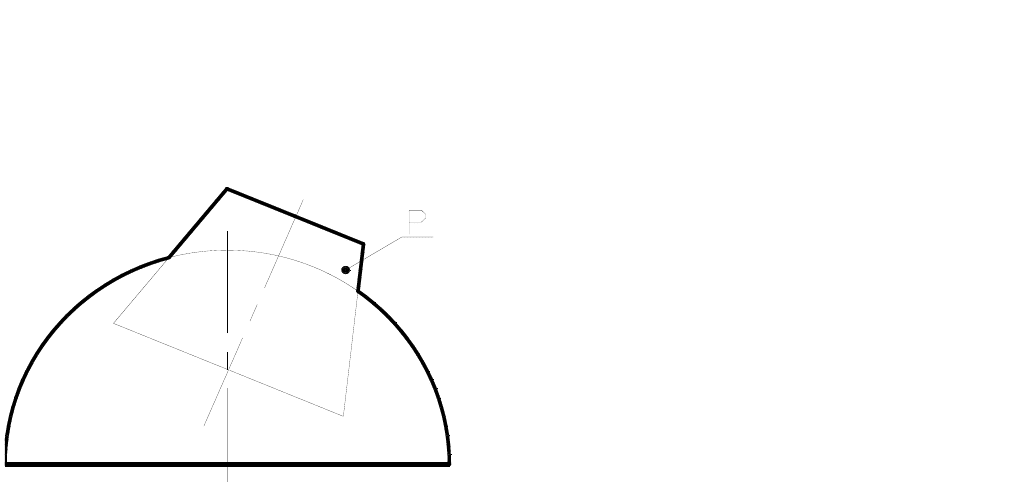
118
Задача 7.3
Построить проекцию линии пересечения полусферы и конуса, используя способ концентрических сфер.
Построить развертку боковой поверхности конуса Р.
Рис. 7.6

119
Для самостоятельной работы
