Пирс Б. Типы в языках программирования

Подождите немного. Документ загружается.

28.5. Неразрешимость Полной F

331

Определим теперь тип T следующим образом:

T X<:Top. ( Y<:X. Y)

Если с помощью алгоритмических правил наследования мы попробуем снизу вверх построить дерево

вывода для утверждения

<:T X

<: X

<:X

. X

мы получим бесконечную последовательность возрастающих подцелей:

<:T X

<: X

<:X

. X

<:T X

<:Top. ( X

<:X

. X

) <: X

<:X

. X

<:T, X

<:X

( X

<:X

. X

) <: X

<:T, X

<:X

<: X

<:X

. X

<:T, X

<:X

<: X

<:X

. X

и т. д.

Шаги переименования, требуемые, чтобы поддерживать корректность контекста, здесь производятся

без специального указания, и имена переменных выбираются так, чтобы лучше была видна схема беско-

нечного регресса. Основная хитрость состоит в «смене границ», которая происходит, например, между

второй и третьей строкой, где граница для X

на левой стороне, которая в строке 2 была равна Top, в

строке 3 становится равна X

. Поскольку в строке 2 вся левая сторона сама по себе является верхней

границей для X

, такая смена границ приводит к циклическому процессу, где на каждой итерации кон-

текст содержит все более и более длинные цепочки переменных. (Мы предупреждаем читателя, что не

стоит искать семантического смысла в этом примере; в частности, T представляет собой отрицание

только синтаксически.)

Хуже того, не только один определенный алгоритм зацикливается на некоторых входах, но можно

показать (Pierce 1994), что не существует алгоритма, корректного и полного относительно полной F

и завершающегося на всех входах. Доказательство этой теоремы слишком длинное для данной книги.

Однако, чтобы дать понятие о его духе, мы приведем еще один пример.

Определение 28.5.3 Положительные и отрицательные вхождения в типе T определяются следующим

образом. Сам T является положительным вхождением в T. Если T

является положительным

(соотв. отрицательным) вхождением, то T

является отрицательным (соотв. положительным)

вхождением, а T

является положительным (отрицательным) вхождением. Если X<:T

— по-

ложительное (соответственно, отрицательное) вхождение, то T

— отрицательное (соотв. поло-

жительное), а T

— положительное (отрицательное) вхождение. Положительные и отрицательные

вхождения в утверждение о наследовании Γ S <: T определяются так: тип S и границы типовых

переменных в Γ отрицательны, а тип T положителен.

Термины «положительный» и «отрицательный» происходят из логики. Согласно широко извест-

ному соответствию Карри-Ховарда между пропозициями и типами (§9.4), тип S T сопоставляется

логическому утверждению S T, которое, по определению логической импликации, эквивалентно

S T. Подутверждение S, очевидно, находится здесь в «отрицательной» позиции — а именно, внутри

нечетного количества отрицаний, — тогда и только тогда, когда вся импликация расположена внутри

четного количества отрицаний. Заметим, что положительное вхождение в T соответствует отрицатель-

ному вхождению в T.

Утверждение 28.5.4 Если X входит в S только положительно, а в T только отрицательно, то X<:U

S<:T тогда и только тогда, когда X U S <: X U T.

Доказательство: Упражнение .

Пусть теперь T будет следующий тип:

T X

<:Top. X

<:Top.

( Y

<:X

. Y

<:X

. Y

<:X

. X

)

rev. 104

332 28.5. Неразрешимость Полной F

Рассмотрим утверждение о наследовании

T <: X

<:T. X

<:P. X

<:Q.

( Y

<:Top. Y

<:Top.

( Z

<:Y

. Z

<:Y

. Z

<:Y

.U))

Это утверждение можно рассматривать как описание состояния некоторого компьютера. Переменные

и X

являются «регистрами» этой машины. Текущим состоянием этих регистров служат типы P и Q.

«Поток команд» машины содержится в третьей строке: первая команда закодирована в границах (Y

и Y

— обратите внимание на порядок) для переменных Z

и Z

, а непроясненный тип U представляет

оставшиеся команды в программе. Тип T, вложенные отрицания и границы переменных X

и Y

играют

приблизительно ту же роль, что и в более простом предыдущем примере: они позволяют нам «повернуть

рычаг» и вернуться к подцели, имеющей ту же форму, что и исходная цель. Один поворот рычага будет

соответствовать одному такту нашей машины.

В этом примере команда в начале потока команд кодирует собой инструкцию «обменять содержимое

регистров 1 и 2». Чтобы убедиться в этом, мы, с помощью двух установленных нами ранее утверждений,

проводим следующее вычисление. (Переменные P и Q, содержимое регистров, выделены, чтобы за ними

было проще следить.)

<: X

<:T. X

<: P . X

<: Q .

( Y

<:Top. Y

<:Top.

( Z

<:Y

. Z

<:Y

. Z

<:Y

.U))

титтк ( Y

<:T. Y

<: P . Y

<: Q . T)

<: ( Y

<:Top. Y

<:Top. по Утверждению 28.5.4

( Z

<:Y

. Z

<:Y

. Z

<:Y

.U))

титтк ( Y

<:Top. Y

<:Top.

( Z

<:Y

. Z

<:Y

. Z

<:Y

.U))

<: ( Y

<:T. Y

<: P . Y

<: Q . T) по Утверждению 28.5.2

титтк ( Z

<:T. Z

<: Q . Z

<: P .U)

<: T по Утверждению 28.5.4

титтк T

<: ( Z

<:T. Z

<: Q . Z

<: P .U) по Утверждению 28.5.2

Заметим, что в конце этого вывода не только поменялись местами значения P и Q, но в процессе была

использована команда, которая вызвала этот обмен, так что в начале потока «подлежащих исполнению»

команд оказался тип U. Если теперь в качестве значения U мы выберем тип, имеющий такой же вид,

как только что выполненная нами команда,

U ( Y

<:Top. Y

<:Top.

( Z

<:Y

. Z

<:Y

. Z

<:Y

.U’))

то мы проведем еще один обмен и вернем регистры к их исходному состоянию, прежде чем выполнить

U’. Или же мы можем выбрать другое значение U, вызывающее какое-либо другое поведение. Например,

если

U ( Y

<:Top. Y

<:Top.

( Z

<:Y

. Z

<:Y

. Z

<:Y

))

то на следующем такте исполнения машины текущее значение регистра Y

, т. е., Q, окажется в позиции

U — в сущности, будет произведен «косвенный переход» через регистр 1 к потоку команд, представля-

емому Q. Обобщив этот прием, можно закодировать условные конструкции и арифметику (операции

последователя, предшественника и проверку на ноль).

Взяв все это вместе, мы получаем доказательство неразрешимости путем сведения двухрегистровых

машин — простого варианта обыкновенных машин Тьюринга, где есть конечное устройство управления

и два счетчика, каждый из которых содержит натуральное число, — к утверждениям о наследовании.

Тогда и только тогда, когда. — прим. перев.

rev. 104

28.6. Объединения и пересечения 333

Теорема 28.5.5 Пирс, 1994 : Для каждой двухрегистровой машины M существует утверждение о

наследовании S M , такое, что S M выводимо в полной F

тогда и только тогда, когда вычисление

M завершается.

Таким образом, если бы мы могли решить, доказуемо ли произвольное утверждение о наследовании,

мы могли бы также решить, останавливается ли произвольная двухрегистровая машина. Поскольку

проблема останова для двухрегистровых машин неразрешима (см. Hopcroft and Ullman 1979), неразре-

шима и задача определения наследования для полной F

Следует еще раз подчеркнуть, что неразрешимость отношения наследования не означает, что по-

луалгоритм для наследования, разработанный в §28.4, некорректен либо неполон. Если утверждение

Γ S <: T доказуемо согласно декларативным правилам для наследования, алгоритм определенно

завершится и вернет значение истина. Если Γ S <: T не является выводимым согласно декларатив-

ным правилам, алгоритм либо не завершится, либо вернет значение ложь. Каждое данное утверждение

о наследовании может оказаться невыводимым одним из двух способов: либо оно порождает бесконеч-

ную последовательность подцелей (что означает отсутствие конечного вывода с данным заключением),

либо сводится к очевидному противоречию вроде Top <: S T. Алгоритм проверки наследования мо-

жет распознать один из этих случаев, но не другой.

Означает ли неразрешимость полной F

, что система практически бесполезна? Напротив, как пра-

вило, считают, что сама по себе неразрешимость F

не является таим уж серьезным недостатком.

Во-первых, было показано (Ghelli 1995), что, чтобы заставить процедуру проверки наследования за-

циклиться, нужно скормить ей цель с тремя достаточно экзотическими свойствами, и про каждое из

них трудно представить, что программист его породит случайно. Кроме того, существует немало по-

пулярных языков, для которых задача проверки типов в принципе либо чрезвычайно трудоемка — как

в ML или Haskell, как мы видели в §22.7, либо неразрешима, как для C++ или λProlog (Felty, Gunter,

Hannah, Miller, Nadathur and Scedrov 1988). На практике оказывается, что отсутствие объединений и

пересечений, о котором упоминается в следующем разделе (см. Упражнение 28.6.3) является намного

большим недостатком полной F

, чем неразрешимость.

Упражнение 28.5.6 : (1) Определите вариант полной F

без типа Top, но со связывания-

ми типов вида X<:T и вида X (т. е., как с ограниченной, так и с неограниченной квантификацией);

этот вариант называется полностью ограниченная квантификация. (2) Покажите, что отношение

наследования для этой системы разрешимо. (3) Дает ли такое ограничение удовлетворительное ре-

шение для проблем, обсуждаемых в этом разделе? В частности, будет ли оно работать в языках с

дополнительными конструкторами типов вроде чисел, записей, вариантов и т. п.?

28.6. Объединения и пересечения

В §16.3 мы убедились, что в языках с наследованием желательным свойством является наличие

объединения для всякой пары типов S и T — то есть, типа J, минимального среди всех общих надтипов

S и T. В этой главе мы показываем, что отношение наследования для ядерной F

, действительно, имеет

объединение для любой пары типов S и T, а также пересечение для любых S и T, имеющих хотя бы

один общий подтип, и даем алгоритмы для их вычисления. (Напротив, оба этих свойства отсутствуют

в полной F

; см. Упражнение 28.6.3.)

Мы пользуемся записью Γ S T J, означающей «J является объединением типов S и T в кон-

тексте Γ», а также Γ S T M, означающей «M является пересечением S и J в Γ». Алгоритмы для

вычисления этих отношений определяются одновременно на Рис. 28.5. Обратите внимание, что неко-

торые варианты в этих определениях пересекаются; чтобы определения работали как детерминистские

алгоритмы, мы объявляем, что всегда выбирается первый подходящий вариант.

Несложно убедиться, что и являются всюду определенными функциями, в смысле, что всегда

возвращает тип, а всегда либо возвращает тип, либо терпит неудачу. Для этого достаточно заметить,

что общий вес (см. Определение 28.3.4) типов S и T относительно Γ при рекурсивных вызовах всегда

уменьшается.

Теперь следует доказать, что по этим алгоритмам действительно вычисляются объединения и пе-

ресечения. Доказательство разбито на две части: Утверждение 28.6.1 показывает, что вычисленное

rev. 104

334 28.6. Объединения и пересечения

<: Top

Γ S T

T если Γ S <: T

S если Γ T <: S

J если S X

X<:U Γ

Γ U T J

J если T X

X<:U Γ

Γ S U J

если S S

T T

Γ S

X<:U

если S X<:U

T X<:U

Γ, X<:U

Top в остальных случаях

Γ S T

S если Γ S <: T

T если Γ T <: S

если S S

T T

Γ S

X<:U

если S X<:U

T X<:U

Γ, X<:U

неудача в остальных случаях

Рис. 28.5. Алгоритмы поиска объединений и пересечений для ядерной F

объединение является верхней гранью S и T, а пересечение (когда оно есть) является нижней гранью.

Затем Утверждение 28.6.2 показывает, что вычисленное объединение меньше любой верхней грани S и

T, а пересечение больше любой общей нижней грани (и существует всегда, когда у S и T имеется общая

нижняя грань).

Утверждение 28.6.1 1. Если Γ S T J, то Γ S <: J и Γ T <: J.

2. Если Γ S T M, то Γ M <: S и Γ M <: T.

Доказательство: Прямолинейная индукция по размеру вывода Γ S T J или Γ S T M

(т. е., по количеству рекурсивных вызовов, требуемых для вычисления J или M).

Утверждение 28.6.2 1. Если Γ S <: V и Γ T <: V, то Γ S T J для некоторого J, причем

Γ J <: V.

2. Если Γ L <: S и Γ L <: T, то Γ S T M для некоторого M, причем Γ L <: M.

Доказательство: Проще всего доказать обе части утверждения одновременной индукцией по ал-

горитмическим выводам утверждений Γ S <: V и Γ T <: V для части 1, и Γ M <: S и

Γ M <: T для части 2. (Благодаря Теореме 28.3.3 мы можем быть уверены, что алгоритмические

соответствия декларативным выводам всегда существуют.)

1. Если какой-либо из двух выводов является экземпляром правила SA-Top, то V Top, и требу-

емый результат, Γ J <: V, следует непосредственно.

Если вывод Γ T <: V является экземпляром правила SA-Refl-TVar, то T V. Но в таком

случае первый данный вывод дает нам Γ S <: V T, так что применим первый вариант

в определении объединения, и он дает нам Γ S T T, что удовлетворяет требованиям.

Подобным образом, если вывод Γ S <: V является экземпляром SA-Refl-TVar, то S V.

Но тогда второй данный вывод говорит, что Γ S T S, так что применим второй вари-

ант в определении объединения, и он дает нам Γ S T S, что опять же удовлетворяет

требованиям.

Если вывод Γ S <: V заканчивается экземпляром правила SA-Trans-TVar, то мы имеем

S X, причем X<:U Γ, и имеется подвывод Γ U T J. Третий вариант в определении

объединения дает нам Γ S T J, а из индуктивного предположения мы имеем Γ J <: V.

rev. 104

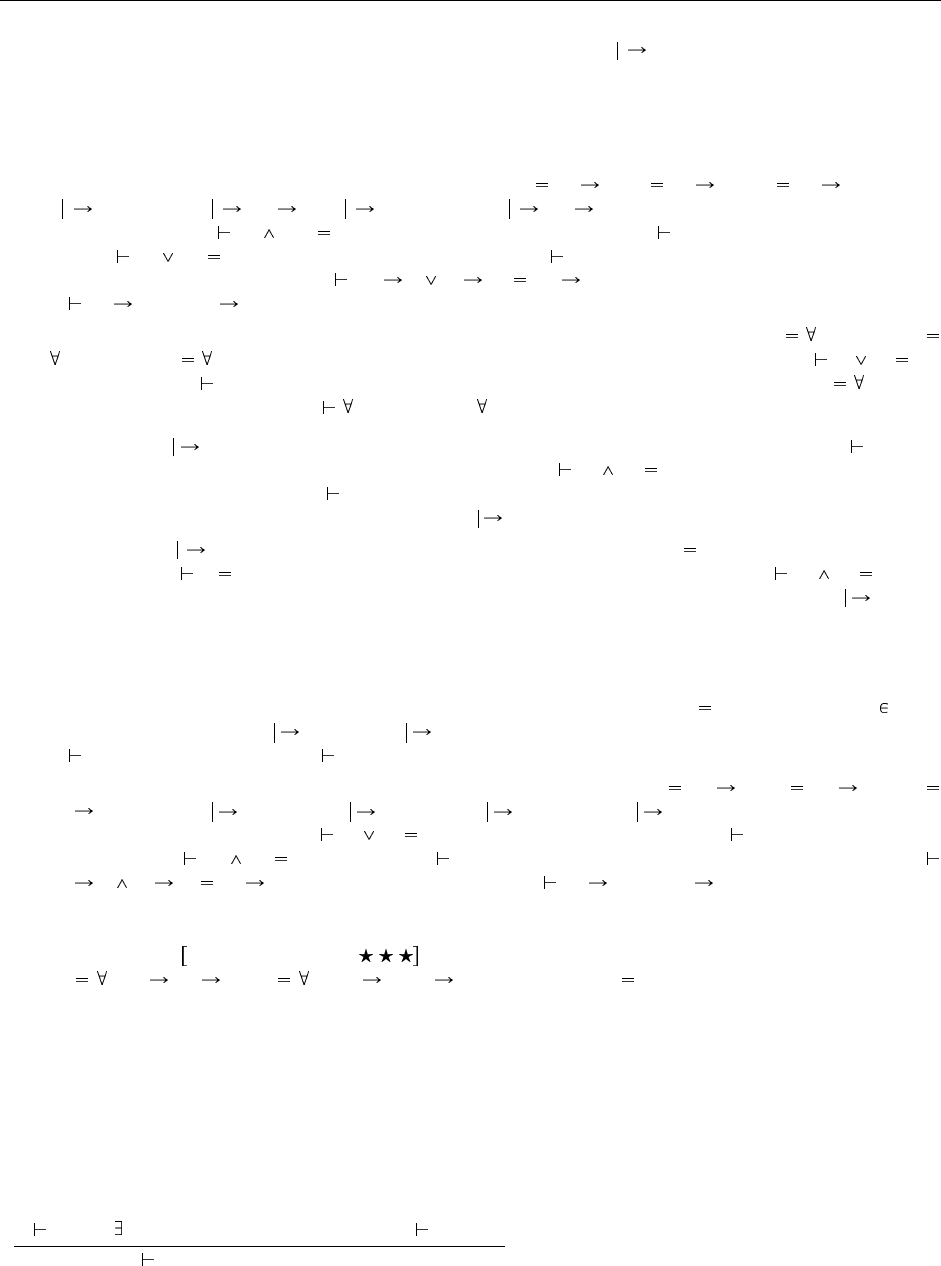
28.7. Ограниченные кванторы существования 335

Подобным образом мы рассуждаем и в том случае, когда Γ T <: V заканчивается на SA-

Trans-TVar.

Теперь несложно видеть, судя по форме алгоритмических правил наследования, что остаются

только варианты, когда оба данных вывода завершаются либо правилом SA-Arrow, либо SA-

All.

Если оба завершаются SA-Arrow, то мы имеем S S

, T T

и V V

, причем

Γ V

<: S

, Γ S

, Γ V

<: T

и Γ T

. Согласно части (2) предположе-

ния индукции, Γ S

для некоторого M

, причем Γ V

<: M

, а согласно части

(1), Γ S

для некоторого J

, причем Γ J

<: M

. Пятый вариант в определе-

нии объединений дает нам Γ S

, а по правилу S-Arrow мы имеем

Γ M

<: V

Наконец, если оба данных нам вывода заанчиваются на SA-All, то мы имеем S X<:U

, T

X<:U

и V X<:U

. Согласно части (1) предположения индукции, Γ, X<:U

причем Γ, X<:U

<: V

. Шестой вариант в определении объединений дает нам J X<U

а по правилу S-All имеем Γ X<:U

<: X<:U

2. Если вывод Γ L <: T заканчивается на SA-Top, то тип T равен Top, так что Γ S <: T,

и, по первому варианту в определении пересечения, Γ S T S. Однако из второго данного

нам вывода мы знам, что Γ L <: S, так что требуемое утверждение доказано. Подобным

образом рассуждаем и в случае, когда вывод Γ L <: S заканчивается на SA-Top.

Если вывод Γ L <: S заканчивается на SA-Refl-TVar, то L S, и второй данный нам

вывод дает Γ L S <: T, откуда по определению пересечения мы имеем Γ S T S, так

что доказательство закончено. Подобным образом рассуждем также, когда вывод Γ L <: T

заканчивается на SA-Refl-TVar.

Остаются только варианты, когда оба данных нам вывода заканчиваются на SA-Trans-TVar,

SA-Arrow или SA-All.

Если оба вывода заканчиваются на SA-Trans-TVar, то имеем L X, причем X<:U Γ, и

имется два подвывода Γ U <: S и Γ U <: T. Согласно части (2) предположения индукции,

Γ U <: M, откуда имеем Γ L <: M по правилу S-TVar и транзитивности.

Если оба вывода заканчиваются на SA-Arrow, то мы имеем S S

, T T

и L

, причем Γ S

<: L

, Γ L

<: S

, Γ T

<: L

и Γ L

<: T

. Согласно части (1)

предположения индукции, Γ S

для некоторого J

, причем Γ J

<: L

, а согласно

части (2), Γ S

, причем Γ L

<: M

. Определение пересечений дает нам Γ

, а по правилу S-Arrow, Γ L

<: J

Подобным образом ведется доказательство и в варианте с правилом SA-All.

Упражнение 28.6.3 Рекомендуется, : Рассмотрим пару типов (предложенных Гелли, Ghelli

1990) S X<:Y Z.Y Z и T X<:Y’ Z’.Y’ Z’ и контекст Γ Y<:Top, Z<:Top, Y’<:Y, Z’<:Z. (1)

Сколько в полной F

существует типов, являющихся подтипами как S, так и T в контексте Γ? (2)

Покажите, что в полной F

типы S и T не имеют пересечения в контексте Γ. (3) Найдите пару

типов, которые в полной F

не имеют объединения в контексте Γ.

28.7. Ограниченные кванторы существования

Чтобы расширить алгоритм ядерной F

на язык с кванторами существования, нужно справиться с

одной дополнительной трудностью. Напомним декларативное правило удаления для экзистенциальных

типов:

Γ t

: { X<:T

} Γ, X<:T

, x:T

: T

Γ let {X,x}=t

in t

: T

(T-Unpack)

В §24.1 мы обратили внимание, что типовая переменная X присутствует в контексте, где во вто-

рой предпосылке вычисляется тип терма t, но отсутствует в контексте заключения правила. Это

означает, что тип T

не должен содержать X в качестве свободной переменной, поскольку всякое такое

rev. 104

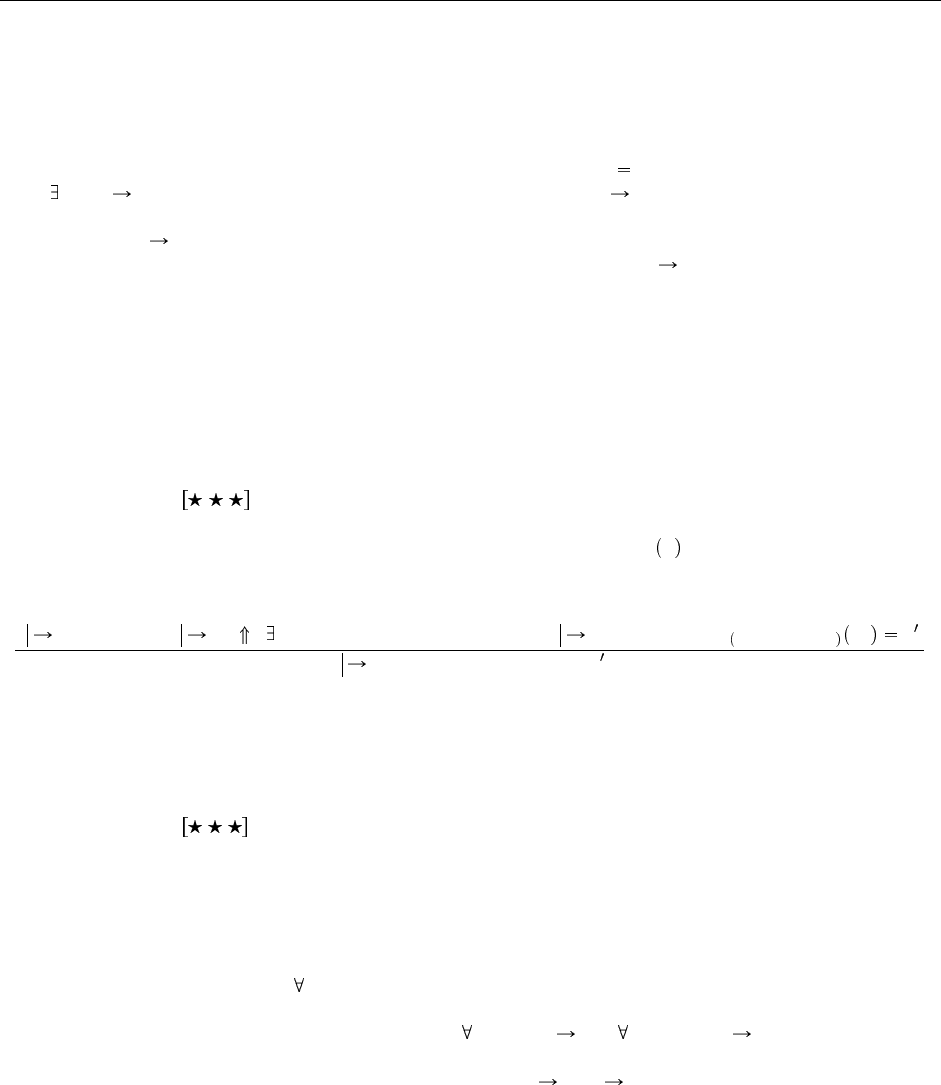
336 28.8. Ограниченная квантификация и тип BOT

вхождение в заключении окажется вне области видимости. Более подробно этот вопрос обсуждался в

§25.5, где мы указали, что изменение контекста от предпосылки к заключению соответствует отрица-

тельному сдвигу индексов переменных в T

, когда мы представляем термы в безымянном формате де

Брауна; этот сдвиг будет неудачен, если X содержится в T

как свободная.

Как это обстоятельство влияет на алгоритм минимальной типизации для языка с экзистенциаль-

ными типами? В частности, что нам делать с выражением вроде t let {X,x} = p in x, где p имеет

тип { X,Nat X}? Наиболее естественным типом тела x будет Nat X, упоминающий связанную пере-

менную X. Однако согласно декларативному отношению типизации (с правилом включения), x имеет

также типы Nat Top и Top. Поскольку ни в одном из этих типов X не встречается, терму t в целом

можно в декларативной системе без всякой ошибки присвоить типы Nat Top и Top. В общем случае, в

выражении распаковки всегда можно поднять тело до типа, где не содержится свободной переменной X,

а затем применить T-Unpack. Так что, если мы хотим, чтобы наш алгоритм минимальной типизации

был полон, при работе с выражением распаковки, где минимальный тип тела T

содержит свободное

вхождение связанной переменной X, он не должен просто объявлять об ошибке. Вместо этого следует

поднять T

до некоторого типа, где X не упоминается. Основное утверждение, которое требуется, чтобы

такая идея сработала, состоит в том, что множество надтипов данного типа, не содержащих X, всегда

имеет минимальный элемент. Это показывает следующее упражнение (решение которого было найдено

Гелли и Пирсом, Ghelli and Pierce 1998).

Упражнение 28.7.1 : Постройте алгоритм, вычисляющий в ядерной F

с ограниченными эк-

зистенциальными типами минимальный надтип данного типа T, не содержащий переменной X, по

отношению к данному контексту Γ. Такой надтип обозначается R

X,Γ

T .

Теперь алгоритмическое правило типизации для удаления кванторов существования можно запи-

сать так:

Γ t

: T

Γ T

{ X<:T

} Γ, X<:T

, x:T

: T

X, Γ,X<:T

,x:T

Γ let {X,x}=t

in t

: T

(T-Unpack)

Как и следовало ожидать, в полной F

с ограниченными кванторами существования ситуация

сложнее. Гелли и Пирс (Ghelli and Pierce 1998) приводят пример типа T, контекста Γ и переменной

X, таких, что множество надтипов T, не содержащих X, не имеет минимального элемента в контексте

Γ. Отсюда немедленно следует, что отношение типизации в такой системе не обладает минимальными

типами.

Упражнение 28.7.2 : Покажите, что отношение типизации для варианта полной F

, имею-

щего только кванторы существования (т. е., без кванторов общности) также неразрешимо.

28.8. Ограниченная квантификация и тип Bot

Добавление минимального типа Bot несколько усложняет метатеоретические свойства F

. Это про-

исходит оттого, что в типе вида X<:Bot.T внутри T переменная X является, на самом деле, синонимом

для Bot, поскольку по предположению X — подтип Bot, а Bot, по правилу S-Bot, — подтип X. В свою

очередь, отсюда следует, что пары типов вроде X<:Bot.X X и X<:Bot.Bot Bot эквивалентны в

отношении наследования, хотя синтаксически они различаются. Более того, если контекст содержит

предположения X<:Bot и Y<:Bot, то эквивалентны типы X Y и Y X, при том, что ни в одном из них

Bot явно не упоминается. Несмотря на все это, даже при наличии Bot все основные свойства F

все

равно сохраняются. Детали можно найти в (Pierce 1997a).

rev. 104

Часть VI

Системы высших порядков

337

Глава 29

Операторы над типами и виды

В предыдущих главах мы часто, чтобы облегчить чтение примеров, употребляли сокращения вроде

CBool = X. X -> X -> X

Pair Y Z = X . (Y ->Z -> X ) -> X

и писали, скажем, λx:Pair Nat Bool. x, вместо более громоздкого λx:(Nat->Bool->X)->X. x.

Запись CBool — просто сокращение; когда она встречается в примере, следует просто заменить её на

правую часть определения. Запись Pair, напротив, параметризованное сокращение; когда мы видим

Pair S T, требуется в его определении заменить параметры Y и Z на реальные типы S и T. Другими сло-

вами, параметрические сокращения вроде Pair дают нам неформальный способ определения функций

на уровне выражений типа.

Мы уже использовали выражения на уровне типа вроде Array T или Ref T. В них используются

конструкторы типов Array и Ref. Несмотря на то, что эти конструкторы не определены програм-

мистом, а встроены в язык, они также являются разновидностью функций на уровне типов. Можно

рассматривать, скажем, Ref, как функцию, которая для каждого типа T выдает тип ссылочных ячеек,

содержащих элементы T.

В этой и последующих двух главах нашей задачей будет более формальное рассмотрение таких

функций на уровне типа, совместно называемых операторами над типами. В этой главе мы вводим

основные механизмы абстракции и применения на уровне типов, точное определение того, когда следует

считать два выражения типа эквивалентными, а также отношение корректности построения, назвае-

мое отношением видообразования, не позволяющее нам писать бессмысленные типовые выражения.

Глава 30 идет еще на шаг дальше; там операторы над типами рассматриваются как полноправные эле-

менты языка — т. е., как сущности, которые можно передавать аргументами в функции. В этой главе

вводится известная Система F

, обобщающая квантификацию по типам из Системы F (Глава 23) до

квантификации высшего порядка по операторам типов. В Главе 31 рассматривается сочетание опера-

торов над типами, квантификации высшего порядка и наследования.

29.1. Неформальное введение

Первое, что нам требуется при изучении функций на уровне типов — нотация для абстракции и при-

менения типов. Как правило, для этого используется та же запись, то и для абстракции и применения

на уровне термов, то есть, абстракция обозначается через λ, а применение через соположение.

Напри-

В этой главе вводится простое типизированной лямбда-исчисление с операторами типов, λ

(Рис. 29.1). В приме-

рах, кроме того, используются числа и булевские значения (8.2), а также универсальные типы (23.1). Соответствующий

интерпретатор на OCaml называется fullomega.

У подобной нотационной экономии есть тот недостаток, что терминология для выражений различного вида ино-

гда оказывается довольно запутанной. Например, выражение «абстракция типа» может теперь обозначать абстракцию,

ожидающую тип в качестве аргумента (т. е., терм вида λX.t), а может абстракцию на уровне типов (т. е., выражение

типа вроде λX.{a:X}). В контекстах, где возможно и то, и другое, обычно предпочитают в первом смысле использовать

339

340 29.1. Неформальное введение

мер, λX.{a:X,b:X} обозначает функцию, которая, принимая тип T, выдает тип записей {a:T,b:T}.

Применение этой функции к типу Bool записывается (λX.{a:X,b:X}) Bool.

Подобно обыкновенным функциям, типовые функции от нескольких аргументов получаются из од-

ноаргументных через карринг. Например, выражение типа λY. λZ. X. (Y Z X) X представляет

двухместную функцию — или, строго говоря, одноместную функцию, которая, будучи применена к типу

S, даст другую одноместную функцию, которая при применении к типу T даст тип X.(S T X) X.

Мы будем продолжать пользоваться неформальными сокращениями для длинных выражений типа,

включая операторы над типами. Например, в оставшейся части этой главы мы будем считать, что

имеется сокращение

Pair = λY . λZ . X . (Y ->Z ->X ) -> X ;

Так что когда мы в примерах пишем Pair S T, имеется в виду

(λY . λZ . X . (Y ->Z ->X ) -> X ) S T .

Другими словами, вместо неформального соглашения о параметрических сокращениях, которым мы

пользовались до сих пор, теперь у нас будет более простое неформальное соглашение, что все простые

сокращения заменяются на свои правые части, дополненное формальными механизмами определения и

конкретизации операторов над типами. Операции определения и расширения сокращений также можно

формально определить — т. е„ их можно сделать операциями объектного языка, а не соглашениями

метаязыка, — но этим мы здесь заниматься не будем. Заинтересованные читатели могут обратитья к

литературе по системам типов с определениями или одноэлементными видами; см. труды Севери и

Полла (Severi and Poll 1994), Стоуна и Харпера (Stone and Harper 2000), Крэри (Crary 2000), а также

приведенные там ссылки.

Абстракция и применение на уровне типов позволяет нам записывать один и тот же тип несколькими

различными способами. Например, если Id служит сокращением для оператора над типами λX.X, то

выражения

Nat Bool Nat Id Bool Id Nat Id Bool

Id Nat Bool Id (Nat Bool) Id (Id (Id Nat Bool))

являются различными именами одного и того же функционального типа. Чтобы сделать это интуи-

тивное понятие формально точным, мы вводим отношение эквивалентности определений для типов.

Эквивалентность определений записывается как S T. Самое важное уравнение в определении этого

отношения

(λX::K

. T

) T

X T

(Q-AppAbs)

говорит, что абстрация на уровне типов, примененная к аргументу, эквивалентна телу этой абстракции,

где вместо формального параметра подставлен аргумент. Эквивалентность определений используется

при проверке типов в новом правиле

Γ t : S S T

Γ t : T

(T-Eq)

формально выражающем интуицию, что когда два типа эквивалентны, элементы одного из них явля-

ются также элементами другого.

Еще одна новая возможность, проистекающая из наличия механизмов абстракции и применения ти-

пов — способность писать бессмысленные типовые выражения. Например, применение одного обыкно-

венного типа к другому, скажем, в типовом выражении (Bool Nat), столь же абсурдно, кк применение

true к 6 на уровне термов. Чтобы избежать такой бессмыслицы, мы вводим систему видов, согласно

которой типы классифицируются по своим аргументам, так же как функциональные типы указывают

нам, что за аргументы ожидаются для термов.

Виды строятся на основе одного элементарного вида, изображаемого в виде * и читаемого «тип», и

одного двуместного конструктора . Видами являются, например,

выражение «полиморфная функция», а во втором «абстракция на уровне типов» или «операторная абстракция».

rev. 104