Пирс Б. Типы в языках программирования
Подождите немного. Документ загружается.

Глава 26
Ограниченная квантификация
Многие интересные проблемы в языках программирования проявляются при взаимодействии
свойств и конструкций, которые, взятые сами по себе, относительно просты. В этой главе мы вводим
ограниченную квантификацию, возникающую при сочетании полиморфизма и наследования. При этом
существенно увеличивается как выразительная сила системы, так и ее метатеоретическая сложность.
Исчисление, с которым мы будем работать, называется F
<:
. Оно играло важную роль в исследованиях
по языкам программирования с тех пор, как было открыто в середине 80-х; в частности, в работах по
основаниям объектно-ориентированного программирования.
26.1. Мотивация
Простейший способ совместить наследование и полиморфизм состоит в том, чтобы считать их орто-
гональными характеристиками языка — т. е., рассмотреть систему, по существу, являющуюся объеди-
нением систем из Глав 15 и 23. Такое сочетание не вызывает теоретических трудностей и может быть
полезно по тем же причинам, по которым наследование и полиморфизм полезны отдельно друг от дру-
га. Однако как только мы получаем обе характеристики в одном языке, возникает соблазн сочетать их
более интересным способом. В качестве иллюстрации рассмотрим простой пример — в дальнейшем мы
встретим другие примеры в §26.3, а также более развернутые программы в Главах 27 и 32.
Предположим, f является функцией тождества на записях с числовым полем a:
f = λx :{ a : Nat }. x ;
f : { a: Nat } -> {a: Nat }
Если ra — запись, имеющая такое поле,
ra = { a =0};
то мы можем применить f к ra — в любой из рассмотренных нами ранее систем, — и получить запись
того же типа.
f ra ;
{a =0} : {a : Nat }
Подобным образом, если мы определим запись rab большего размера с двумя полями, a и b,
rab = { a =0 , b= true };
то мы также можем применить f к rab, применяя правило включения (T-Sub, Рис. 15.1) и повышая
тип rab до {a:Nat}, чтобы она соответствовала типу, ожидаемому функцией f.
На протяжении большей части этой главы исследуется чистая Система F
<:
(Рис. 26.1). В примерах используются
также записи (11.7) и числа (8.2). Соответствующие интерпретаторы на OCaml называются fullsub и fullfomsub. (Для
большинства примеров достаточно fullsub; для примеров, включающих сокращения типов с параметрами, вроде Pair,
требуется fullfomsub.)
301
302 26.2. Определения
f rab ;
{a =0 , b = true } : {a: Nat }
Однако тип результата при таком применении имеет только поле a. Следовательно, терм вроде (f
rab).b окажется неправильно типизированным. Другими словами, пропустив rab через функцию тож-
дества, мы потеряли право обращаться к ее полю b!
Используя полиморфизм Системы F, мы можем записать f иначе:
fpoly = λX . λx:X. x ;
fpoly : X. X -> X
Применение функции fpoly к rab (с соответствующим аргументом-типом) дает желаемый результат:
fpoly [{ a:Nat , b : Bool }] rab ;
{a =0 , b = true } : {a: Nat , b: Bool }
Однако превратив тип x в переменную, мы потеряли некоторую информацию, которая могла быть нам
полезна. Допустим, например, что нам хочется написать другую версию f, возвращающую пару из
исходного аргумента и последователя его поля a:
f2 = λx :{ a: Nat }. { orig =x , asucc = succ (x. a )};
f2 : { a : Nat } -> { orig :{ a: Nat }, asucc : Nat }
С помощью наследования мы по-прежнему можем применить f2 как к ra, так и к rab, во втором случае
теряя поле b.
f2 ra ;
{ orig ={ a=0} , asucc =1} : { orig :{ a: Nat }, asucc : Nat }
f2 rab ;
{ orig ={ a=0 ,b = true }, asucc =1} : { orig :{ a: Nat }, asucc : Nat }
Но теперь полиморфизм не предлагает нам никакого решения. Если мы, как и раньше, заменим тип
x переменной X, мы потеряем ограничение, что x должен быть записью с полем a, а это ограничение
нужно, чтобы вычислить поле asucc результата.
f2 poly = λX. λx: X . { orig =x , asucc = succ (x . a )};
Ошибка: Ожидается тип записей
Информация об операционном поведении f2, которую мы хотели бы выразить в ее типе, состоит в
том, что f2 принимает аргумент любого типа записей R, где есть числовое поле a, и возвращает как
результат запись, содержащую поле типа R и поле типа Nat. С помощью отношения наследования мы
можем выразить это кратко: f2 принимает аргумент любого подтипа R типа {a:Nat} и возвращает
запись с полем типа R и полем типа Nat. Эту интуицию можно формализовать, введя ограничение на
наследование для связанной переменной X в f2poly.
f2 poly = λX <:{ a: Nat }. λx:X . { orig =x , asucc = succ (x . a )};
f2 poly : X <:{ a: Nat }. X -> { orig :X , asucc : Nat }
Эта так называемая ограниченная квантификация является основной характеристикой Системы F
<:
.
26.2. Определения
С формальной точки зрения, Система F
<:
получается сочетанием типов и термов Системы F из
Главы 23 с отношением наследования из Главы 15, и добавлением к кванторам общности ограничений
на наследование. Подобным же образом можно определить и ограниченные кванторы существования,
как мы увидим в §26.5.
rev. 104
26.2. Определения 303
Существует, на самом деле, два различных разумных способа определить отношение наследования
в F
<:
. Они отличаются формулировкой правила для сравнения ограниченных кванторов (S-All): есть
версия, которая легче описывается формально, но менее гибкая, так называемое ядерное правило, и
более выразительное, но вызывающее технические трудности полное правило наследования. В следую-
щих разделах мы подробно описываем обе версии, сначала вводя ядерный вариант, а затем, в §26.2.5,
полный вариант. Когда нам нужно точно указывать, о каком варианте идет речь, мы будем называть
версии исчисления соответственно ядерная F
<:
и полная F
<:
. Имя F
<:
без прилагательных относится к
обеим системам.
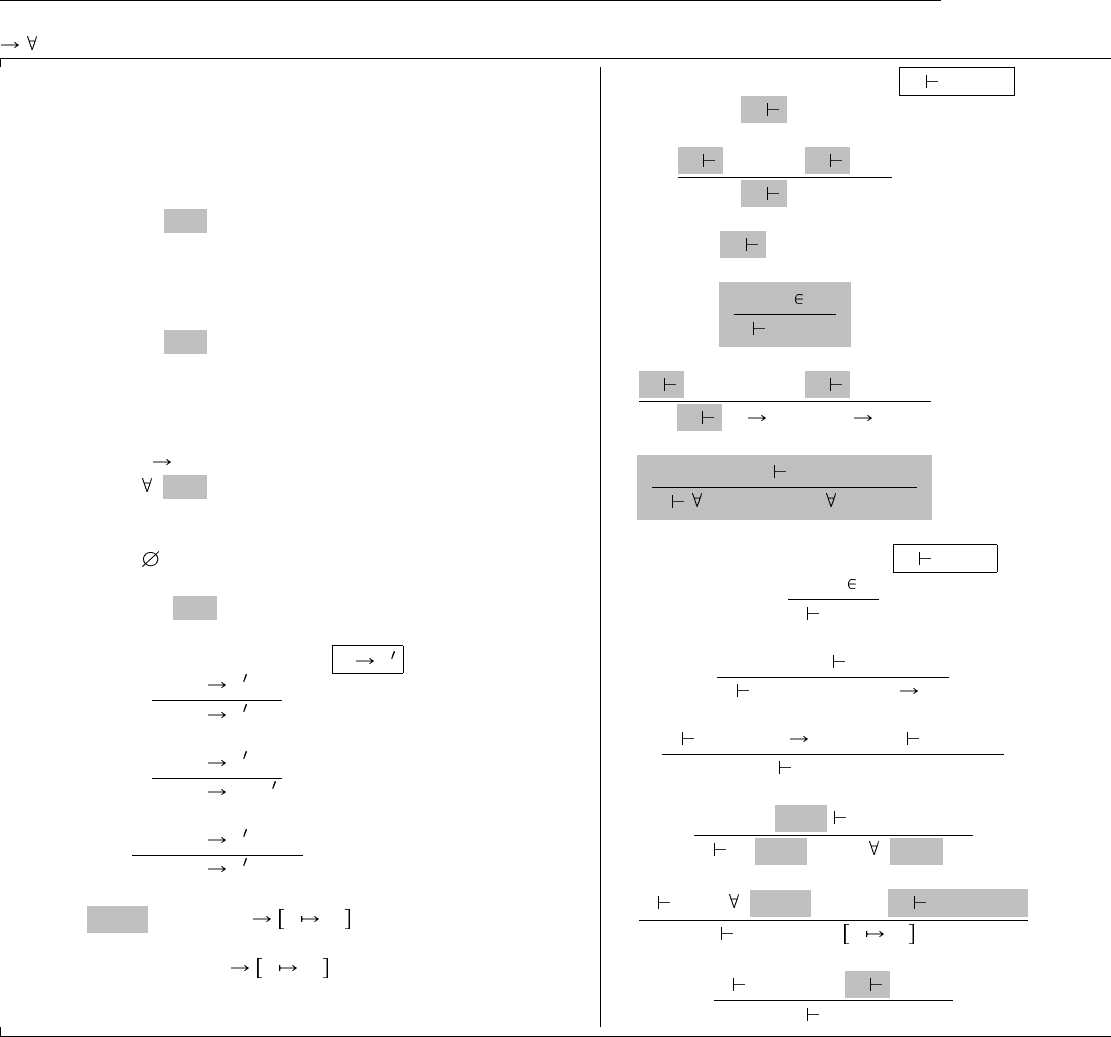
На Рис. 26.1 приведено полное определение ядерной F
<:
; отличия от предыдущих систем выделены.
26.2.1. Ограниченная и неограниченная квантификация
Одна деталь, которая немедленно видна при взгляде на это определение — синтаксис F
<:
разрешает
только ограниченную квантификацию: обычная, неограниченная квантификация Системы F исчезла.
Причина состоит в том, что она не нужна: ограниченный квантор, чье ограничение равно Top, охватыва-
ет все подтипы Top — а значит, все типы вообще. Таким образом, мы восстанавливаем неограниченную
квантификацию в виде скоращения:
X.T
def
X<:Top.T
Это сокращение часто используется в тексте.
26.2.2. Области видимости
Важная техническая подробность, неочевидная из Рис. 26.1, касается областей видимости типовых
переменных. Очевидно, что всякий раз, когда мы упоминаем утверждение типизации вида Γ t : T,
мы хотим, чтобы свободные типовые переменные, встречающиеся в t и T, были определены в Γ. Однако
что происходит со свободными типовыми переменными, входящими в типы внутри Γ? В частности,
какие из следующих контекстов должны считаться правильно образованными с точки зрения областей
видимости?
Γ
1
X<:Top, y:X Nat
Γ
2
y:X Nat, X<:Top
Γ
3
X<:{a:Nat,b:X}
Γ
4
X<:{a:Nat,b:Y}, Y<:{c:Bool,d:X}
Γ
1
, несомненно, образован правильно: он вводит типовую переемнную X, а затем термовую переменную
y, в чьем типе упоминается X. Терм, который может привести к такому контексту в процессе проверки
типов, будет иметь вид λX<:Top. λy:X Nat. t. Ясно, что переменная X в типе y связана вышележащей
λ. С другой стороны, по тем же причинам Γ
2
должен быть неверным, поскольку в термах, которые
могли бы привести к такому контексту — скажем, λy:X Nat. λX<:Top. t, — неясно, какова ожидаемая
область видимости X.
Γ
3
— более интересный случай. Можно доказывать, что он правилен и возникает в термах вроде
λX<:{a:Nat,b:X}. t, где второе вхождение X связанное. Для этого только требуется считать областью
видимости X участок кода, включающий его собственную верхнюю границу (а также, как обычно,
все, что стоит справа от связывания). Разновидность ограниченной квантификации, принимающая это
уточнение, называется F-ограниченная квантификация (Canning, Cook, Hill, Olthoff and Mitchell 1989b).
F-ограниченная квантификация часто упоминается в дискуссиях о типах в объектно-ориентированном
программировании, и использовалась в проекте языка GJ (Bracha, Odersky, Stoutamire and Wadler
1998). Однако теория этого вычисления несколько сложнее, чем в обыкновенной F
<:
(Ghelli 1997; Baldan,
Ghelli and Rafaet`a 1999), и становится по-настоящему интересной только когда в систему включаются
рекурсивные типы (ни один нерекурсивный тип X не может удовлетворять условию X<:{a:Nat,b:X}).
Контексты еще более общего вида, вроде Γ
4
, где позволяется взаимная рекурсия между типовы-
ми переменными через их верхние границы, тоже существуют. В таких исчислениях каждому новому
связыванию переменной, как правило, разрешается вводить произвольное множество неравенств, на-
лагающих ограничения как на новую переменную, так и на уже существующие.
В этой книге мы больше не будем рассматривать F-связанную квантификацию, и будем считать, что
Γ
2
, Γ
3
и Γ
4
все образованы неверно. Выражаясь более формально, мы будем требовать, чтобы каждый
rev. 104
304 26.2. Определения
<: Top Основана на Системе F (23.1) и простом наследовании (15.1)
Синтаксис
t ::= термы:
x переменная
λx:T.t абстракция
t t применение
λX <:T .t абстракция типа
t [T] применение типа
v ::= значения:
λx:T.t значение-абстракция
λX <:T .t значение-абстракция типа
T ::= типы:
X типовая переменная
Top максимальный тип
T T тип функций
X <:T .T универсальный тип
Γ ::= контексты:
пустой контекст
Γ, x:T связывание термовой переменной
Γ, X <:T связывание типовой переменной
Вычисление t t
t
1
t
1
t
1
t
2
t
1
t
2
(E-App1)
t
2
t
2
v
1
t
2
v
1
t
2
(E-App2)
t
1
t
1
t
1
[T
2
] t
1
[T
2
]
(E-TApp)
(λX <:T
11
.t
12
) [T
2
] X T
2
t
12
(T-TappTabs)
(λx:T
11
.t
12
) v
2
x v
2
t
12
(E-AppAbs)
Наследование Γ S <: T
Γ S<:S (S-Refl)
Γ S<:U Γ U<:T
Γ S<:T
(S-Trans)
Γ S <: Top (S-Top)
X<:T Γ
Γ X <: T
(S-TVar)
Γ T
1
<: S
1
Γ S
2
<: T
2
Γ S
1
S
2
<: T
1
T
2
(S-Arrow)
Γ, X<:U
1
S
2
<: T
2
Γ X<:U
1
.S
2
<: X<:U
1
.T
2
(S-All)
Типизация Γ t : T
x : T Γ
Γ x : T
(T-Var)
Γ, x:T
1
t
2
:T
2
Γ λx:T
1
.t
2
: T
1
T
2
(T-Abs)
Γ t
1
: T
11
T
12
Γ t
2
: T
11
Γ t
1
t
2
: T
12
(T-App)
Γ, X <:T
1
t
2
: T
2
Γ λX <:T
1
.t
2
: X <:T
1
.T
2
(T-TAbs)
Γ t
1
: X <:T
11
.T
12
Γ T
2
<: T
11
Γ t
1
[T
2
] : X T
2
X.T
12
(T-TApp)
Γ t : S Γ S <: T
Γ t : T
(T-Sub)
Рис. 26.1. Ограниченная квантификация (ядерная F
<:
)
раз, как в каком-либо контексте упоминается тип T, все свободные переменные T были связаны в отрезке
контекста слева от места, где встречается T.
26.2.3. Наследование
Каждая типовая переменная в F
<:
связана с некоторым ограничением (точно так же, как каждая
обыкновенная термовая переменная связана с некоторым типом), и во время проверки наследования
и типов мы должны отслеживать эти ограничения. Для этого мы изменяем связывания типов в кон-
текстах, и для каждой типовой переменной храним верхнюю границу. Во время проверки наследования
rev. 104
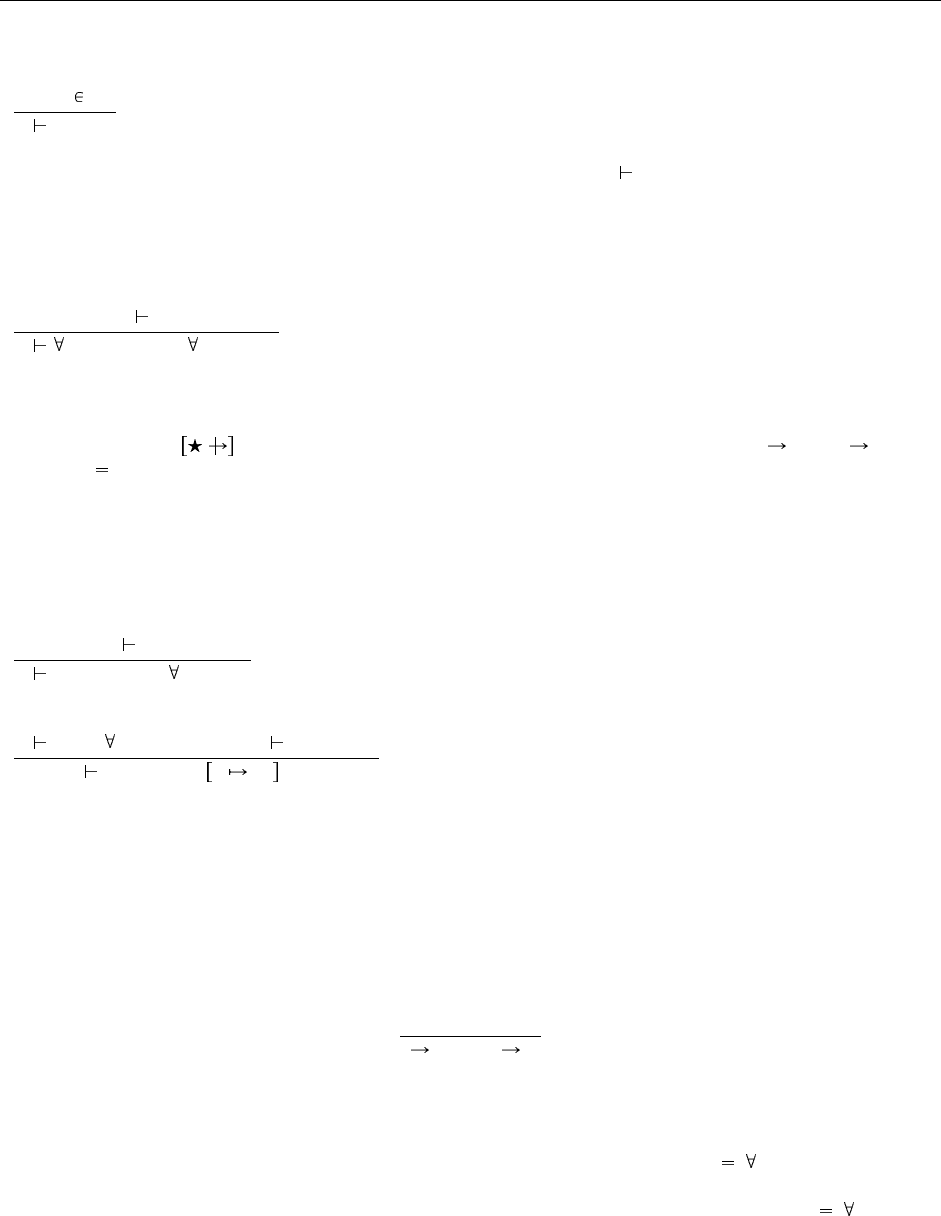
26.2. Определения 305
эти границы используются, чтобы обосновать шаги вида «типовая переменная X является подтипом ти-
па T, поскольку мы так предположили».
X<:T Γ
Γ X <: T
(S-TVar)
После добавления этого правила получается, что наследование стало трехместным отношением — то
есть, теперь каждое утверждение о наследовании будет иметь вид Γ S <: T, что читается «S является
подтипом T, предполагая Γ». Такое уточнение требует также добавления контекстов во все остальные
правила наследования (см. Рис. 26.1).
Помимо нового правила для переменных, требуется также добавить правило наследования для срав-
нения универсальных типов (S-All). На Рис. 26.1 приведен более простой вариант, называемый ядерное
правило. Согласно этому правилу, границы двух сравниваемых кванторов должны быть одинаковы.
Γ, X<:U
1
S
2
<: T
2
Γ X<:U
1
.S
2
<: X<:U
1
.T
2
(S-All)
Термин «ядерное» восходит к исходной статье Карделли и Вегнера (Cardelli and Wegner 1985), где этот
вариант F
<:
назывался Ядерная Fun.
Упражнение 26.2.1 : Нарисуйте дерево вывода наследования, показывающее B Y <: X B в кон-
тексте Γ B<:Top, X<:B, Y<:X.
26.2.4. Типизация
Требуется также уточнить правила типизации для обыкновенных универсальных типов. Эти рас-
ширения не представляют труда: в правиле введения для ограниченной квантификации мы переносим
границу из абстракции типа в контекст на время проверки типов в теле,
Γ, X<:T t
2
: T
2
Γ λX<:T.t
2
: X<:T.T
2
(T-TAbs)
а в правиле удаления мы проверяем, что данный нам тип на самом деле удовлетворяет граничному
условию:
Γ t
1
: X<:T
11
.T
12
Γ T
2
<: T
11
Γ t
1
[T
2
] : X T
2
X.T
12
(T-TApp)
26.2.5. Полная F
<:
В ядерной F
<:
два типа с кванторами можно сравнивать только в том случае, когда у них оди-
наковые верхние границы. Если мы рассматриваем квантор как своего рода функциональный тип
(элементами которого являются функции из типов в термы), то ядерное правило соответствует
«ковариантному» ограничению стандартного правила наследования для функциональных типов, где
запрещено изменять область определения исходного типа в подтипах:
S
2
<: T
2
U S
2
<: U T
2
Такое ограничение выглядит неестественным, как для обычных функций, так и для кванторов. Анало-
гия подстказывает, что следует уточнить правило S-All и позволить контравариантное наследование
на «левой стороне» ограниченных кванторов, как показано на Рис. 26.2.
Интуитивно полную версию правила S-All можно понимать так: тип T X<:T
1
.T
2
описывает
совокупность функций, переводящих типы в значения, так что каждая из них отображает подтипы
T
1
в экземпляры T
2
. Если T
1
— подтип S
1
, то область определения T меньше, чем у S X<:S
1
.S
2
,
так что S оказывается более сильным ограничением и описывает меньшую совокупность полиморфных
значений. Более того, если для каждого типа U, подходящего как аргумент функциям из обеих совокуп-
ностей (т. е., удовлетворяющего более жесткому ограничению U <: T
1
), U-конкретизация S
2
является
подтипом U-конкретизации T
2
, то ограничение S «поточечно сильнее», и, опять же, описывает меньшую
совокупность значений.
rev. 104
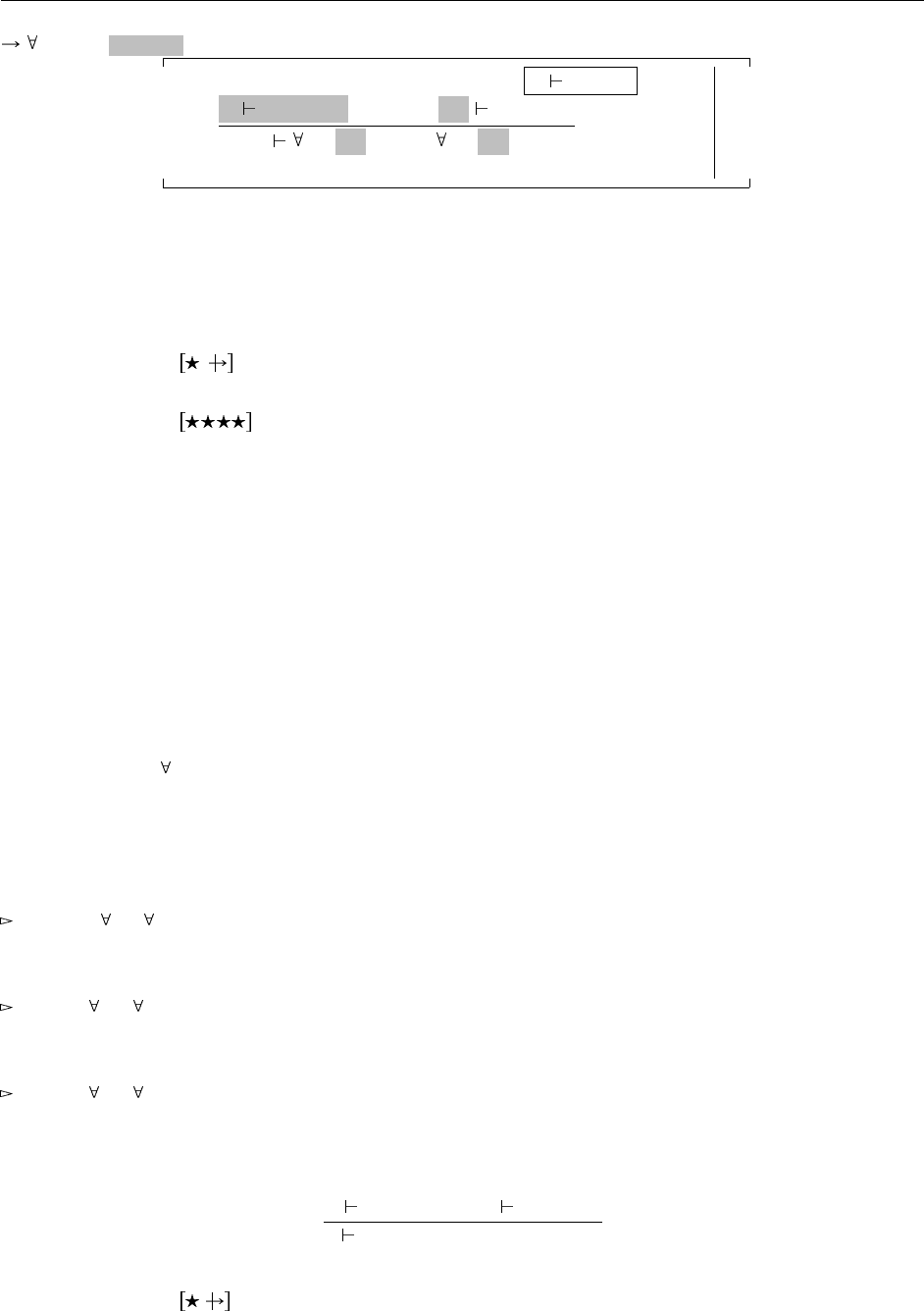
306 26.3. Примеры
<: Top полная Расширяет F
<:
(26.1)
Новые правила наследования Γ S <: T
Γ T
1
<: S
1
Γ, X<: T
1
S
2
<: T
2
Γ X<: S
1
.S
2
<: X<: T
1
.T
2
(S-All)
Рис. 26.2. «Полная» ограниченная квантификация
Система, в которой принято только ядерное правило наследования для кванторных типов, называ-
ется Ядерной F
<:
. Та же система с полным правилом наследования для кванторов называется Полной
F
<:
. Простое имя F
<:
неоднозначно и может относиться к любой из этих двух систем.
Упражнение 26.2.2 : Приведите несколько примеров пар типов, которые в полной F
<:
связаны
отношением наследования, а в ядерной F
<:
нет.
Упражнение 26.2.3 : Можете ли Вы найти какие-либо полезные примеры, обладающие таким
свойством?
26.3. Примеры
В этом разделе дается несколько небольших примеров программирования на F
<:
. В этих примерах
мы пытаемся продемонстрировать свойства системы, а не ее практическое применение; более крупные
расширенные примеры можно найти в последующих главах (27 и 32). Все примеры этой главы будут
работать как в ядерной, так и в полной F
<:
.
26.3.1. Кодирование типов-произведений
В §23.4.3 мы показали, как закодировать пары чисел в Системе F. Этот код легко обобщается на
пары произвольных типов: элементы типа
Pair T
1
T
2
= X . ( T
1
-> T
2
-> X) -> X;
представляют пары из T
1
и T
2
. Конструктор pair и деструкторы fst и snd определяются как показано
ниже. (Приписывание типа в определении pair помогает интерпретатору распечатать тип подобающим
образом.)
pair = λX . λY . λx:X. λy : Y. (λR. λp :X ->Y -> R . p x y ) as Pair X Y;
pair : X. Y. X -> Y -> Pair X Y
fst = λX . λY. λp: Pair X Y. p [X ] (λx :X. λy : Y. x );
fst : X . Y . Pair X Y -> X
snd = λX . λY. λp: Pair X Y. p [Y ] (λx :X. λy : Y. y );
snd : X . Y . Pair X Y -> Y
Понятно, что такой же способ кодирования можно использовать и в F
<:
, поскольку F
<:
содержит все
конструкции Системы F. Интереснее, однако, что это кодирование обладает некоторыми естественными
свойствами в части наследования. В частности, ожидаемое правило наследования для пар
Γ S
1
<: T
1
Γ S
2
<: T
2
Γ Pair S
1
S
2
<: Pair T
1
T
2
прямо из него следует.
Упражнение 26.3.1 : Покажите это.
rev. 104

26.3. Примеры 307
26.3.2. Кодирование записей
Интересно заметить, что записи и типы записей — включая законы наследования для них, — можно
закодировать в чистой F
<:
. Представленный здесь способ кодирования был открыт Карделли (Cardelli
1992).
Для начала мы определяем гибкие кортежи. Они называются «гибкими», поскольку при наследо-
вании разрешается расширять их справа, в отличие от обыкновенных кортежей.
Определение 26.3.2 Для каждого n 0 и типов с T
1
по T
n
, пусть
{T
i
i 1..n
}
def
Pair T
1
(Pair T
2
...(Pair T
n
Top)...)
В частности:
def
Top. Подобным образом, для термов с t
1
по t
n
, пусть
{t
i
i 1..n
}
def
pair t
1
(pair t
2
...(pair t
n
top)...)
(ради краткости мы опускаем аргументы-типы конструктора pair. В качестве терма top исполь-
зуется какой-нибудь произвольный элемент Top — т. е., произвольный замкнутый правильно типи-
зированный терм.) Проекция t.n (опять, с пропуском типовых аргументов) равна
fst (snd (snd...(snd
n 1 раз
t)...)
Из такого сокращения мы немедленно получаем следующие правила для наследования и типизации
гибких кортежей:
Γ
i 1..n
S
i
<: T
i
Γ {S
i
i 1..n
} <: {T
i
i 1..n
}
Γ
i 1..n
t
i
: T
i
Γ {t
i
i 1..n
} : {T
i
i 1..n
}
Γ t : {T
i
i 1..n
}
Γ t.i : T
i
Пусть теперь имеется счетное множество меток L, и для него задан полный порядок при помощи
биективной функции метка-с-индексом : N L. Определяем записи следующим образом.
Определение 26.3.3 Пусть имеется L — конечное подмножество L, и для каждого l L задан тип
S
l
. Пусть максимальный индекс элементов L равен m и
ˆ
S
i
S
l
если метка-с-индексом i l L
Top если метка-с-индексом i L.
Тип записей {l:S
l
l L
} определяется как гибкий кортеж {
ˆ
S
i
i 1..m
}. Аналогично, если для каждого l L
имеется терм t
l
, то
ˆ
t
i
t
l
если метка-с-индексом i l L
top если метка-с-индексом i L.
Значение записи {l=t
l
l L
} определяется как {
ˆ
t
i
i 1..m
}. Проекция t.l — просто проекция кортежа
t.i, где метка-с-индексом i l.
При таком кодировании выполняются все необходимые правила типизации и наследования для за-
писей (S-RcdWidth, S-RcdDepth, S-RcdPerm, T-Rcd и T-Proj с Рис. 15.2 и 15.3). Однако интерес
к подобному построению в основном теоретический — с практической точки зрения, опора на глобаль-
ное упорядочение имен полей является серьезным недостатком, поскольку получается, что в языке с
раздельной компиляцией нельзя нумеровать поля отдельно в каждом модуле, а нужно это сделать один
раз для всех полей, т. е., при компоновке.
rev. 104
308 26.3. Примеры
26.3.3. Кодирование по Чёрчу с наследованием
В качестве последней демонстрации выразительной силы F
<:
давайте рассмотрим, что получается
при добавлении ограниченной квантификации к кодированию чисел по Чёрчу в Системе F (§23.4.3).
Там тип чисел Чёрча был
CNat = X. (X - >X) -> X -> X ;
Неформально можно прочитать этот тип так: «Скажите мне тип результата T; потом дайте мне функ-
цию на T и ‘базовый элемент’ T, и тогда я верну вам еще один элемент T, полученный n-кратным
применением данной мне функции к данному мне исходному элементу».
Можно обобщить это определение, добавив два ограниченных квантора и уточнив тип параметров
s и z.
SNat = X <: Top . S <: X . Z <: X . (X ->S) -> Z -> X;
Этот тип можно интуитивно читать так: «Дайте мне тип обобщенного результата X и два подтипа S и Z.
Потом дайте мне функцию, отображающую все множество X на подмножество S, а также элемент осо-
бого множества Z, и я верну вам элемент X, получаемый n-кратным применением функции к базовому
элементу».
Чтобы понять, почему это уточнение интересно, рассмотрим следующий, несколько отличающийся
тип:
SZero = X <: Top . S <: X . Z <: X . (X ->S) -> Z -> Z;
Несмотря на то, что SZero имеет почти такой же вид, как SNat, он говорит о поведении своих элементов
намного больше, поскольку обещает, что окончательный результат будет элементом Z, а не просто X.
В сущности, есть только один способ обеспечить такое поведение — а именно, вернуть сам аргумент z.
Другими словами, значение
szero = λX . λS <: X. λZ <: X . λs:X -> S . λz :Z. z;
szero : SZero
является единственным элементом типа SZero (в том смысле, что всякий другой элемент типа SZero
по поведению неотличим от szero). Поскольку SZero — подтип SNat, имеем также szero : SNat.
С другой стороны, другой подобный тип
SPos = X <: Top . S <: X. Z <: X. (X ->S ) -> Z -> S;
имеет больше различных элементов, например,
sone = λX . λS <: X. λZ <: X . λs:X -> S . λz:Z. s z;
stwo = λX . λS <: X. λZ <: X . λs:X -> S . λz:Z. s (s z );
st hree = λX. λS <: X . λZ <: X. λs:X ->S. λz : Z. s ( s ( s z ));
и так далее. Действительно, SPos содержит все элеменыты SNat за исключением szero.
Подобным образом можно уточнить типы операций над числами Чёрча. Например, с помощью
системы типов можно проверить, что результатом функции-последователя всегда является положи-
тельное число.
ssucc = λn : SNat .
λX . λS <: X. λZ <: X . λs:X -> S . λz :Z.
s (n [X] [S ] [ Z ] s z );
ssucc : SNat -> SPos
Точно так же, уточняя типы параметров, мы можем написать функцию plus так, чтобы процедура
проверки типов приписала ей тип SPos SPos SPos.
sp luspp = λn: SPos . λm: SPos .
λX . λS <: X. λZ <: X . λs:X -> S . λz :Z.
n [X] [S ] [ S ] s ( m [ X ] [ S] [ Z] s z );
sp luspp : SPos -> SPos -> SPos
rev. 104

26.4. Безопасность 309
Упражнение 26.3.4 : Напишите еще один вариант функции plus, отличающийся от приведен-
ного выше только аннотациями типов, и имеющий тип SZero SZero SZero. Напишите вариант
с типом SPos SNat SPos.
Последний пример и упражнение к нему обращают внимание на интересный вопрос. Ясно, что мы
не хотим писать несколько различных версий функции plus с различными именами, а потом решать,
которую из них применить в соответствии с типами аргументов: хотелось бы иметь одну версию plus,
в типе которой учитывались бы все эти возможности — нечто вроде
plus : SZero - > SZero - > SZero
SNat SPos SPos
SPos SNat SPos
SNat SNat SNat
где запись t : S T означает «терм t имеет одновременно типы S и T». Желание поддержать в язы-
ке такую перегрузку типов привело к исследованию систем, сочетающих типы-пересечения (15.7) с
ограниченной квантификацией. См. (Pierce 1997b).
Упражнение 26.3.5 Рекомендуется, : Действуя по образцу SNat и компании, обобщите тип
Чёрчевых булевских значений CBool (§23.4.3) до типа SBool с двумя подтипами STrue и SFalse.
Напишите функцию notft с типом SFalse STrue и функцию nottf с типом STrue SFalse.
Упражнение 26.3.6 : В начале главы мы упомянули, что наследование и полиморфизм можно
совместить более простым и ортогональным способом, чем в F
<:
. Начинаем с Системы F (возможно,
с добавлением записей и т. п.) и добавляем отношение наследования (как в простом типизированном
лямбда-исчислении с наследованием), но оставляем квантификацию неограниченной. Единственным
расширением отношения наследования будет ковариантное правило наследования для тел обыкновен-
ных кванторов:
S <: T
X.S <: X.T
Какие примеры из данной главы можно сформулировать в рамках этой более простой системы?
26.4. Безопасность
Свойство сохранения типов можно доказать обычным способом как для ядерного, так и для
полного варианта F
<:
. Здесь мы приводим подробное доказательство для ядерной F
<:
; для полной
F
<:
рассуждение выглядит почти так же. Однако когда в Главе 28 мы рассмотрим алгоритмы проверки
типов и наследования, окажется, что два варианта различаются сильнее, чем можно предположить по
простым доказательствам из этой главы. Мы увидим, что во многих деталях полная система намного
труднее поддается анализу, чем ядерная, и даже что полная система не обладает некоторыми полезны-
ми свойствами (включая разрешимость проверки типов!), которые в ядерной системе присутствуют.
Вначале мы устанавливаем некоторые предварительные технические леммы, касающиеся отноше-
ний типизации и наследования. Все они доказываются обычной индукцией по деревьям вывода.
Лемма 26.4.1 Перестановка : Предположим, что Γ — правильно сформированный контекст, а ∆
— перестановка Γ, — то есть, ∆ связывает те же самые переменные, что и Γ, и порядок этих
связываний в ∆ сохраняет области их видимости из Γ, в смысле, что, если одно связывание в Γ
вводит типовую переменную, которая упоминается в другом связывании, расположенном правее, то
в ∆ порядок этих связываний сохраняется.
1. Если Γ t : T, то ∆ t : T.
2. Если Γ S <: T, то ∆ S <: T.
Лемма 26.4.2 Ослабление :
1. Если Γ t : T и контекст Γ, x:U сформирован правильно, то Γ, x:U t : T.
rev. 104

310 26.4. Безопасность
2. Если Γ t : T и контекст Γ, X<:U сформирован правильно, то Γ, X<:U t : T.
3. Если Γ S <: T и контекст Γ, x:U сформирован правильно, то Γ, x:U S <: T.
4. Если Γ S <: T и контекст Γ, X<:U сформирован правильно, то Γ, X<:U S <: T.
Упражнение 26.4.3 : В каком месте доказательство свойства ослабления зависит от перестанов-
ки?
Лемма 26.4.4 Усиление для термовых переменных в деревьях вывода наследования : Ес-
ли Γ, x:T, ∆ S <: T, то Γ, ∆ S <: T.
Доказательство: Утверждение очевидно: предположения о типизации при выводе наследования не
играют никакой роли.
Как обычно, доказательство сохранения типов опирается на несколько лемм, связывающих подста-
новку с отношениями типизации и наследования.
Лемма 26.4.5 Сужение :
1. Если Γ, X<:Q, ∆ S <: T и Γ P <: Q, то Γ, X<:P, ∆ S <: T.
2. Если Γ, X<:Q, ∆ t : T и Γ P <: Q, то Γ, X<:P, ∆ t : T.
Эти леммы часто называют свойствами сужения, поскольку они связаны с ограничением (сужени-
ем) возможных значений переменной X.
Доказательство: Упражнение .
Затем, как обычно, требуется лемма, связывающая подстановку и отношение типизации.
Лемма 26.4.6 Подстановка сохраняет типизацию : Если Γ, x:Q, ∆ t : T и Γ q : Q, то
Γ, ∆ x q t : T.
Доказательство: Индукция по дереву вывода Γ, x:Q, ∆ t : T, с использованием свойств, доказанных
ранее.
Поскольку при вычислении мы будем иногда подставлять типы вместо типовых переменных, нам
требуется также лемма, связывающая подстановку типов с типизацией. Ее доказательство (а именно,
вариант T-Sub) зависит от новой леммы, свзывающей подстановку и наследование.
Определение 26.4.7 Запись X S Γ обозначает контекст, получаемый подстановкой S вместо X в
правых частях всех связываний в Γ.
Лемма 26.4.8 Подстановка типов сохраняет наследование : Если Γ, X<:Q, ∆ S <: T и Γ
P <: Q, то Γ, X P ∆ X P S <: X P T.
Обратите внимание, что требуется проводить подстановку для X только в той части окруже-
ния, которая следует за связыванием X, поскольку наши соглашения об областях видимости требуют,
чтобы типы слева от связывания X переменной X не содержали.
Доказательство: Индукция по дереву вывода Γ, X<:Q, ∆ S <: T. Интерес представляют только два
последних варианта:
Вариант S-Tvar: S Y Y<:T Γ, X<:Q, ∆
Нужно рассмотреть два подварианта. Если Y X, то результат немедленно следует из S-TVar.
Если же Y X, то имеем T Q и X P S Q, и тогда результат следует из S-Refl.
Вариант S-All: S Z<:U
1
,S
2
T Z<:U
1
.T
2
Γ, X<:Q, ∆, Z<:U
1
S
2
<: T
2
Согласно предположению индукции, Γ, X P ∆, Z<: X P U
1
X P S
2
<: X P T
2
. По прави-
лу S-All, Γ, X P ∆ Z<: X P U
1
. X P S
2
<: Z<: X P U
1
.T
2
, то есть, как и требуется,
Γ, X P ∆ X P Z<:U
1
.S
2
<: X P Z<:U
1
.T
2
.
Подобная же лемма связывает подстановку типов и типизацию.
rev. 104
