Пирс Б. Типы в языках программирования

Подождите немного. Документ загружается.

321

построить правильно типизированное кодирование классов с таким же операционным поведением) в

языке, где присутствует только ограниченная квантификация и инвариантный конструктор Ref?

rev. 104

322

rev. 104

Глава 28

Метатеория ограниченной

квантификации

В этой главе мы разрабатываем алгоритмы вычисления наследования и проверки типов для F

Изучается как ядерная, так и полная версия системы; ведут они себя по-разному. Некоторые свой-

ства присутствуют в обоих вариантах, но в полном доказываются сложнее, а другие характеристики

в полной F

попросту утрачиваются. Такова цена, которую приходится платить за большую вырази-

тельность этой системы.

Сначала, в §28.1 и §28.2, мы представляем алгоритм проверки типов, работающий в обеих системах.

Затем мы рассматриваем проверку наследования, сначала в §28.3 для ядерной системы, а потом в §28.4

для полной. В §28.5 продолжается обсуждение наследования в полной F

, и особое внимание уделяется

тому удивительному обстоятельству, что отношение наследования неразрешимо. В §28.6 мы показыва-

ем, что в ядерной F

имеются пересечения и объединения, а в полной нет. §28.7 касается некоторых

вопросов, связанных с ограниченными экзистенциальными типами, а в §28.8 мы рассматриваем, к чему

приводит добавление минимального типа Bot.

28.1. Выявление

В алгоритме проверки типов для простого типизированного лямбда-исчисления с наследованием из

§16.2 ключевой идеей было вычислять минимальный тип для каждого терма, исходя из минимальных

типов его подтермов. Ту же самую базовую идею можно использовать и для F

, однако нужно при-

нять во внимание небольшую сложность, возникающую из-за наличия в системе типовых переменных.

Рассмотрим терм

f = λX <: Nat - > Nat . λy : X . y 5;

f : X <: Nat -> Nat . X -> Nat

Ясно, что этот терм правильно типизирован, поскольку тип переменной y в применении y 5 может быть

повышен до Nat Nat по правилу T-Sub. Однако минимальный тип y равен X, и это не функциональ-

ный тип. Чтобы определить минимальный тип всего терма-применения, нужно найти минимальный

функциональный тип для y — т. е., минимальный функциональный тип, являющийся надтипом типо-

вой переменной X. Неудивительно, что такой тип можно найти, повышая минимальный тип y, пока он

не превартится в нечто отличное от типовой переменной.

Мы используем формальную запись Γ S T (читаемую «S выявляется как T в контексте Γ»),

обозначая таким образом утверждение «T — минимальный надтип S, не являющийся переменной».

Выявление определяется через циклическое повышение типовых переменных, как показано на Рис. 28.1.

В этой главе изучается чистая система F

(Рис. 26.1). Соответствующий интерпретатор на OCaml называется

purefsub; интерпретатор fullfsub включает также экзистенциальные типы (24.1) и некоторые расширения из Главы 11.

323

324 28.2. Минимальная типизация

<: Top

Выявление Γ T T

X<:T Γ Γ T T

Γ X T

(XA-Promote)

T не является типовой переменной

Γ T T

(XA-Other)

Рис. 28.1. Алгоритм выявления для F

<: Top Расширяет λ

(16.3)

Алгоритмическая типизация Γ t : T

x:T Γ

Γ x : T

(TA-Var)

Γ, x:T t

: T

Γ λx:T

: T

(TA-Abs)

Γ t

: T

Γ T

Γ t

: T

Γ T

<: T

Γ t

: T

(TA-App)

Γ, X<:T

: T

Γ λX<:T

: X<:T

(TA-TAbs)

Γ t

: T

Γ T

X<:T

Γ T

<: T

Γ t

] : X T

(TA-TApp)

Рис. 28.2. Алгоритмическая типизация для F

Нетрудно убедиться, что эти правила дают нам всюду определенную функцию. Более того, резуль-

татом выявления типа всегда будет наименьший надтип, отличный от переменной. Например, если

Γ X<:Top, Y<:Nat Nat, Z<:Y, W<:Z, то

Γ Top Top Γ Y Nat Nat Γ W Nat Nat

Γ X Top Γ Z Nat Nat

Основные свойства выявления можно описать следующим образом.

Лемма 28.1.1 Выявление : Допустим, Γ S T. Тогда

1. Γ S <: T

2. Если Γ S <: U и U не является переменной, то Γ T <: U.

Доказательство: Часть (1) доказывается индукцией по деревьям вывода Γ S T, часть (2) индук-

цией по деревьям вывода Γ S <: U.

28.2. Минимальная типизация

Алгоритм нахождения минимальных типов строится по тем же принципам, что и для простого

типизированного лямбда-исчисления с наследованием, но есть одна дополнительная деталь: когда мы

проверяем тип в терме-применении, мы сначала вычисляем минимальный тип левой стороны, а затем

выявляем его, получая функциональный тип, как показано на Рис. 28.2. Если же при выявлении левой

стороны применения не получается функционального типа, то правило TA-App оказывается непри-

менимо, и терм типизирован неверно. Подобным же образом мы проверяем типы в применении типа:

выявляем левую сторону и надеемся при этом получить кванторный тип.

Доказательство корректности и полноты этого алгоритма по отношению к исходнымправилам типи-

зации не представляют труда. Мы приводим доказательство для ядерной F

(рассуждение для полной

строится подобным же образом; см. Упражнение 28.2.3).

rev. 104

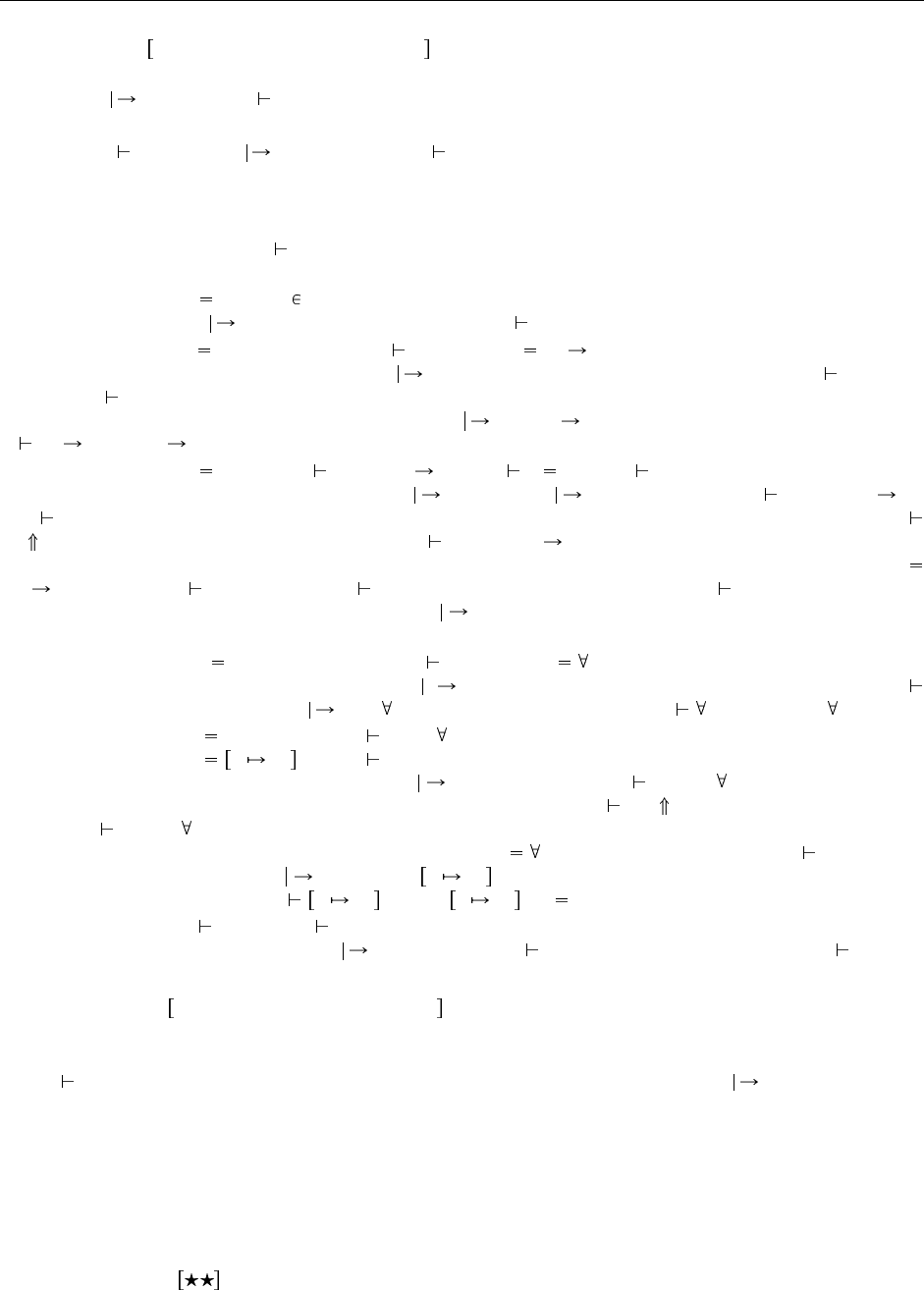
28.2. Минимальная типизация 325

Теорема 28.2.1 Минимальаная типизация :

1. Если Γ t : T, то Γ t : T.

2. Если Γ t : T, то Γ t : M, причем Γ M : T.

Доказательство: Часть (1) представляет собой несложную индукцию по алгоритмическим выводам,

с использованием части (1) Леммы 28.1.1 для вариантов с применениями. В части (2) проводится

индукция по дереву вывода Γ t : T, с разбором вариантов последнего правила в выводе. Наиболее

интересны варианты T-App и T-TApp.

Вариант T-Var: t x x:T Γ

По правилу TA-Var, Γ x : T. По правилу S-Refl, Γ T <: T.

Вариант T-Abs: t λx:T

Γ, x:T

: T

T T

Согласно предположению индукции, Γ, x:T

: M

для некоторого M

, причем Γ, x:T

<: T

— т. е., Γ M

<: T

, поскольку наследование не зависит от связываний термовых переменных в

контексте (Лемма 26.4.4). По правилу TA-Abs, Γ t : T

. По правилям S-Refl и S-Arrow,

Γ T

<: T

Вариант T-App: t t

Γ t

: T

Γ T T

Γ t

: T

Согласно предположению индукции, имеем Γ t

: M

и Γ t

: M

, причем Γ M

<: T

и Γ M

<: T

. Пусть наименьший надтип M

, не являющийся переменной, будет N

, т. е., Γ

. Согласно части (2) Леммы 28.1.1, Γ N

<: T

. Поскольку мы знаем, что N

— не

переменная, лемма об обращении для отношения наследования (26.4.10) сообщает нам, что N

, причем Γ T

<: N

и Γ N

<: T

. По транзитивности, Γ M

<: N

, так что

применимо правило TA-App, и оно дает нам Γ t

: N

. Все требования теоремы при этом

оказываются соблюдены.

Вариант T-TAbs: t λX<:T

Γ, X<:T

: T

T X<:T

Согласно предположению индукции, Γ, X<:T

: M

для некоторого M

, причем Γ, X<:T

<: T

. По правилу TA-TAbs, Γ t : X<:T

. По правилу S-All, Γ X<:T

<: X<:T

Вариант T-TApp: t t

] Γ t

: X<:T

T X T

Γ T

<: T

Согласно предположению индукции, имеем Γ t

: M

, причем Γ M

<: X<:T

. Пусть N

— наименьший надтип M

, не являющийся переменной, т. е., Γ M

. По лемме о выявлении

(28.1.1), Γ N

<: X<:T

. Но мы знаем, что N

— не переменная, так что, по лемме об обра-

щении для отношения наследования (26.4.10), имеем N

X<:T

, причем Γ, X<:T

<: T

Правило TA-TApp дает нам Γ t

] : X T

, а поскольку наследование сохраняется при

подстановке (Лемма 26.4.8), Γ X T

<: X T

Вариант T-Sub: Γ t : S Γ S <: T

Согласно предположению индукции, Γ t : M, причем Γ M <: S. По транзитивности, Γ M <: T.

Следствие 28.2.2 Разрешимость типизации : Отношение типизации для ядерной F

разрешимо,

если имеется разрешающая процедура для отношения наследования.

Доказательство: Для любых Γ и t мы можем проверить, существует ли какой-либо тип T, такой

что Γ t : T, породив при помощи алгоритмических правил доказательство Γ t : T. Если дока-

зательство прошло успешно, то полученный T является также типом для t согласно исходному от-

ношению типизации, по части (1) Теоремы 28.2.1. Если нет, то из части (2) Теоремы 28.2.1 следует,

что t не имеет типа в исходном отношении типизации. Наконец, заметим, что алгоритмические

правила типизации соответствуют всегда завершающемуся алгоритму, поскольку они управляются

синтаксисом (к каждому данному терму t применимо не более одного правила) и всегда уменьшают

размер t в направлении снизу вверх.

Упражнение 28.2.3 : Как нужно изменить приведенное выше доказательство, чтобы оно рабо-

тало с полной F

rev. 104

326 28.3. Наследование в Ядерной F

28.3. Наследование в Ядерной F

В §16.1 мы обратили внимание, что декларативное отношение наследования для простого типи-

зированного лямбда-исчисления с наследованием не является управляемым синтаксисом — т. е., его

невозможно прочесть как алгоритм, распознающий наследование, — по двум причинам: (1) заключе-

ния правил S-Refl и S-Trans перекрываются с другими правилами (так что, если мы читаем правила

снизу вверх, мы не знаем, которое правило требуется применить), и (2) в предпосылках S-Trans упо-

минается метапеременная, которая не встречается в его заключении (и наивному алгоритму пришлось

бы ее значение как-то «угадывать»). Мы видели, как с этими проблемами можно справиться, просто

исключив неудобные для алгоритмизации правила из системы, но чтобы это сделать, нам сначала по-

требовалось немного подправить систему, сведя три раздельных правила наследования для записей в

одно.

Для ядерной F

ситуация похожа. Снова неудобными правилами являются S-Refl и S-Trans, и

мы получаем алгоритм путем их устранения и правки остающихся правил, чтобы они взяли на себя

обработку тех случаев, когда устраненные правила были необходимы.

В простом типизированном лямбда-исчислении с наследованием не было случаев, когда необходи-

мо было бы правило рефлексивности — его можно было просто отбросить, не повлияв на множество

выводимых утверждений о наследовании (Лемма 16.1.2, часть 1). Напротив, в F

утверждения о на-

следовании вида Γ X <: X доказываются только через рефлексивность. Так что когда мы удаляем

правило рефлексивности, вместо него следует добавить ограниченную аксиому рефлексивности, каса-

ющуюся только переменных.

Γ X <: X

Подобным образом, чтобы избавиться от правила S-Trans, следует сначала понять, какие случаи его

использования неустранимы. Здесь интерес представляет взаимодействие с правилом T-Var, позволя-

ющим использовать предположения о переменных при выводе утверждений о наследовании. Например,

если Γ W<:Top, X<:W, Y<:X, Z<:Y, то утверждение Γ Z <: W невозможно вывести, если в системе от-

сутствует правило S-Trans. В общем случае использование S-Trans, где левый подвывод является

экземпляром аксиомы S-TVar, как в

Z <: Y Γ

Γ Z <: Y

(S-TVar)

Γ Y <: W

Γ Z <: W

(S-Trans)

неустранимо.

К счастью, выводы такого вида — елинственный неустранимый класс случаев использования тран-

зитивности при выводе наследования. Это наблюдение можно выразить точно, введя новое правило

наследования

X<:U Γ Γ U <: T

Γ X <: T

охватывающее в точности эту форму поиска переменной, за которым следует применение транзитив-

ности, и показав, что замена этим правилом правил транзитивности и поиска переменной не влияет на

множество выводимых утверждений о наследовании.

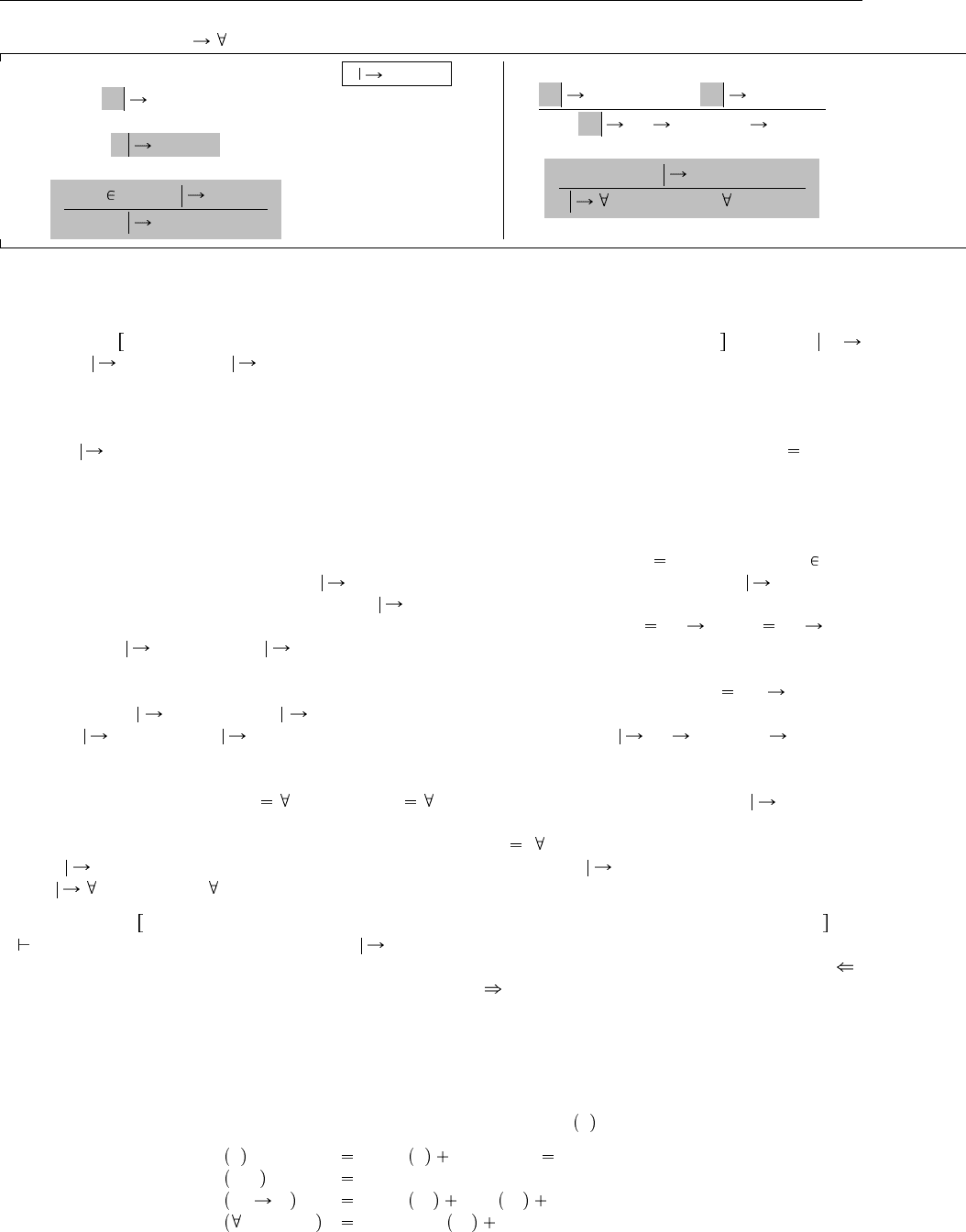
Эти изменения приводят нас к алгоритмическому отношению наследования для ядерной F

, изоб-

раженному на Рис. 28.3. Мы добавляем стрелку к концу символа штопора в алгоритмических утвер-

ждениях о наследовании, чтобы отличить их от исходной формы утверждений о наследовании, когда

речь в тексте идет об обеих разновидностях.

То, что новые правила SA-Refl-TVar и SA-Trans-TVar достаточны для замены старых правил

рефлексивности и транзитивности, показывают следующие две леммы.

Лемма 28.3.1 Рефлексивность алгоритмического отношения наследования : Для каждого

типа T можно доказать Γ T <: T.

Доказательство: Индукция по T.

rev. 104

28.3. Наследование в Ядерной F

327

<: Top Расширяет λ

(16.2)

Алгоритмическое наследование Γ S <: T

Γ S <: Top (SA-Top)

Γ X <: X (SA-Refl-TVar)

X<:U Γ Γ U <: T

Γ X <: T

(SA-Trans-TVar)

Γ T

<: S

Γ S

<: T

Γ S

<: T

(SA-Arrow)

Γ, X<:U

<: T

Γ X<:U

<: X<:U

(SA-All)

Рис. 28.3. Алгоритмическое отношение наследования для ядерной F

Лемма 28.3.2 Транзитивность алгоритмического отношения наследования : Если Γ

S <: Q и Γ Q <: T, то Γ S <: T.

Доказательство: Индукция по сумме размеров двух деревьев вывода. Имея два подвывода, мы рас-

сматриваем последние правила в обоих из них.

Если правый подвывод представляет собой экземпляр SA-Top, то доказательство закончено, по-

скольку Γ S <: Top по правилу SA-Top. Если левый подвывод — экземпляр SA-Top, то Q Top, и,

рассматривая алгоритмические правила, мы видим, что и правый подвывод обязан быть экземпляром

SA-Top.

Если какой-либо подвывод является экземпляром SA-Refl-TVar, то, опять же, все доказано,

поскольку другое поддерево будет в точности являться желаемым результатом.

Если левый подвывод завершается экземпляром SA-Trans-TVar, то S Y, причем Y<:U Γ, и

у нас есть подвывод с заключением Γ U <: Q. Согласно предположению индукции, Γ U <: T, и,

снова по правилу SA-Trans-TVar, имеем Γ Y <: T, как и требуется.

Если левое поддерево заканчивается экземпляром SA-Arrow, имеем S S

и Q Q

, с

подвыводами Γ Q

<: S

и Γ S

<: Q

. Однако, поскольку мы уже рассмотрели вариант, когда

правый подвывод представляет собой SA-Top, единственная оставшаяся возможность состоит в

том, что этот вывод также заканчивается на SA-Arrow, а значит, имеем T T

и еще

два подвывода Γ T

<: Q

и Γ Q

<: T

. Теперь дважды применяем предположение индукции,

получая Γ T

<: S

и Γ S

<: T

. Наконец, SA-Arrow дает нам Γ S

<: T

, как и

требуется.

В случае, когда левый подвывод заканчивается экземпляром SA-All, рассуждение проходит по-

добным же образом. Имеем S X<:U

и Q X<:U

, а также подвывод Γ, X<:U

<: Q

Снова, поскольку мы уже рассмотрели вариант, когда правый подвывод представляет собой SA-

Top, он должен заканчиваться на SA-All; так что T X<:U

, причем имеется подвывод

Γ, X<:U

<: T

. Из предположения индукции получаем Γ, X<:U

<: T

, и, по правилу SA-

All, Γ X<:U

<: X<:U

Теорема 28.3.3 Корректность и полнота алгоритмического отношения наследования :

Γ S <: T тогда и только тогда, когда Γ S <: T.

Доказательство: В обоих направлниях проводится индукция по деревьям вывода. Корректность ( )

не представляет труда. При доказательстве полноты ( ) используются Леммы 28.3.1 и 28.3.2.

Наконц, требуется проверить, что правила для наследования определяют тотальный алгоритм —

т. е., алгоритм, завершающийся при любых данных на входе. Мы делаем это, присваивая каждому

утверждению о наследовании вес, и проверяя, что каждое алгоритмическое правило имеет заключение

со строго большим весом, чем у предпосылок.

Определение 28.3.4 Вес типа T в контексте Γ, обозначаемый вес

T , определяется так:

вес

X вес

U 1 если Γ Γ

, X <: U, Γ

вес

Top 1

вес

X<:T

вес

Γ,X<:T

rev. 104

328 28.4. Наследование в Полной F

<: Top полная Расширяет λ

(28.3)

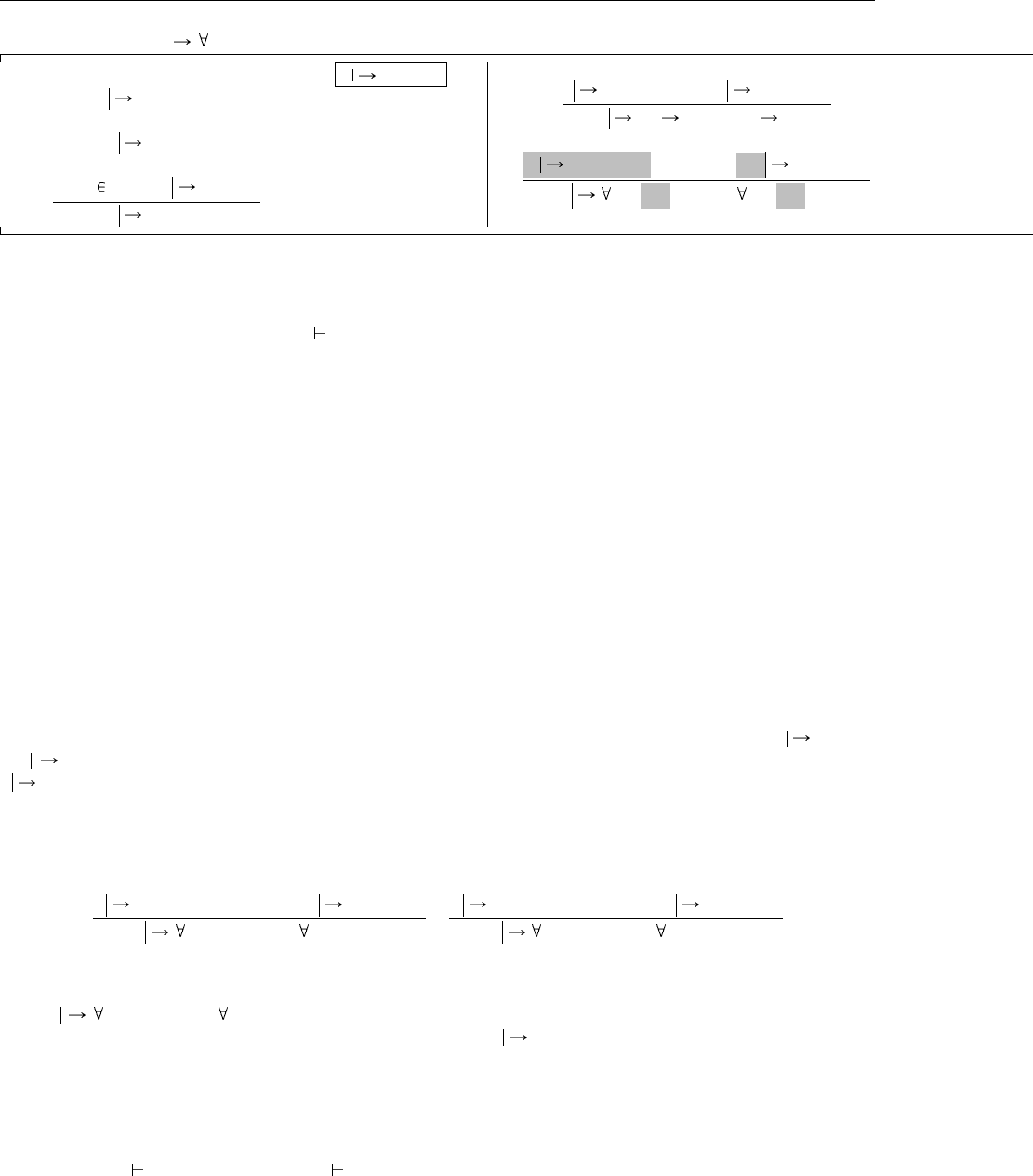
Алгоритмическое наследование Γ S <: T

Γ S <: Top (SA-Top)

Γ X <: X (SA-Refl-TVar)

X<:U Γ Γ U <: T

Γ X <: T

(SA-Trans-TVar)

Γ T

<: S

Γ S

<: T

Γ S

<: T

(SA-Arrow)

Γ T

<: S

Γ, X<: T

<: T

Γ X<: S

<: X<: T

(SA-All)

Рис. 28.4. Алгоритмическое отношение наследования для полной F

Вес утверждения о наследовании Γ S <: T есть сумма весов S и T в контексте Γ.

Теорема 28.3.5 Алгоритм проверки наследования завершается при любом вводе.

Доказательство: Вес заключения в любом экземпляре алгоритмического правила наследования всегда

строго больше, чем вес каждой из предпосылок.

Следствие 28.3.6 Отношение наследования в ядерной F

разрешимо.

28.4. Наследование в Полной F

Алгоритм проверки наследования для полной F

, приведенный на Рис. 28.4, почти такой же, как

для ядерной F

: единственное изменение заключается в замене SA-All на более гибкий вариант. Как

и в случае ядерной F

, корректность и полнота этого алгоритмического отношения относительно ис-

ходного отношения наследования прямо следуют из того, что алгоритмическое отношение рефлексивно

и транзитивно.

Рассуждение для рефлексивности остается в точности таким же, как раньше, однако доказательство

транзитивности оказывается много тоньше. Чтобы понять, почему это так, вспомним доказательство

транзитивности для ядерной F

из предыдущего раздела (Лемма 28.3.2). Там идея состояла в том, что-

бы взять два дерева вывода для отношения наследования, завершающиеся утверждениями Γ S <: Q

и Γ Q <: T, и показать, как переставить и пересобрать их поддеревья, получая при этом вывод

Γ S <: T без использования правила транзитивности, и используя (в качестве индуктивной гипоте-

зы) предположение, что то же самое можно проделать для выводов меньшего размера. Предположим

теперь, что у нас есть два подвывода, завершающиеся новым правилом SA-All:

Γ Q

<: S

Γ, X<:Q

<: Q

Γ X<:S

<: X<:Q

Γ T

<: Q

Γ, X<:T

<: T

Γ X<:Q

<: X<:T

Следуя схеме предыдущего доказательства, мы хотели бы воспользоваться предположением индукции,

чтобы сочетать левый и правый подвывод и получить единственный экземпляр SA-All с заключе-

нием Γ X<:S

<: X<:T

. Для левых подвыводов никаких сложностей нет; предположение

индукции дает нам свободный от транзитивности вывод Γ T

<: S

. Однако для правых подвыво-

дов предположение индукции неприменимо, поскольку контексты подвыводов различаются — верхняя

граница для X в одном из них равна Q

, а в другом T

К счастью, мы знаем, как сделать контексты одинаковыми: свойство сужения из Главы 26 (Лем-

ма 26.4.5) говорит, что истинное утверждение о наследовании остается истинным, если мы заменяем

граничный тип в контексте одним из его подтипов. Так что, казалось бы, можно просто сузить под-

вывод Γ, X<:Q

<: Q

до Γ, X<:T

<: Q

, и таким образом сделать предположение индукции

применимым.

Однако следует быть осторожными. Лемма 26.4.5 говорит, что можно взять произвольный вывод и

породить вывод с суженным заключением, однако она не гарантирует, что размер нового вывода будет

rev. 104

28.4. Наследование в Полной F

329

такой же, как у старого. В самом деле, рассмотрев доказательство этой леммы, мы увидим, что, как

правило, сужение порождает вывод большего размера, чем исходный, поскольку при этом всюду, где

аксиома S-TVar используется для поиска сужаемой переменной, вставляется копия произвольно боль-

шого вывода. Более того, эта операция вставки приводит к порождению новых экземпляров правила

транзитивности, а именно излишнесть этого правила в нашей текущей системе мы пытаемся доказать.

Чтобы справиться с этими сложностями, мы доказываем транзитивность и сужение совместно, с

предположением индукции, основанном на размере промежуточного типа Q для свойства транзитивно-

сти и размере исходного типа-границы Q для свойства сужения.

Прежде, чем начать основное доказательство, мы приводим несложную лемму, утверждающую,

что порядок добавления новых связываний типовых переменных в контекст не влияет на верность

выводимых утверждений о наследовании.

Лемма 28.4.1 Перестановка и ослабление :

1. Предположим, что ∆ является правильно сформированной перестановкой Γ (см. 26.4.1). Если

Γ S <: T, то ∆ S <: T.

2. Если Γ S <: T и dom ∆ dom Γ , то Γ, ∆ S <: T.

Доказательство: Прямолинейные индукции. Часть (1) используется в варианте SA-All части (2).

Лемма 28.4.2 Транзитивность и сужение для полной F

1. Если Γ S <: Q и Γ Q <: T, то Γ S <: T.

2. Если Γ, X<:Q, ∆ M <: N и Γ P <: Q, то Γ, X<:P, ∆ M <: N.

Доказательство: Обе части леммы доказываются одновременно, индукцией по размеру Q. На каждом

шаге индукции в доказательстве части (2) мы предполагаем, что часть (1) уже доказана для нашего

Q; часть (1) использует часть (2) только для типов Q строго меньшего размера.

1. Проводим внутреннюю индукцию по размеру первого данного нам вывода, и устраиваем анализ

последнего правила в обоих подвыводах. Все варианты, кроме одного, совпадают с доказатель-

ством Леммы 28.3.2; различие касается случая SA-All.

Если правый подвывод является экземпляром SA-Top, то доказательство закончено, поскольку

Γ S <: Top по правилу SA-Top. Если левый подвывод — экземпляр SA-Top, то Q Top

и, рассматривая алгоритмические правила, мы видим, что и правый подвывод тогда обязан

быть экземпляром SA-Top. Если какой-либо из подвыводов является экземпляром SA-Refl-

TVar, то, опять же, лемма доказана, поскольку другое поддерево будет в точности желемым

результатом.

Если левое поддерево заканчивается экземпляром правила SA-Trans-TVar, то имеем S Y,

причем Y<:U Γ, и есть подвывод утверждения Γ U : Q. По внутреннему предположению

индукции, Γ U <: T, и, снова по SA-Trans-TVar, Γ Y <: T, как нам и требуется.

Если левое поддерево заканчивается экземпляром правил SA-Arrow или SA-All, то, поскольку

вариант с правилом SA-Top в качестве правого подвывода уже рассмотрен, правый подвывод

должен завершаться тем же правилом, что и левый. Если это правило SA-Arrow, имеем

S S

, Q Q

и T T

с подвыводами Γ Q

<: S

, Γ S

<: Q

, Γ T

<: Q

и Γ Q

<: T

. Применяем часть (2) внешнего предположения индукции дважды (поскольку

как Q

, так и Q

меньше по размеру, чем Q) и получаем Γ T

<: S

и Γ S

<: T

. Наконец,

с помощью правила SA-Arrow получаем Γ S

<: T

В случае, когда оба подвывода заканчиваются на SA-All, имеем S X<:S

, Q X<:Q

и T X<:T

, и есть подвыводы

<: S

Γ, X<:Q

<: Q

Γ T

<: Q

Γ, X<:T

<: T

rev. 104

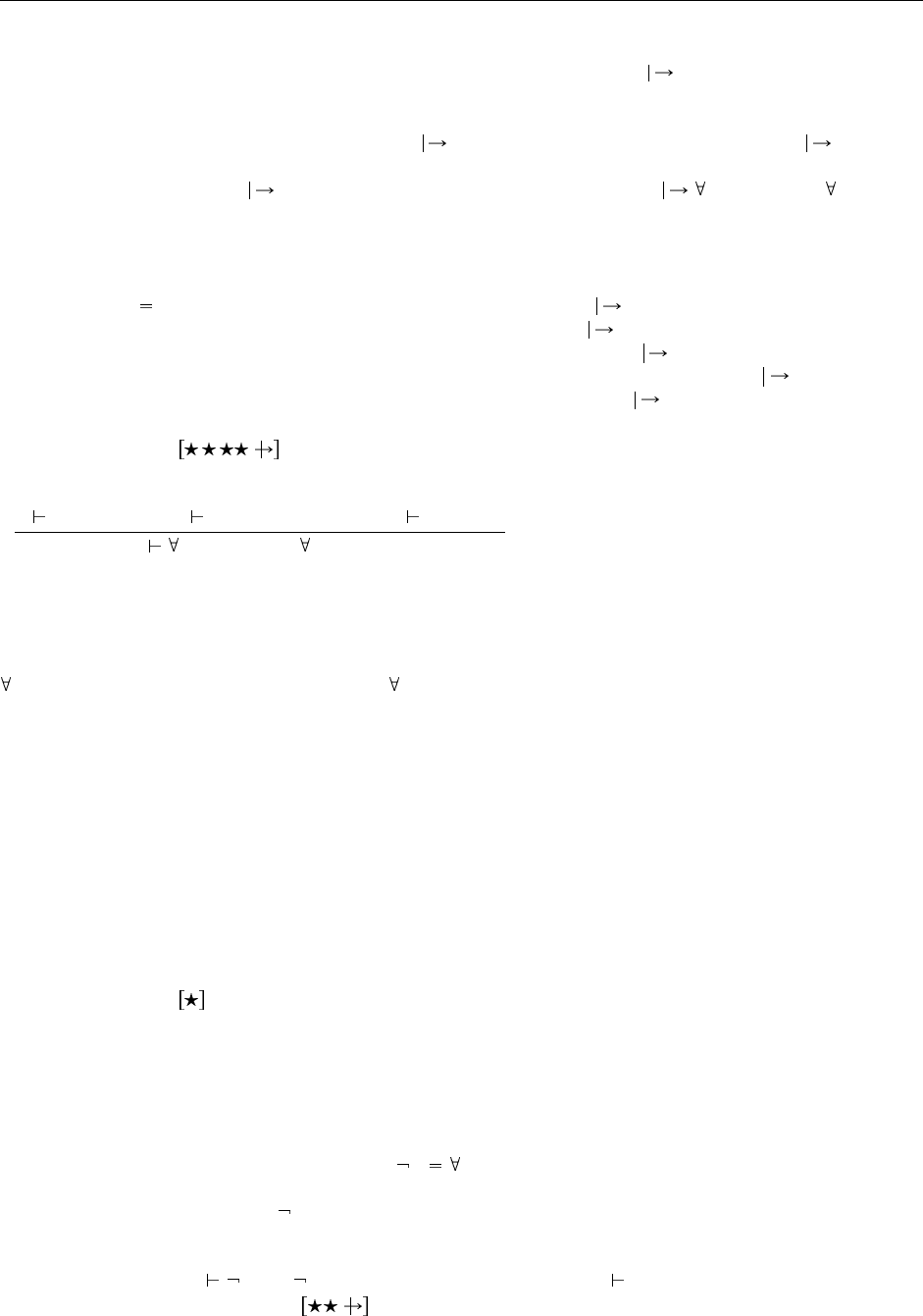
330 28.5. Неразрешимость Полной F

Согласно части (1) внешнего предположения индукции (поскольку Q

меньше по размеру, чем Q),

мы можем сочетать два подвывода для ограничений и получить Γ T

<: S

. Для тел кванто-

ров приходится приложить немного больше усилий, поскольку контексты не совсем совпадают.

Используем часть (2) внешнего предположения индукции (поскольку Q

меньше, чем Q) и сужа-

ем ограничение для X в подвыводе Γ, X<:Q

<: Q

, так что получается Γ, X<:T

<: Q

Теперь применима часть (1) внешнего предположения индукции (поскольку Q

меньше, чем Q);

она дает нам Γ, X<:T

<: T

. Наконец, по правилу SA-All, Γ X<:S

<: X<:T

2. Мы снова проводим индукцию по размеру первого данного подвывода, рассматривая варианты

последнего правила в нем. В большинстве вариантов нужно всего лишь очевидным образом ис-

пользовать внутреннее предположение индукции. Интерес представляет вариант SA-Trans-

TVar с M X, где в качестве подвывода мы имеем Γ, X<:Q, ∆ Q <: N. Применение к подвыводу

внутреннего предположения индукции дает нам Γ, X<:P, ∆ Q <: N. Кроме того, через ослаб-

ление (Лемма 28.4.1) второго данного вывода получаем Γ, X<:P, ∆ P <: Q. Теперь через часть

(1) внешнего предположения индукции (с тем же самым Q) имеем Γ, X<:P, ∆ P <: N. Нако-

нец, применяем правило SA-Trans-TVar и получаем Γ, X<:P, ∆ X <: N, как и требуется.

Упражнение 28.4.3 : Есть еще один осмысленный вариант правила наследования для кван-

торов, несколько более гибкий, чем правило ядерной F

, но существенно слабее, чем правило полной

Γ S

<: T

Γ T

<: S

Γ, X<:T

<: T

Γ X<:S

<: X<:T

(S-All)

Это правило близко к варианту ядерной F

, но требует не синтаксического совпадения границ

двух кванторов, а только их эквивалентности — каждый из них должен быть подтипом друго-

го. Разница между ядерным правилом и этим проявляется только тогда, когда мы обогащаем язык

какой-нибудь конструкцией, чьи правила наследования порождают нетривиальные классы эквива-

лентности между типами, например, записями. Скажем, в чистой ядерной F

с записями тип

X<:{a:Top,b:Top}.X не будет подтипом X<:{b:Top,a:Top}.X, а в системе с предлагаемым прави-

лом будет. Является ли наследование разрешимым в системе с таким правилом?

28.5. Неразрешимость Полной F

В предыдущем разделе мы установили, что алгоритмические правила наследования для полной

корректны и полны — то есть, что наименьшее отношение, замкнутое относительно этих правил,

содержит те же самые утверждения, что и наименьшее отношение, замкнутое относительно исходных

декларативных правил. Остается вопрос, завершается ли алгоритм, реализующий эти правила, при

всех возможных входах. К сожалению — и для многих, когда этот факт был обнаружен, он оказался

неприятным сюрпризом, — это не так.

Упражнение 28.5.1 : Раз алгоритмические правила для полной F

не определяют алгоритм, ко-

торый всегда завершается, то, очевидно, доказательство завершения для ядерной F

невозможно

перенести на правила полной системы. Где именно оно ломается?

Вот пример, найденный Гелли (Ghelli 1995), приводящий к незавершению алгоритма проверки на-

следования. Сначала определим следующее сокращение:

def

X<:S.X.

Ключевое свойство оператора состоит в том, что он позволяет обменивать местами стороны утвер-

ждений о наследовании.

Утверждение 28.5.2 Γ S <: T тогда и только тогда, когда Γ S <: T.

Доказательство: Упражнение .

rev. 104