Пирс Б. Типы в языках программирования
Подождите немного. Документ загружается.

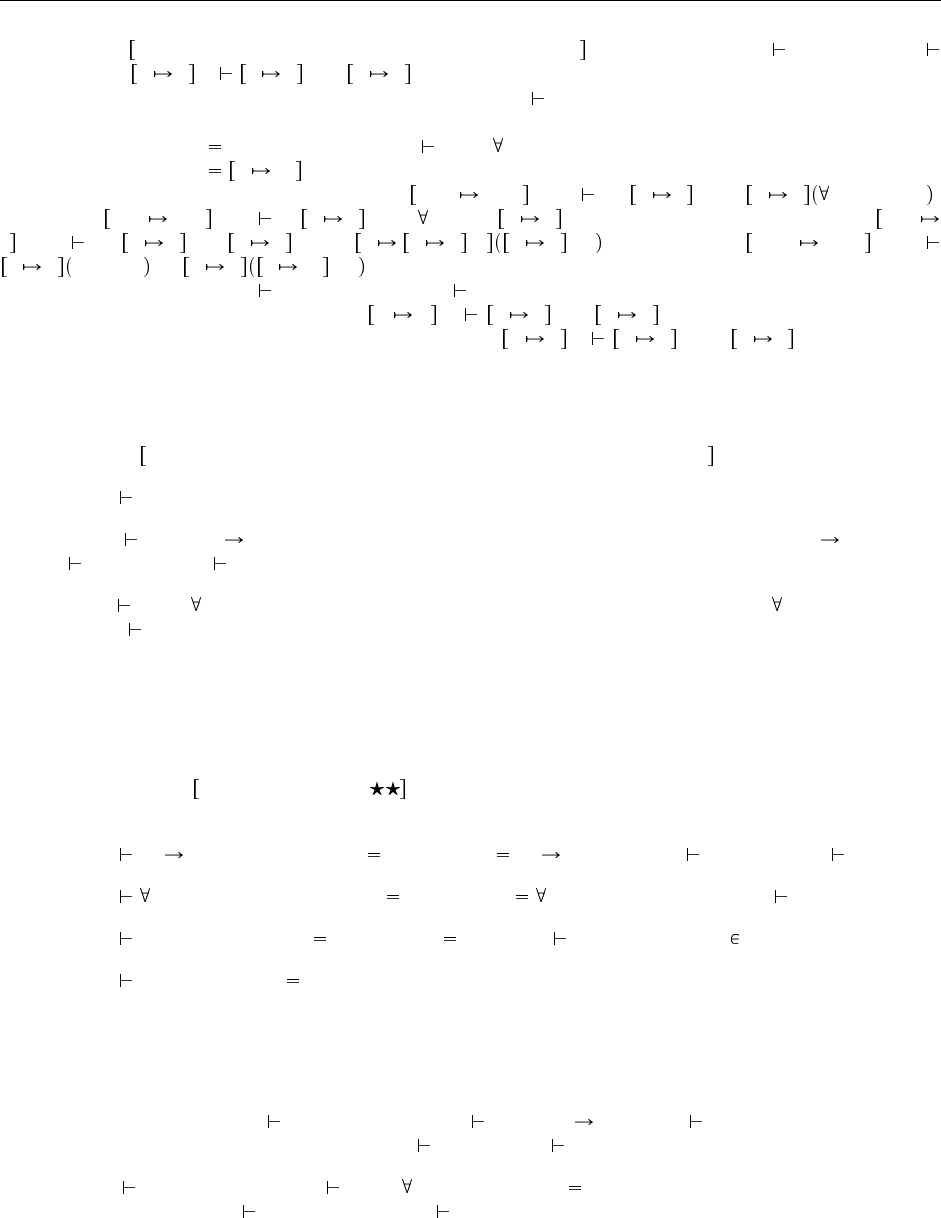
26.4. Безопасность 311
Лемма 26.4.9 Подстановка типов сохраняет типизацию : Если Γ, X<:Q, ∆ t : T и Γ
P <: Q, то Γ, X P ∆ X P t : X P T.
Доказательство: Индукция по дереву вывода Γ, X<:Q, ∆ t : T. Мы приводим только интересные
варианты.
Вариант T-TApp: t t
1
[T
2
] Γ, X<:Q, ∆ t
1
: Z<:T
11
.T
12
T Z T
2
T
12
Согласно предположению индукции, Γ, X P ∆ X P t
1
: X P Z<:T
11
.T
12
,
т. е., Γ, X P ∆ X P t
1
: Z<:T
11
. X P T
12
. По правилу T-TApp, Γ, X
P ∆ X P t
1
[ X P T
2
] : Z X P T
2
X P T
12
, т. е., Γ, X P ∆
X P t
1
[T
2
] : X P Z T
2
T
12
.
Вариант T-Sub: Γ, X<:Q, ∆ t : S Γ, X<:Q, ∆ S <: T
Согласно предположению индукции, Γ, X P ∆ X P t : X P T. По лемме о сохранении на-
следования при подстановке (Лемма 26.4.8) имеем Γ, X P ∆ X P S <: X P T, и требуемый
результат следует по правилу T-Sub.
Затем мы доказываем некоторые простые структурные свойства наследования.
Лемма 26.4.10 Обращение отношения наследования, справа налево :
1. Если Γ S <: X, то S является типовой переменной.
2. Если Γ S <: T
1
T
2
, то либо S — типовая переменная, либо S имеет вид S
1
S
2
, причем
Γ T
1
<: S
1
и Γ S
2
<: T
2
.
3. Если Γ S <: X<:U
1
.T
2
, то либо S — типовая переменная, либо S имеет вид X<:U
1
.S
2
, причем
Γ, X<:U
1
S
2
<: T
2
.
Доказательство: Пункт (1) доказывается простой индукцией по деревьям вывода наследования.
Единственный интересный вариант — правило S-Trans, где предположение индукции надо приме-
нить два раза, сначала к правой предпосылке, а затем к левой. Доказательства остальных пунктов
строятся так же, с использованием пункта (1) в варианте с правилом транзитивности.
Упражнение 26.4.11 Рекомендуется, : Докажите следующие «свойства обращения слева на-
право»:
1. Если Γ S
1
S
2
<: T, то либо T Top, либо T T
1
T
2
, причем Γ T
1
<: S
1
и Γ S
2
<: T
2
.
2. Если Γ X<:U.S
2
<: T, то либо T Top, либо T X<:U.T
2
, причем Γ, X<:U S
2
<: T
2
.
3. Если Γ X <: T, то либо T Top, либо T X, либо Γ S <: T при X<:S Γ.
4. Если Γ Top <: T, то T Top.
Лемма 26.4.10, в свою очередь, используется при доказательстве следующего несложного структур-
ного свойства отношения типизации, которое требуется в самых существенных вариантах при доказа-
тельстве свойства сохранения.
Лемма 26.4.12 1. Если Γ λx:S
1
.s
2
: T и Γ T <: U
1
U
2
, то Γ U
1
<: S
1
и существует
некоторый тип S
2
, такой, что Γ, x:S
1
s
2
: S
2
и Γ S
2
<: U
2
.
2. Если Γ λX<:S
1
.s
2
: T и Γ T <: X<:U
1
.U
2
, то U
1
S
1
и существует некоторый тип S
2
,
такой, что Γ, X<:S
1
s
2
: S
2
и Γ, X<:S
1
S
2
<: U
2
.
Доказательство: Прямолинейная индукция по деревьям вывода типов, с использованием Лем-
мы 26.4.10 при шаге индукции (вариант с правилом T-Sub).
После того, как все вспомогательные утверждения установлены, доказательство сохранения типов
не представляет труда.
rev. 104
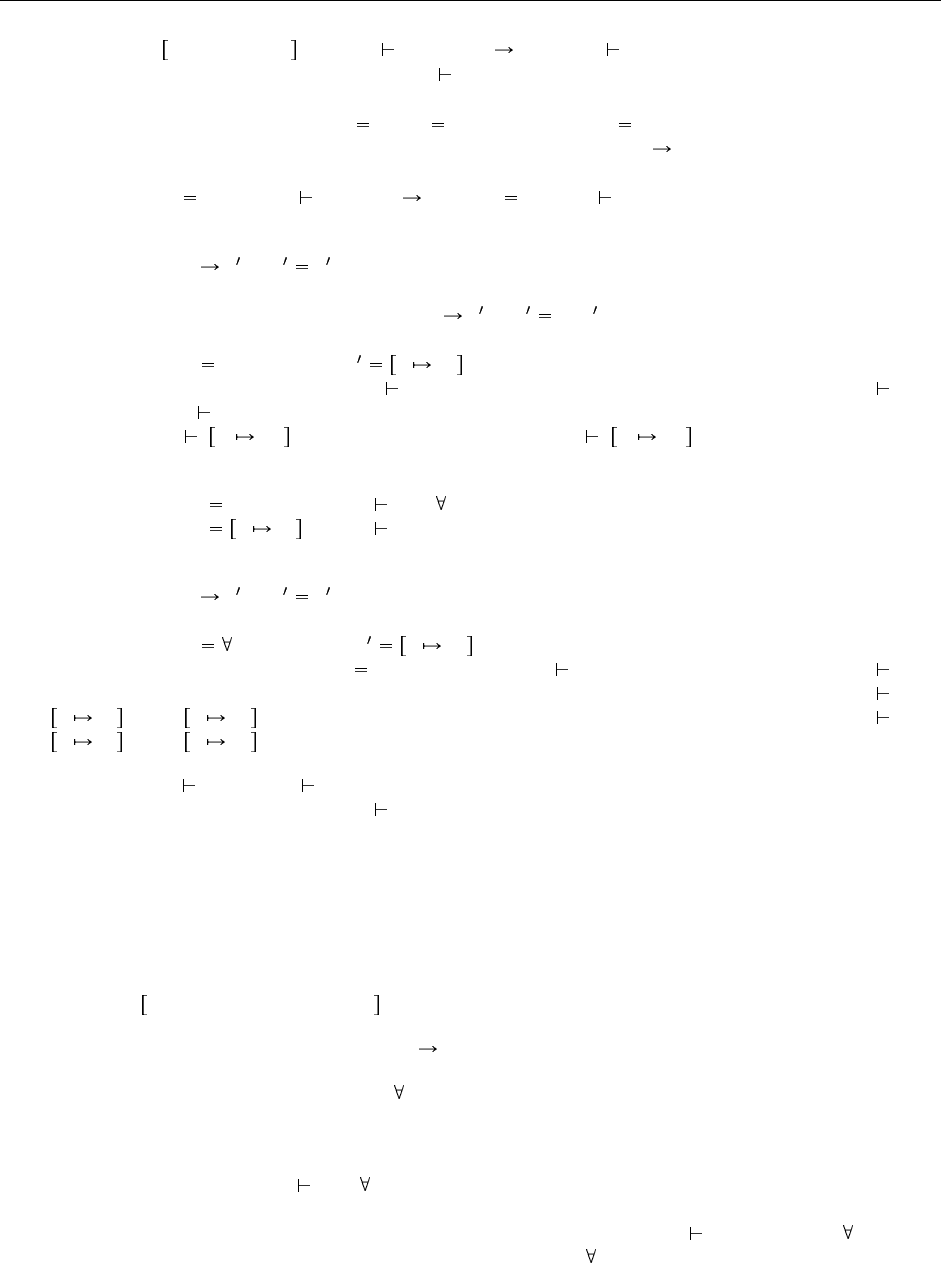
312 26.4. Безопасность
Теорема 26.4.13 Сохранение : Если Γ t : T и t t’, то Γ t’ : T.
Доказательство: Индукция по дереву вывода Γ t : T. При наличии вспомогательных лемм ни один
вариант не представляет особой сложности.
Варианты T-Var, T-Abs, T-TAbs: t x t λx:T
1
.t
2
или t λX<:U.t
2
Эти варианты возникнуть не могут, поскольку мы предполижили t t’, а правил вычисления для
переменных, абстракций и абстракций типа не существует.
Вариант T-App: t t
1
t
2
Γ t
1
: T
11
T
12
T T
12
Γ t
2
: T
11
Исходя из определения отношения вычисления, имеется три подварианта:
Подвариант: t
1
t
1
t t
1
t
2
Результат следует из предположения индукции и правила T-App.
Подвариант: t
1
является значением t
2
t
2
t t
1
t
2
Аналогично.
Подвариант: t
1
λx:U
11
.u
12
t x t
2
u
12
Согласно Лемме 26.4.12, Γ, x:U
11
u
12
: U
12
для некоторого U
12
, такого, что Γ
T
11
<: U
11
и Γ U
12
<: T
12
. По лемме о сохранении типизации при подстановке (Лем-
ма 26.4.6), Γ x t
2
u
12
: U
12
, откуда получаем Γ x t
2
u
12
: T
12
по правилу
T-Sub.
Вариант T-TApp: t t
1
[T
2
] Γ t : X<:T
11
.T
12
T X T
2
T
12
Γ T
2
<: T
11
Исходя из определения отношения вычисления, имеется два подварианта:
Подвариант: t
1
t
1
t t
1
[T
2
]
Результат следует из предположения индукции и правила T-TApp.
Подвариант: t
1
X<:U
11
.u
12
t X T
2
u
12
Согласно Лемме 26.4.12, U
11
T
11
и Γ, X<:U
11
u
12
: U
12
, причем Γ, X<:U
11
U
12
<: T
12
. По свойству сохранения типизации при подстановке (Лемма 26.4.9), Γ
X T
2
u
12
: X T
2
U
12
, откуда по Лемме 26.4.8 и правилу T-Sub имеем Γ
X T
2
u
12
: X T
2
T
12
.
Вариант T-Sub: Γ t : S Γ S <: T
Согласно предположению индукции, Γ t’ : S, и требуемый результат получается по правилу
T-Sub.
Теорема о продвижении для F
<:
является прямолинейным расширением такой же теоремы для про-
стого типизированного лямбда-исчисления с наследованием. Как всегда, вначале мы выписываем лемму
о канонических формах, которая говорит, какой вид могут иметь замкнутые значения функциональных
и квантифицированных типов.
Лемма 26.4.14 Канонические формы :
1. Если v — замкнутое значение типа T
1
T
2
, то v имеет вид λx:S
1
.t
2
.
2. Если v — замкнутое значение типа X<:T
1
.T
2
, то v имеет вид λX<:T
1
.t
2
.
Доказательство: В обоих пунктах проводится индукция по деревьям вывода типов; мы приводим
доказательство только для второй части. При рассмотрении правил типизации становится ясным,
что последнее правило в выводе v : X<:T
1
.T
2
может быть только T-TAbs или T-Sub. Если это
T-TAbs, то требуемый результат немедленно следует из предпосылки правила. Предположим тогда,
что последнее правило T-Sub. Из предпосылок этого правила мы имеем v : S и S <: X<:T
1
.T
2
.
Из леммы об обращении (26.4.10) мы знаем, что S имеет вид X<:T
1
.S
2
. Теперь результат следует
из предположения индукции.
При наличии этой леммы доказательство свойства продвижения не представляет труда.
rev. 104

26.5. Ограниченные экзистенциальные типы 313
<: Top Расширяет F
<:
(26.1) и неограниченную экзистенциальную квантификацию (24.1)
Новые синтаксические формы
T ::= . . . типы:
{ X <:T ,T} экзистенциальный тип
Новые правила наследования Γ S <: T
Γ, X<:U S
2
<: T
2
Γ { X<:U,S
2
} <: { X<:U,T
2
}
(S-Some)
Новые правила типизации Γ t : T
Γ t
2
: X U T
2
Γ U <: T
1
Γ {*U,t
2
} as { X <:T
1
,T
2
} : { X <:T
1
,T
2
}
(T-Pack)
Γ t
1
: { X
<:T
11
,T
12
} Γ, X <:T
11
, x:T
12
t
2
: T
2
Γ let {X,x}=t
1
in t
2
: T
2
(T-Unpack)
Рис. 26.3. Ограниченные кванторы существования (ядерный вариант)
Теорема 26.4.15 Продвижение Если имеется замкнутый правильно типизированный F
<:
-терм t,
то либо t является значением, либо существует некоторый терм t’ такой, что t t’.
Доказательство: Индукция по деревьям вывода типов. Вариант с переменной возникнуть не мо-
жет, поскольку терм t замкнут. Два варианта с лямбда-аюстракциями следуют непосредственно,
поскольку абстракции термов и типов являются значениеми. Варианты с применением, примене-
нием типов и включением более интересны; мы демонстрируем только два последних (применение
термов подобно применению типов).
Вариант T-TApp: t t
1
[T
2
] t
1
: X<:T
11
.T
12
Γ T
2
<: T
11
T X T
2
T
12
Согласно предположению индукции, либо терм t
1
является значением, либо он способен произвести
шаг вычисления. Если он может сделать шаг, то к t применимо правило T-TApp. В противном
случае, если t
1
— значение, то из пункта (2) леммы о канонических формах (26.4.14) нам известно,
что t
1
имеет вид X<:T
11
.t
12
, так что к t оказывается применимо правило E-TAppTAbs.
Вариант T-Sub: Γ t : S Γ S <: T
Результат напрямую следует из предположения индукции.
Упражнение 26.4.16 : Адаптируйте доказательство из этого раздела к полной F
<:
.
26.5. Ограниченные экзистенциальные типы
К экзистенциальным типам (Глава 24) можно добавить ограничения точно так же, как мы это сде-
лали для универсальных типов. При этом получаются ограниченные экзистенциальные типы, изобра-
женные на Рис. 26.3. Как и в случае с ограниченными универсальными типами, правило наследования
S-Some имеет две разновидности — в одной границы сравниваемых кванторов обязаны быть одинако-
выми, во второй им разрешено отличаться.
Упражнение 26.5.1 : Как выглядит полный вариант правила S-Some?
Упражнение 26.5.2 : В чистой Системе F с записями и экзистенциальными типами (но без на-
следования), сколько Вы можете найти способов выбрать T так, чтобы
{* Nat , {a =5 , b =7}} as T;
был правильно типизирован? Если мы добавляем наследование и ограниченные экзистенциальные ти-
пы, появляются ли новые варианты?
В §24.2.1 мы видели, как с помощью обыкновенных экзистенциальных типов можно реализовать аб-
страктные типы данных. Когда мы добавляем ограничения к кванторам существования, этот прирост
выразительности отражается на уровне АТД. Карделли и Вегнер (Cardelli and Wegner 1985) назвали
такие конструкции частично абстрактными типами. Интуитивная идея здесь состоит в том, что огра-
ниченный квантор существования сообщает внешнему миру часть информации о типе представления,
но точное устройство типа представления остается неизвестным.
rev. 104

314 26.5. Ограниченные экзистенциальные типы
Например, предположим, что мы реализовали АТД счетчиков, как в §24.2, но добавили в аннотацию
типа ограничение Counter<:Nat.
coun t e r A D T =
{* Nat , { new = 1, get = λi: Nat . i , inc = λi : Nat . succ ( i )}}
as { Counter <: Nat ,
{ new : Counter , get : Counter - >Nat , inc : Counter - > C ounter }};
coun t e r A D T : { Counter <: Nat ,
{ new : Counter , get : Counter - >Nat , inc : Counter - > C ounter }}
АТД счетчиков может использоваться в точности как раньше, путем связывания его типовой и термовой
компонент переменными Counter и counter и последующего обращения к полям counter для доступа
к операциям над счетчиками
let { Counter , cou nter } = counte r A D T in
co unter . get ( coun ter . inc ( c ounter . inc coun ter . new ));
3 : Nat
Более того, теперь нам разрешается использовать значения Counter напрямую как числа:
let { Counter , cou nter } = counte r A D T in
succ ( succ ( counter . inc count er . new ));
4 : Nat
С другой стороны, мы по-прежднему не имеем права использовать числа как значения типа Counter:
let { Counter , cou nter } = counte r A D T in
co unter . inc 3;
Ошибка: несоответствие типа параметра
В сущности, в этой версии абстракции счетчика мы решили облегчить внешнему миру использование
счетчиков путем открытия внутреннего представления типа; однако мы сохраняем контроль над тем,
как счетчики создаются.
Упражнение 26.5.3 : Предположим, мы хотим определить два абстрактных типа данных,
Counter и ResetCounter, так что (1) оба АТД имеют операции new, get и inc, (2) тип ResetCounter
в дополнение предоставляет операцию reset, принимающую счетчик и возвращающую новый счет-
чик, установленный в какое-то заранее фиксированное состояние, например, 1, (3) клиентам обоих
АТД разрешено использовать ResetCounter вместо Counter (т. е., выполняется ResetCounter <:
Counter), и (4) больше клиентам не дается никакой информации о том, как внутри представлениы
счетчики и счетчики со сбросом. Можно ли выполнить все эти условия при помощи ограниченных
экзистенциальных пакетов?
Можно подобным образом адаптировать и наш способ кодирования объектов на основе экзистенци-
альных типов из §24.2.2. При таком кодировании типы-свидетели экзистенциальных пакетов использо-
вались для представления типов внутреннего состояния объектов, и это состояние всегда было записью,
состоящей из переменных экземпляра. Заменив неограниченный экзистенциальный тип ограниченным,
мы можем показать внешнему миру имена и типы некоторых, но не всех переменных экземпляра объек-
та. Вот, например, объект-счетчик с частично видимым внутренним состоянием, показывающий только
поле x, но ограничивающий доступ к (не слишком интересному) полю private:
c = {*{ x: Nat , pr ivate : Bool } ,
{ state = {x =5 , private = false } ,
me thods = { get = λs :{ x : Nat }. s.x ,
inc = λs :{ x:Nat , p rivate : Bool }.
{x= succ (s. x ), private =s. privat e }}}}
as { X <:{ x : Nat }, { state :X , methods : { get :X - >Nat , inc :X ->X }}};
c : { X <:{ x: Nat }, { state :X , metho ds : { get :X -> Nat , inc :X -> X }}}
rev. 104

26.6. Дополнительные замечания 315
Как и в случае с частично абстрактным АТД счетчиков, наш счетчик-объект позволяет обращаться к
своему значению как через вызов метода get, так и напрямую путем чтения поля x в его состоянии.
Упражнение 26.5.4 : Покажите, как расширить кодирование экзистенциальных типов универ-
сальными из §24.3 на случай кодирования ограниченных экзистенциальных типов через ограниченные
универсальные. Убедитесь, что правило наследования S-Some следует из кодирования и правил на-
следования для ограниченных кванторов.
26.6. Дополнительные замечания
CLU (Liskov et al. 1977 1981; Schaffert 1978; Scheifler 1978) был, судя по всему, первым языком с
безопасной ограниченной квантификацией. Понятие границ параметров в CLU по существу представ-
ляет собой квантификацию — ограниченную квантификацию (§26.2), обобщенную до множественных
параметров-типов.
В форме, рассматриваемой в этой книге, идея ограниченной квантификации была впервые введена
Карделли и Вегнером в языке Fun (Cardelli and Wegner 1985). Их исчисление «ядерный Fun» соответ-
ствует нашей системе F
<:
. Fun был основан на более ранних идеях Карделли, формализован при помощи
методов, разработанных Митчеллом (Mitchell 1984b), и сочетал полиморфизм по Жирару-Рейнольдсу
(Girard 1972; Reynolds 1974) с исчислением наследования первого порядка Карделли (Cardelli 1984).
Исходная версия Fun была упрощена и подверглась некоторому обобщению в работе Брюса и Лонго
(Bruce and Longo 1990), а затем в работе Куриена и Гелли (Curien and Ghelli 1992). В результате полу-
чилось исчисление, которое мы называем полной F
<:
. Наиболее подробным обзором по ограниченной
кватификации является статья Карделли, Мартини, Митчелла и Щедрова (Cardelli, Martini, Mitchell
and Scedrov 1994).
F
<:
и родственные системы активно изучались теоретиками и разработчиками языков программиро-
вания. Первые примеры ограниченной квантификации были даны в статье-обзоре Карделли и Вегнера;
дальнейшие примеры последовали в работе Карделли по степенным видам (Cardelli 1988a). Куриен и
Гелли (Curien and Ghelli 1992; Ghelli 1990) рассматривают некоторые синтаксические свойства F
<:
. Се-
мантические свойства систем, близких к F
<:
, изучаются в работах Брюса и Логно (Bruce and Longo
1990), Мартини (Martini 1988), Бреазу-Таннена, Кокана, Гантера и Щедрова (Breazu-Tannen, Coquand,
Gunter and Scedrov 1991), Кардоне (Cardone 1989), Карделли и Лонго (Cardelli and Longo 1991), Кар-
делли, Мартини, Митчелла и Щедрова (Cardelli, Martini, Mitchell and Scedrov 1994), Куриена и Гелли
(Curien and Ghelli 1992, 1991) и Брюса и Митчелла (Bruce and Mitchell 1992).
Карделли и Митчелл (Cardelli and Mitchell 1991), Брюс (Bruce 1991), Карделли (Cardelli 1991), а
также Кэннинг, Кук, Хилл, Олтхофф и Митчелл (Canning, Cook, Hill, Olthoff and Mitchell 1989b) расши-
рили F
<:
, добавив типы-записи и более богатое понятие наследования. Ограниченная квантификация
играет ключевую роль в языке Quest, созданном Карделли (Cardelli 1991; Cardelli and Longo 1991), в
языке Abel, разработанном в лабораториях HP (Canning, Cook, Hill and Olthoff 1989a; Canning, Cook,
Hill, Olthoff and Mitchell 1989b; Canning, Hill and Olthoff 1988; Cook, Hill and Canning 1990), и в недавних
разработках вроде GJ (Bracha, Odersky, Stoutamire and Wadler 1998), Pict (Pierce and Turner 2000) и
Funnel (Odersky 2000).
Воздействие ограниченной квантификации на кодирование по Чёрчу (§26.3) рассматривалось у Гел-
ли (Ghelli 1990), а также Карделли, Мартини, Митчеллом и Щедровым (Cardelli, Martini, Mitchell and
Scedrov).
Расгирение F
<:
типами-пересечениями (15.7) исследовалось Пирсом (Pierce 1991b, 1997b). Вариант
той же системы с видами высшего порядка применяется к моделированию объектно-ориентированных
языков с множественным наследованием в работе Компаньони и Пирса (Compagnoni and Pierce 1996);
метатеоретические свойства таких языков анализирует Компаньони (Compagnoni 1994).
rev. 104

316 26.6. Дополнительные замечания
rev. 104

Глава 27
Расширенный пример: еще раз
императивные объекты
В Главе 18 мы разработали набор идиом на языке простого типизированного исчисления с запи-
сями, ссылками и наследованием, моделирующих основные черты и приемы императивного объектно-
ориентированного стиля программирования. В конце этой главы (§18.12) мы предприняли некоторые
усилия, чтобы повысить эффективность наших объектов. Для этого мы перенесли действия по постро-
ению таблицы методов объекта с времени вызова метода на время создания объекта. В этой главе мы
с помощью ограниченной квантификации проводим дальнейшие улучшения в эффективности нашей
модели.
Основной идеей §18.12 было передавать классу при вызове ссылку на «таблицу методов self». Класс
использует эту ссылку при определении своих методов, а затем мы подправляем ссылку так, чтобы
она указывала на заполненную таблицу методов, возвращенную классом. Например, если SetCounter
и SetCounterRep являются публичным интерфейсом и типом внутреннего представления для класса
объектов-счетчиков с методами get, set и inc,
SetC o u n t e r = { get :Unit - > Nat , set : Nat -> Unit , inc : Unit -> Unit };
Coun t e r R e p = {x : Ref Nat };
то мы можем реализовать класс счетчиков с присваиванием так:
setCounterClas s =
λr : Co u n t erRep . λself : Source SetC o u n t er .
{ get = λ_: Unit . !( r.x ) ,
set = λi : Nat . r.x :=i ,
Примерами в этой главе служат термы F
<:
с записями (Рис. 15.3) и ссылками (13.1). Соответствующий интерпретатор
на OCaml называется fullfsubref.
В списке ошибок и опечаток на сайте книги (http://www.cis.upenn.edu/~bcpierce/tapl/errata.txt) приводятся сле-
дующие соображения:
Глава 27 в целом не слишком убедительна. Цель использования F
<:
, вроде бы, состоит в том, чтобы
создавать таблицу методов один раз для каждого класса, а не для каждого объекта. Код, действительно,
создает нечто по одному разу для каждого класса, однако это нечто является функцией, которая создает
таблицу методов при каждом открытом рекурсивном вызове через self ! (См. вызовы (!self r), которые
происходят при обращении к методам.) Другими словами, эффективность в итоге оказывается хуже, чем
та, что мы получили в конце Главы 18.
Я благодарен Джону Тангу Бойланду, указавшему на это обстоятельство. Джон также предлагает другой
расширенный пример, использующий F
<:
в стиле Главы 32 для реализации объектов в императивном стиле.
Набросок основной конструкции можно найти здесь:
http://www.cis.upenn.edu/~bcpierce/tapl/boyland-object -encoding.txt
Код, реализующий эту идею, находится по адресам
http://www.cs.uwm.edu/classes/cs790/types-f2003/Chapte r27-replacement.txt
http://www.cs.uwm.edu/classes/cs790/types-f2003/fullfo msubref.tar.gz
— прим. перев.
317
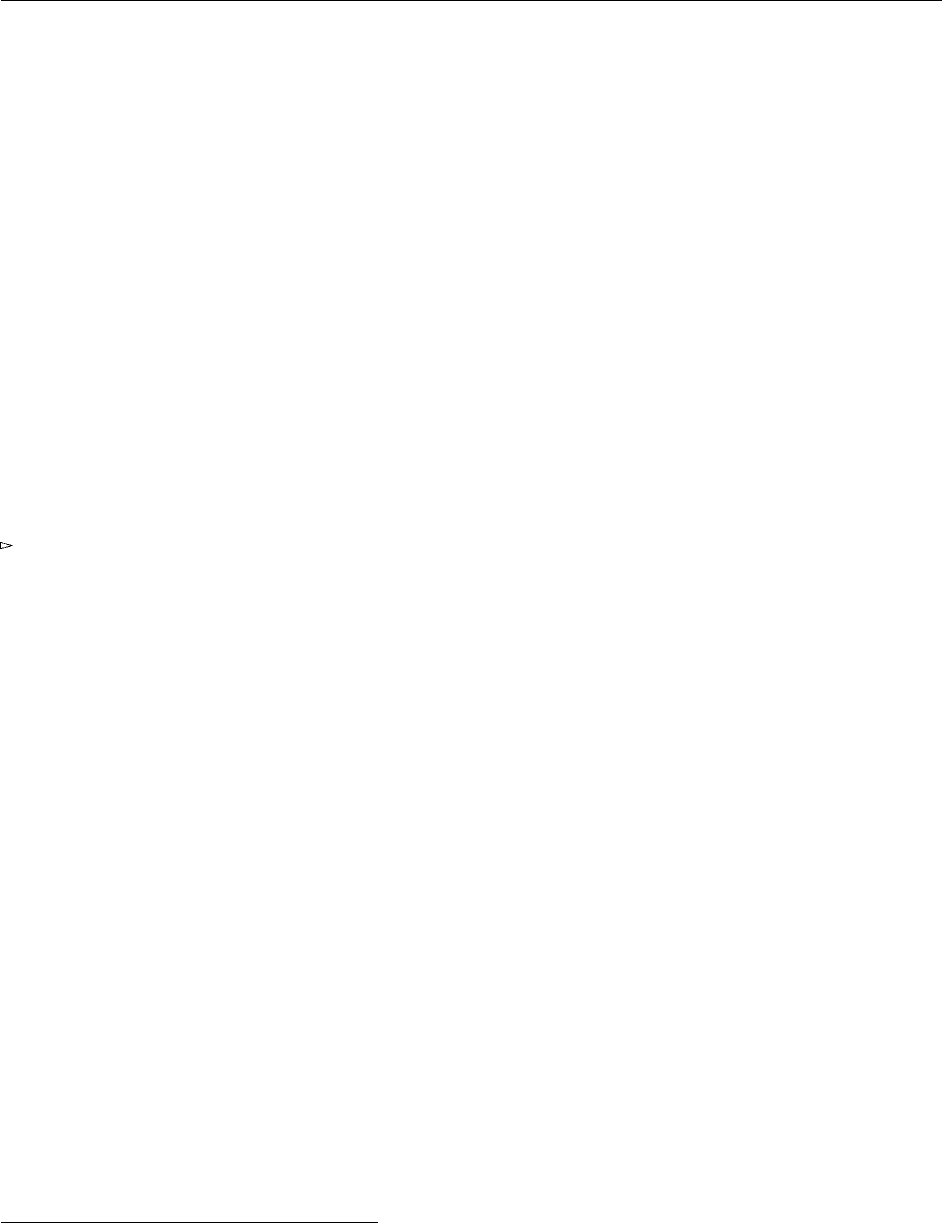
318
inc = λ_ : Unit . (! self ). set
( succ ((! self ). get unit ))};
Для параметра self мы используем тип Source SetCounter, а не Ref SetCounter, потому что, когда
мы определяем подкласс SetCounterClass, self этого нового класса будет иметь другой тип. Например,
если InstrCounter и InstrCounterRep — типы интерфейса и представления класса объектов-счетчиков
с подсчетом доступа
instrCounter = { get : Unit - >Nat , set : Nat -> Unit ,
inc :Unit - > Unit , access e s : Unit - > Nat };
InstrCounterRe p = { x : Ref Nat , a: Ref Nat };
то сам класс можно определить так:
instrCoun t e r C l as s =
λr : InstrCounterRep . λself : Source InstrCounter .
let super = se tC o u n t e r Cl a s s r self in
{ get = super . get ,
set = λi : Nat . (r. a := succ (!( r.a )); super . set i) ,
inc = super . inc ,
acc esses = λ_; Unit .
!( r.a )};
instrCoun t e r C l as s : I n s t rC o u n t e r R ep ->
( So urce InstrCounter ) -> InstrCounter
Типом параметра self здесь будет Source InstrCounter, и нам нужно иметь возможность преобразо-
вать Source InstrCounter в Source SetCounter, чтобы передать этот self как аргумент self класса
setCounterClass при построении super. Ковариантный конструктор Source позволяет такое преобра-
зование, в то время как с инвариантным конструктором Ref оно было бы запрещено.
Однако, как мы заметили в конце §18.12, эффективность этой модели классов по-прежнему не
оптимальна. Поскольку таблицы, связанные с каждым объектом, порожденным определенным классом,
одинаковы, должно быть возможно построить такую таблицу всего один раз, во время создания класса,
и использовать ее каждый раз при создании объекта. При этом более точно окажутся смоделированы
соглашения по реализации настоящих объектно-ориентированных языков, где объект не несет при себе
никаких методов, а только указатель на структуру данных, представляющую его класс, и именно в
этой структуре хранятся сами объекты.
1
Еще один способ сказать то же самое — заметить, что порядок параметров в вышеприведенных
классах (сначала переменные экземпляра, потом self) неверный: параметр self требуется для постро-
ения таблицы класса, а запись переменных экземпляра r используется только тогда, когда у готового
объекта зовутся методы. Если бы self был первым аргументом, мы могли бы вычислять таблицу ме-
тодов прежде, чем нам передадут аргумент r; можно было бы сначала один раз частично применить
класс к его аргументу self, проделать это вычисление раз и навсегда, и сделать множество копий
получившейся таблицы методов, применяя ее ко многим записям переменных экземпляра. Конкретно,
нам хотелось бы переписать setCounterClass так:
setCounterClas s =
λself : So urce ( CounterRep -> SetCounter ).
λr : Co u n t erRep .
{ get = λ_: Unit , !( r. x ),
set = λi : Nat , r.x :=i ,
inc = λ_ : Unit . (! self .r ). set
( succ ((! self r ). get unit ))};
1
На самом деле настоящие объектно-ориентированные языки идут еще дальше. Вместо того, чтобы вычислять и
хранить полную таблицу методов, каждый класс хранит только те методы, которые в нем добавлены или переопределены
по сравнению с надклассом. Так что таблица методов в нашем понимании вообще не строится — при вызове метода мы
просто проходим вверх по иерархии классов, начиная с класса объекта-адресата, пока не найдется определение нужного
нам метода. Такой поиск во время выполнения создает нетривиальные проблемы для статического анализа типов, но
здесь мы их касаться не будем.
rev. 104
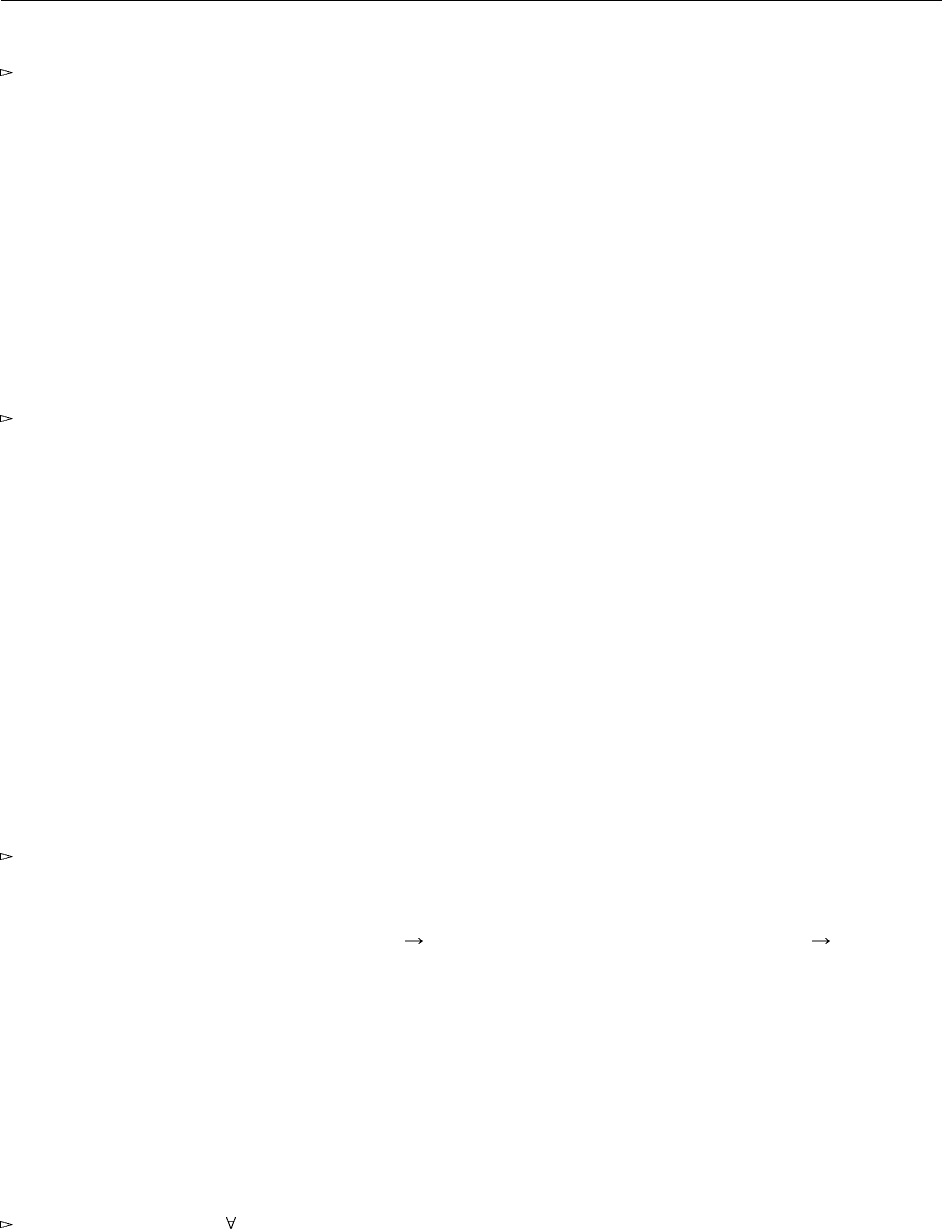
319
setCounterClas s : ( S ource ( Cou nterRep - > Se t C o unter )) ->
Coun t e r R e p -> SetCounter
Между этой версией и предыдущей есть три существенных отличия. Во-первых, новая вер-
сия принимает сначала self, а уже потом r. Во-вторых, тип self поменялся с SetCounter на
CounterRep->SetCounter. Это второе изменение вызвано первым, поскольку тип self должен быть
такой же, как тип таблицы методов, возвращаемой классом. И в-третьих, все вызовы !self в теле
класса превращаются в (!self r). Это третье изменение вызвано вторым.
Функция порождения объекта для наших счетчиков определена так:
newSetCounter =
let m = ref (λr : C o u n t erRep . error as Set C o u nter ) in
let m ’ = s e t C o u n te r C l a s s m in
(m := m ’;
λ_ : Unit . let r = {x= ref } in m ’ r );
newSetCounter : Unit -> S e t Counter
Заметим, что первые три строки в этом определении вычисляются только один раз, когда определя-
ется newSetCounter. Вычисление останавливается, дойдя до элементарной абстракции на последней
строке, и эту строку можно применить сколько угодно раз при создании объектов; каждый раз будет
выделяться участок памяти для новой записи переменных экземпляра r, и таблица методов m’ будет
устанавливаться в указатель на r. В результате получается свежий объект.
К сожалению, переупорядочив таким образом setCounterClass, мы ввели в тип состояния контра-
вариантное вхождение типа-состояния CounterRep. Это нам аукнется, когда мы попытаемся опреде-
лить подкласс setCounterClass.
instrCoun t e r C l as s =
λself : So urce ( InstrCou n terRep -> I n s t r C o u n ter ).
let super = se tC o u n t e r Cl a s s self in
λr : InstrCounterRep .
{ get = ( super r ). get ,
set = λi : Nat . (r. a := succ (!( r.a )); ( super r ). set i ),
inc = ( super r) inc ,
acc esses = λ_: Unit . !( r.a )};
Ошибка: несоответствие типа параметра
Несоответствие возникает в определении super, когда мы порождаем экземпляр надкласса
setCounterClass с тем же self, который был передан подклассу. К сожалению, текущий self является
ссылкой на функцию типа InstrCounterRep InstrCounter, а это не подтип CounterRep SetCounter,
поскольку наследование с левой стороны стрелок направлено не туда.
С этой трудностью можно справиться, если еще раз переписать setCounterClass, теперь используя
ограниченную квантификацию.
setCounterClas s =
λR <: CounterR e p .
λself : So urce (R -> SetCounter ).
λr : R .
{ get = λ_: Unit . !( r.x ) ,
set = λi : Nat . r.x := i,
inc = λ_ : Unit . (! self .r ). set ( succ ((! self r). get unit ))};
setCounterClas s : R <: C o unterRep .
( So urce (R -> SetCounter )) -> R -> SetCo u n t er
Этим изменением мы добиваемся того, что setCounterClass начинает несколько менее строго относить-
ся к передаваемому в него параметру self. Немного антропоморфизируя, можно представить себе, что
предыдущая версия setCounterClass говорит своему окружению: «Дайте мне, пожалуйста, параметр
rev. 104
320
self, принимающий параметром CounterRep, и я из него сделаю таблицу методов, которая тоже ожи-
дает параметром CounterRep». Новая же версия говорит: «Пожалуйста, скажите мне, какой будет тип
представления R у порождаемого нами объекта; в этом типе должно быть по крайней мере поле x,
поскольку оно мне нужно. Потом дайте мне (ссылку на) self, принимающий R как параметр и возвра-
щающий таблицу методов по крайней мере с интерфейсом SetCounter, а я построю и верну еще один
такой же объект».
Яснее всего эффект такого изменения виден при определении подкласса instrCounterClass.
instrCoun t e r C l as s =
λR <: InstrCou n t e r R e p .
λself : So urce (R -> I n s t r C o u n t e r ).
λr : R .
let super = se tC o u n t e r Cl a s s [ R] self in
{ get = ( super r ). get ,
set = λi : Nat . (r.a := succ (!( r . a )); ( super r ). set i),
inc = ( super r ). inc ,
acc esses = λ_: Unit . !( r.a )};
instrCoun t e r C l as s : R <: InstrCounterR e p .
( So urce (R -> InstrCounter )) ->
R -> InstrCounter
Этот код работает там, где предыдущий вариант ломался, потому, что в выражении, связанном с пере-
менной super, иначе работает правило включения: мы поднимаем тип self и делаем его приемлемым
для надкласса. Раньше мы пытались показать
So urce ( Inst rCounte rRep - > InstrCounter )
<: Sour ce ( CounterRep - > Se t C ounter )
что было неверно. Теперь нам надо показать только
So urce (R -> I n s t r C o u n t e r ) <: Sour ce (R -> SetCou n t e r )
а это истинно.
Функции создания объектов для нашего нового кодирования классов очень похожи на старые вари-
анты. Вот, например, функция создания для подкласса счетчиков с подсчетом доступа.
newInstrCounte r =
let m = ref (λr : InstrCounterRe p . error as InstrCounter ) in
let m ’ = i n s t rC o u n te r C l a ss [ InstrCounterR e p ] m in
(m := m ’;
λ_ : Unit . let r = {x= ref 1 , a = ref 0} in m ’ r );
newInstrCounte r : Unit -> In s t r C o u n t e r
Единственная разница состоит в том, что требуется конкретизировать InstrCounterClass реальным
типом записи переменных экземпляра, InstrCounterRep. Как и раньше, первые три строки вычисля-
ются всего один раз, при связывании переменной newInstrCounter.
Наконец, приведем несколько тестов, показывающих, что наши счетчики работают как полагается:
ic = n e w I n s t r Co u n t e r unit ;
ic . inc unit ;
ic . get unit ;
2 : Nat
ic . ac cesses unit ;
1 : Nat
Упражнение 27.0.1 Рекомендуется : Наше новое кодирование классов опирается на ковари-
антность конструктора типов Source. Можно ли достигнуть такой же эффективности (т. е.,
rev. 104
