Пирс Б. Типы в языках программирования

Подождите немного. Документ загружается.

29.1. Неформальное введение 341

* вид простых типов (скажем, Bool или Bool Bool)

* * вид операторов над типами (т. е, функций, переводящих про-

стые типы в простые типы)

* * * вид функций, переводящих простые типы в операторы над ти-

пами (т. е., вид двуместных операторов)

(* *) * вид функций, переводящих операторы над типами в простые

типы.

Таким образом, виды являются «типами типов». В сущности, система видов представляет собой копию

простого типизированного лямбда-исчисления «уровнем выше».

В дальнейшем мы будем использовать слово тип для любого выражения на уровне типов — т. е.,

как для обыкновенных типов вроде Nat и X.X X, так и для операторов над типами вроде λX.X. Когда

нам будет нужно говорить об обыкновенных типах (т. е., выражениях типа, которые используются при

классификации термов), мы будем называть их простыми типами.

Выражения типа с видами вроде (* *) * называются операторами высших порядков над типами.

В отличие от функций высших порядков на уровне термов, которые часто весьма полезны, оператоы

высших порядков над типами скорее являются экзотикой. Один класс примеров их использования мы

встретим в Главе 32.

Чтобы упростить задачу проверки видов для выражений типа, мы каждую абстракцию на уровне

типов снабжаем указанием на вид ее связанной переменной. Например, официальное определение опе-

ратора Pair таково:

Pair = λA ::*. λB ::*. X . (A ->B ->X ) -> X ;

(обратите внимание на сдвоенное двоеточне.) Однако, поскольку почти все такие аннотации будут иметь

вид *, мы продолжим писать λX. T как сокращение от λX::*. T.

Прояснить картину можно при помощи диаграмм. Выржения нашего языка теперь делятся на три

отдельных класса: термы, типы и виды. На уровне термов мы имеем элементарные значения (целые,

числа с плавающей точкой и т. п.), составные значения (записи и т. п.), абстракции и применения на

уровне значений, абстракции типов и применения типов:

λx:Nat.x

(λx:Nat.x) true

λX.λx:X.x

(λx:Nat.x) 5

pair [Nat] [Bool] 5 false

?> =<

89 :;

Термы

На уровне типов имеется две разновидности выражений. Во-первых, есть простые типы вроде Nat,

Nat Nat, Pair Nat Bool и X.X X, населенные термами. (Разумеется, не у всех термов имеется тип;

например, его нет у (λx:Nat.x) true.)

Nat Pair Nat Bool

(λX.X X) Nat

Nat Nat

X.X X

?> =<

89 :;

Типы

λx:Nat.x

(λx:Nat.x) true

λX.λx:X.x



(λx:Nat.x) 5

VV,

pair [Nat] [Bool] 5 false

YY4

?> =<

89 :;

Термы

Существуют также операторы над типами, вроде Pair и λX.X X, которые сами по себе не служат

для классификации термов (то есть, не имеет смысла вопрос «Какие термы имеют тип λX.X X?»).

Однако они могут быть применены к аргументам, давая при этом простые типы вроде (λX.X X) Nat,

а уже те, в свою очередь, используются при классификации термов.

rev. 104

342 29.1. Неформальное введение

Nat Pair Nat Bool Pair

(λX.X X) Nat

λX.X X

Nat Nat

X.X X

Pair Nat Pair Pair

?> =<

89 :;

Типы

λx:Nat.x

(λx:Nat.x) true

λX.λx:X.x



(λx:Nat.x) 5

VV,

pair [Nat] [Bool] 5 false

YY4

89 :;

Термы

Заметим, что простые типы — т. е., типовые выражения вида *, — могут в качестве синтаксических

составляющих включать операторы высшего порядка над типами, например, (λX.X X) Nat или Pair

Nat Bool. Точно так же термовые выражения, принадлежащие базовым типам вроде Nat, могут в

качестве подвыражений содержать лямбда-абстракции, как, например, (λx:Nat.x) 5.

Наконец, имеется уровень видов. Простейшим видом является *; он содержит в качестве членов

все простые типы.

!"#

Виды

Nat

Pair Nat Bool

Pair

(λX.X X) Nat

ggN

λX.X X

Nat Nat

YY3

X.X X

Pair Nat Pair Pair

?> =<

89 :;

Типы

λx:Nat.x

(λx:Nat.x) true

λX.λx:X.x



(λx:Nat.x) 5

VV,

pair [Nat] [Bool] 5 false

YY4

?> =<

89 :;

Термы

Операторы над типами, скажем, λX.X X или Pair, принадлежат функциональным видам вроде * *

или * * *. Неверно построенные выражения на уровне типов, вроде Pair Pair, ни к какому виду не

принадлежат.

rev. 104

29.1. Неформальное введение 343

* * * * * *

'& %$

! "#

Виды

Nat

Pair Nat Bool

Pair

(λX.X X) Nat

ggN

λX.X X

Nat Nat

YY3

X.X X

Pair Nat

Pair Pair

?> =<

89 :;

Типы

λx:Nat.x

(λx:Nat.x) true

λX.λx:X.x



(λx:Nat.x) 5

VV,

pair [Nat] [Bool] 5 false

YY4

?> =<

89 :;

Термы

Упражнение 29.1.1 : Чем отличаются по значению выражения типового уровня X.X X и

λX.X X?

Упражнение 29.1.2 : Почему функциональный тип вроде Nat Nat не принадлежит функциональ-

ному виду вроде * *?

Теперь разумным кажется вопрос: «Зачем останавливаться на третьем уровне выражений?». Нельзя

ли ввести функции, переводящие виды в виды, применение на уровне видов, и т. п., добавить четвертый

уровень для классфификации видов в соответствии с их функциональным построением, и продолжать

в том же духе до бесконечности? Системы такого рода исследовались в рамках теории систем чистых

типов (Terlouw 1989; Berardi 1988; Barendregt 1991, 1992; Jutting, McKinna and Pllack 1994; McKinna

and Pollack 1993; Pollack 1994). Однако для языков программирования оказалось достаточно иметь три

уровня.

Действительно, при том что операторы над типами в какой-то форме присутствуют во всех статиче-

ски типизированных языках программирования, проектировщики языков редко дают программистам

доступ даже ко всем выразительным возможностям нашей теперешней системы. В некоторых языках

(напр., Java), есть лишь ограниченный набор встроенных операторов вроде Array, и нет возможности

определять новые. В других языках операторы над типами совмещены с другими языковыми конструк-

циями; например, в ML такие операторы включены в механизм datatype. Разрешается определять

параметрические типы данных , такие как

type ’a Tyop = tyopta g of ( ’ a -> a );

что мы бы записали как

Tyop = λX . < tyoptag :X ->X >;

Другими словами, в ML можно определять параметрические варианты, но не произвольные парамет-

рические типы. Это ограничение имеет то преимущество, что каждый раз, когда оператор Tyop встре-

чается на уровне типов, на уровне термов будет присутствовать соответствующий тег tyoptag. Таким

образом, каждое место, где компилятор должен с помощью отношения эквивалентности определений

В этом примере мы игнорируем соглашения ML по использованию больших и малых букв в идентификаторах. На

самом деле, в OCaml это определение записывалось бы как

type ’a tyop = Tyopta g of ( ’ a -> a );

rev. 104

344 29.2. Определения

свести тип вроде Tyop Nat к редуцированной форме Nat Nat, явно помечено в программе благодаря

присутствию tyoptag. Это существенно упрощает алгоритм проверки типов.

Здесь мы рассматриваем только один конструктор видов, . Однако в литературе исследовалось

и множество других; спектр систем видообразования, способных проверять и отслеживать различные

свойства типовых выражений, сравним со спектром систем типов, проверяющих и отслеживающих

свойства термов. Имеются виды записей (их элементами являются записи типов — которые не следует

путать с типами записей; через такие виды естественным образом определяются системы взаимно ре-

курсивных типов), строковые виды (описывающие «строки полей»; с их помощью можно сконструиро-

вать типы записей в системах, поддерживающих полиморфизм через переменные строк — см. стр. 263),

степенные виды, они же степенные типы (через них строится альтернативный подход к наследованию,

см. Cardelli 1988a), одноэлементные виды (связанные с определениями — см. стр. 340, а также с систе-

мами модулей с разделением — см. стр. 356), зависимые виды («высокоуровневый» аналог зависимых

типов, описываемых в §30.5), и многие другие.

29.2. Определения

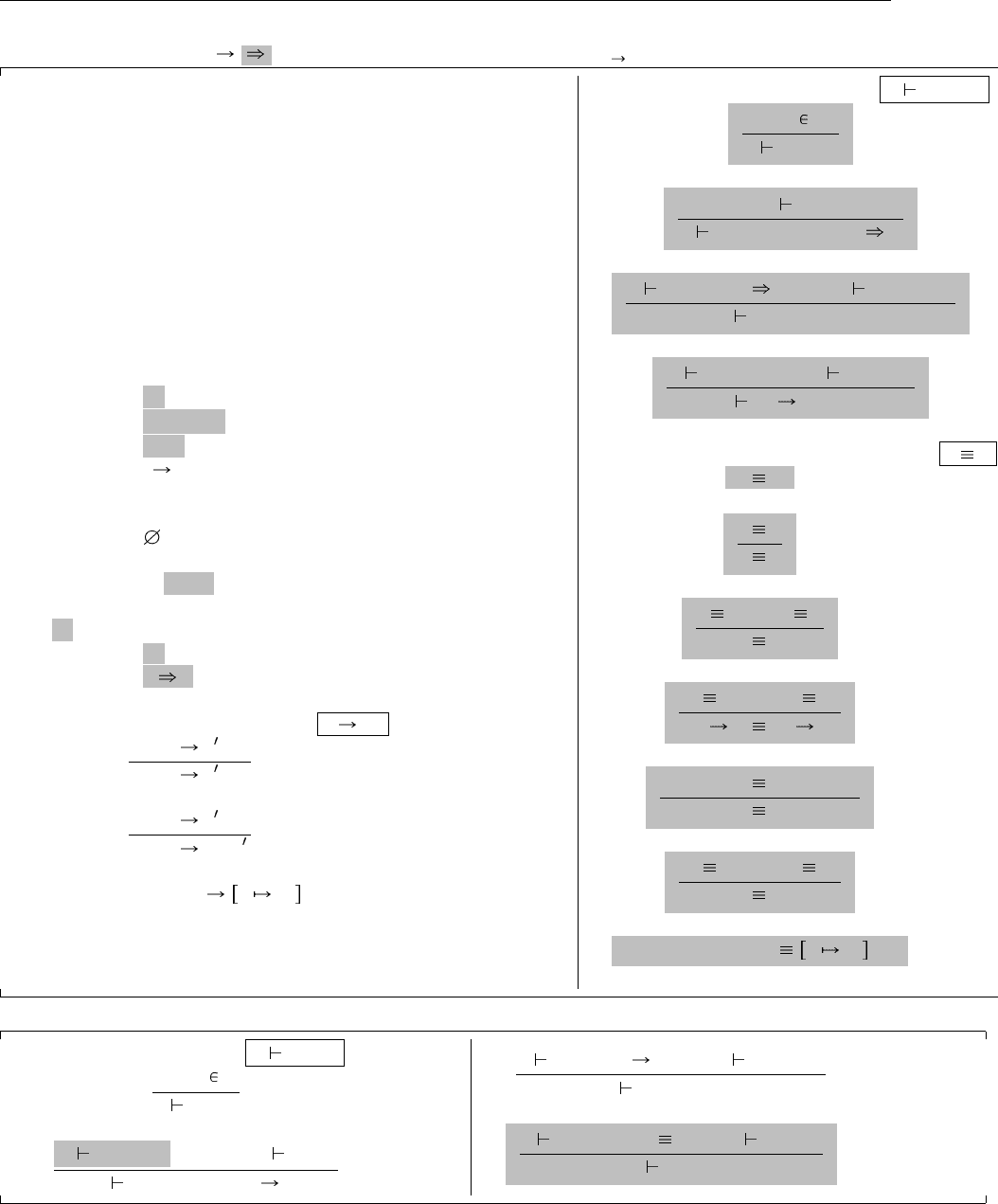
Полное определение базового лямбда-исчисления с операторами над типами приведено на Рис. 29.1.

На уровне термов это исчисление включает только переменные, абстракцию и применение из про-

стого типизированного лямбда-исчисления (и поэтому называется простое типизированное лямбда-

исчисление с операторами над типами). На уровне типов мы имеем обыкновенные функциональные

типы и типовые переменные, а также абстракцию и применение операторов. Кванторные типы вроде

X.T в эту систему не включены; мы подробно их рассмотрим в Главе 30.

Наше представление системы с видами расширяет конструкцию простого типизированного лямбда-

исчисления в трех отношениях. Во-первых, вводится набор правил присвоения видов, указывающих,

как можно сочетать выражения типа и получать при этом новые выражения типа. Запись Γ T :: K

означает «тип T принадлежит виду K в контексте Γ». Обратите внимание на сходство этих правил с

правилами типизации для исходного простого типизированного лямбда-исчисления (Рис. 9.1).

Во-вторых, каждый раз, когда внутри терма встречается тип T (в форме λx:T.t), требуется прове-

рить, правильно ли T образован. Поэтому к старому правилу T-Abs добавляется новая предпосылка,

Γ T :: *. Заметим, что T должен иметь в точности вид * — т. е., это должен быть простой тип, —

поскольку он используется для характеристики значений, которые разрешено принимать переменной

x. Правила типизации соблюдают инвариант, что всякий раз, когда мы можем вывести утверждение

Γ t : T, выводимо будет и утверждение Γ T :: (при условии, что все упоминаемые в контексте

типы имеют правильные виды). Этот момент подробнее обсуждается в §30.3.

В-третьих, добавляется набор правил, касающихся отношения эквивалентности определений меж-

ду типами. Мы пишем S T, что читается «определения типов S и T эквивалентны». Это отношение

весьма похоже на отношение редукции на уровне термов. Влияние эквивалентности определений на

типизацию отражено в новом правиле T-Eq. Предпосылка о видах (опущенная в предыдущем разделе,

где мы обсуждали это правило) поддерживает вышеупомянутый инвариант, «термы с правильными

типами всегда имеют типы с правильными видами». Заметим, что это правило похоже на правило

включения (T-Sub) в системах с наследованием.

Для доказательства основных метатеоретических свойств этой системы требуется некоторая работа,

поскольку отношение эквивалентности между типами ведет к немалой гибкости в «формах» типов,

присваиваемых термам. Мы откладываем исследование этой теории до Главы 30.

Это ограничение подобно тому, как в ML обрабатываются рекурсивные типы (см. §20.1). Объединение рекурсивных

типов с определениями datatype дает программисту удобство эквирекурсивных типов, а компилятору простоту изоре-

курсивных, поскольку аннотации fold/unfold упрятываются в операции пометки и разбора случаев, необходимые при

работе с вариантными типами.

rev. 104

29.2. Определения 345

Расширяет λ (9.1)

Синтаксис

t ::= термы:

x переменная

λx:T.t абстракция

t t применение

v ::= значения:

λx:T.t значение-абстракция

T ::= типы:

X типовая переменная

λX::K.T абстракция оператора

T T применение оператора

T T тип функций

Γ ::= контексты:

пустой контекст

Γ, x:T связывание термовой переменной

Γ, X::K связывание типовой переменной

K ::= виды:

* вид простых типов

K K вид операторов

Вычисление t t’

(E-App1)

(E-App2)

(λ x:T

) v

x v

(E-AppAbs)

Присвоение видов Γ T :: K

X::K Γ

Γ X :: K

(K-TVar)

Γ, X::K

:: K

Γ λX::K

:: K

(K-Abs)

Γ T

:: K

Γ T

:: K

Γ T

:: K

(K-App)

Γ T

:: * Γ T

:: *

Γ T

:: *

(K-Arrow)

Эквивалентность типов S T

T T (Q-Refl)

T S

S T

(Q-Symm)

S U U T

S T

(Q-Trans)

(Q-Arrow)

λX::K

(Q-Abs)

(Q-App)

(λX::K

) T

X T

(Q-AppAbs)

см. на след. странице. . .

Типизация Γ t : T

x : T Γ

Γ x : T

(T-Var)

Γ T

:: * Γ, x:T

Γ λx:T

: T

(T-Abs)

Γ t

: T

Γ t

: T

Γ t

: T

(T-App)

Γ t : S S T Γ T :: *

Γ t : T

(T-Eq)

Рис. 29.1. Операторы над типами и виды (λ

)

rev. 104

346 29.2. Определения

rev. 104

Глава 30

Полиморфизм высших порядков

После того, как в Главе 29 мы добавили к λ операторы над типами, естественным следующим

шагом будет сочетать их с другими типовыми конструкциями, изученными нами на протяхении этой

книги. В этой главе мы добавляем операторы над типами к полиморфизму Системы F и получаем

широко известную систему, называемую F

(Girard 1972). В Главе 31 исчисление обогащается насле-

дованием, и получается Система F

. Эта последняя служит основой нашего последнего расширенного

примера с чисто функциональными объектами в Главе 32.

Определение F

строится как простое сочетание черт λ

и Системы F. Однако доказательство

основных свойств этой системы (в частности, сохранения и продвижения) требует больше усилий, чем

в большинстве виденных нами систем, поскольку приходится учитывать, что проверка типов требует

вычислений на уровне типов. Построение этих доазательств и является основной задачей данной главы.

30.1. Определения

Система F

получается при сочетании Системы F из Главы 23 и λ

из Главы 29, с добавлением анно-

таций вида (X::K) всюду, где связываются типовые переменные (т. е., в абстракциях типа и кванторах).

Формальное определение системы, содержащей только кванторы всеобщности (но не существования)

дано на Рис. 30.1. Мы приводим все правила полностью, чтобы облегчить чтение доказательств в §30.3,

несмотря на то, что отличия от предыдущих систем минимальны.

Мы сокращаем X::*.T как X.T, а { X::*,T} как { X,T}, так что термы Системы F могут напря-

мую рассматриваться в качестве термов F

Подобным образом можно получить экзистенциальные типы высших порядков путем обобщения X

до X::K в исходном представлении кванторов существования из Главы 24. Это расширение приведено

на Рис. 30.2.

30.2. Пример

Расширенный пример программирования с использованием абстракций, включающих операторы

над типами, мы увидим в Главе 32. Здесь мы рассмотрим намного более скромный пример.

Вспомним кодирование абстрактных типов данных при помощи экзистенциальных типов из §24.2.

Теперь допустим, что мы хотим реализовать АТД пар, точно так же, как раньше мы реализовывали

АТД таких типов, как счетчики. Наш новый АТД должен предоставлять операции для построения пар

и для доступа к их элементам. Более того, хотелось бы, чтобы эти операции были полиморфны, так,

чтобы с их помощью можно было строить и использовать пары элементов любых типов S и T. Таким

образом, предоставляемый нами абстрактный тип не должен быть простым типом, а должен являться

абстрактным конструктором типа (или оператором над типами). Он должен быть абстрактным в

Примеры из этой главы являются термами F

(Рис. 30.1) с записями, булевскими значениями и кванторами суще-

ствования (30.2). Соответствующий интерпретатор на OCaml называется fullomega. Для зависимых типов, упоминаемых

в §30.5, реализация отсутствует.

347

348 30.3. Свойства исчисления

том же смысле, в каком абстрактными были АТД, с которыми мы работали раньше: для каждых S и

T, операция pair должна брать элемент S и элемент T и возвращать элемент Pair S T, а fst и snd

должны принимать элемент Pair S T, а возвращать, соответственно, элемент S или T, и этим должны

ограничиваться сведения, известные клиенту нашей абстракции.

Исходя из этих требований, нетрудно построить сигнатуру, которую наш АТД пар должен демон-

стрировать миру:

Pa irSig = { Pair ::* * *.

{ pair : X . Y . X - >Y - >( Pair X Y) ,

fst : X . Y . ( Pair X Y )- >X ,

snd : X . Y . ( Pair X Y )- >Y }};

То есть, реализация пар должна предоставлять оператор над типами Pair, а также полиморфные

функции pair, fst и snd, принадлежащие требуемым типам.

Вот один из способов построить пакет с таким типом:

pa irADT =

{*λX. λY . R . (X ->Y -R ) -> R ,

{ pair = λX . λY . λx :X. λy : Y.

λR . λp:X ->Y -> R. p x y ,

fst = λX . λY. λp: R. (X ->Y ->R ) -> R

p [X] (λx : X. λy: Y . x ),

snd = λX . λY. λp: R. (X ->Y ->R ) -> R

p [Y] (λx : X. λy: Y . y )}} as PairSig ;

pa irADT : PairSi g

Внутренним скрытым типом представления служит оператор λX. λY. R. (X Y R) R, который

мы уже ранее использовали (§24.2) для представления пар. Компоненты pair, fst и snd в теле постро-

ены как полиморфные функции требуемых типов.

Когда АТД определен, мы можем его распаковать обычным способом:

let { Pair , pair } = pairAD T

in pair . fst [ Nat ] [ Bool ] ( pair . pair [ Nat ] [ Bool ] 5 true );

5 : Nat

30.3. Свойства исчисления

Теперь мы переходим к доказательству основных свойств F

— в частности, как обычно, теорем

о сохранении и продвижении. Идеи, лежащие в основе этих доказательств, почти такие же, как то,

что мы видели раньше, но требуется соблюдать осторожность, поскольку сейчас мы работаем с до-

вольно большой и сложной системой. В частности, потребуются заметные усилия при анализе струк-

туры отношения эквивалентности типов. Чтобы сократить доказательства, мы будем работать только

с фрагментом F

, содержащим кванторы общности, то есть, с системой, опеределенной на Рис. 30.1.

Распространение доказательств на кванторы существования не представляет большого труда.

30.3.1. Базовые свойства

Для начала мы доказываем некоторые простые свойства системы, которые понадобятся нам позднее.

Лемма 30.3.1 Усиление : Если Γ, x:S, ∆ T :: K, то Γ, ∆ T :: K.

Доказательство: В определении отношения присвоения видов нигде не упоминаются связывания тер-

мовых переменных.

Разнообразия ради, мы доказываем свойства перестановки и ослабления для F

совместно, а не по

отдельности, как мы это делали до сих пор.

rev. 104

30.3. Свойства исчисления 349

Лемма 30.3.2 Перестановка и ослабление : Допустим, у нас есть контексты Γ и ∆, причем ∆

— правильно построенная перестановка контекста Γ, Σ для некоторого Σ — то есть, ∆ является

перестановкой некоторого расширения Γ.

1. Если Γ T :: K, то ∆ T :: K.

2. Если Γ t : T, то ∆ t : T.

Доказательство: Прямолинейная индукция по деревьям вывода.

Лемма 30.3.3 Подстановка термов : Если Γ, x:S, ∆ t : T и Γ s : S, то Γ, ∆ x s t : T.

Доказательство: Индукция по деревьям вывода. (Упражнение : На каком шаге используется

Лемма 30.3.1? А Лемма 30.3.2?)

Лемма 30.3.4 Подстановка типов :

1. Если Γ, Y::J, ∆ T :: K и Γ S :: J, то Γ, Y S ∆ Y S T :: K.

2. Если T U, то Y S T Y S U.

3. Если Γ, Y::J, ∆ t : T и Γ S :: J, то Γ, Y S ∆ Y S t : Y S T.

Доказательство: Прямолинейная индукция по деревьям вывода. В вариантах K-TVar и K-Var ис-

пользуется лемма об ослаблении (Лемма 30.3.2). В варианте Q-AppAbs требуется также заме-

тить, что X Y S T

Y S T

совпадает с Y S X T

30.3.2. Эквивалентность и редукция типов

Чтобы установить свойства типизации в F

, удобно воспользоваться направленным вариантом от-

ношения эквивалентности типов, называемым параллельная редукция (Рис. 30.3). В отличие от от-

ношения эквивалентности типов, здесь отсутствуют правила симметрии и транзитивности, а правило

QR-AppAbs разрешает редукцию в составляющих редекса. Отказ от симметрии придает отношению

редукции более «вычислительный» характер, поскольку (λX::K

) T

переходит в X T

но не наоборот; при такой направленности отношение оказывается легче анализировать, например, в

доказательстве Леммы 30.3.12, далее в этом разделе. То, что мы отказываемся от транзитивности и поз-

воляем компонентам проходить редукцию одновременно с лямбда-редексом — технические детали: мы

вводим эти изменения ради того, чтобы выполнялось одношаговое свойство ромба, сформулированное

ниже в Лемме 30.3.8.

Ключевое свойство отношения параллельной редукции состоит в том, что его транзитивно-

симметричное замыкание, обозначаемое WV , совпадает с эквивалентностью типов.

Лемма 30.3.5 S T тогда и только тогда, когда S WV T.

Доказательство: В направлении ( ) утверждение очевидно. В направлении ( ) единственная слож-

ность состоит в том, что, в то время как в выводе отношения эквивалентности типов экземпля-

ры правил Q-Symm и Q-Trans могут использоваться на любом шаге, определение WV позволя-

ет использовать симметрию и транзитивность только на самом внешнем уроне. Справиться с

этой трудностью удается, если заметить, что любой вывод S T можно преобразовать в цепочку

S S

. . . S

T, так что каждый из этих выводов свободен от транзитивности,

они скрепляются транзитивностью на самом верхнем уровне, и при этом в каждом выводе S

i 1

правило Q-Symm может использоваться (если используется вообще) только на последнем шаге.

Более того, нетрудно видеть, что отношение параллельной редукции конфлюэнтно, как показывают

следующие несколько лемм. Часто конфлюэнтность называют свойством Чёрча-Россера.

Лемма 30.3.6 Если S V S , то Y S T V Y S T для любого типа T.

Доказательство: Индукция по структуре T.

rev. 104

350 30.3. Свойства исчисления

Лемма 30.3.7 Если S V S и T V T , то Y S T V Y S T .

Доказательство: Индукция по второму данному выводу. В варианте QR-Refl используется Лем-

ма 30.3.6. В вариантах QR-Abs, QR-App, QR-Arrow и QR-All достаточно применить пред-

положение индукции. В варианте QR-AppAbs имеем T (λX::K

) T

и T X T

причем T

V T

и T

V T

. Согласно предположению индукции, Y S T

V Y S T

Y S T

V Y S T

. Применяя QR-AppAbs, получаем (λX::K

. Y S T

) Y S T

V X

Y S T

, т. е., Y S (λX::K

) T

V Y S X T

Лемма 30.3.8 Одношаговое свойство ромба для редукции : Если S V T и S V U, то существу-

ет некоторый тип V, такой, что T V V и U V V.

Доказательство: Упражнение Рекомендуется, .

Лемма 30.3.9 Конфлюэнтность : Если S V T и S V U, то существует некоторый тип V, такой,

что T V V и U V V.

Доказательство: Если мы изобразим отдельные шаги редукции от S к T и от S к U следующим обра-

зом:

x



&

}w

}

'

|v

(

T U

то с помощью многократного применения Леммы 30.3.8 можно будет заполнить внутренность диа-

граммы

|v

(

yu

(

)

|v

( |v

(

zv

( zv

(

|v

(

|v

)

|v

(

yu

(

|v

и получить большой ромб. Нижние стороны этого ромба представляют собой требуемые редукции.

Утверждение 30.3.10 Если S WV T, то существует некоторый тип U, такой, что S V U и T V U.

Доказательство: Упражнение .

Это приводит нас к ключевому наблюдению о связи эквивалентности типов и редукции: если два

типа эквивалентны, через редукцию их можно привести к общей форме. Такая структура достаточна

для доказательства свойств инверсии дальше в этом разделе.

Следствие 30.3.11 Если S T, то существует некоторый тип U, такой, что S V U и T V U.

rev. 104