Пирс Б. Типы в языках программирования

Подождите немного. Документ загружается.

Глава 31

Наследование высших порядков

Последняя система, которую мы рассмотрим в этой книге, называется F

. Она, как и F

, пред-

ставляет собой сочетание характеристик, уже исследованных нами по отдельности — на этот раз это

операторы над типами и наследование. Можно рассматривать ее как расширение Системы F

, лямбда-

исчисления второго порядка с ограниченной квантификацией, при помощи операторов над типами. Са-

мая интересная новая характеристика F

— то, что отношение наследования распространяется с вида

* на типы высших видов.

В литературе было предложено несколько разновидностей F

, различающихся по выразительной

мощности и метатеоретической сложности. Та, которую мы рассматриваем здесь, очень близка к од-

ной из самых простых, версии Пирса и Стеффена (Pierce and Steﬀen 1994). Мы не будем доказывать

никакие свойства этой системы; такие доказательства можно найти у Пирса и Стеффена, либо у Компа-

ньони (Compagnoni 1994) или Абади и Карделли (Abadi and Cardelli 1996), где рассматриваются схожие

системы. (Чтобы представить, как много места занимают эти доказательства, помножьте сложности

Главы 28 на те, которые описаны в §30.3.)

Основная причина, по которой мы изучаем F

— то, что эта система служит основой нашего послед-

него расширенного примера, касающегося объектно-ориентированного программирования (Глава 32).

Этот пример не использует никаких особенных хитростей определения F

. Требуется только иметь

возможность построить ограниченную квантификацию по подтипам данного оператора над типами.

Таким образоим, читатель может при желании пропустить эту главу при первом чтении и вернуться к

ней, если возникнут вопросы.

31.1. Интуитивные понятия

Взаимодействие наследования и ограниченной квантификации с операторами над типами порож-

дает некоторые сложности при проектировании комбинированной системы. Прежде, чем приступить к

формальному определению, мы кратко обсудим эти сложности.

Первый вопрос состоит в том, следует ли при наличии наследования обобщить операторы над ти-

пами формы λX::K

до ограниченных операторов над типами формы λX<:T

. В этой главе при

выборе между простотой и регулярностью исчисления мы выбираем простоту, и в нашей системе при-

сутствует ограниченная квантификация и неограниченные операторы над типами.

Второй вопрос заключается в том, как расширить отношение наследования, включив в него опера-

торы над типами. Имеется несколько альтернатив. Простейшая из них, которую мы выбираем в этой

главе — поднять отношение наследования на простых типах на уровень операторов поточечно. Для

абстракций мы говорим, что λX.S является подтипом λX.T тогда, когда применение их обеих к типу U

всегда дает типы, находящиеся в отношении наследования. Например, λX.Top X является подтипом

λX.X Top, поскольку U Top есть подтип Top U при любом U. Эквивалентным образом можно сказать,

что λX.S является подтипом λX.T, если S будет подтипом T в случае, если мы рассмотрим тип X как

В этой главе изучается чистая Система F

(Рис. 31.1). Соответствующий интерпретатор называется fomsub. (Интер-

претатор fullfomsub включает в себя различные расширения, например, экзистенциальные типы.)

361

362 31.2. Определения

абстрактный, не делая никаких предположений о его подтипах и надтипах. Эта последняя формули-

ровка немедленно приводит к следующему правилу:

Γ, X S <: T

Γ λX.S <: λX.T

S-Abs

Обратным образом, если F и G являются операторами над типами и F <: G, то F U <: G U.

Γ F <: G

Γ F U <: G U

S-App

Заметим, что это правило срабатывает только в том случае, когда F и G применяются к одному и тому

же аргументу U. Если нам известно, что F поточечно является подтипом G, это ничего нам не говорит

о том, как эти два типа поведут себя, будучи применены к различным аргументам. (В 31.4) упомянуты

некоторые более сложные варианты F

, где этот случай принимается во внимание.)

Еще одно дополнительное правило возникает из значения, которое мы приписываем отношению

эквивалентности типов. Если S T, то S и T содержат одни и те же элементы. Однако ясно, что типы,

содержащие одни и те же элементы, являются подтипами друг друга. Отсюда происходит еще одно

правило наследования, где эквивалентность определений служит как базовый случай.

Γ S :: K Γ T :: K S T

Γ S <: T

S-Eq

После того, как наследование поднято от вида * на вид * *, можно таким же образом распространить

его и на более сложные виды. Например, если P и Q являются операторами над типами вида * * *,

то мы говорим, что P <: Q в том случае, если для любого U применение P U является подтипом Q U в

рамках вида * *.

Это определение имеет полезный побочный эффект: для высших видов отношения наследования

обладают максимальными элементами. Если мы скажем, что Top[*] Top, и определим (максимальные

элементы высших видов)

Top[K

]

def

λX::K

.Top[K

]

то с помощью несложной индукции можно показать, что Γ S <: Top[K] (при условии, что S имеет

вид K). В правилах следующего раздела мы используем этот эффект.

Переход от обыкновенных ограниченных кванторов к ограниченным кванторам высших порядков

не представляет труда. F

наследует от F

ограниченные кванторы вида X<:T

. Обобщение этой

конструкции на высшие порядки (то есть, на квантификацию по операторам над типами) не требует

никаких изменений в синтаксисе: мы просто говорим, что T

может быть любым выражением типа,

включая операторы. Неограниченные кванторы высших порядков, которые мы наследуем из F

, можно

рассматривать как сокращения для ограниченных кванторов с максимальным ограничением — т. е.,

мы считаем, что X::K

— сокращенная запись для X<:Top[K

].T

Наконец, F

наследует от F

вопрос, использовать ли более доступный вычислительно ядерный

вариант или более выразительно мощный полный вариант для правила S-All. Мы здесь выбираем

ядерный вариант; полный вариант тоже имеет смысл с семантической точки зрения, однако его метатео-

ретические свойства (даже те, которые, по аналогии с полной F

, как кажется, должны выполняться)

пока не установлены.

31.2. Определения

Правила, определяющие F

, приведены на Рис. 31.1. В определении имеется техническая деталь:

несмотря на то, что в системе есть две разновидности связывания для переменных типа (X::K в опе-

раторах типа и X<:T в кванторах), только одна из них — вторая, — может встречаться в контекстах.

Когда мы переводим связывание X::K с правой стороны знака штопора налево, в правилах K-Abs и

S-Abs, мы заменяем его на X<:Top[K].

Еще одна тонкая деталь состоит в том, что в F

исчезают правила S-Refl из F

и T-Eq из F

. Все

экземпляры старого S-Refl непосредственно следуют из S-Eq и Q-Refl, а правило T-Eq выводится

из T-Sub и S-Eq.

Упражнение 31.2.1 : Если мы определим Id λX.X и

Γ B<Top, A<:B, F<:Id

rev. 104

31.2. Определения 363

<: Top Основано на F

(30.1) и ядерной F

(26.1)

Синтаксис

t ::= термы:

x переменная

λx:T.t абстракция

t t применение

λX <:T .t абстракция типа

t [T] применение типа

v ::= значения:

λx:T.t значение-абстракция

λX <:T .t значение-абстракция типа

T ::= типы:

Top максимальный тип

X типовая переменная

T T тип функций

X <:T .T универсальный тип

λX::K.T абстракция оператора

T T применение оператора

Γ ::= контексты:

пустой контекст

Γ, x:T связывание термовой переменной

Γ, X<:T связывание типовой переменной

K ::= виды:

* вид простых типов

K K вид операторов

Вычисление t t’

(E-App1)

(E-App2)

(λ x:T

) v

x v

(E-AppAbs)

] t

]

(E-TApp)

(λX <:T

) [T

] X T

(T-TappTabs)

Присвоение видов Γ T :: K

Γ Top :: * (K-Top)

X<:T Γ Γ T :: K

Γ X :: K

(K-TVar)

Γ, X <:Top[K

] T

:: K

Γ λX::K

:: K

(K-Abs)

Γ T

:: K

Γ T

:: K

Γ T

:: K

(K-App)

Γ T

:: * Γ T

:: *

Γ T

:: *

(K-Arrow)

Γ, X<:T

::*

Γ X <:T

:: *

(K-All)

см. на след. странице. . .

Рис. 31.1. Ограниченная квантификация высших порядков (F

)

то какие из следующих утверждений о наследовании окажутся выводимыми?

Γ A <: Id B

Γ Id A <: B

Γ λX.X <: λX.Top

Γ λX. Y<X. Y <: λX. Y<Top. Y

Γ λX. Y<X. Y <: λX. Y<X. X

Γ F B <: B

Γ B <: F B

Γ F B <: F B

Γ F<:(λY.Top Y). F A <: F<:(λY.Top Y). Top B

Γ F<:(λY.Top Y). F A <: F<:(λY.Top Y). F B

Γ Top[* *] <: Top[* * *]

rev. 104

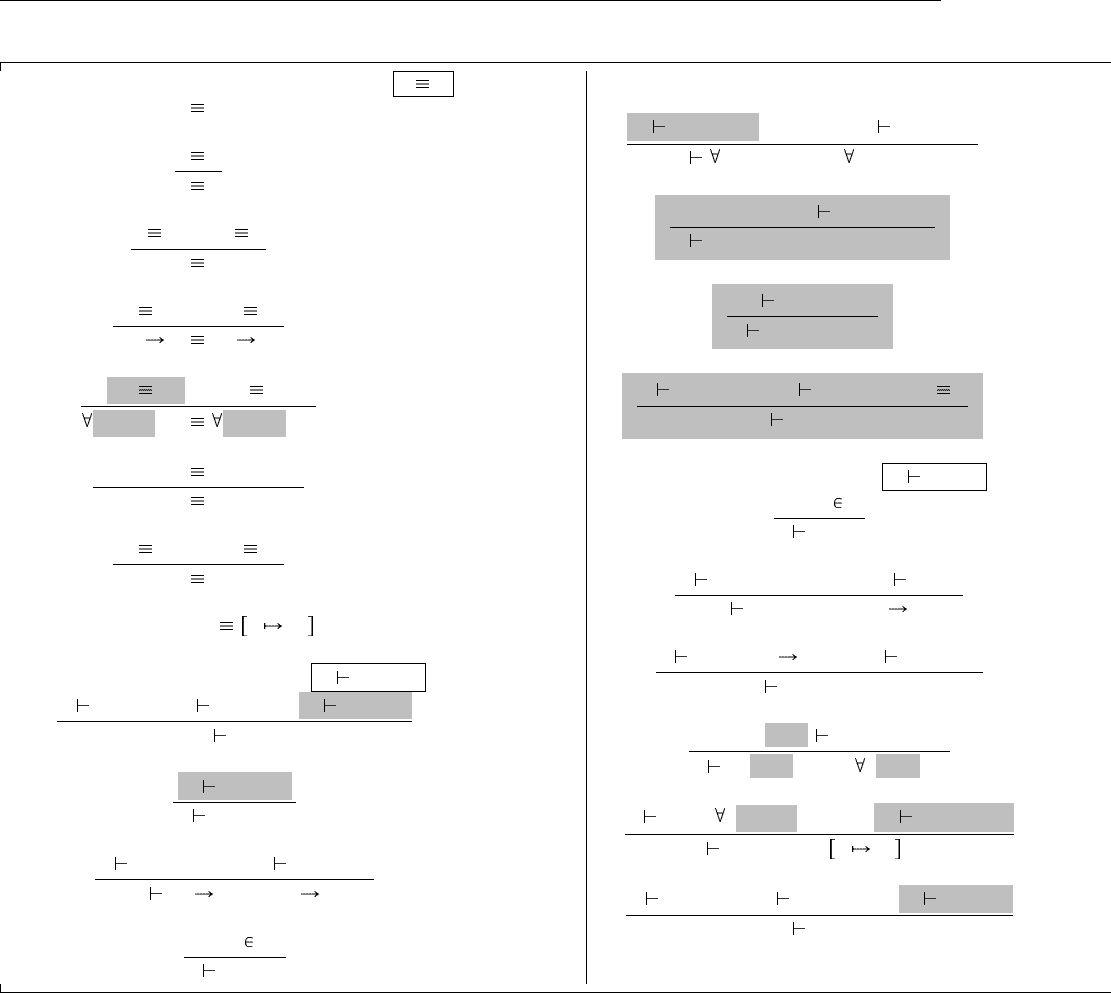
364 31.3. Свойства исчисления

Эквивалентность типов S T

T T (Q-Refl)

T S

S T

(Q-Symm)

S U U T

S T

(Q-Trans)

(Q-Arrow)

X<:S

X<:T

(Q-All)

λX::K

(Q-Abs)

(Q-App)

(λX::K

) T

X T

(Q-AppAbs)

Наследование Γ S <: T

Γ S<:U Γ U<:T Γ U :: K

Γ S<:T

(S-Trans)

Γ S :: *

Γ S <: Top

(S-Top)

Γ T

<: S

Γ S

<: T

Γ S

<: T

(S-Arrow)

X<:T Γ

Γ X <: T

(S-TVar)

Γ U

:: K

Γ, X<:U

<: T

Γ X<:U

<: X<:U

(S-All)

Γ, X<:Top[K

] S

<: T

Γ λX::K

<: λX::K

S-Abs

Γ S

<: T

Γ S

U < T

S-App

Γ S :: K Γ T :: K S T

Γ S <: T

S-Eq

Типизация Γ t : T

x : T Γ

Γ x : T

(T-Var)

Γ T

:: * Γ, x:T

Γ λx:T

: T

(T-Abs)

Γ t

: T

Γ t

: T

Γ t

: T

(T-App)

Γ, X <:T t

: T

Γ λX <:T .t

: X <:T .T

(T-TAbs)

Γ t

: X <:T

Γ T

<: T

Γ t

] : X T

X.T

(T-TApp)

Γ t : S Γ S <: T Γ T :: *

Γ t : T

(T-Sub)

Рис. 31.2. Ограниченная квантификация высших порядков (продолжение)

31.3. Свойства исчисления

Доказательства основных свойств F

, включая сохранение типов при редукции, продвижение и на-

личие минимального типа для (близкого подобия) нашей системы, можно найти в статьях, указанных в

начале данной главы. Разумеется, эти доказательства должны учитывать сложности, возникающие при

рассмотрении наследования, ограниченной квантификации и операторов над типами по отдельности.

В дополнение к этому, возникает одна существенная новая проблема, когда мы пытаемся определить

альтернативное представление правил наследования, управляемое синтаксисом: существенным образом

в комбинации с транзитивностью при выводе утверждения о наследовании может использоваться не

только правило о типовых переменных (как мы видели в §28.3), но и эквивалентность типов (правило

rev. 104

31.4. Дополнительные замечания 365

S-Eq).

Например, в контексте Γ X<:Top, F<:λY.Y утверждение Γ F X <: X можно доказать так (мы

игнорируем утверждения о видах):

Γ F <: λY.Y

S-TVar

Γ F X <: (λY.Y) X

S-App

Γ (λY.Y) X <: X

S-Eq

Γ F X <: X

S-Trans

Более того, заметим, что это взаимодействие правил нельзя обойти просто путем приведения всех выра-

жений к нормальной форме, поскольку выражение F A редексом не является — оно становится редексом

только тогда, когда в процессе проверки типов переменная F поднимается до верхней границы λY.Y.

Решение состоит в том, чтобы нормализовывать выражения типа в начале проверки наследования, а

затем, если потребуется, повторять нормализацию при каждой операции поднятия типа.

31.4. Дополнительные замечания

Многие идем F

восходят к Карделли, особенно к его статье «Структурное наследование и понятие

степенного типа» (Cardelli 1988a); расширение отношения наследования на операторы над типами было

разработано Карделли (Cardelli 1990) и Митчеллом (Mitchell 1990a). Ранняя семантическая модель

была построена Карделли и Лонго (Cardelli and Longo 1991) с использованием отношений частичной

эквивалентности. Компаньони и Пирс (Compagnoni and Pierce 1996) построили модель для расширения

типами-пересечениями. Более мощная модель, включающая рекурсивные типы, была дана Брюсом

и Митчеллом (Bruce and Mitchell 1992); родственную ей модель можно найти у Абади и Карделли

(Abadi and Cardelli 1996).

Основные метатеоретические свойства приведенного здесь варианта F

были доказаны Пирсом и

Стеффеном (Pierce and Steﬀen 1994), а также независимо от них (с использованием изящного приема

доказательства, который упрощает одно из основных рассуждений) в работе Компаньони (Compagnoni

1994). Метод Компаньони таке был использован Абади и Карделли (Abadi and Cardelli 1996) для ва-

рианта F

, использующего в качестве ядерного языка термов их исчисление объектов, а не лямбда-

исчисление.

Поточечное определение наследования между операторами над типами можно обобщить и позво-

лить наследование между применениями различных операторов к различным аргументам (F S <: G

T), если мы уточним систему видов и будем отслеживать полярность операторов над типами. Мы го-

ворим, что оператор F ковариантен, если F S <: F T всегда, когда S <: T, и контравариантен, если

F T <: F S всегда, когда S <: T. Если мы введем два новых правила наследования, отражающих эти

свойства

Γ S <: T F ковариантен

Γ F S <: F T

Γ S <: T F контравариантен

Γ F T <: F S

то по транзитивности получим F S <: G T, если F <: G, S <: T и F ковариантен. Чтобы все это ра-

ботало, нам придется отмечать полярность на типовых переменных и ограничить кванторы высших

порядков, чтобы они работали только с переменными определенных полярностей. Варианты F

с по-

лярностью рассматривались Карделли (Cardelli 1990), Стеффеном (Steﬀen 1998), а также Дагганом и

Компаньони (Duggan and Compagnoni 1999).

Еще одно возможное расширение представленной здесь F

состоит в обобщении неограниченных

операторов над типами λX::K

до ограниченных операторов над типами λX<:T

. Такой шаг

весьма привлекателен, поскольку он повторяет ход нашей мысли, когда мы переходили от неограни-

ченных к ограниченным кванторам в определении F

, при добавлении наследования в Систему F. С

другой стороны, при этом шаге система становится намного сложнее, поскольку требуется обобщить

rev. 104

366 31.4. Дополнительные замечания

также систему видов и позволить иметь виды вроде X<:T

, а это, в свою очередь, создает взаим-

ную зависимость между правилами присвоения видов и правилами наследования. Распутывние этой

зависимости требует немалой работы. См. Компаньони и Гоген (Compagnoni and Goguen 1997a; 1997b).

Расширения F

зависимыми типами исследованись Ченом и Лонго (Chen and Longo 1986), а также

Званенбургом (Zwanenburg 1999).

rev. 104

Глава 32

Расширенный пример: чисто

функциональные объекты

В последнем нашем расширенном примере мы продолжаем исследовать экзистенциальную модель

объектов. Эта модель была введена в §24.2.2, где мы показали, как можно рассматривать экзистенци-

альные пакеты в качестве простых объектов, а также сравнили характеристики этого стиля абстракции

с использованием экзистенциальных типов для реализации более привычных абстрактных типов дан-

ных. В этой главе при помощи инструментов, введенных в последней части книги (операторы над

типами и наследование высших порядков), а также новой конструкции, полиморфного обновления,

вводимого в §32.7, мы расширяем простые экзистенциальные объекты и получаем набор идиом, до-

стигающий гибкости полноценного объектно-ориентированного программирования, включая классы и

наследование.

32.1. Простые объекты

Напомним для начала тип чисто функциональных объектов-счетчиков Counter:

Co unter = { X { state :X , methods :{ get :X -> Nat , inc :X -> X }}};

Элементами этого типа являются пакеты со скрытым типом состояния X, состоянием типа X, и за-

писью, содержащей методы типа {get:X Nat,inc:X X}.

В нескольких ближайших разделах тип {x:Nat} будет служить типом представления для всех наших

объектов. (В §32.8 мы увидим, как определять объект с несколькими переменными экземпляра, а также

классы, добавляющие новые переменные экземпляра.) Говоря о внутреннем типе состояния, мы будем

использовать сокращение CounterR:

Cou nterR = {x: Nat };

Объект-счетчик — это элемент типа Counter, опеределяемый при помощи правила введения квантора

существования (T-Pack с Рис. 24.1).

c = {* CounterR ,

{ state = {x =5} ,

me thods = { get = λr: Counte rR . r .x ,

inc = λr : Cou n terR . {x = succ (r . x )}}}} as Counter ;

c : Counte r

Для вызова методов объекта типа Counter следует этот объект распаковать, выбрать нужное поле

записи методов и применить его к состоянию,

Примеры этой главы являются термами F

(Рис. 31.1) с записями (11.7), числами (8.2) и полиморфными обновле-

ниями (Рис. 32.1). Соответствующий интерпретатор на OCaml называется fullupdate.

367

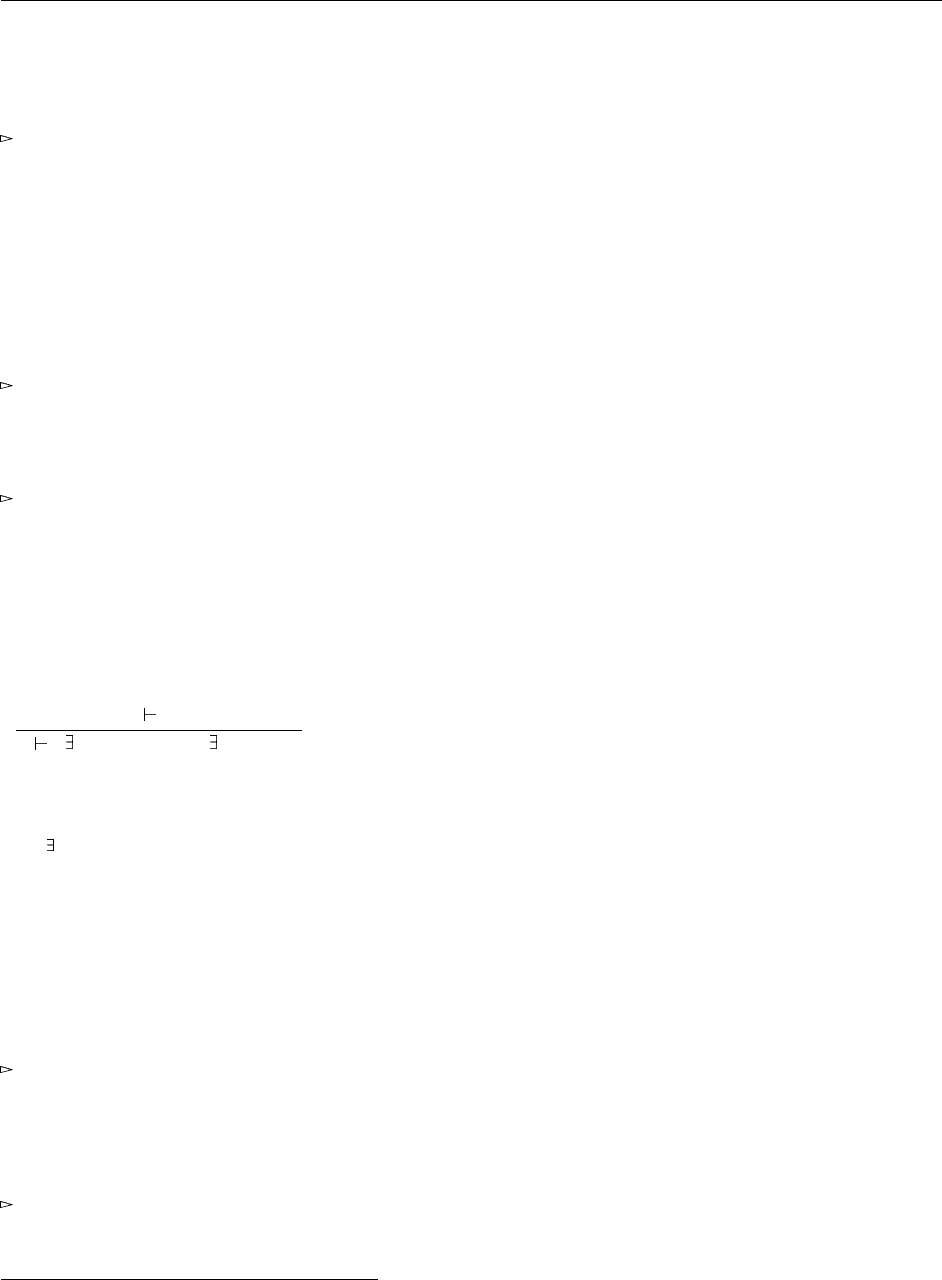
368 32.2. Наследование

se ndget = λc: Counter .

let {X , body } = c in

body . m ethods . get ( body . state );

se ndget : Counte r -> Nat

и наконец, (в случае с inc, который должен вернуть новый объект, а не просто голое число), при

необходимости результат надо перепаковать в новый объект с тем же типом представления и методами,

что и в исходном объекте.

se ndinc = λc: Counter .

let {X , body } = c in

{*X ,

{ state = body . m ethods . inc ( body . state ) ,

me thods = body . metho ds }} as Counter ;

se ndinc : Counte r -> C ounter

При помощи этих базовых функций можно строить более сложные термы, манипулирующие объектами-

счетчиками.

add three = λc: Counte r . sendinc ( sendi nc ( sendi nc c ));

add three : Counter -> Counter

32.2. Наследование

Приятное свойство такого экзистенциального кодирования объектов — то, что отношения наследо-

вания, которые мы хотим установить между типами объектов, прямо следуют из правил наследования

для кванторов существования и записей. Чтобы убедиться в этом, вспомним (с Рис. 26.3) правило на-

следования для экзистенциальных типов.

Γ, X<:U S

<: T

Γ { X<:U,S

} <: { X<:U,T

}

(S-Some)

Это правило непосредственно говорит нам, что, если мы определим тип объектов, у которого методов

больше, чем у Counter, например,

ResetCounter =

{ X , { state :X , method s :{ get : X -> Nat , inc :X - >X , reset :X ->X }}};

то он окажется подтипом Counter, т. е., ResetCounter <: Counter. А значит, если мы определим

объект-счетчик с возможностью сброса,

rc = {* CounterR ,

{ state = {x =0} ,

me thods = { get = λr: Counte rR . r .x ,

inc = λr : Cou n terR . {x = succ (r . x)} ,

reset = λr : Cou n terR . {x =0}}}} as ResetCounter ;

rc : ResetCounter

то по правилу включения мы сможем передавать этот объект в функции, определенные для типа

Counter, вроде sendget, sendinc и addthree:

rc3 = addthr ee rc ;

rc3 : Coun ter

Однако заметим, что при этом мы теряем информацию о типах: типом rc3 оказывается просто Counter,

а не ResetCounter.

Мы здесь используем только ядерный вариант правила; вся мощность полной версии нам не требуется. В сущности,

нам в этой главе вообще не нужны ограниченные экзистенциальные типы — ограничением во всех кванторах существо-

вания будет Top.

rev. 104

32.3. Ограниченная квантификация 369

32.3. Ограниченная квантификация

Разумеется, именно такого рода потеря информации из-за включения послужила причиной вве-

дения ограниченной квантификации в Главе 26. Однако ограниченная квантификация сама по себе

недостаточна — для решения стоящей перед нами сейчас проблемы ее нужно обогатить некоторым

дополнительным механизмом.

Чтобы понять, почему это так, рассмотрим очевидное уточнение типа sendinc при помощи ограни-

ченной квантификации — C<:Counter. C C. Если наш sendinc будет иметь такой тип, мы сможем

записать addthree как

add three = λC <: Counte r . λc :C.

se ndinc [C] ( send inc [C ] ( sendin c [ C ] c ));

add three : C <: Cou nter . C -> C

и, применив его к rc, получить результат типа ResetCounter.

rc3 = addthr ee [ R e s e t C o u n t e r ] rc ;

rc3 : ResetCounter

К сожалению, у нас нет способа написать такую функцию – или, точнее, нет способа написать

функцию, ведущую себя как нам надо и дать ей такой тип. Разумеется, можно написать функцию

тождества с таким типом,

wrongsendinc = λC <: Count er . λc :C . c ;

wrongsendinc : C <: Co unter . C -> C

однако если мы попытаемся улучшить настоящую реализацию sendinc, добавив в начало ограниченную

абстракцию типа, у нас получится ошибка типизации.

se ndinc =

λC <: Cou nter . λc : C.

let {X , body } = C in

{*X ,

{ state = body . m ethods . inc ( body . state ) ,

me thods = body . metho ds }}

as C ;

Ошибка: требуется экзистенциальный тип

Проблема кроется в последней строке. Аннотация as C говорит процедуре проверки типов: «используй

экзистенциальный тип C для создаваемого здесь пакета». Но C не является экзистенциальным типом —

это типовая переменная. Это не просто глупое ограничение правил типизации, как мы их определили —

например, что правила «не знают», что всякий подтип экзистенциального типа есть экзистенциальный

тип. Напротив, было бы неверно присваивать пакету

{*X ,

{ state = body . m ethods . inc ( body . state ) ,

me thods = body . metho ds }}

тип C. Заметим, например, что тип

{ X , { state :X , method s :{ get :X -> Nat , inc :X ->X} , junk : Bool }}

является подтипом Counter. Но приведенный нами пакет определенно не имеет такого типа: в нем нет

поля junk. Таким образом, неверно, что для люого подтипа Counter тело приведенного выше варианта

sendinc «на самом деле» имеет тип C, и только правила типизации этого не видят. Можно даже показать

(например, используя денотационную модель для F

— см. (Robinson and Tennent 1988)), что в чистой

типы, имеющие форму C<:T.C C, содержат только функции тождества.

Было предложено несколько способов обойти этот недостаток F

. Один из них состоит в переходе от

к F

с использованием ограниченной квантификации высших порядков для дальнейшего уточнения

rev. 104

370 32.4. Типы интерфейсов

типа функций вроде sendinc. Другая возможность — сохранить тип C<:Counter.C C, но добавить в

язык конструкции, позволяющие построить интересные элементы такого типа. Наконец, еще вариант

— просто добавить в язык ссылки. Однако этот последний путь мы уже испробовали в Главе 27; в этой

главе наша цель — посмотреть, чего можно добиться — и как, — в рамках чисто функционального

стиля.

Последующее изложение сочетает два из перечисленных методов. Для разрешения проблем с кван-

тификацией по типам объектов, замеченных нами в предыдущем разделе, используется F

, а похожие

сложности при работе с переменными экземпляра (§32.8) решаются через новую элементарную кон-

струкцию для полиморфного обновления записей (§32.7).

32.4. Типы интерфейсов

При помощи операторов над типами можно выразить Counter как комбинацию двух частей

Co unter = O bject C ounterM ;

где

Cou nterM = λR. { get : R - >Nat , inc :R -> R};

— оператор вида * *, представляющий конкретный интерфейс методов для объектов-счетчиков, а

Ob ject = λM ::* *. { X , { state :X , m ethods :M X }};

— оператор вида (* *) *, отражающий общую структуру всех объектных типов. При такой новой

формулировке мы добиваемся отделения переменной части (интерфейса методов), где хотим разрешить

наследование, от жесткого скелета объектов (упаковка в экзистенциальный тип и пара, состоящая из

состояния и методов), где наследование не нужно, поскольку мешает переупаковке.

Для того, чтобы достичь этого разделения, требуется ограниченная квантификация по операторам

над типами, поскольку таким образом нам удается вытянуть интерфейс методов из типа объектов,

несмотря на то, что в интерфейсе упоминается тип состояния X — переменная, связанная квантором

существования, — путем абстракции самого интерфейса методов по переменной X. Таким образом,

интерфейс становится «параметрическим параметром». Такая повторная параметризация отражается

как в виде Object, так и в последовательности шагов, когда упрощается применение Object CounterM:

сначала CounterM подставляется в тело Object, и получается

{ X , { state :X , method s :(λR . { get : R ->Nat , inc :R ->R }) X }}

а затем проводится подстановка X в тело CounterM, и получается

{ X , { state :X , method s :{ get :X -> Nat , inc :X -> X }}}.

Если мы таким же образом разделим ResetCounter,

ResetCounterM = λR. { get : R - >Nat , inc :R ->R , reset :R ->R };

ResetCounter = Object R e s e t C o u n t e r M ;

то получим не только

ResetCounter <: Co unter

но и

ResetCounterM <: Count erM

согласно правилам о наследовании для операторов над типами. Таким образом, разделение объектных

типов на обобщенный каркас и специализированный интерфейс дает нам осмысленное понятие насле-

дования интерфейсов, отдельное от отношений наследования между конкретными типами объектов.

Наследование интерфейсов тесно связано — как концептуально, так и технически, — с идеей соот-

ветствия, введенной Брюсом и др. (Bruce et al. 1997) и впоследствии исследованной Абади и Карделли

(Abadi and Cardelli 1995, 1996).

rev. 104